当前位置：首页 > news >正文

LeetCode算法日记 - Day 30: K 个一组翻转链表、两数之和

news 2025/9/3 16:02:26

1. K 个一组翻转链表

1.1 题目解析

1.2 解法

1.3 代码实现

2. 两数之和

2.1 题目解析

2.2 解法

2.3 代码实现

1. K 个一组翻转链表

25. K 个一组翻转链表 - 力扣（LeetCode）

给你链表的头节点 head ，每 k 个节点一组进行翻转，请你返回修改后的链表。

k 是一个正整数，它的值小于或等于链表的长度。如果节点总数不是 k 的整数倍，那么请将最后剩余的节点保持原有顺序。

你不能只是单纯的改变节点内部的值，而是需要实际进行节点交换。

示例 1：

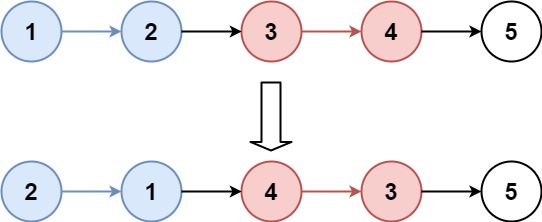
输入：head = [1,2,3,4,5], k = 2
输出：[2,1,4,3,5]

示例 2：

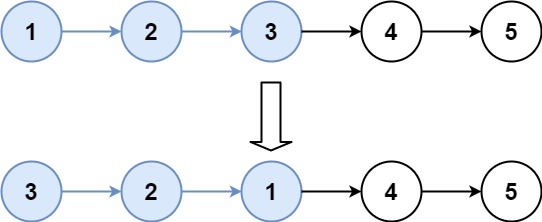
输入：head = [1,2,3,4,5], k = 3
输出：[3,2,1,4,5]

提示：

链表中的节点数目为 n
1 <= k <= n <= 5000
0 <= Node.val <= 1000

1.1 题目解析

题目本质
这是一个“分段原地翻转”的链表题：把链表按长度为 k 的小段切开——每段内部反转，段与段之间正确接回。不足 k 的尾巴保持原样。

常规解法
最直观的做法：
i）先数长度 n，只处理 n / k 个完整分段；
ii）每段用“头插法”/原地反转 k 次；
iii）把反转好的这段接回前后两端；
iiii）指针前移，处理下一段。

问题分析
难点不在“如何反转 k 个节点”，而在连边与指针推进：

反转会把这段内部 next 全改掉，导致与原链表左右两侧都断开；
每段结束都需要接回两条边：
- 左：上一段的尾 → 本段新头；
- 右：本段新尾（原头） → 下一段起点；
忘任意一条都会出错（尤其是“右边那条”会丢尾巴）。

复杂度预期：每个节点最多被访问/重连常数次，时间 O(n)，空间 O(1)。

思路转折
为保证连接有序与时间 O(n)：

设立两个“钩子”指针：
- dummyPrev 始终指向已处理前缀的最末尾（上一段的新尾）；
- start 指向当前段的原头，反转后变成新尾；
段内反转结束后，必须连两条边：
- dummyPrev.next = prev（左边）
- start.next = curr（右边）
再把钩子前移：dummyPrev = start; start = curr;
这样每段都“自洽”，最后自然正确。

1.2 解法

算法思想
对每个完整的长度为 k 的小段，进行原地反转；反转后把这段用两条边接回到大链表，再把“钩子”指针移到新位置开始下一段。
段内反转核心递推（头插法）：

next = curr.next
curr.next = prev
prev = curr
curr = next

i）一次遍历统计长度 n，计算完整段数 count = n / k；

ii）设置哑节点 dummy 方便返回，初始化：

dummyPrev = dummy（上一段尾的“左钩子”）
start = head（当前段原头，“右钩子”）

iii）循环 count 次处理每段：

段内反转：从 start 开始，做 k 次“头插法”；
- 结束时：prev=本段新头，start=本段新尾，curr=下一段起点；
段间连边（两条）：
- dummyPrev.next = prev（上一段尾 → 本段新头）
- start.next = curr（本段新尾 → 下一段头）
钩子前移：dummyPrev = start; start = curr

iiii）返回 dummy.next。

小技巧：k <= 1 或 count == 0 可直接返回 head。

易错点

忘记右边那条边：start.next = curr，会导致尾巴丢失（尤其最后一段）。
处理完一段后推进“钩子”：dummyPrev = start; start = curr。
把 dummyPrev 和 start 当成同一角色（它们在段结尾短暂相等，但职责不同：dummyPrev 负责左连，start 负责右连）。

1.3 代码实现

/*** Definition for singly-linked list.* public class ListNode {*     int val;*     ListNode next;*     ListNode() {}*     ListNode(int val) { this.val = val; }*     ListNode(int val, ListNode next) { this.val = val; this.next = next; }* }*/
class Solution {public ListNode reverseKGroup(ListNode head, int k) {if (head == null || k <= 1) return head; // 边界：k=1 或空链表无需处理// 1) 统计长度，确定完整分组数int n = 0;ListNode curr = head;while (curr != null) {n++;curr = curr.next;}int count = n / k;if (count == 0) return head; // 不足一组，直接返回// 2) 准备哑节点与“钩子”指针ListNode dummy = new ListNode(0);dummy.next = head;               // 哑节点用于返回结果ListNode dummyPrev = dummy;      // 左钩子：已处理前缀的尾ListNode start = head;           // 右钩子：当前分组原头（反转后成为新尾）// 3) 逐组处理for (int i = 0; i < count; i++) {// 3.1 段内反转 k 次ListNode prev = null;curr = start; // 从本组原头开始反转for (int j = 0; j < k; j++) {ListNode next = curr.next;curr.next = prev;prev = curr;curr = next; // 正确推进到未反转部分}// 此时：prev=本组新头，start=本组新尾（原头），curr=下一段起点// 3.2 段间连边（两条都要！）dummyPrev.next = prev; // 左边：上一段尾 -> 本组新头start.next = curr;     // 右边：本组新尾(原start) -> 下一段起点// 3.3 钩子前移，开始下一组dummyPrev = start; // 新尾成为已处理前缀的尾start = curr;      // 下一组原头}// 4) 返回结果return dummy.next;}
}

复杂度分析

时间复杂度：O(n)，每个节点被常数次访问/重连。
空间复杂度：O(1)，只用到若干指针。

2. 两数之和

1. 两数之和 - 力扣（LeetCode）

给定一个整数数组 nums 和一个整数目标值 target，请你在该数组中找出 和为目标值 target 的那两个整数，并返回它们的数组下标。

你可以假设每种输入只会对应一个答案，并且你不能使用两次相同的元素。

你可以按任意顺序返回答案。

示例 1：

输入：nums = [2,7,11,15], target = 9
输出：[0,1]
解释：因为 nums[0] + nums[1] == 9 ，返回 [0, 1] 。

示例 2：

输入：nums = [3,2,4], target = 6
输出：[1,2]

示例 3：

输入：nums = [3,3], target = 6
输出：[0,1]

提示：

2 <= nums.length <= 104
-109 <= nums[i] <= 109
-109 <= target <= 109
只会存在一个有效答案

2.1 题目解析

题目本质
把“找两数和为 target”的问题，转成“对当前数 x，另一个数要等于 need = target - x；只要我能在 O(1) 时间判断 need 是否已出现，就能立即返回答案”，如果查询不到则设为 -1 充当哨兵值，只需要判断哨兵值就可以知道哈希表吃否存在 need。这就是补数查找。

常规解法
双重循环暴力：枚举每对 (i,j)，检查 nums[i] + nums[j] == target，返回 [i,j]。

问题分析
暴力解时间 O(n^2)；当 n 接近 1e4 时，就不够优雅。并且做了大量重复比较。

思路转折
用哈希表记录“值 → 索引”。一边遍历一边查补数：
遍历到 i 时，先算 need = target - nums[i]：

如果 need 已经在表里，直接返回 [idx(need), i]；
否则把当前数 nums[i] 的“值→索引”存进表，继续。
这样每个元素只出表一次，时间 O(n)、空间 O(n)。
小建议：先查再放，避免把自己配给自己（“不能使用两次相同的元素”）。

2.2 解法

算法思想
单遍扫描 + 哈希：

need=target−nums[i], if need∈map⇒return [map[need],i]

否则 map[nums[i]] = i 继续。

i）创建 Map<Integer,Integer> map，表示“值 → 索引”。

ii）从左到右遍历 i：

计算 need = target - nums[i]；
若 map 中存在 need，返回 [map.get(need), i]；
否则 map.put(nums[i], i)。

iii）按题意“必有解”，理论上不会走到返回空数组。

易错点

返回值而不是索引（容易错）。
先 put 再查会把自己配给自己（违背“不用两次相同元素”）。应先查后放。
用 getOrDefault(tmp, 0) 判断存在性会误判：索引 0 合法。若用哨兵，选 -1；
极端数据溢出：比较时用 need = target - nums[i]（已避免溢出加法）
有重复值时，哈希中应保存最早出现的那个索引吗？一遍扫天然满足：先遇到的先放，后遇到的与之匹配直接返回即可。

2.3 代码实现

import java.util.HashMap;
import java.util.Map;class Solution {public int[] twoSum(int[] nums, int target) {Map<Integer,Integer> hash = new HashMap<>();for (int i = 0; i < nums.length; i++) {int need = target - nums[i];int j = hash.getOrDefault(need, -1); // -1 不与合法索引冲突if (j != -1) return new int[]{j, i};hash.put(nums[i], i);}return new int[0];}
}

复杂度分析