算法 --- 模拟

模拟
模拟算法的题目类型就是“流程再现型”,它适用于那些题目描述已经包含了清晰、完整的操作步骤或规则,你只需要严格按照这些步骤用代码重现一遍过程即可得到答案的题目。
详细说明:
1. 核心特征:题目类型是什么?
模拟题没有特定的算法套路,它本身就是一个大类。这类题目的共同点是:
-
过程清晰:题目会详细描述一个事件、一个系统或一个游戏的运行规则和步骤。
-
按部就班:解题思路非常直接,就是“翻译”题目描述。你不需要奇妙的数学公式或复杂的算法优化(有时需要),关键是准确无误地遵循既定规则来实现代码。
-
考察基本功:它纯粹考察你的代码实现能力、逻辑严谨性、边界条件处理以及对数据结构(如数组、字符串、队列、栈等)的熟练运用。
常见的具体形式包括:
-
行为模拟:模拟一个对象的移动(如机器人、蛇、贪吃蛇)、游戏过程(如棋牌类、桌上游戏)。
-
时间序列模拟:模拟一个时间线内发生的事件,如处理排队、调度任务。
-
系统流程模拟:模拟一个真实系统的运作,如操作系统中的页面置换算法、银行家算法。
-
语法分析模拟:模拟编译器的部分工作,如计算器、表达式求值。
2. 什么题目适用于模拟?
判断一道题是否适合用模拟算法,就问自己一个问题:“我能不能几乎不经过深度思考,只是像一台机器一样,完全按照题目说的第一步、第二步、第三步……去操作,就能得到最终结果?”
如果答案是“能”,那么它就是一道模拟题。
非常适合用模拟算法解决的题目通常具有以下特点:
-
题目描述冗长:往往有很长的背景故事和规则说明。
-
输入输出明确:输入是什么,输出是什么,非常清楚。
-
步骤化:解决问题的过程可以被分解成一系列清晰的、顺序的或循环的步骤。
-
逻辑简单但繁琐:每一步的操作可能很简单(比如判断方向、加减数字、比较大小),但组合起来步骤很多,容易出错。
举个经典例子:
-
题目:约瑟夫环问题(描述略)。
-
为什么适用模拟:规则极其清晰——“一群人围成一圈,从第一个人开始报数,数到某个数的人出列,下一个人重新从1开始报数,直到所有人都出列”。你完全可以用一个数组(或链表)模拟这些人,用一个指针模拟当前报数的人,用一个计数器模拟当前报的数,然后严格按照规则进行“遍历-判断-淘汰”的循环即可。这就是最直接的模拟解法。
3. 注意事项(模拟题的陷阱)
虽然模拟的思路直接,但很容易在实现时“踩坑”:
-
边界条件:比如数组是否越界、索引何时取模、循环的终止条件是什么。
-
性能问题:有时数据规模很大,最朴素的模拟方法(如用链表每淘汰一个就删除一个节点)可能会超时。此时需要思考优化,但解题的核心思路依然是模拟,只是用了更高效的数据结构(如循环队列)或加入一些数学计算来减少不必要的步骤。
-
细节错误:对题目规则理解有偏差或代码实现时粗心,比如“数到3淘汰”和“第3个人淘汰”是不同的概念。
总结:
当你拿到一道题,发现它的解决方案就是其自身规则的代码复现时,就果断采用模拟算法。你的主要工作将是仔细阅读、准确理解和严密编码,而不是寻找一个巧妙的算法捷径。
题目练习
1576. 替换所有的问号 - 力扣(LeetCode)
解法(模拟):
算法思路:
纯模拟。 从前往后遍历整个字符串,找到问号之后,就用 a ~ z 的每一个字符去尝试替换即可。
495. 提莫攻击 - 力扣(LeetCode)
解法(模拟 + 分情况讨论):
算法思路:
模拟 + 分情况讨论。
计算相邻两个时间点的差值:
i. 如果差值大于等于中毒时间,说明上次中毒可以持续 duration 秒;
ii. 如果差值小于中毒时间,那么上次的中毒只能持续两者的差值。
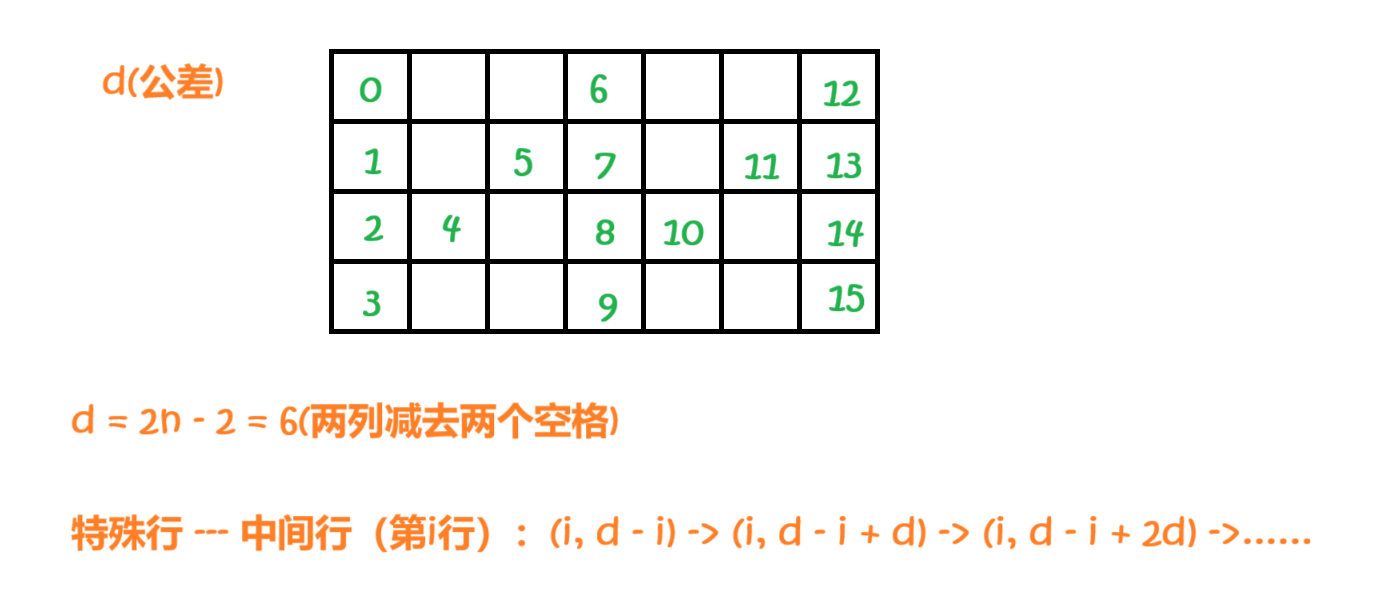
6. Z 字形变换 - 力扣(LeetCode)
注意:我们对模拟题目的优化基本都是找规律!
解法(模拟 + 找规律):
算法思路:
找规律,用 row 代替行数,row = 4 时画出的 N 字形如下:
0 2row-2 4row-41 2row-3 2row-1 4row-5 4row-32 2row-4 2row 4row-6 4row-23 2row+1 4row-1不难发现,数据是以 2row - 2 为一个周期进行规律变换的。将所有数替换成用周期来表示的变量:
-
第一行的数是:0, 2row - 2, 4row - 4;
-
第二行的数是:1, (2row - 2) - 1, (2row - 2) + 1, (4row - 4) - 1, (4row - 4) + 1;
-
第三行的数是:2, (2row - 2) - 2, (2row - 2) + 2, (4row - 4) - 2, (4row - 4) + 2;
-
第四行的数是:3, (2row - 2) + 3, (4row - 4) + 3。
可以观察到,第一行、第四行为 2row - 2 的等差数列;第二行、第三行除了第一个数取值为行数,每组下标为 (2n - 1, 2n) 的数围绕 (2row - 2) 的倍数左右取值。
以此规律,我们可以写出迭代算法。
38. 外观数列 - 力扣(LeetCode)
解法(模拟):
算法思路:
所谓「外观数列」,其实只是依次统计字符串中连续且相同的字符的个数。依照题意,依次模拟即可。
这题模拟的过程就是使用双指针 --- 滑动窗口
1419. 数青蛙 - 力扣(LeetCode)(好好做)
解法(模拟 + 分情况讨论 + "哈希表")
算法思路:
模拟青蛙的叫声。
-
当遇到 'r' 'o' 'a' 'k' 这四个字符的时候,我们要去看看每一个字符对应的前驱字符,有没有青蛙叫出来。如果有青蛙叫出来,那就让这个青蛙接下来喊出来这个字符;如果没有,直接返回 -1;
-
当遇到 'c' 这个字符的时候,我们去看看 'k' 这个字符有没有青蛙叫出来。如果有,就让这个青蛙继续去喊 'c' 这个字符;如果没有的话,就重新搞一个青蛙。
使用哈希表,通过前驱来进行记录,k上有青蛙就搬k上的!
class Solution {
public:int minNumberOfFrogs(string croakOfFrogs) {string t = "croak";int n = t.size();vector<int> hash(n);unordered_map<char, int> index;for(int i = 0; i < n; ++i) index[t[i]] = i;for(auto ch : croakOfFrogs){if(ch == 'c'){if(hash[n - 1]) hash[n - 1]--;hash[0]++;}else{int i = index[ch];if(hash[i - 1] == 0) return -1;hash[i - 1]--;hash[i]++;}}for(int i = 0; i < n - 1; ++i){if(hash[i]) return -1;}return hash[n - 1];}
};