PINN物理信息神经网络用于求解二阶常微分方程（ODE）的边值问题，Matlab实现

代码实现了一个物理信息神经网络（Physics-Informed Neural Network, PINN），用于求解如下二阶常微分方程（ODE）的边值问题：

📌 一、主要功能

🔗 二、逻辑关联

三个文件之间的调用关系如下：

main.m → modelLoss.m → computeDerivatives.m

• main.m：主训练脚本，定义网络结构、训练循环、测试与可视化；
• modelLoss.m：计算总损失（边界条件损失 + PDE 残差损失）；
• computeDerivatives.m：使用自动微分计算网络输出的二阶导数。

🧠 三、算法步骤

1. 生成训练数据：在区间 ([0, \pi/2]) 内生成内部点和边界点；
2. 构建神经网络：3层隐藏层，每层20个神经元，使用 tanh 激活函数；
3. 训练循环：
   • 使用 dlfeval 和 modelLoss 计算损失和梯度；
   • 使用 Adam 优化器更新网络参数；
4. 测试与评估：在测试集上预测并比较解析解，绘制误差和损失曲线。

🛠 四、技术路线

• 深度学习框架：使用 MATLAB 的 dlnetwork 和自动微分（dlgradient）；
• 物理信息嵌入：将 PDE 残差作为损失项，强制网络满足物理规律；
• 自动微分：计算网络输出的二阶导数，用于构建 PDE 残差项；
• 优化算法：使用 Adam 优化器进行训练。

📐 五、公式原理

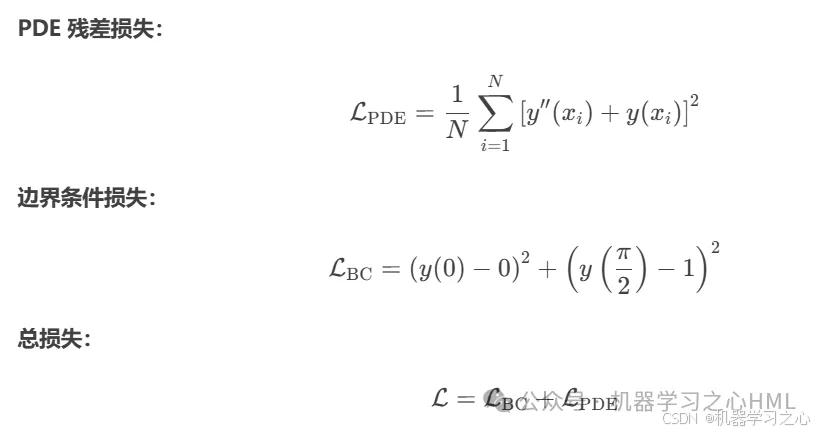
⚙️ 六、参数设定

💻 七、运行环境

• 软件：MATLAB（推荐 R2021a 或更高版本）；
• 工具箱：Deep Learning Toolbox；
• 硬件：支持 CPU 或 GPU 训练（若可用）。

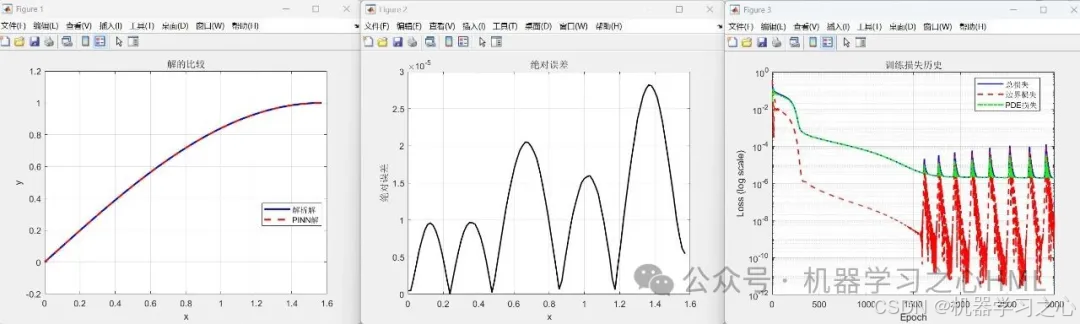
📊 输出结果

• 解的对比图（解析解 vs PINN 预测）；
• 绝对误差图；
• 训练损失曲线（总损失、边界损失、PDE 损失）；
• 最大绝对误差数值输出。

 部分源码.lineNode {font-size: 10pt; font-family: Menlo, Monaco, Consolas, "Courier New", monospace; font-style: normal; font-weight: normal; }
%% 清空环境变量
warning off             % 关闭报警信息
close all               % 关闭开启的图窗
clear                   % 清空变量
clc                     % 清空命令行
x; } .lineNode {font-size: 10pt; font-family: Menlo, Monaco, Consolas, "Courier New", monospace; font-style: normal; font-weight: normal; }
% 生成训练数据
N_interior = 100;         % 内部点数量
x_interior = linspace(xmin, xmax, N_interior)';
x_boundary = [xmin; xmax]; % 边界点
% 转换为dlarray (通道×批次格式)
x_interior_dl = dlarray(x_interior', 'CB');  % 1×100
x_boundary_dl = dlarray(x_boundary', 'CB');  % 1×2

完整源码私信回复PINN物理信息神经网络用于求解二阶常微分方程（ODE）的边值问题，Matlab实现