C++算法学习:位运算
在前面C语言的部分中,我们已经学习并了解了位置运算的相关内容。这里贴出作者之前学习的内容:C语言学习之操作符-CSDN博客
想详细了解的可以参考以上这篇代码。
而接下来我们将就位运算的思想来进行算法练习
相关算法代码已经上传至作者的个人gitee中CPP 学习代码库: C++代码库新库,旧有C++仓库满员了,喜欢请支持一下谢谢。
目录
基础位运算
位运算
位运算的应用场景
位运算的优化技巧
位运算练习题
1、对于一个数n,请确定它的二进制表示中第x位是0还是1?
2、对于一个数n,请将它的二进制表示中第x位修改为1
3、对于一个数n,请将它的二进制表示中第x位修改为0
4、位图的思想
5、提取一个数n的二进制表示中最右侧的1(lowbit)
6、干掉一个数n的二进制表示中最右侧的1
7、异或运算
1、位1的个数
2、比特位计数
3、汉明距离
1、算法一:位运算
2、算法二:__builtin_popcount函数
扩充知识:__builtin_popcount函数
一、__builtin_popcount 是什么?
4、只出现一次的数字
5、只出现一次的数字3
算法一:哈希表
算法二:位运算
6、判断字符是否唯一
算法一:哈希表
算法二:位图
7、丢失的数字
算法一:哈希表
算法二:排序
算法三:位运算
8、两整数之和编辑
9、只出现一次的数字2
算法一:哈希表
算法二:位运算
10、消失的两个数字
基础位运算
位运算
首先我们在这里简单复习一下位运算操作符
-
按位与(AND)
&(有0就是0)- 规则:两个相应位都为1时,结果为1,否则为0
- 示例:
5 & 3→0101 & 0011 = 0001(即1)
-
按位或(OR)
| (有1就是1)- 规则:两个相应位至少有一个为1时,结果为1
- 示例:
5 | 3→0101 | 0011 = 0111(即7)
-
按位异或(XOR)
^ (相同为0,相异为1)- 规则:两个相应位不同时结果为1,相同时为0
- 示例:
5 ^ 3→0101 ^ 0011 = 0110(即6)
-
按位取反(NOT)
~- 规则:对每一位取反
- 示例:
~5→~0101 = 1010(在32位系统中为-6,因为最高位是符号位)
-
左移
<<- 规则:将二进制位向左移动指定位数,低位补0
- 示例:
5 << 1→0101 << 1 = 1010(即10)
-
右移
>>- 规则:将二进制位向右移动指定位数,高位补符号位(算术右移)或补0(逻辑右移,取决于语言)
- 示例:
5 >> 1→0101 >> 1 = 0010(即2)
位运算的应用场景
-
快速乘除法
- 左移1位相当于乘以2:
x << 1=x * 2 - 右移1位相当于除以2:
x >> 1=x / 2
- 左移1位相当于乘以2:
-
判断奇偶性
x & 1 == 1→ 奇数x & 1 == 0→ 偶数
-
交换两个数
- 不使用临时变量:
a ^= b; b ^= a; a ^= b
- 不使用临时变量:
-
取反符号
~x + 1→-x
-
求绝对值
- 对于32位整数:
(x ^ (x >> 31)) - (x >> 31)
- 对于32位整数:
-
位掩码
- 设置标志位:
flags |= MASK - 清除标志位:
flags &= ~MASK - 检查标志位:
(flags & MASK) == MASK
- 设置标志位:
-
位图算法
- 用于大数据量的快速查找和去重
-
加密算法
- 如AES、DES等加密算法中大量使用位运算
位运算的优化技巧
-
n & (n-1)
- 将最低位的1变为0
- 可用于判断是否是2的幂:
(n & (n-1)) == 0
-
n & -n
- 获取最低位的1
- 可用于树状数组的实现
-
异或性质
x ^ x = 0x ^ 0 = xx ^ y ^ y = x
-
位运算优先级
- 位运算的优先级通常低于算术运算符,但高于比较运算符,建议使用括号明确运算顺序
位运算练习题
1、对于一个数n,请确定它的二进制表示中第x位是0还是1?
将n右移x位置,与上1。如果为0 则为0;如果为1则为1
思路表示,不作为最终实现代码:
(n>>x)&1;2、对于一个数n,请将它的二进制表示中第x位修改为1
将1左移x位,与n或计算
思路表示,不作为最终实现代码:
n!=(1<<x);3、对于一个数n,请将它的二进制表示中第x位修改为0
将1左移x位,与n与运算
思路表示,不作为最终实现代码:
n&=(~(1<<x));4、位图的思想
位图本质上就是哈希表(数组)
利用哈希表来存储数据来查找,现在用比特位来存储
5、提取一个数n的二进制表示中最右侧的1(lowbit)
n与上一个-n
假设n为01010001
则-n为10101111
n&(~n)6、干掉一个数n的二进制表示中最右侧的1
n与上n-1
假设n为01010001
则n-1为01010000
n&(n-1)7、异或运算
a^0=a//
a^a=0//消消乐
a^b^c=a^(b^c)
接下来是力扣算法题
1、位1的个数
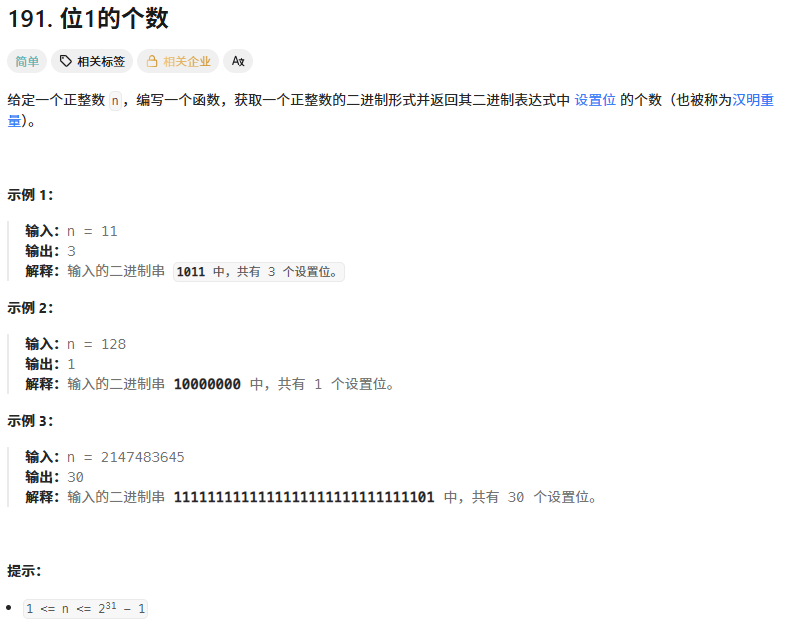
class Solution {
public:int hammingWeight(int n) {int sum=0;while(n){n&=(n-1);sum++;}return sum;}
};2、比特位计数

class Solution {
public:vector<int> countBits(int n) {vector<int>ret(n+1,0);for(int i=1;i<=n;i++){if(i&1){ret[i]=ret[i-1]+1;}else ret[i]=ret[i>>1];} return ret; }
};3、汉明距离

1、算法一:位运算
算法思路:
-
异或操作:首先,通过
x ^ y得到一个整数s,其中s的二进制表示中,每一位为1的位置表示x和y在该位不同,为0表示相同。因此,s中1的个数就是汉明距离。 -
统计1的个数:然后,通过循环检查
s的每一位,统计其中1的个数。具体做法是:-
每次检查
s的最低位(通过s & 1),如果最低位是1,则计数器ret加1。 -
然后将
s右移一位(相当于除以2),处理下一个位。
-
-
循环终止:当
s变为0时,循环结束,此时ret就是汉明距离class Solution { public:int hammingDistance(int x, int y) {// 使用异或操作:x ^ y 的结果中,每一位为1表示x和y在该位不同int s = x ^ y;int ret = 0; // 初始化结果变量,用于计数1的个数// 循环直到s变为0while (s) {// 检查s的最低位是否为1:如果为1,则s & 1的结果为1,否则为0ret += s & 1;// 将s右移一位,相当于除以2,处理下一个位s >>= 1;}return ret; // 返回汉明距离} };
2、算法二:__builtin_popcount函数
class Solution {
public:int hammingDistance(int x, int y) {return __builtin_popcount(x ^ y); }
};扩充知识:__builtin_popcount函数
一、__builtin_popcount 是什么?
__builtin_popcount 是 GCC 和 Clang 编译器提供的一个内建函数(Intrinsic Function)。
-
功能:它的作用是计算一个整数(
unsigned int)的二进制表示中1的个数。 -
词源:
popcount是 "population count"(种群计数)的缩写,这是一个从计算机体系结构领域继承来的术语,意为计算一组位中“被设置”(为1)的位的数量。 -
头文件:不需要包含任何头文件,因为它是编译器直接支持的內建函数。
基本用法:
unsigned int x = 15; // 二进制: 1111
int count = __builtin_popcount(x); // count = 4unsigned long long y = 255; // 二进制: 1111 1111
int count_y = __builtin_popcountll(y); // count_y = 8,注意使用`ll`后缀处理long long类型经典应用场景:
-
位图(Bitmap)与集合操作:
如果你用一个整数的每一位代表一个元素是否存在(例如,int的32位可以表示一个包含32个元素的集合),popcount就能瞬间告诉你这个集合中有多少个元素。 -
汉明重量(Hamming Weight):
在信息论和编码理论中,一个二进制串中1的个数被称为它的汉明重量。popcount就是计算汉明重量的操作。 -
算法题目:
-
判断一个数是否是2的幂:除了用
n & (n-1) == 0,也可以用__builtin_popcount(n) == 1。 -
子集枚举:在状态压缩DP或用位运算表示集合时,经常需要知道某个状态(一个整数)里包含了几个元素。
-
二进制表示相关的问题:比如 LeetCode 191. 位1的个数,这道题本身就是要求实现
popcount。
-
| 特性 | __builtin_popcount | 自己写的循环逐位检查 |
|---|---|---|
| 本质 | 编译器內建函数,最终编译为一条CPU指令 (POPCNT) | 一段需要循环和条件判断的C++代码 |
| 速度 | 极快 (1个时钟周期) | 慢 (需要循环n次,n是位数) |
| 可移植性 | 较好 (GCC, Clang, ICC 都支持) | 最好 (任何编译器都能编译) |
| 易用性 | 简单,一个函数调用 | 需要自己实现,容易出错 |
| 推荐使用场景 | 算法竞赛、高性能计算、位操作密集代码 | 对编译器特性有严格限制的环境 |
4、只出现一次的数字

class Solution {
public:int singleNumber(vector<int>& nums) {int x=0;for(auto s:nums){x^=s;//按位异或。//相异为1,相同为0}return x;}
};5、只出现一次的数字3

算法一:哈希表
class Solution {
public:vector<int> singleNumber(vector<int>& nums) {//哈希表unordered_map<int,int>hash;for(int x:nums){hash[x]++;} vector<int>ret;for(auto&[a,b]:hash){if(b==1){ret.push_back(a);}}return ret;}
};算法二:位运算
思路分析
-
计算异或和:首先,遍历数组计算所有元素的异或和
xorsum。由于出现两次的数字异或后会抵消为0,所以xorsum实际上是两个只出现一次的数字的异或结果。 -
找到最低位的1:然后,找到
xorsum中最低位的1(记为lsb),这一位表示两个目标数字在该位上不同(一个为0,一个为1)。这里使用xorsum & (-xorsum)来获取最低位的1,但需要处理xorsum为INT_MIN时的溢出情况。 -
分组异或:根据
lsb将数组分成两组:一组是该位为1的数字,另一组是该位为0的数字。这样两个目标数字会被分到不同组中。分别对两组进行异或操作,由于每组中其他数字都出现两次,异或后会抵消,最终得到两个目标数字。class Solution { public:vector<int> singleNumber(vector<int>& nums) {//位运算int xorsum = 0;for (int num: nums) {xorsum ^= num;}// 防止溢出int lsb = (xorsum == INT_MIN ? xorsum : xorsum & (-xorsum));int type1 = 0, type2 = 0;for (int num: nums) {if (num & lsb) {type1 ^= num;}else {type2 ^= num;}}return {type1, type2};} };
6、判断字符是否唯一

算法一:哈希表
class Solution {
public:bool isUnique(string astr) {//哈希表unordered_map<int,int>hash; for(auto& x:astr){hash[x]++; } for(auto& [a,b]:hash){if(b>1) return false;}return true;}
};算法二:位图
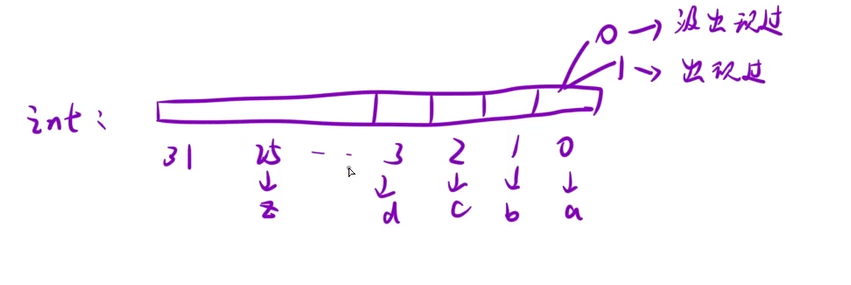
class Solution {
public:bool isUnique(string astr) {//位图//鸽巢原理优化if(astr.size()>26) return false;int bitmap=0;for(auto& x:astr){int i=x-'a';//判断字符是否在哈希表中if(((bitmap>>i)&1)==1) return false;//把当前字符填入位图bitmap|=1<<i;}return true;}
};7、丢失的数字

算法一:哈希表
class Solution {
public:int missingNumber(vector<int>& nums) {//哈希表unordered_map<int,int>hash;for(auto& x:nums){hash[x]=1;}for(int i = 0; i <= nums.size(); i++){if(!hash[i]){return i;}}return 0; }
};算法二:排序
class Solution {
public:int missingNumber(vector<int>& nums) {//排序int n=nums.size();sort(nums.begin(),nums.end());for(int i=0;i<n;i++){if(nums[i]!=i)return i;} return n;}
};算法三:位运算
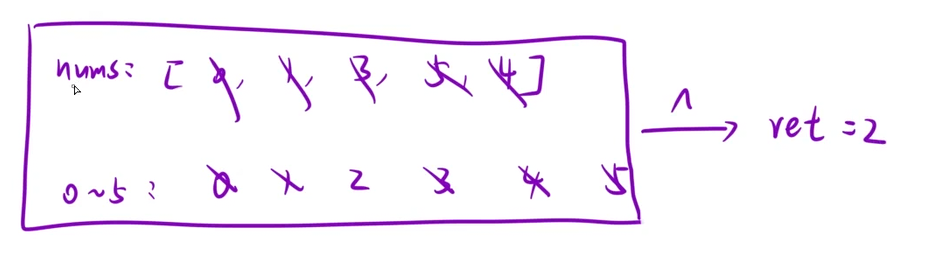
class Solution {
public:int missingNumber(vector<int>& nums) {//位运算int ret=0;for(auto& x:nums) ret^=x;for(int i=0;i<nums.size();i++) ret^=i;return ret;}
};8、两整数之和
算法思想:异或运算-无进位相加
class Solution {
public:int getSum(int a, int b) {while (b != 0) // 当进位不为0时继续循环{ int x = a ^ b; // 计算不考虑进位的和unsigned int carry = (unsigned int)(a & b) << 1; // 计算进位。转为无符号防止有符号左移的未定义行为a = x;b = carry; // 将进位赋值给b,进入下一轮循环}return a; }
};9、只出现一次的数字2

算法一:哈希表
class Solution {
public:int singleNumber(vector<int>& nums) {//哈希表unordered_map<int,int>hash;for(auto& x:nums){hash[x]++;} for(auto& [a,b]:hash){if(b==1) return a;}return 0;}
};算法二:位运算
class Solution {
public:int singleNumber(vector<int>& nums) {//位运算int ret=0;for(int i=0;i<32;i++)//依次修改每一位{int sum=0;for(int x:nums )//计算nums中所有数第i位的和{if((x>>i)&1==1){sum++;}}sum%=3;if(sum==1){ret|=1<<i;}}return ret;}
};10、消失的两个数字

算法思路:
1、将所有的数字异或在一起,存储为tmp。
2、找到tmp上比特位为1的那个
3、根据x位不同划分为两类异或
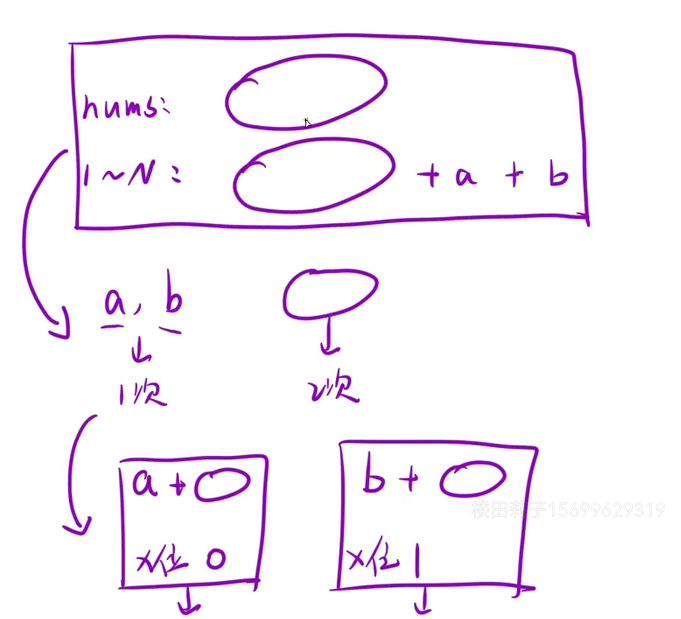
class Solution {
public:vector<int> missingTwo(vector<int>& nums) {//将所有的数字异或在一起int tmp=0;for(auto& x:nums){tmp^=x;}for(int i=0;i<=nums.size()+2;i++){tmp^=i;}//找出a和b比特位上不同的那个int diff=0;while(1){if(((tmp>>diff)&1)==1) break;else diff++;}//根据diff位不同将所有数划分为两类异或int a=0,b=0;for(int x:nums)if(((x>>diff)&1)==1) b^=x;else a^=x;for(int i=0;i<=nums.size()+2;i++)if(((i>>diff)&1)==1) b^=i;else a^=i;return {a,b};}
};本期内容就到这里了,喜欢请点个赞谢谢。
