当前位置： 首页 > news >正文

RSA的CTF题目环境和做题复现第1集

news 2025/9/2 9:47:48

1. 概念及原理

1.1 RSA算法涉及三个参数：n、e、d。

私钥由n和d组成。

公钥由n和e组成。

n和e是公开的（公钥），但n通常是两个大素数的乘积。

求解d非常困难，因为大素数分解在计算上不可行。

RSA加密的安全性基于大素数分解的难度，是一种安全的非对称加密方法。

1.2 RSA密钥生成步骤：

  1. 随机选择两个不相等的质数：选择 ( p ) 和 ( q )。
  2. 计算模数 ( n )：计算 ( n = p \times q )。( n ) 的二进制长度即为密钥长度（常见长度为1024位或2048位）。
  3. 计算欧拉函数 ( \varphi(n) )：( \varphi(n) = (p-1)(q-1) )。
  4. 选择公钥指数 ( e )：选择一个整数 ( e )，满足 ( 1 < e < \varphi(n) ) 且 ( e ) 与 ( \varphi(n) ) 互质（常用值为65537）。
  5. 计算私钥指数 ( d )：计算 ( e ) 对于 ( \varphi(n) ) 的模反元素 ( d )，即满足 ( e \times d \equiv 1 \pmod{\varphi(n)} )。
  6. 封装密钥：将 ( (n, e) ) 封装为公钥，将 ( (n, d) ) 封装为私钥。

1.3 RSA密钥生成具体示例

  1. 选择质数：随机选择两个不相等的质数 ( p = 47 ) 和 ( q = 59 )。
  2. 计算模数 ( n )：
    • ( n = p \times q = 47 \times 59 = 2773 )
    • 2773 的二进制为 101011010101，长度为 12 位，因此密钥长度为 12 位。
  3. 计算欧拉函数 ( \varphi(n) )：
    • ( \varphi(n) = (p-1)(q-1) = (47-1)(59-1) = 46 \times 58 = 2668 )
  4. 选择公钥指数 ( e )：
    • 选择 ( e = 63 )，满足 ( 1 < e < \varphi(n) ) (即 1 < 63 < 2668) 且 ( e ) 与 ( \varphi(n) ) 互质。
  5. 计算私钥指数 ( d )：
    • 计算 ( e ) 对于 ( \varphi(n) ) 的模反元素 ( d )，满足 ( e \times d \equiv 1 \pmod{\varphi(n)} )。
    • 公式为 ( 63d \equiv 1 \pmod{2668} )。
    • 通过计算（例如使用扩展欧几里得算法）得到 ( d = 847 )。
  6. 生成密钥：
    • 公钥为 ( (n, e) = (2773, 63) )。
    • 私钥为 ( (n, d) = (2773, 847) )。

1.4 加密步骤

  1. 前提条件：

    • 发送方要发送的信息是明文 ( m )。
    • 发送方从接收方获得的公钥为 ( (n, e) )。
    • 明文 ( m ) 必须是整数，并且必须满足 ( m < n )。

  2. 加密公式：
    [
    c \equiv m^e \pmod{n}
    ]

    • ( m ) 是明文，( e ) 和 ( n ) 是公钥中的参数。
    • 计算出的 ( c ) 即为加密后的信息，称为密文。

  3. 发送：发送方将密文 ( c ) 发送给接收方。

加密举例：

  • 公钥: ( (n, e) = (2773, 63) )
  • 明文: ( m = 244 ) (满足 ( m < n ))
  • 计算密文:
    [
    c \equiv 244^{63} \pmod{2773} = 465
    ]
  • 因此，得到的密文为 ( c = 465 )。

1.5

1. 公钥文件内容：

  • 通常包含两个部分：
    • 公钥模数 (N)
    • 公钥指数 (E)

2. 私钥文件内容：
私钥文件包含的信息比公钥更丰富，通常包括：

  • <1> 公钥文件的所有内容（即模数 N 和指数 E）。
  • <2> 组成公钥模数 N 的两个大素数 (p 和 q)。
  • <3> 私钥指数 (d) 以及两个用于加速计算（使用中国剩余定理CRT）的相关参数：
    • dp = d mod (p-1)
    • dq = d mod (q-1)
  • <4> CRT系数 (qInv)，即 q⁻¹ mod p。

3. 安全性：

  • 一旦攻击者获取到私钥，就意味着全部信息的泄露。
  • 攻击者可以：
    • 自由解密传输的所有密文内容。
    • 修改传输的内容。

1.6 大素数分解https://factordb.com/

在这里插入图片描述

E:\MISC\RSA\yafu-1.34

1.7 OpenSSL工具

1. OpenSSL 简介：

  • 一个功能强大的密码学工具包，集成了众多密码算法及实用工具。
  • 可用于生成密钥、证书，以及加密解密文件。
  • 通常集成在 Kali Linux 系统中。

2. 生成RSA私钥：

  • 命令：openssl genrsa -out test.key 1024
  • 功能：生成一个1024位长度的RSA私钥，并保存到 test.key 文件中。

3. 从私钥中提取公钥：

  • 命令：openssl rsa -in test.key -pubout -out test_pub.key
  • 功能：从私钥文件 test.key 中提取出公钥部分，并保存到 test_pub.key 文件中。

4. 解密文件：

  • 命令：openssl rsautl -decrypt -in hello.en -inkey test.key -out hello.de
  • 功能：使用私钥 test.key 对加密文件 hello.en 进行解密，并将解密后的内容输出到 hello.de 文件中。

1.8 rsatool工具*

1. 工具名称与用途：

  • 名称：rsatool
  • 用途：主要用于生成RSA私钥。

2. 项目地址：

  • GitHub: https://github.com/ius/rsatool

3. 基本命令格式：

  • python rsatool.py -e <公钥指数e> -p <质数p> -q <质数q> -o <输出文件名> -f <输出格式>
  • 这是一个用于从给定的参数生成私钥的命令模板。

根据您提供的文件内容，提取的关键信息如下：

工具名称： RsaCtfTool

项目地址： https://github.com/Ganapati/RsaCtfTool

(注：原内容中的 “_ Ig Bithtt” 似乎是 “GitHub” 的笔误或乱码，已根据常识和上下文修正为标准的 GitHub 地址格式。)

1.9 RSA单公钥问题

n分解为多个素数因子
适用情况: N分解后有多个因子

解决思路:
欧拉函数的性质:
对于质数 ( p, \varphi§ = (p-1) )
(\varphi(n) = (p-1)*(q-1)(r-1)^(s-1) )

1.10 n分解为多个素数因子

适用情况：N分解后有多个相同的因子

解决思路：
欧拉函数的性质：
若 ( N = p^{}k )，( \varphi(n) = p^{}k - p^{**}(k-1) )

注： 内容中的 p^{**}k 可能表示 p^k（p的k次方），这是一种不太规范的数学表达式写法。标准写法应为：

  • 若 ( N = p^k )，则 ( \varphi(N) = p^k - p^{k-1} )

1.11 维纳攻击

适用情况:e很大

解决思路:
github上有开源的攻击代码
https://github.com/pablocelayes/rsa-wiener-attack

当 ( d < (1/3)N^\wedge(1/4) ) 时，我们可以通过Wiener’sattack分解得到d

注： 内容中的 N^\wedge(1/4) 应为 N^(1/4)（N的1/4次方），这是一种不太规范的数学表达式写法。标准写法应为：

  • 当 ( d < \frac{1}{3}N^{1/4} ) 时，我们可以通过Wiener’s attack分解得到d
    在这里插入图片描述

2 题目

2.1 单公钥攻击-n分解为多个素数因子-多因子

('n=', '0xf1b234e8a03408df4868015d654dcb931f038ef4fc0be8658c9b951ee6c60d23689a1bfb151e74df0910fa1cf8a542282a65')
('e=', '0x10001')
('c=', '0x22fda6137013bac19754f78e8d9658498017f05a4b0814f2af97dc2c60fdc433d2949ea27b13337961ef3c4cf27452ad3c95')

2.2 分解N得到相同的几个p

pubkey = (58134567416061346246424950552806959952164141873988197038339318172373514096258823300468791726051378264715940131129676561677588167620420173326653609778206847514019727947838555201787320799426605222230914672691109516799571428125187628867529996213312357571123877040878478311539048041218856094075106182505973331343540958942283689866478426396304208219428741602335233702611371265705949787097256178588070830596507292566654989658768800621743910199053418976671932555647943277486556407963532026611905155927444039372549162858720397597240249353233285982136361681173207583516599418613398071006829129512801831381836656333723750840780538831405624097443916290334296178873601780814920445215584052641885068719189673672829046322594471259980936592601952663772403134088200800288081609498310963150240614179242069838645027877593821748402909503021034768609296854733774416318828225610461884703369969948788082261611019699410587591866516317251057371710851269512597271573573054094547368524415495010346641070440768673619729280827372954003276250541274122907588219152496998450489865181536173702554116251973661212376735405818115479880334020160352217975358655472929210184877839964775337545502851880977049299029101466287659419446724781305689536816523774995178046989696610897508786776845460908137698543091418571263630383061605011820139755322231913029643701770497299157169690586232187419462594477116374977216427311975598620616618808494138669546120288334682865354702356192972496556372279363023366842805886601834278434406709218165445335977049796015123909789363819484954615665668979L, 754600786340927688096652328072061561501667781193760284816393637647032362908189628005150802929636396969230958922073774180726205402897453096041624408154494621307262657492560975357997726055874834308239749992507552325614973631556754707427580134609221878324704469965450463088892083264951442562525825243127575048386573246756312509362222667015490013299327398464802116909245529065994770788125182846841016932803939806558559335886481214931253578226314057242462834149031625361286317307273138514126289052003214703248070256059405676891634792175775697355408418965738663732479622148276007308404691800186837579126431484536836513358124181380166971922188839934522356902295160649189850427580493328509329115798694580347461641487270793993129066433242544366683131231903590153844590595882428219010673818765995719694470668924781499987923250883546686344997580959954960334567874040563037167422839228466141912000421309282727363913908613116739074234989825489075148091144771967111113068647060175231126374070143480727000247378471525286907200601035581143391602569836131345909055708005758380081303860198696570649330092070410465978479841469533490522594827330661914537170063053059393550673731195548189192109328158876774080143171304333338291909598353550442855717204721L)
enc =
YXmuOsaD1W4poLAG2wPrJ/nYZCkeOh2igCYKnZA6ecCeJadT6B3ZVTciPN6LJ8AcAsRXNnkC6+9P
NJPhmosSG5UGGbpIcg2JaZ1iA8Sm3fGiFacGvQsJOqqIWb01rjaQ3rDBKB331rrNo9QNOfMnjKr0
ejGG+dNObTtvnskICbYbNnSxMxLQF57H5JnWZ3LbbKQ493vmZzwvC6iH8blNPAp3dBlVzDqIAmxm
Ubk0OzFjPoHphD1oxHdzXyQNW+sLxVldrf9xcItq92jN5sqBYrG8wADIqY1/sqhTMZvkIYFMHqoM
QuiRSnVrCF2h2RtGDEayLo0evgXI/0W3YveyKCHViOnG6wypcBFm91ZWdjp3fVW/4DyxW6xu9hg/
NlXyRP6pT/OyQpcyTqKRuiXJLWgFUJI/8TRgyAjBLLgSd3U0N3VM8kewXw5j+fMUTCW9/Gy4iP8m
52Zabx/vEKdwdGZ0QyvgvAWGUFZ96EK0g1BM/LU9Tuu2R+VKcCSCprg283x6NfYxmU26KlQE6Zrr
jLmbCOe0327uaW9aDbLxZytPYIE5ZkzhSsD9JpQBKL30dCy3UKDbcuNgB6SrDddrbIuUd0/kLxuw
h6kTqNbC4NDrOT4WAuP4se8GGOK8Wz0dL6rE6FkzMnI4Qg501MTSNQZ4Bp7cNf6H9lTa/4DNOl0=

import gmpy2
import random
from Crypto.Util.number import *
from flag import flagdef generate_key(nbit):p = getPrime(nbit)r = random.randint(2, 10)s = random.randint(r, nbit)while True:e = random.randint(3, p**r*(p-1))if gmpy2.gcd(e, p**s*(p-1)) == 1:breakpubkey = (long(e), long(p**r))return pubkeydef crypt(msg, pkey):e, n = pkeym = bytes_to_long(msg)assert m < n - 1enc = pow(m, e, n)return long_to_bytes(enc)nbit = 1024
pubkey = generate_key(nbit)
print 'pubkey =', pubkey
msg = flag
enc = crypt(msg, pubkey)
print 'enc =\n', enc.encode('base64')

2.3 维纳攻击

#coding:utf-8
from Crypto.PublicKey import RSA
from Crypto.Cipher import PKCS1_v1_5 as Cipher_pkcs1_v1_5
import base64flag=raw_input('flag:')
key=RSA.construct((
1063045321283844468344531168992778520651192162100948533991539097447031440099068191835838938460807260866872379834796862916118785271062289281267667669640800501698142693389209275376843382863579650189770597683750285863264900550873946315282419836314624717099137587285914594767991156599774939796135459567361628680491,
837165022918375318972691589169491375229372195625949131217496854325301326605410101747276306602929469715073424551708333928950600485641255979157575820275722843425977788363689955816657268540801735314259292947814991120279176324975549584376803575754002226929798448733721658019892180452857751462631173991911853793471))
cipher = Cipher_pkcs1_v1_5.new(key)
cipher_text = base64.b64encode(cipher.encrypt(flag))
print cipher_text
#cipher_text = 'Agztlhdudnheacr75FcLhYYsYa65KZ8V29bbgbf+B0yjnyx5stCYjcyhtat73ahs2E0aMgwGluJ3HwPTvT+TSLHZxM4uTnAqWQu14dnb7vF7QtzM9ShY201h26Cglnf510vQWbY7NCCTkA/orWM7F5yxZ1KRAawacS2M5ghP4/Q'

3 环境搭建

3.1

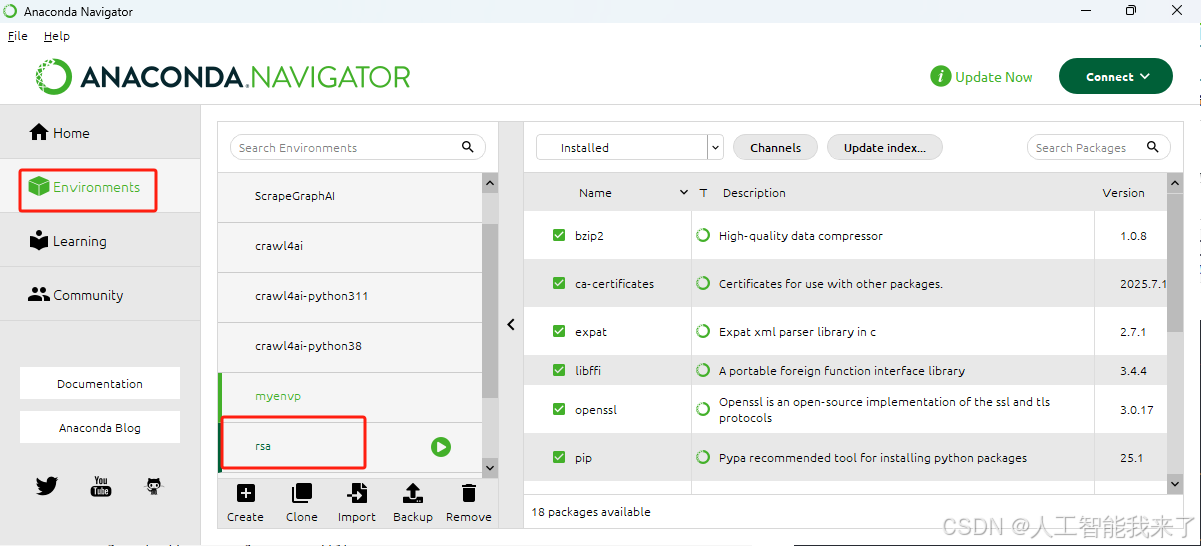
在这里插入图片描述

(rsa) C:\Users\Administrator>pip install libnum   gmpy2 pyCryptodome -i https://mirror.sjtu.edu.cn/pypi/web/simple
Looking in indexes: https://mirror.sjtu.edu.cn/pypi/web/simple
Collecting libnumDownloading https://mirror.sjtu.edu.cn/pypi-packages/5f/c7/17e4c6bf91e06c6ac1fbe2100f4761248cac960e63a4cc4d63a9c53afac0/libnum-1.7.1-py3-none-any.whl (14 kB)
Collecting gmpy2Downloading https://mirror.sjtu.edu.cn/pypi-packages/11/1b/faf855ba8bac61514c853b8e609052e550b88771ef24f4c5360d3726c82c/gmpy2-2.2.1-cp39-cp39-win_amd64.whl (1.2 MB)━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 1.2/1.2 MB 6.7 MB/s eta 0:00:00
Collecting pyCryptodomeDownloading https://mirror.sjtu.edu.cn/pypi-packages/54/2f/e97a1b8294db0daaa87012c24a7bb714147c7ade7656973fd6c736b484ff/pycryptodome-3.23.0-cp37-abi3-win_amd64.whl (1.8 MB)━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 1.8/1.8 MB 8.2 MB/s eta 0:00:00
Installing collected packages: pyCryptodome, libnum, gmpy2
Successfully installed gmpy2-2.2.1 libnum-1.7.1 pyCryptodome-3.23.0

3.2 kali

┌──(root㉿kali2023)-[~/setuptools-18.5/pip-7.1.2]
└─# wget https://bootstrap.pypa.io/pip/2.7/get-pip.py 
--2025-08-24 16:35:35--  https://bootstrap.pypa.io/pip/2.7/get-pip.py
Resolving bootstrap.pypa.io (bootstrap.pypa.io)... 198.18.0.198
Connecting to bootstrap.pypa.io (bootstrap.pypa.io)|198.18.0.198|:443... connected.
HTTP request sent, awaiting response... 200 OK
Length: 1908226 (1.8M) [text/x-python]
Saving to: 'get-pip.py'get-pip.py          100%[================>]   1.82M  3.19MB/s    in 0.6s    2025-08-24 16:35:37 (3.19 MB/s) - 'get-pip.py' saved [1908226/1908226]┌──(root㉿kali2023)-[~/setuptools-18.5/pip-7.1.2]
└─# sudo python2 get-pip.py
DEPRECATION: Python 2.7 reached the end of its life on January 1st, 2020. Please upgrade your Python as Python 2.7 is no longer maintained. pip 21.0 will drop support for Python 2.7 in January 2021. More details about Python 2 support in pip can be found at https://pip.pypa.io/en/latest/development/release-process/#python-2-support pip 21.0 will remove support for this functionality.                                                                            
Collecting pip<21.0Downloading pip-20.3.4-py2.py3-none-any.whl (1.5 MB)|################################| 1.5 MB 1.5 MB/s 
Collecting wheelDownloading wheel-0.37.1-py2.py3-none-any.whl (35 kB)
Installing collected packages: pip, wheelAttempting uninstall: pipFound existing installation: pip 7.1.2Uninstalling pip-7.1.2:Successfully uninstalled pip-7.1.2
Successfully installed pip-20.3.4 wheel-0.37.1┌──(root㉿kali2023)-[~/setuptools-18.5/pip-7.1.2]
└─# pip2 -V
pip 20.3.4 from /usr/local/lib/python2.7/dist-packages/pip (python 2.7)┌──(root㉿kali2023)-[~/setuptools-18.5/pip-7.1.2]
└─# pip2 install libnum   gmpy2 pyCryptodome -i https://mirror.sjtu.edu.cn/pypi/web/simple
DEPRECATION: Python 2.7 reached the end of its life on January 1st, 2020. Please upgrade your Python as Python 2.7 is no longer maintained. pip 21.0 will drop support for Python 2.7 in January 2021. More details about Python 2 support in pip can be found at https://pip.pypa.io/en/latest/development/release-process/#python-2-support pip 21.0 will remove support for this functionality.                                                                            
Looking in indexes: https://mirror.sjtu.edu.cn/pypi/web/simple
Collecting libnumDownloading https://mirror.sjtu.edu.cn/pypi-packages/b4/6c/c3cccd9a8e065d242cc39115728d379c8b06a98e547855be71fe59920ac7/libnum-1.6.1-py2.py3-none-any.whl (15 kB)
Collecting gmpy2Downloading https://mirror.sjtu.edu.cn/pypi-packages/51/8f/f4e0b655af2213d64eea1cc48f2fcf36bb5a358c41cbb49b1927c052a60f/gmpy2-2.1.5-cp27-cp27mu-manylinux2010_x86_64.whl (1.5 MB)|################################| 1.5 MB 1.1 MB/s 
Collecting pyCryptodomeDownloading https://mirror.sjtu.edu.cn/pypi-packages/63/1f/7ab3b6bed8450593939893fdfd535a8d5abedf0354cbe62314e8dec109d5/pycryptodome-3.23.0-cp27-cp27mu-manylinux2010_x86_64.whl (2.5 MB)|################################| 2.5 MB 660 kB/s 
Installing collected packages: libnum, gmpy2, pyCryptodome
Successfully installed gmpy2-2.1.5 libnum-1.6.1 pyCryptodome-3.23.0┌──(root㉿kali2023)-[~/setuptools-18.5/pip-7.1.2]
└─#

4 解题过程

4.1 exp

(rsa) C:\Users\Administrator>python
Python 3.10.6 (tags/v3.10.6:9c7b4bd, Aug  1 2022, 21:53:49) [MSC v.1932 64 bit (AMD64)] on win32
Type "help", "copyright", "credits" or "license" for more information.
>>> 0xf1b234e8a03408df4868015d654dcb931f038ef4fc0be8658c9b951ee6c60d23689a1bfb151e74df0910fa1cf8a542282a65
2437967874789105904411947653432691349095923918884760052950045400158911103839254371432240594689408409040149264634500098661
>>>

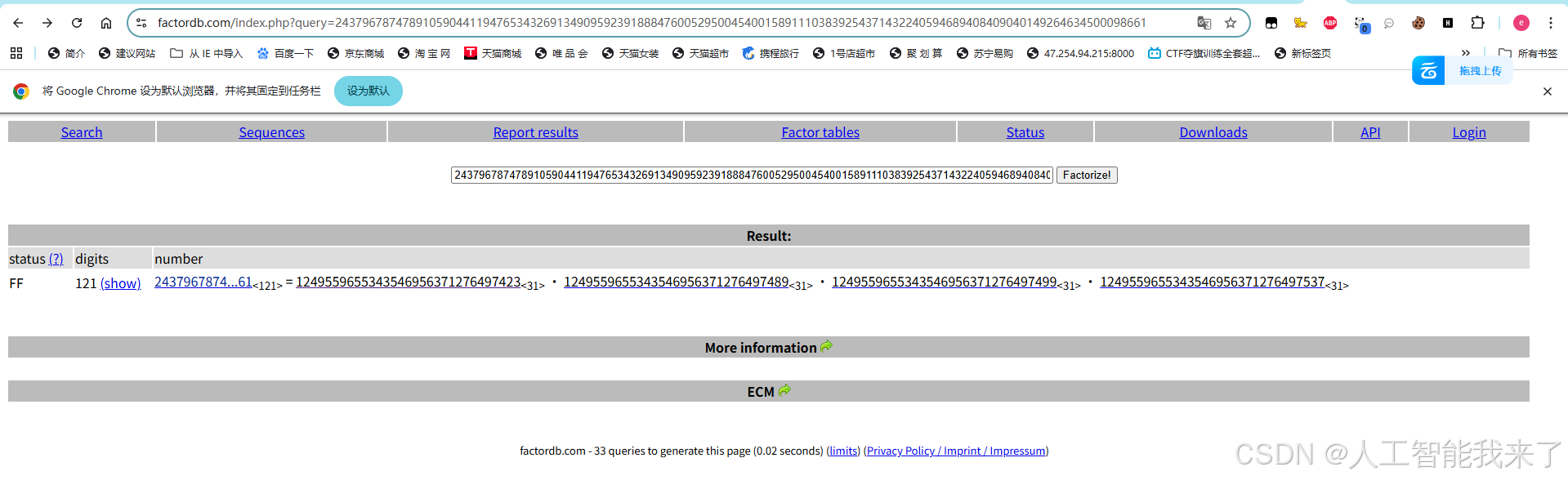
在这里插入图片描述

E:\MISC\RSA\yafu-1.34>yafu-x64.exe factor(2437967874789105904411947653432691349095923918884760052950045400158911103839254371432240594689408409040149264634500098661)fac: factoring 2437967874789105904411947653432691349095923918884760052950045400158911103839254371432240594689408409040149264634500098661
fac: using pretesting plan: normal
fac: no tune info: using qs/gnfs crossover of 95 digits
div: primes less than 10000
fmt: 1000000 iterations
fac: factoring 1561399332262283857677209135468389766374656894119412188280011
fac: using pretesting plan: normal
fac: no tune info: using qs/gnfs crossover of 95 digits
div: primes less than 10000
fmt: 1000000 iterations
Total factoring time = 0.0085 seconds
fac: factoring 1561399332262283857677209135433402096025037579341016446347151
fac: using pretesting plan: normal
fac: no tune info: using qs/gnfs crossover of 95 digits
div: primes less than 10000
fmt: 1000000 iterations
Total factoring time = 0.0080 seconds
Total factoring time = 0.0441 seconds***factors found***P31 = 1249559655343546956371276497499
P31 = 1249559655343546956371276497489
P31 = 1249559655343546956371276497537
P31 = 1249559655343546956371276497423ans = 1E:\MISC\RSA\yafu-1.34>

# -*- coding: utf-8 -*-
import binascii
import gmpy2
p=1249559655343546956371276497423
q=1249559655343546956371276497489
r=1249559655343546956371276497499
s=1249559655343546956371276497537
e=0x10001
c=0x22fda6137013bac19754f78e8d9658498017f05a4b0814f2af97dc2c60fdc433d2949ea27b13337961ef3c4cf27452ad3c95
n=p*q*r*sphi=(p-1)*(q-1)*(r-1)*(s-1)
d=gmpy2.invert(e,phi)
m=pow(c,d,n)
print(binascii.unhexlify(hex(m)[2:].strip("L")))

在这里插入图片描述
flag is:testflag

4.2 exp

#!/usr/bin/python
#coding:utf-8
#Author:醉清风import base64
import gmpy2
import libnum
from Crypto.Util.number import long_to_bytes,bytes_to_longc = "YXmuOsaD1W4poLAG2wPrJ/nYZCkeOh2igCYKnZA6ecCeJadT6B3ZVTciPN6LJ8AcAsRXNnkC6+9PNJPhmosSG5UGGbpIcg2JaZ1iA8Sm3fGiFacGvQsJOqqIWb01rjaQ3rDBKB331rrNo9QNOfMnjKr0ejGG+dNObTtvnskICbYbNnSxMxLQF57H5JnWZ3LbbKQ493vmZzwvC6iH8blNPAp3dBlVzDqIAmxmUbk0OzFjPoHphD1oxHdzXyQNW+sLxVldrf9xcItq92jN5sqBYrG8wADIqY1/sqhTMZvkIYFMHqoMQuiRSnVrCF2h2RtGDEayLo0evgXI/0W3YveyKCHViOnG6wypcBFm91ZWdjp3fVW/4DyxW6xu9hg/NlXyRP6pT/OyQpcyTqKRuiXJLWgFUJI/8TRgyAjBLLgSd3U0N3VM8kewXw5j+fMUTCW9/Gy4iP8m52Zabx/vEKdwdGZ0QyvgvAWGUFZ96EK0g1BM/LU9Tuu2R+VKcCSCprg283x6NfYxmU26KlQE6ZrrjLmbCOe0327uaW9aDbLxZytPYIE5ZkzhSsD9JpQBKL30dCy3UKDbcuNgB6SrDddrbIuUd0/kLxuwh6kTqNbC4NDrOT4WAuP4se8GGOK8Wz0dL6rE6FkzMnI4Qg501MTSNQZ4Bp7cNf6H9lTa/4DNOl0="e = 58134567416061346246424950552806959952164141873988197038339318172373514096258823300468791726051378264715940131129676561677588167620420173326653609778206847514019727947838555201787320799426605222230914672691109516799571428125187628867529996213312357571123877040878478311539048041218856094075106182505973331343540958942283689866478426396304208219428741602335233702611371265705949787097256178588070830596507292566654989658768800621743910199053418976671932555647943277486556407963532026611905155927444039372549162858720397597240249353233285982136361681173207583516599418613398071006829129512801831381836656333723750840780538831405624097443916290334296178873601780814920445215584052641885068719189673672829046322594471259980936592601952663772403134088200800288081609498310963150240614179242069838645027877593821748402909503021034768609296854733774416318828225610461884703369969948788082261611019699410587591866516317251057371710851269512597271573573054094547368524415495010346641070440768673619729280827372954003276250541274122907588219152496998450489865181536173702554116251973661212376735405818115479880334020160352217975358655472929210184877839964775337545502851880977049299029101466287659419446724781305689536816523774995178046989696610897508786776845460908137698543091418571263630383061605011820139755322231913029643701770497299157169690586232187419462594477116374977216427311975598620616618808494138669546120288334682865354702356192972496556372279363023366842805886601834278434406709218165445335977049796015123909789363819484954615665668979p = 165740755190793304655854506052794072378181046252118367693457385632818329041540419488625472007710062128632942664366383551452498541560538744582922713808611320176770401587674618121885719953831122487280978418110380597358747915420928053860076414097300832349400288770613227105348835005596365488460445438176193451867n = p**4phi = p**4-p**3
#c = int(base64.b64decode(c).encode('hex'),16) 延伸
c = bytes_to_long(c.decode('base64'))
d = gmpy2.invert(e,phi)
m = pow(c,d,n)
print long_to_bytes(m)

在这里插入图片描述
flag{ec33f669d2d659e2bc27dbffdfeb0f38}

4.3 wienerAttack exp

# coding: utf-8
import gmpy2
import base64
from Crypto.Util.number import long_to_bytes,bytes_to_long
def transform(x,y):       #使用辗转相处将分数 x/y 转为连分数的形式res=[]while y:res.append(x//y)x,y=y,x%yreturn resdef continued_fraction(sub_res):numerator,denominator=1,0for i in sub_res[::-1]:      #从sublist的后面往前循环denominator,numerator=numerator,i*numerator+denominatorreturn denominator,numerator   #得到渐进分数的分母和分子，并返回#求解每个渐进分数
def sub_fraction(x,y):res=transform(x,y)res=list(map(continued_fraction,(res[0:i] for i in range(1,len(res)))))  #将连分数的结果逐一截取以求渐进分数return resdef get_pq(a,b,c):      #由p+q和pq的值通过维达定理来求解p和qpar=gmpy2.isqrt(b*b-4*a*c)   #由上述可得，开根号一定是整数，因为有解x1,x2=(-b+par)//(2*a),(-b-par)//(2*a)return x1,x2def wienerAttack(e,n):for (d,k) in sub_fraction(e,n):  #用一个for循环来注意试探e/n的连续函数的渐进分数，直到找到一个满足条件的渐进分数if k==0:                     #可能会出现连分数的第一个为0的情况，排除continueif (e*d-1)%k!=0:             #ed=1 (mod φ(n)) 因此如果找到了d的话，(ed-1)会整除φ(n),也就是存在k使得(e*d-1)//k=φ(n)continuephi=(e*d-1)//k               #这个结果就是 φ(n)px,qy=get_pq(1,n-phi+1,n)if px*qy==n:p,q=abs(int(px)),abs(int(qy))     #可能会得到两个负数，负负得正未尝不会出现d=gmpy2.invert(e,(p-1)*(q-1))     #求ed=1 (mod  φ(n))的结果，也就是e关于 φ(n)的乘法逆元dreturn dprint("该方法不适用")e = 837165022918376318972691589160491375229372195625940137121740685432530132860541010174727630660292946071507342455170833392895060048564125597915757582027572284342507277083636059558106672685400173531425920294781499112027917632497954958437660357575400222692979844873372105801998210845285775146263117399191185379347
n = 1063045321283844468344531168992778520651192162100948533991539097447031440090068191835838938460807260866872379834796862916118785271062209281267667069640000501698142693389209275376843382863579650119977059768375028586326490055087394631528241983631462471709913758728591459476799115050977493979613545056736162868049
d=wienerAttack(e,n)
print("d=",d)
c1='AGgt1h6dudnkeoCr7SFclkYYsYa65KZ8V29bbgbf+BDyjnyx5stCYjcyktat73aHs2EOaMgwGUwj3HwPTvT+T5LHIxM4uTnAgWOui4dnb7vF7QizN0ShY2O1h26CgLnf5I0vQWbY7WCC7kA/orNW7F5yxZiKRAawacS2M5ghP4/Q'
c = bytes_to_long(base64.b64decode(c1))
flag=long_to_bytes(pow(c,d,n))
print(flag)

在这里插入图片描述
flag{nell_anima_ritrovo_la_speranza_che_nel_corpo_stanco_ormai}

http://www.xdnf.cn/news/1422595.html

相关文章：

  • shell——函数与数组
  • 华东制造企业推荐的SD-WAN服务商排名
  • java中常见的几种排序算法
  • 毕业设计：丹麦电力电价预测预测未来24小时的电价pytorch+lstm+历史特征和价格+时间序列 电价预测模型资源 完整代码数据可直接运行
  • js脚本和ts脚本相互调用
  • 虚拟机一插SD卡就蓝屏，导致整个电脑系统蓝屏怎么办
  • 一、SVN与svnbucket.com常见问题解答
  • PTP高精度时间同步的核心：E2E与P2P延迟补偿机制
  • FPGA|Quartus II 中pll IP核的具体使用方法
  • 优化正则表达式性能：预编译与模式匹配的最佳实践
  • Coolutils Total PDF Converter中文版：多功能PDF文件转换器
  • 奇偶破题：当反函数撞上奇函数
  • 【前端:Html】--4.进阶：媒体
  • 【论文阅读】Sparse4D v3：Advancing End-to-End 3D Detection and Tracking
  • 订单后台管理系统-day07菜品模块
  • MIT 6.5840 (Spring, 2024) 通关指南——Lab 2: Key/Value Server
  • openssh 安装部署
  • 【Day 41】Shell脚本-循环
  • 802.11 和 802.1X
  • 谷歌-PCR-CA-联合训练并行小码本引入语义特征
  • wpf之WrapPanel
  • RAG-文本到SQL
  • 国别域名的SEO优势：是否更利于在当地搜索引擎排名？
  • Linux -- 进程间通信【System V共享内存】
  • 软考中级习题与解答——第二章_程序语言与语言处理程序（1）
  • vue社区网格化管理系统（代码+数据库+LW）
  • PRACH物理层详解
  • Flutter Container 阴影设置指南 2025版
  • 【技术选型】大型移动端跨平台应用开发 Flutter VS React Native
  • Web网络开发 -- Vue2基础语法，属性和生命周期