特征增强方法【特征构建】
文章目录
- 前言
- 特征增强
- 一维特征
- 傅里叶变换(FT)
- 意义
- 基本思想
- 经验模态分解(EMD)
- 处理流程
- 二维特征
- 时间波形到时频图
- 短时傅里叶变换(STFT)
- 图像编码方法
- 格兰姆角场
- 短时傅里叶变换 VS 格兰姆角场
前言
本篇博客主要介绍了时序数据的特征增强方法,可以分为两大类,分别是一维和二维。时序数据本身是一维的,直接增强其特征主要方式有傅里叶变换(FT)与经验模态分解(EMD),也可以通过转到二维数据(图像),主要介绍了短时傅里叶变换与格兰姆角场两种方式,这个图像往往蕴含着原时序数据中丰富的信息,将视觉领域处理图像的方式来处理我们的二维数据,进而达到特征增强的目的。
特征增强
所谓特征增强,就是通过对原始数据进行一系列操作和变换,提取/创建出更具代表性和区分性的特征,以增强数据的表现能力和模型的预测能力。
一维特征
傅里叶变换(FT)
意义
傅里叶变换可以将时域信号转换为频域信号,首先有一个问题,这样的转换有何意义?
这是一个非常核心且重要的问题。
最根本的意义在于:它为我们提供了一个全新的视角来分析和理解信号,这个视角往往比原始的时域视角更强大、更深刻。
我们可以用一个生动的比喻来理解:
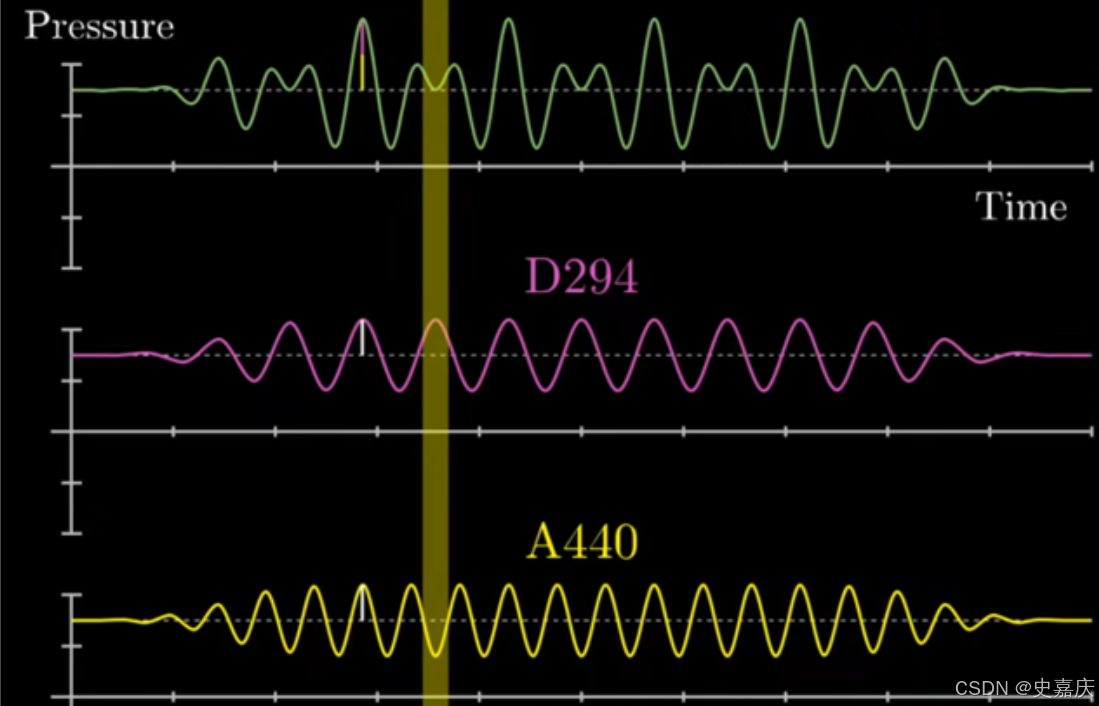
- 时域:就像是在听一首交响乐。你听到的是所有乐器声音混合在一起的结果,随着时间流逝的总体效果。你能知道音乐何时激昂、何时平缓(振幅变化),但很难精确地说出“在第30秒时,小提琴的A音有多响”。
- 频域:就像是拿到了这首交响乐的乐谱。乐谱不会告诉你某一刻整体的声音有多大,但它会精确地列出这首曲子用了哪些音符(频率成分),以及每个音符的强度(振幅)和开始时间(相位)。你可以清晰地看到长笛、双簧管、小提琴各自负责哪些音高。
基于这个比喻,傅里叶变换的意义具体体现在以下3个方面:
1. 揭示信号的“组成成分"
任何复杂的信号都可以看作是许多个不同频率、不同振幅、不同相位的简单正弦波的叠加。傅里叶变换就像一台“数学显微镜”,能够将这些混合在一起的成分分解开来,并精确地告诉我们:
- 信号中存在哪些频率成分? (有哪些“音符”?)
- 每个频率成分的强度(振幅)有多大? (这个“音符”弹奏得多响?)
- 每个频率成分的初始相位是多少? (这个“音符”何时开始?)
这在工程上是革命性的。例如:
- 音频处理:你可以通过频域分析看到一段音乐中低音、中音、高音的分布,然后通过滤波器(如均衡器)增强或削弱特定频段。
- 故障诊断:一台旋转的机器,其振动信号在时域可能只是一条杂乱无章的波形。但转换到频域后,可能会在特定的频率点出现异常高的峰值,这正好对应了某个轴承的故障特征频率,从而实现精准诊断。
2. 简化复杂的数学运算
在时域中非常困难的运算,在频域中可能会变得极其简单。最经典的例子是卷积(Convolution)。
- 时域的卷积 等于 频域的乘法。
- 卷积运算(涉及积分和滑动)计算量非常大。
- 而乘法运算则简单快速得多。
因此,许多领域的应用(如图像处理中的滤波、通信系统中的信号调制解调)都会先将信号通过傅里叶变换转到频域,进行简单的乘法操作后,再通过逆傅里叶变换转回时域。这大大提高了计算效率。
3. 实现滤波和降噪
这是第2点的直接应用。既然频域清晰地展示了信号的组成,那么去除噪声就变成了一个非常直观的操作:
- 噪声通常是特定频率的(比如50Hz的工频干扰),或者在频域上有明显的分布特征。
- 在频域中,我们可以直接衰减或清零这些噪声频率成分的强度。
- 然后再通过逆傅里叶变换转换回时域,就得到了一个去噪后的干净信号。
这种方法比很多时域滤波方法更直接、更有效。
傅里叶变换有一个巨大的假设:信号是平稳的,即其频率成分在整个时间范围内都不变。这在实际应用中往往不成立。
例如,一首音乐的频率成分是随时间剧烈变化的;一段语音信号,不同的词对应不同的频率组合。
- 傅里叶变换的缺点:它只能告诉我们“整个信号中存在哪些频率”,但无法告诉我们这些频率成分是在什么时候出现的。它丢失了所有的时间信息。
为了解决这个问题,才发展出了短时傅里叶变换(STFT)、小波变换 等时频分析方法。它们通过引入“时间窗”的概念,实现了对信号局部频率特性的分析,既能看频率,也能看时间。
| 视角 | 时域 (Time Domain) | 频域 (Frequency Domain) |
|---|---|---|
| 横坐标 | 时间 (Time) | 频率 (Frequency) |
| 纵坐标 | 振幅 (Amplitude) | 振幅 (Amplitude) / 功率 |
| 观察内容 | 信号随时间如何变化 | 信号由哪些频率组成 |
| 优点 | 直观,能看到信号随时间的完整演变过程 | 能精确分析信号的成分,简化运算,方便滤波 |
| 缺点 | 难以分析具体的频率成分 | 丢失了时间信息(针对全局FT) |
| 类比 | 听一首完整的交响乐 | 看这首交响乐的乐谱 |
因此,傅里叶变换的意义在于,它为我们提供了除时域之外的第二个维度(频域)来剖析信号,使得信号分析和处理的能力得到了质的飞跃。
基本思想
将一个时域信号分解为多个不同频率的正弦波和余弦波的叠加。
3Blue1Brown动画展示傅里叶变换原理
经验模态分解(EMD)
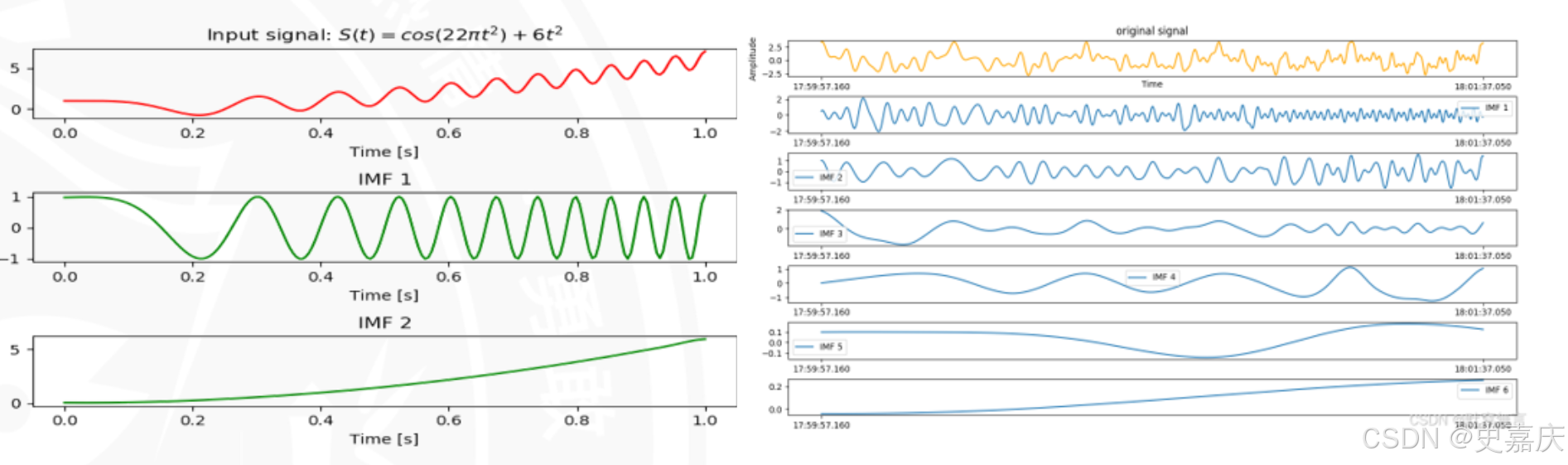
EMD是美国NASA的黄锷博士提出的一种针对非平稳信号的分析方法。EMD过程实质上是对非平稳信号进行平稳化处理的一种手段,其结果是将信号中不同尺度的波动和趋势进行逐级分解,产生一系列具有不同特征尺度的数据序列,每一个序列称为一个固有模态函数(IMF)。 IMF本质上是不同时间尺度的时序特征提取器。
• 高频 IMF → 捕捉噪声和快速波动
• 中频 IMF → 描述周期性变化
• 低频 IMF → 提取长期趋势
它们既能用于信号解释,也能作为机器学习 / 深度学习的输入特征,提高预测效果和稳定性。
处理流程
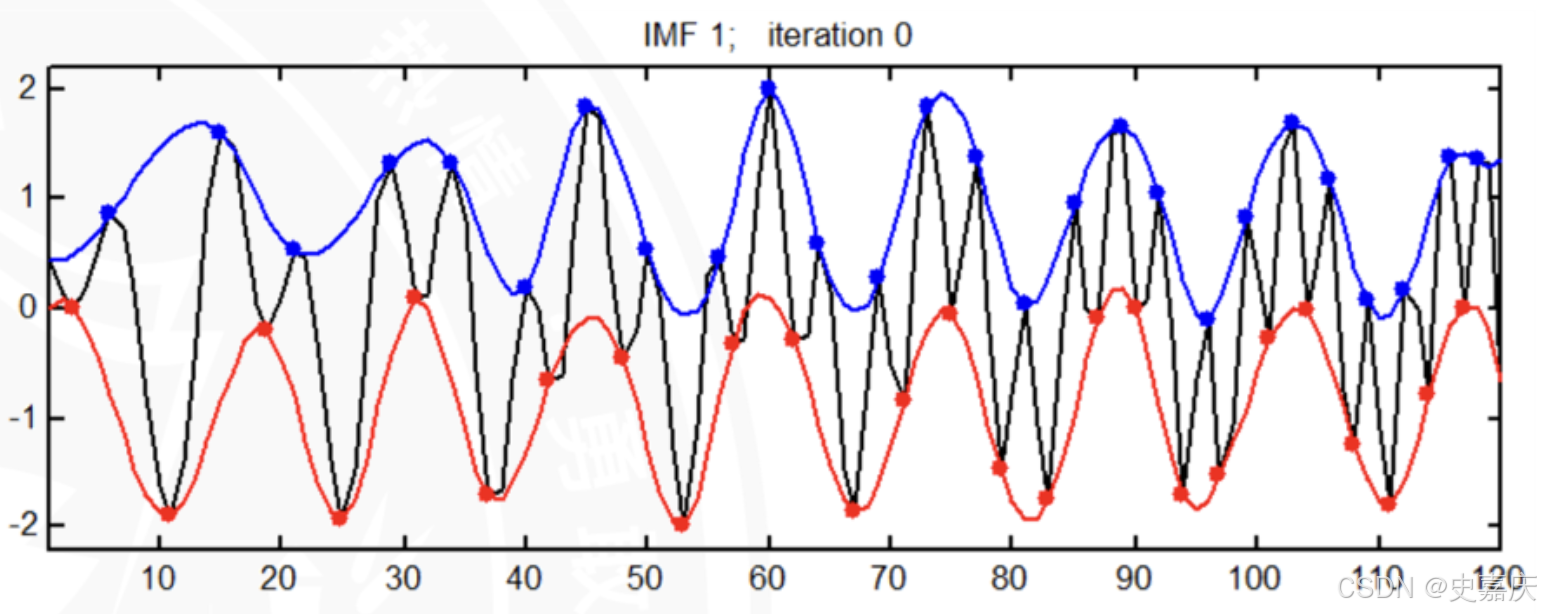
1.找到信号的全部极值点,通过三次样条插值连接极大值点构成上包络线,连接极小值点构成下包络线
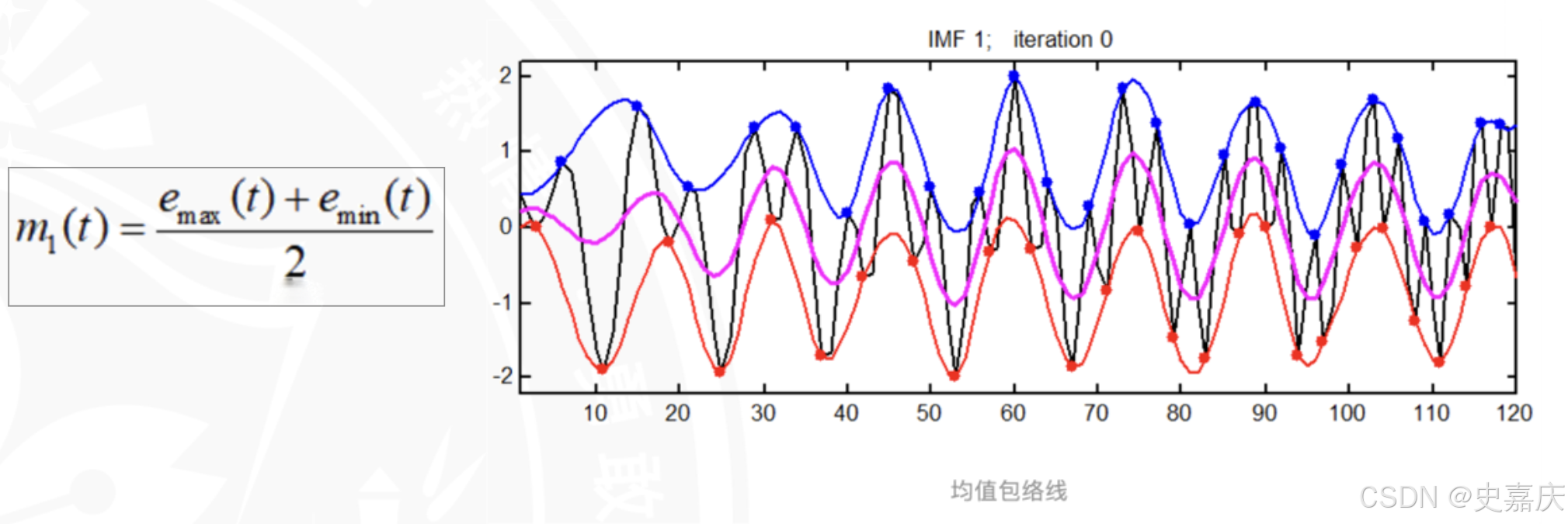
2.计算上包络和下包络线的平均值,记为m1(t)m_1(t)m1(t)
3.原始信号减去均值包络线,得到中间信号。这个过程称为筛分,即原始信号x(t)x(t)x(t)经过一次筛分得到一个新的信号(中间信号)C1,1(t)C_{1,1}(t)C1,1(t)
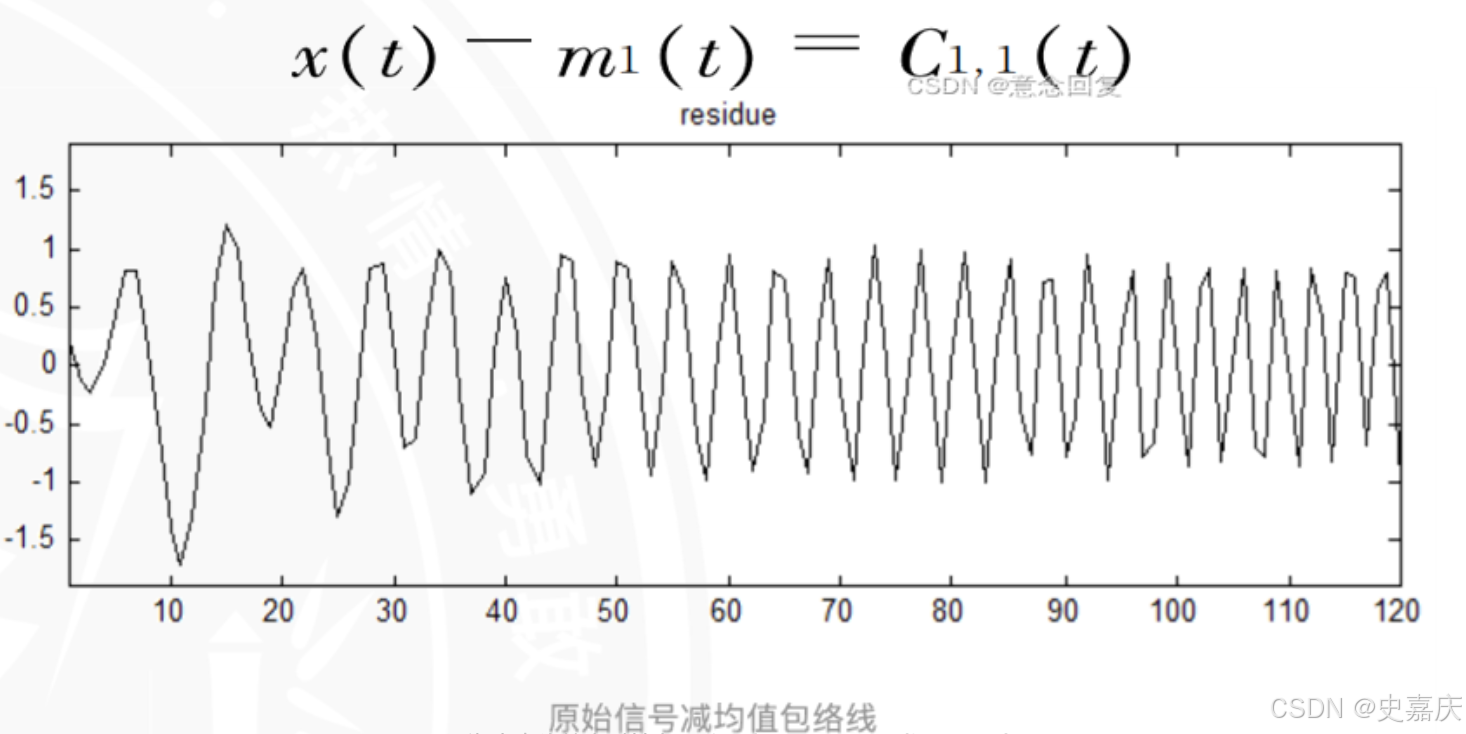
4.判断该中间信号C1,1(t)C_{1,1}(t)C1,1(t)是否满足IMF的两个条件,若满足,则该中间信号就是一个 IMF分量;如果不是,以该信号为基础,继续步骤- ~步骤四的分析,直至分解 k次后得到的信号满足IMF两个条件,作为原始信号的第一个IMF分量。
- IMF需要满足的两个条件
条件1:在整个时程内极值点个数与过零点个数相等或最多相差1。

条件二:在任意时刻,由局部极大值点形成的上包络线和由局部极小值点形成的下包络线的平均值需为0,即上、下包络线相对于时间轴局部对称
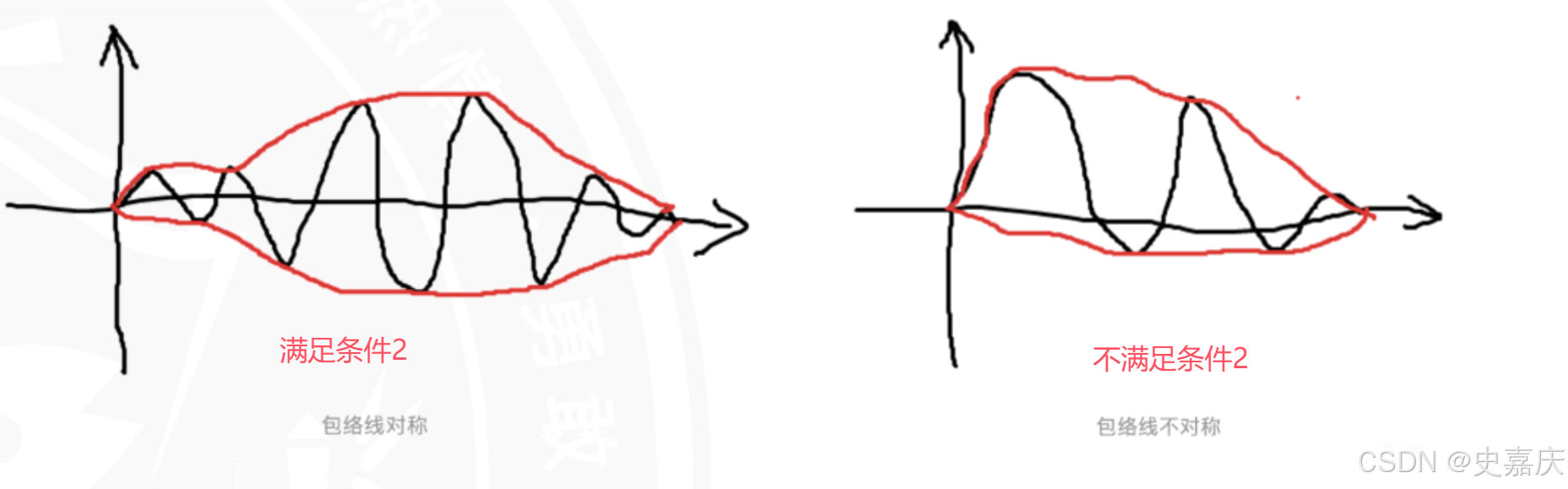
5.分解得到第一个IMF分量I1(t)I_1(t)I1(t)后,从原始信号x(t)x(t)x(t)中减去I1(t)I_1(t)I1(t)得到剩余分量r1(t)r_1(t)r1(t),接着对r1(t)r_1(t)r1(t)重复上述分解筛选处理,以此迭代,直到最后一个信号无法继续分解为止,最后一个信号即残余/残差信号(单调函数,周期大于信号的记录长度,作为趋势项)
x(t)=∑i=1nIi(t)+rn(t)x(t) = \sum_{i=1}^n I_i(t) + r_n(t)x(t)=i=1∑nIi(t)+rn(t)
二维特征
传统处理一维序列的模型(如RNN, LSTM)更侧重于时间依赖关系,但在捕捉不同时间尺度上的复杂模式组合方面,不如CNN在图像上那么高效和强大。将一维时间序列转换为二维图像,其核心意义在于:利用计算机视觉(CV)领域的强大工具和模型(尤其是卷积神经网络CNN)来解决复杂的时序问题。
在了解时序数据如何提取二维特征之前,我们有必要先知道时频图这个概念,因为我们的二维特征说白了就是一张时频图。
时间波形到时频图
时频分析:同时包含信号时间和频率信息的图形表示–时频图
首先,要理解时频图的用处,得先知道它的核心思想:它同时展示了信号在时间和频率上的能量分布。
时域图(波形图):只能告诉我们信号强度随时间的变化(什么时候声音大,什么时候声音小),但完全不知道这个信号是由哪些频率组成的。频域图(频谱图):只能告诉我们信号中包含了哪些频率成分以及它们的强度(有多少低音,多少高音),但完全不知道这些频率是在什么时间出现的。
而时频图完美地解决了这个矛盾,它告诉我们:在某个特定时间点,出现了哪些特定频率的成分,其强度如何。
下面这幅图中,上面的部分是波形图,下面是其对应的时频图。
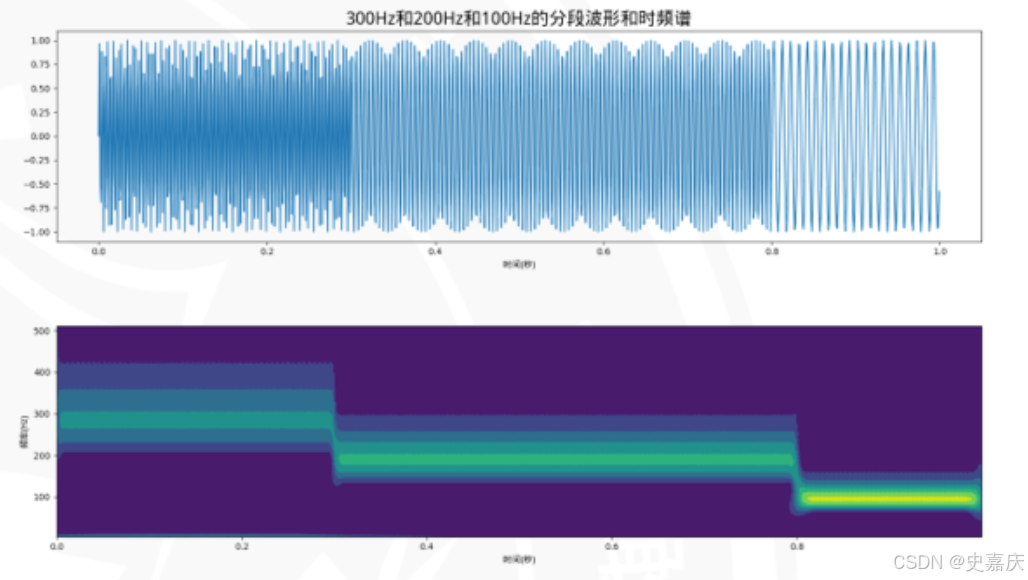
短时傅里叶变换(STFT)
STFT:一种将信号分割成短时间段,并在每个时间段内进行傅里叶变换的方法。通过STFT 这种方式,STFT能同时提供信号在时间和频率上的局部信息,适用于分析非平稳信号。
在机械系统中,轴承是最容易发生故障的关键部件之一。为了能够及时发现和诊断问题,常用的方法之一就是时频分析。短时傅里叶变换(STFT),将正常和不同故障状态下的轴承信号转化为直观的时频图,并对比了不同窗口大小下的表现。
下面结合轴承故障诊断的实际案例,详细介绍STFT的原理。
我从西储大学轴承数据集中选取了四种状态的振动信号:
正常状态
内圈故障(0.021英寸)
滚珠故障(0.021英寸)
外圈故障(0.021英寸)
import numpy as np
from scipy.io import loadmat
import numpy as np
from scipy.signal import stft
import matplotlib.pyplot as plt
import matplotlib
matplotlib.rc("font", family='Microsoft YaHei')# 读取MAT文件
data1 = loadmat('0_0.mat') # 正常信号
data2 = loadmat('21_1.mat') # 0.021英寸 内圈
data3 = loadmat('21_2.mat') # 0.021英寸 滚珠
data4 = loadmat('21_3.mat') # 0.021英寸 外圈
# 注意,读取出来的data是字典格式,可以通过函数type(data)查看。
# DE - drive end accelerometer data 驱动端加速度数据
data_list1 = data1['X097_DE_time'].reshape(-1)
data_list2 = data2['X209_DE_time'].reshape(-1)
data_list3 = data3['X222_DE_time'].reshape(-1)
data_list4 = data4['X234_DE_time'].reshape(-1)
# 划窗取值(大多数窗口大小为1024)
data_list1 = data_list1[0:1024]
data_list2 = data_list2[0:1024]
data_list3 = data_list3[0:1024]
data_list4 = data_list4[0:1024]x_list = [x for x in range(1024)]
首先,我们观察四种状态的时域波形:
plt.figure(figsize=(20,10))plt.subplot(2,2,1)
plt.plot(data_list1)
plt.title('正常')
plt.subplot(2,2,2)
plt.plot(data_list2)
plt.title('内圈')
plt.subplot(2,2,3)
plt.plot(data_list3)
plt.title('滚珠')
plt.subplot(2,2,4)
plt.plot(data_list4)
plt.title('外圈')plt.show()
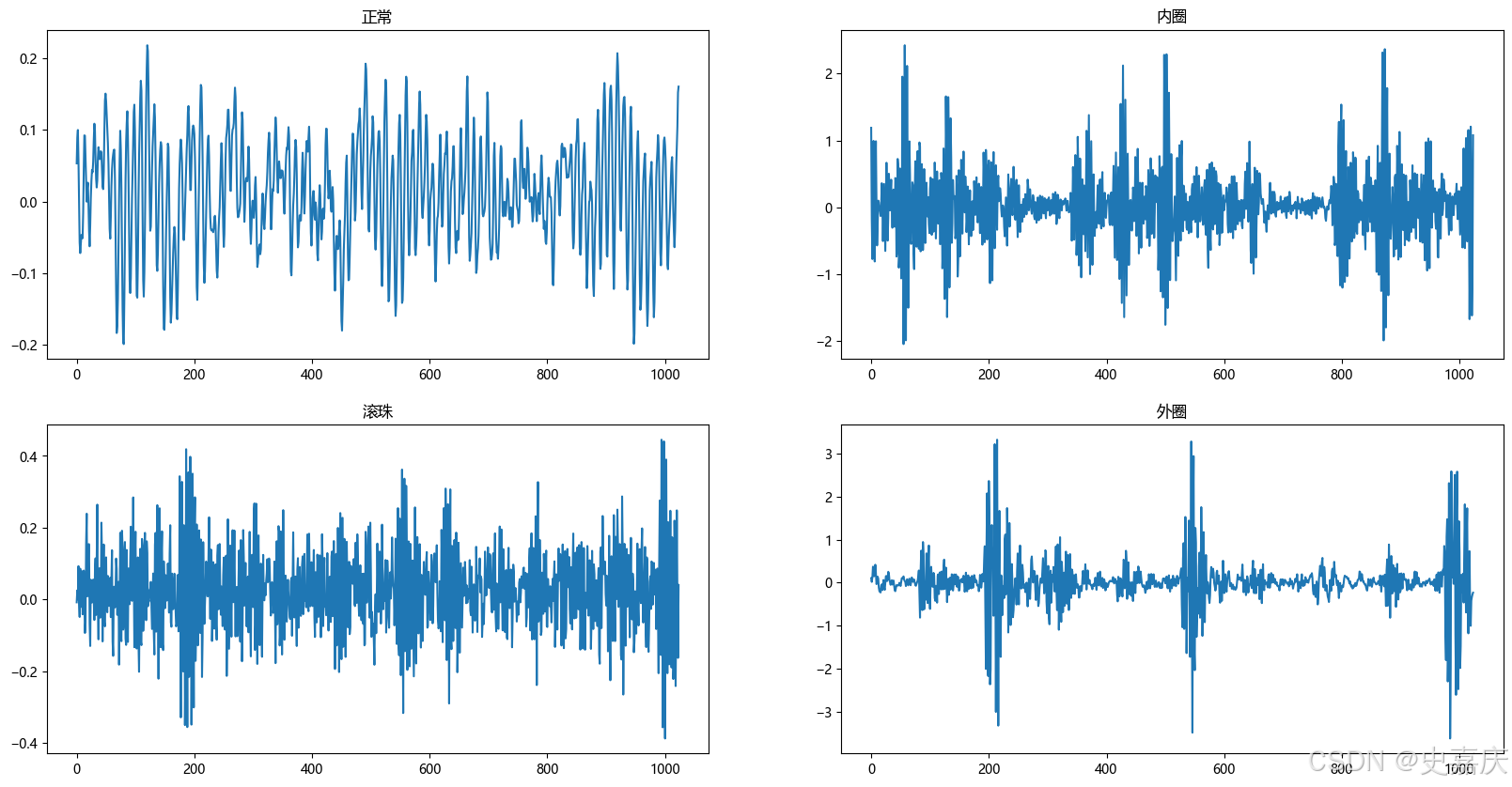
①选择窗函数:根据应用需求选择合适的窗函数并确定其长度T。
可以从以下三方面考虑窗函数的选择。
应用需求:不同应用对时频分辨率的要求不同如音频分析更注重频率分辨率,语音识别更注重时间分辨率。信号特性:信号的瞬态变化和频率变化速率决定了窗函数的长度和形状。计算复杂度:简单的窗函数(如矩形窗)计算效率高,但频谱性能较差;复杂的窗函数(如布莱克曼窗)计算复杂度高,但频谱性能优越。
| 窗口类型 | 优点 | 缺点 |
|---|---|---|
| 矩形窗 | 简单易用;计算效率高;主瓣宽度窄,频率分辨率高。 | 旁瓣高度大,频谱泄漏严重;对频域的影响较大。 |
| 汉宁窗 | 旁瓣衰减较快,频谱泄漏较少;平衡了频率分辨率和旁瓣衰减。 | 主瓣比矩形窗宽,频率分辨率略低。 |
| 海明窗 | 旁瓣衰减比汉宁窗更快,频谱泄漏更少;适合一般信号处理。 | 主瓣比汉宁窗宽,频率分辨率进一步降低。 |
| 布莱克曼窗 | 旁瓣衰减非常快,频谱泄漏最少;适用于需要极低旁瓣的应用。 | 主瓣非常宽,频率分辨率最低;计算量较大。 |
下面我们使用的是stft默认的窗函数(汉宁窗 )
import numpy as np
import matplotlib.pyplot as plt
from scipy.signal import stft# 生成三个不同频率成分的信号
fs = 1000 # 采样率
t = np.linspace(0, 1, fs, endpoint=False) # 时间# 第一个频率成分
signal1 = np.sin(2 * np.pi * 50 * t)
# 第二个频率成分
signal2 = np.sin(2 * np.pi * 120 * t)
# 第三个频率成分
signal3 = np.sin(2 * np.pi * 300 * t)# 合并三个信号
signal = np.concatenate((signal1, signal2, signal3))# 进行短时傅里叶变换
# nperseg 参数表示每个段的长度 , noverlap 表示相邻段的重叠部分,默认为汉宁窗
f, t, spectrum = stft(signal, fs, nperseg=100, noverlap=50)
# 汉宁窗优势:
# 良好的平衡性:在时间分辨率和频率分辨率之间取得较好平衡
# 较低的频谱泄漏:相比矩形窗有更好的旁瓣抑制
# 计算效率:计算相对简单
# 广泛适用性:适合大多数信号处理应用# 绘制时频图
plt.pcolormesh(t, f, np.abs(spectrum), shading='gouraud')
plt.title('STFT Magnitude')
plt.ylabel('Frequency [Hz]')
plt.xlabel('Time [sec]')
plt.show()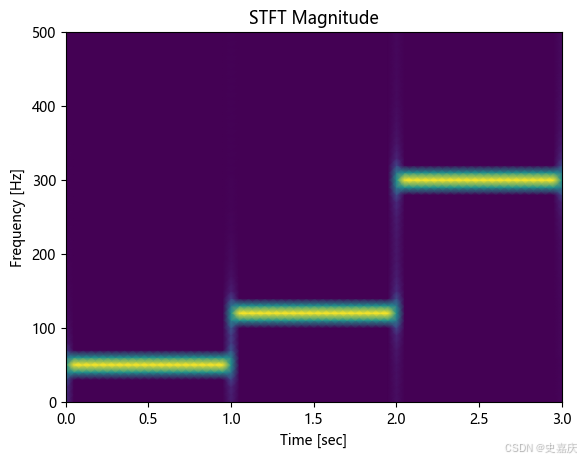
②设定帧移(Hop Size):帧移决定了窗函数在时间轴上的滑动步长,常见的帧移为窗函数长度的50%或75%。
上面代码中,这行代码已经设定了Hop Size=50%
# nperseg 参数表示每个段的长度 , noverlap 表示相邻段的重叠部分
f, t, spectrum = stft(signal, fs, nperseg=100, noverlap=50)
③分割信号:将信号分割为多个重叠的短时间帧每帧长度为窗函数长度T。
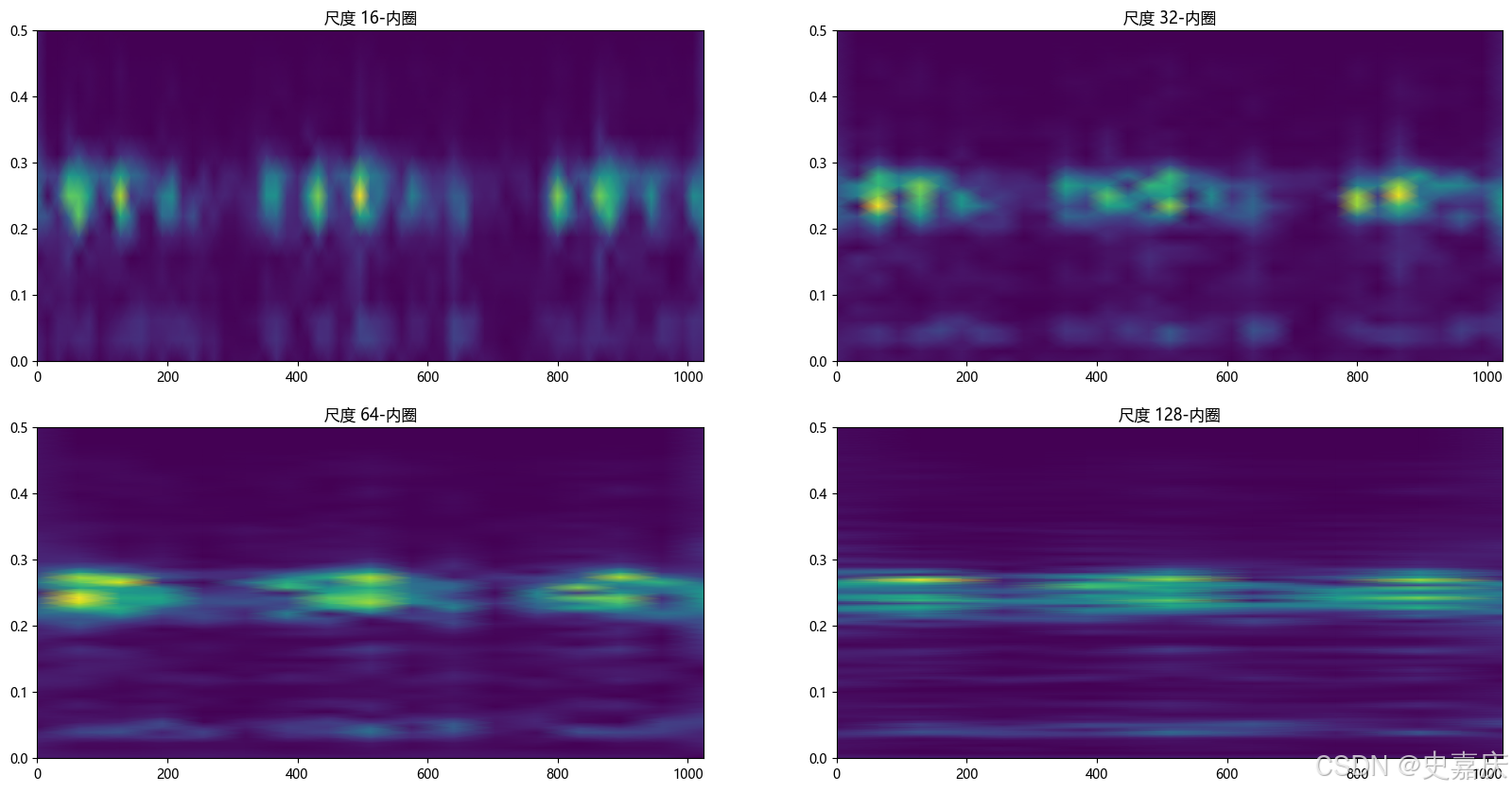
我们使用不同窗口大小(16, 32, 64, 128)对信号进行STFT分析:
④窗函数应用:对每个帧乘以窗函数,得到加窗后的信号片段。
⑤FFT计算:对每个窗函数应用后的帧进行FFT得到频域表示。
# 可视化做准备
plt.pcolormesh(t, f, np.abs(spectrum), shading='gouraud')
plt.axis('off') # 设置图像坐标轴不可见
# plt.gca().xaxis.set_major_locator(plt.NullLocator())
# plt.gca().yaxis.set_major_locator(plt.NullLocator()) # 设置坐标轴的刻度线为空,即不显示刻度。
plt.subplots_adjust(top=1, bottom=0, right=1, left=0, hspace=0, wspace=0) # 调整子图的位置和间距,将子图充满整个图像
plt.margins(0, 0) #设置图像的边距为0,即没有额外的空白边框。
plt.gcf().set_size_inches(224/100, 224/100) # 设置图像的大小,单位为英寸
plt.savefig('test', dpi=100)
plt.clf() #避免内存溢出
plt.close() #释放内存
from scipy.signal import stft# 设置STFT参数
window_size = 16 # 窗口大小
overlap = 0.5 # 重叠比例
# 计算重叠的样本数
overlap_samples = int(window_size * overlap)
frequencies1_16, times1_16, magnitude1_16 = stft(data_list1, nperseg=window_size, noverlap=overlap_samples)# 设置STFT参数
window_size = 16 # 窗口大小
overlap = 0.5 # 重叠比例
# 计算重叠的样本数
overlap_samples = int(window_size * overlap)
frequencies2_16, times2_16, magnitude2_16 = stft(data_list2, nperseg=window_size, noverlap=overlap_samples)# 设置STFT参数
window_size = 16 # 窗口大小
overlap = 0.5 # 重叠比例
# 计算重叠的样本数
overlap_samples = int(window_size * overlap)
frequencies3_16, times3_16, magnitude3_16 = stft(data_list3, nperseg=window_size, noverlap=overlap_samples)# 设置STFT参数
window_size = 16 # 窗口大小
overlap = 0.5 # 重叠比例
# 计算重叠的样本数
overlap_samples = int(window_size * overlap)
frequencies4_16, times4_16, magnitude4_16 = stft(data_list4, nperseg=window_size, noverlap=overlap_samples)⑥时频矩阵:将所有帧的FFT结果按时间顺序排列,形成时频矩阵,便于后续分析和可视化。
#用 plt.pcolormesh 把 STFT 的结果画出来,横坐标是时间,纵坐标是频率,颜色代表能量大小。
plt.figure(figsize=(20,10), dpi=100)
plt.subplot(2,2,1)
plt.pcolormesh(times1, frequencies1, np.abs(magnitude1), shading='gouraud')
plt.title('尺度 16-内圈')
plt.subplot(2,2,2)
plt.pcolormesh(times2, frequencies2, np.abs(magnitude2), shading='gouraud')
plt.title('尺度 32-内圈')
plt.subplot(2,2,3)
plt.pcolormesh(times3, frequencies3, np.abs(magnitude3), shading='gouraud')
plt.title('尺度 64-内圈')
plt.subplot(2,2,4)
plt.pcolormesh(times4, frequencies4, np.abs(magnitude4), shading='gouraud')
plt.title('尺度 128-内圈')
plt.show()
下面我们可以从原始轴承信号中分别取 2048 点 和 512 点,用于后续对比长窗口和短窗口的效果。
import numpy as np
from scipy.signal import stft
import matplotlib.pyplot as plt# 加载轴承数据集
# 划窗取值
data_list1_max = data_list1[0:2048]
data_list2_max = data_list2[0:2048]
data_list3_max = data_list3[0:2048]
data_list4_max = data_list4[0:2048]data_list1_min = data_list1[0:512]
data_list2_min = data_list2[0:512]
data_list3_min = data_list3[0:512]
data_list4_min = data_list4[0:512]# 计算STFT
# 设置STFT参数
window_size = 128 # 窗口大小
overlap = 0.5 # 重叠比例
# 计算重叠的样本数
overlap_samples = int(window_size * overlap)
frequencies1, times1, magnitude1 = stft(data_list1_max, nperseg=window_size, noverlap=overlap_samples)
overlap_samples = int(window_size * overlap)
frequencies2, times2, magnitude2 = stft(data_list2_max, nperseg=window_size, noverlap=overlap_samples)
overlap_samples = int(window_size * overlap)
frequencies3, times3, magnitude3 = stft(data_list3_max, nperseg=window_size, noverlap=overlap_samples)
overlap_samples = int(window_size * overlap)
frequencies4, times4, magnitude4 = stft(data_list4_max, nperseg=window_size, noverlap=overlap_samples)overlap_samples = int(window_size * overlap)
frequencies5, times5, magnitude5 = stft(data_list1_min, nperseg=window_size, noverlap=overlap_samples)
overlap_samples = int(window_size * overlap)
frequencies6, times6, magnitude6 = stft(data_list2_min, nperseg=window_size, noverlap=overlap_samples)
overlap_samples = int(window_size * overlap)
frequencies7, times7, magnitude7 = stft(data_list3_min, nperseg=window_size, noverlap=overlap_samples)
overlap_samples = int(window_size * overlap)
frequencies8, times8, magnitude8 = stft(data_list4_min, nperseg=window_size, noverlap=overlap_samples)import numpy as np
from scipy.signal import stft
import matplotlib.pyplot as plt# 计算STFT
# 设置STFT参数
window_size = 128 # 窗口大小
overlap = 0.5 # 重叠比例
# 计算重叠的样本数
overlap_samples = int(window_size * overlap)
frequencies1, times1, magnitude1 = stft(data_list1_max, nperseg=window_size, noverlap=overlap_samples)
overlap_samples = int(window_size * overlap)
frequencies2, times2, magnitude2 = stft(data_list2_max, nperseg=window_size, noverlap=overlap_samples)
overlap_samples = int(window_size * overlap)
frequencies3, times3, magnitude3 = stft(data_list3_max, nperseg=window_size, noverlap=overlap_samples)
overlap_samples = int(window_size * overlap)
frequencies4, times4, magnitude4 = stft(data_list4_max, nperseg=window_size, noverlap=overlap_samples)overlap_samples = int(window_size * overlap)
frequencies5, times5, magnitude5 = stft(data_list1_min, nperseg=window_size, noverlap=overlap_samples)
overlap_samples = int(window_size * overlap)
frequencies6, times6, magnitude6 = stft(data_list2_min, nperseg=window_size, noverlap=overlap_samples)
overlap_samples = int(window_size * overlap)
frequencies7, times7, magnitude7 = stft(data_list3_min, nperseg=window_size, noverlap=overlap_samples)
overlap_samples = int(window_size * overlap)
frequencies8, times8, magnitude8 = stft(data_list4_min, nperseg=window_size, noverlap=overlap_samples)plt.figure(figsize=(20,10))
# 用 plt.pcolormesh 把 STFT 的结果画出来,横坐标是时间,纵坐标是频率,颜色代表能量大小。
plt.subplot(2,4,1)
plt.pcolormesh(times1, frequencies1, np.abs(magnitude1), shading='gouraud')
plt.title('正常-2048')
plt.subplot(2,4,2)
plt.pcolormesh(times2, frequencies2, np.abs(magnitude2), shading='gouraud')
plt.title('内圈-2048')
plt.subplot(2,4,3)
plt.pcolormesh(times3, frequencies3, np.abs(magnitude3), shading='gouraud')
plt.title('滚珠-2048')
plt.subplot(2,4,4)
plt.pcolormesh(times4, frequencies4, np.abs(magnitude4), shading='gouraud')
plt.title('外圈-2048')plt.subplot(2,4,5)
plt.pcolormesh(times5, frequencies5, np.abs(magnitude5), shading='gouraud')
plt.title('正常-512')
plt.subplot(2,4,6)
plt.pcolormesh(times6, frequencies6, np.abs(magnitude6), shading='gouraud')
plt.title('内圈-512')
plt.subplot(2,4,7)
plt.pcolormesh(times7, frequencies7, np.abs(magnitude7), shading='gouraud')
plt.title('滚珠-512')
plt.subplot(2,4,8)
plt.pcolormesh(times8, frequencies8, np.abs(magnitude8), shading='gouraud')
plt.title('外圈-512')
plt.show()
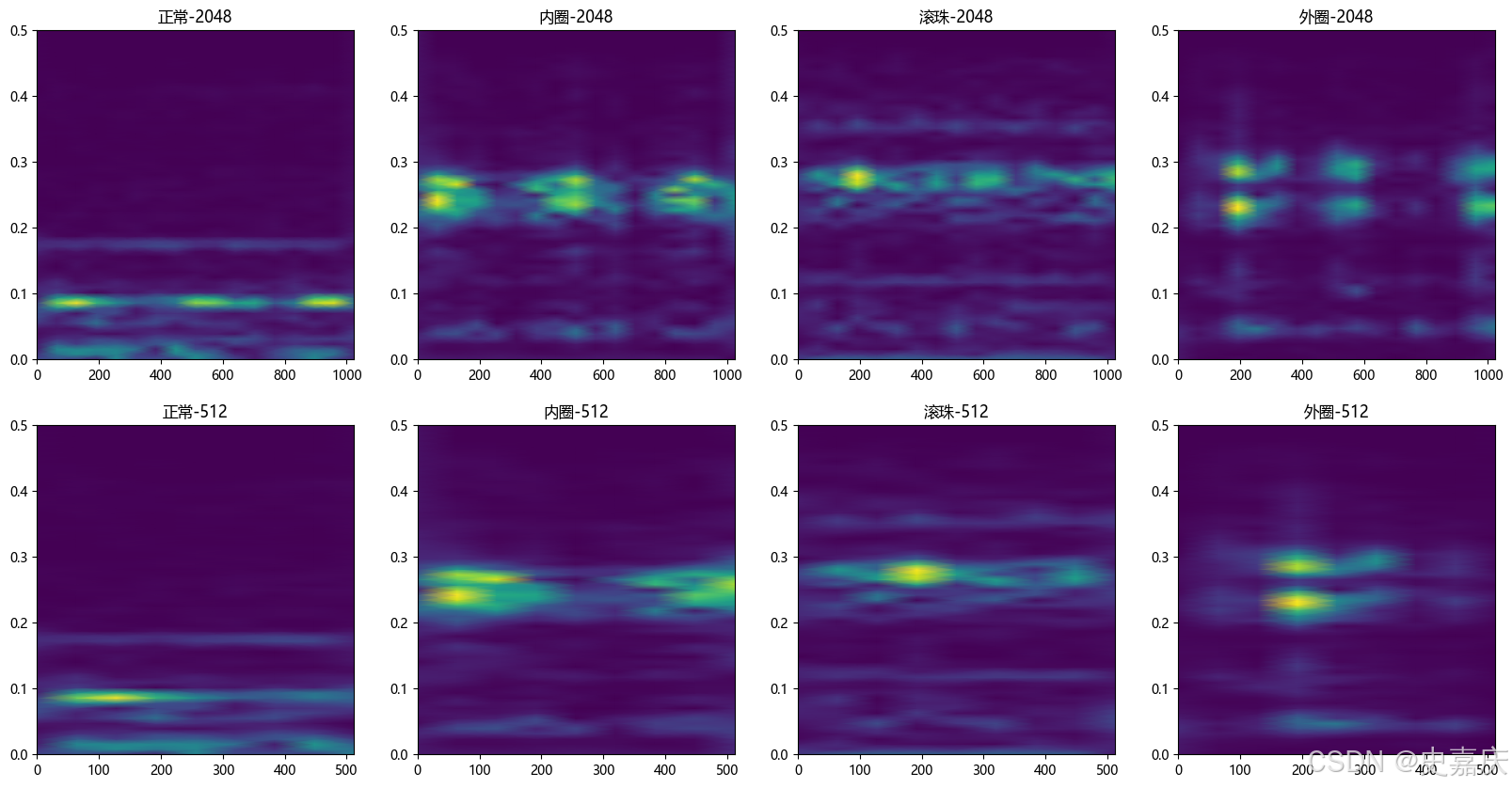
| 工况 | 频率特征 | 时间特征 | 2048 窗(高频率分辨率) | 512 窗(高时间分辨率) |
|---|---|---|---|---|
| 正常 | 能量集中在低频(约 0.1 左右),分布平稳 | 时间上无明显冲击 | 频率分量清晰、单一 | 低频能量带平滑、稳定 |
| 内圈故障 | 出现周期性脉冲频率分量,中低频能量增强 | 有规律重复冲击 | 可分辨出多条频率带,对应周期性故障特征 | 冲击在时间轴上更明显,呈条带状 |
| 滚珠故障 | 能量集中在中频(约 0.25–0.35),孤立点强烈 | 瞬态冲击较突出,但间隔不规则 | 中频频带较清晰,可定位滚珠故障频率 | 时间上能清楚看到孤立的高能点 |
| 外圈故障 | 频率分布最复杂,多个能量峰出现 | 冲击强烈且固定在特定位置反复出现 | 频率分量多且杂乱,能量区分明显 | 时间上呈现出多个不规则强冲击点 |
还有一些其他的方式,不过多介绍。
- 小波变换
- 希尔伯特-黄变换
图像编码方法
这是一些偏数学的方法,格兰姆角场和马尔科夫转移场较为常用,主要介绍前者。
| 方法名称 | 原理描述 |
|---|---|
| 格兰姆角场 | 通过空间变换来消除时间序列噪声;采用向量内积来保存时间信息。 |
| 马尔可夫转移场 | 将时间顺序看成是马尔可夫过程;分成Q个分位箱,构造马尔可夫转移矩阵,生成马尔可夫转移场。 |
| 递归图 | 将时域空间变换为相空间,即每个点变换成相空间中的对应状态;计算状态之间的距离,从而得到相应的图像特征。 |
| 图形差分法 | 通过截取图形不同长度,进行差分等处理,构造图形差分场;保留序列熵(复杂性测量、动态系统特征)。 |
| 相对位置矩阵 | 先进行z-分值标准化,采用PAA进行降维,计算每两个时间戳之间的相对大小关系,最后转换为灰度值矩阵。 |
格兰姆角场
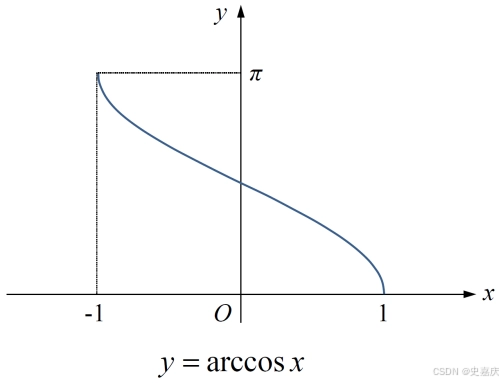
1.时间序列归一化:将原始时间序列的值缩放到一个固定的区间(通常是[-1,1]或[0,1]),这对于后续的角度计算至关重要,因为反余弦函数的定义域是[-1,1]
2.极坐标转换:将归一化后的时间序列点从笛卡尔坐标系(索引,值)转换到极坐标系(半径,角度),最后每个原始时间点(i,xi)(i,x_i)(i,xi)在极坐标中表示为(ri,pi)(r_i,p_i)(ri,pi)。
半径rir_iri:通过设置为时间戳的归一化值。最简单的方式是线性映射时间索引到 [0,1][0,1][0,1]区间,其中 nnn 是序列长度。半径编码了时间顺序。
ri=in−1r_i = \frac{i}{n - 1} ri=n−1i
角度φi\varphi_iφi:将归一化值xix_ixi 直接映射为角度,其中 0≤φi≤π0 \leq \varphi_i \leq \pi0≤φi≤π
φi=arccos(xi)\varphi_i = \arccos(x_i)φi=arccos(xi)
3.计算格兰姆角场矩阵(GASF和GADF):创建一个 n×nn \times nn×n 的矩阵 GGG,其元素 GijG_{ij}Gij 编码了点和点的角度信息以及它们的时间关系(通过半径隐含,即时间索引 iii 和 jjj 在矩阵中的位置定义了 GijG_{ij}Gij 所代表的时间点对 (i,j)(i,j)(i,j) 的关系)。
GASF格兰姆和角场:
Gij=cos(φi+φj)G_{ij} = \cos(\varphi_i + \varphi_j)Gij=cos(φi+φj) Gij=cos(φi+φj)=cos(φi)cos(φj)−sin(φi)sin(φj)G_{ij} = \cos(\varphi_i + \varphi_j) = \cos(\varphi_i)\cos(\varphi_j) - \sin(\varphi_i)\sin(\varphi_j) Gij=cos(φi+φj)=cos(φi)cos(φj)−sin(φi)sin(φj)
由 φi=arccos(xi)\varphi_i = \arccos(x_i)φi=arccos(xi),可得 cos(φi)=xi\cos(\varphi_i) = x_icos(φi)=xi
由三角恒等式 sin(φi)=1−cos2(φi)=1−xi2\sin(\varphi_i) = \sqrt{1-\cos^2(\varphi_i)} = \sqrt{1-x_i^2}sin(φi)=1−cos2(φi)=1−xi2
Gij=xixj−(1−xi2)(1−xj2)G_{ij} = x_i x_j - \sqrt{(1-x_i^2)(1-x_j^2)} Gij=xixj−(1−xi2)(1−xj2)
GADF格兰姆差角场: Gij=sin(φi−φj)G_{ij} = \sin(\varphi_i - \varphi_j)Gij=sin(φi−φj)
当然这个方法实际上python已经封装好了,在官方文档库中有下面这样一个例子:
# Author: Johann Faouzi <johann.faouzi@gmail.com> # 作者与邮箱
# License: BSD-3-Clause # 许可协议import numpy as np # 导入数值计算库 NumPy
import matplotlib.pyplot as plt # 导入绘图库 Matplotlib
from pyts.image import GramianAngularField # 从 pyts.image 模块导入 GramianAngularField 类# ---------------------------
# 1. 生成一个时间序列
# ---------------------------
time_points = np.linspace(0, 4 * np.pi, 1000) # 在线性区间 [0, 4π] 上取 1000 个时间点
x = np.sin(time_points) # 计算正弦函数,得到时间序列 x(t) = sin(t)
X = np.array([x]) # 将一维序列包装成二维数组,形状为 (1, 1000)# ---------------------------
# 2. 计算 Gramian Angular Fields
# ---------------------------
# 核心代码只有这两行:method指定是和角场还是差角场
gasf = GramianAngularField(method='summation') # 创建 GAF 对象,使用求和(Summation)模式
X_gasf = gasf.fit_transform(X) # 计算 Gramian Angular Summation Field,返回形状 (1, 1000, 1000)gadf = GramianAngularField(method='difference') # 创建 GAF 对象,使用差分(Difference)模式
X_gadf = gadf.fit_transform(X) # 计算 Gramian Angular Difference Field# ---------------------------
# 3. 设置画布与网格布局
# ---------------------------
width_ratios = (2, 7, 7, 0.4) # 网格列宽比例:左侧 2,两个主图各 7,右侧色条 0.4
height_ratios = (2, 7) # 网格行高比例:上 2,下 7
width = 10 # 图像整体宽度
height = width * sum(height_ratios) / sum(width_ratios) # 根据比例计算高度保持长宽比
fig = plt.figure(figsize=(width, height)) # 创建画布
gs = fig.add_gridspec(2, 4, # 创建 2x4 网格width_ratios=width_ratios,height_ratios=height_ratios,left=0.1, right=0.9, bottom=0.1, top=0.9, # 留白设置wspace=0.1, hspace=0.1) # 网格间距# ---------------------------
# 4. 定义坐标轴刻度与标签
# ---------------------------
time_ticks = np.linspace(0, 4 * np.pi, 9) # 时间刻度 9 个点
time_ticklabels = [r'$0$', r'$\frac{\pi}{2}$', r'$\pi$', # LaTeX 形式的时间刻度标签r'$\frac{3\pi}{2}$', r'$2\pi$', r'$\frac{5\pi}{2}$',r'$3\pi$', r'$\frac{7\pi}{2}$', r'$4\pi$']
value_ticks = [-1, 0, 1] # y 轴数值刻度(幅度)
reversed_value_ticks = value_ticks[::-1] # 反转列表,用于左侧倒置 x 轴# ---------------------------
# 5. 左侧:倒置坐标展示时间序列
# ---------------------------
ax_left = fig.add_subplot(gs[1, 0]) # 左下角子图
ax_left.plot(x, time_points) # 横轴幅值 x,纵轴时间 t,得到垂直的时序图
ax_left.set_xticks(reversed_value_ticks) # 设置横轴刻度
ax_left.set_xticklabels(reversed_value_ticks, rotation=90) # 刻度标签竖排显示
ax_left.set_yticks(time_ticks) # 设置纵轴刻度
ax_left.set_yticklabels(time_ticklabels, rotation=90) # 纵轴标签竖排显示
ax_left.set_ylim((0, 4 * np.pi)) # 设置纵轴范围
ax_left.invert_xaxis() # 反转横轴,使 -1 在右,+1 在左# ---------------------------
# 6. 上方:水平放置时间序列(两次,便于与两幅 GAF 对应)
# ---------------------------
ax_top1 = fig.add_subplot(gs[0, 1]) # 上方第一幅
ax_top2 = fig.add_subplot(gs[0, 2]) # 上方第二幅
for ax in (ax_top1, ax_top2): # 循环设置两个坐标轴ax.plot(time_points, x) # 绘制时间序列ax.set_xticks(time_ticks) # 设置横轴刻度ax.set_xticklabels(time_ticklabels) # 使用 LaTeX 标签ax.set_yticks(value_ticks) # 设置纵轴刻度ax.xaxis.tick_top() # 将横轴刻度移到顶部ax.set_xlim((0, 4 * np.pi)) # 设置横轴范围
ax_top1.set_yticklabels(value_ticks) # 左侧图显示纵轴标签
ax_top2.set_yticklabels([]) # 右侧图不显示纵轴标签# ---------------------------
# 7. 下方中间两幅:显示 GAF 图像
# ---------------------------
ax_gasf = fig.add_subplot(gs[1, 1]) # 左下中:Summation GAF
ax_gasf.imshow(X_gasf[0], cmap='rainbow', origin='lower', # 显示图像,使用彩虹色图extent=[0, 4 * np.pi, 0, 4 * np.pi]) # 设置坐标轴范围
ax_gasf.set_xticks([]) # 隐藏刻度
ax_gasf.set_yticks([])
ax_gasf.set_title('Gramian Angular Summation Field', y=-0.09) # 标题下移一点ax_gadf = fig.add_subplot(gs[1, 2]) # 右下中:Difference GAF
im = ax_gadf.imshow(X_gadf[0], cmap='rainbow', origin='lower',extent=[0, 4 * np.pi, 0, 4 * np.pi])
ax_gadf.set_xticks([])
ax_gadf.set_yticks([])
ax_gadf.set_title('Gramian Angular Difference Field', y=-0.09)# ---------------------------
# 8. 右侧:添加颜色条
# ---------------------------
ax_cbar = fig.add_subplot(gs[1, 3]) # 右下侧色条子图
fig.colorbar(im, cax=ax_cbar) # 将 ax_gadf 最后的图像 im 作为颜色条参考
plt.show() # 显示所有图形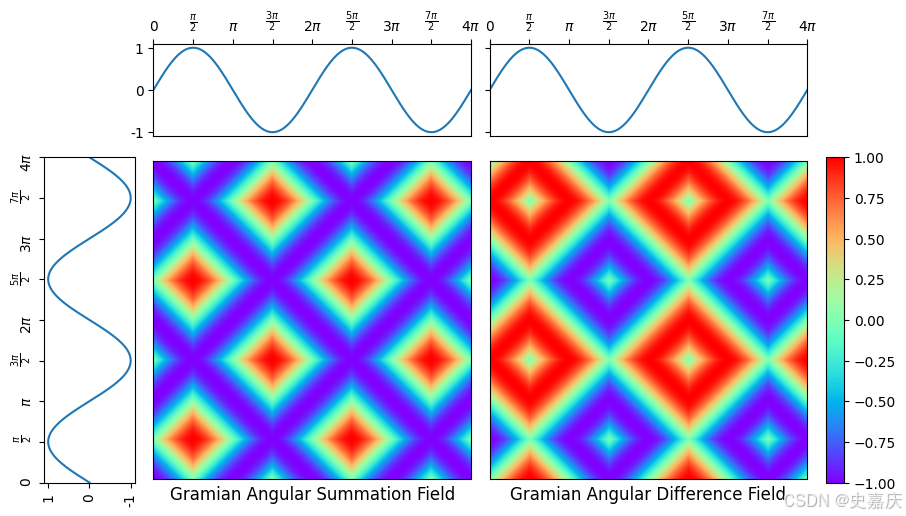
经过封装的方法处理后,上述时序数据就被转换为了一张图片,可以送到对应的网络结构进行下一步的分析,这也是重要的时序数据特征提取的方式。
短时傅里叶变换 VS 格兰姆角场
| 对比维度 | 短时傅里叶变换 | 格兰姆角场 |
|---|---|---|
| 核心原理 | 滑动窗口+FFT,进行局部频谱分析 | 极坐标编码+内积,捕获时序依赖关系 |
| 输出形式 | 2D矩阵:[时间帧,频率] | 2D方阵:[时间,时间] |
| 关键优势 | 直观展示频率随时间变化 适合振荡、非平稳信号 | 保留全局时序结构与依赖 对幅度缩放不敏感,适合数值序列 |
| 主要局限 | 时频分辨率不可兼得 窗口间依赖关系弱 | 计算复杂度高 物理意义不如STFT直观 |
