使用 BayesFlow 神经网络简化贝叶斯推断的案例分享（二）

继续【使用 BayesFlow 通过神经网络简化贝叶斯推断（一）】

1 BayesFlow启动指南

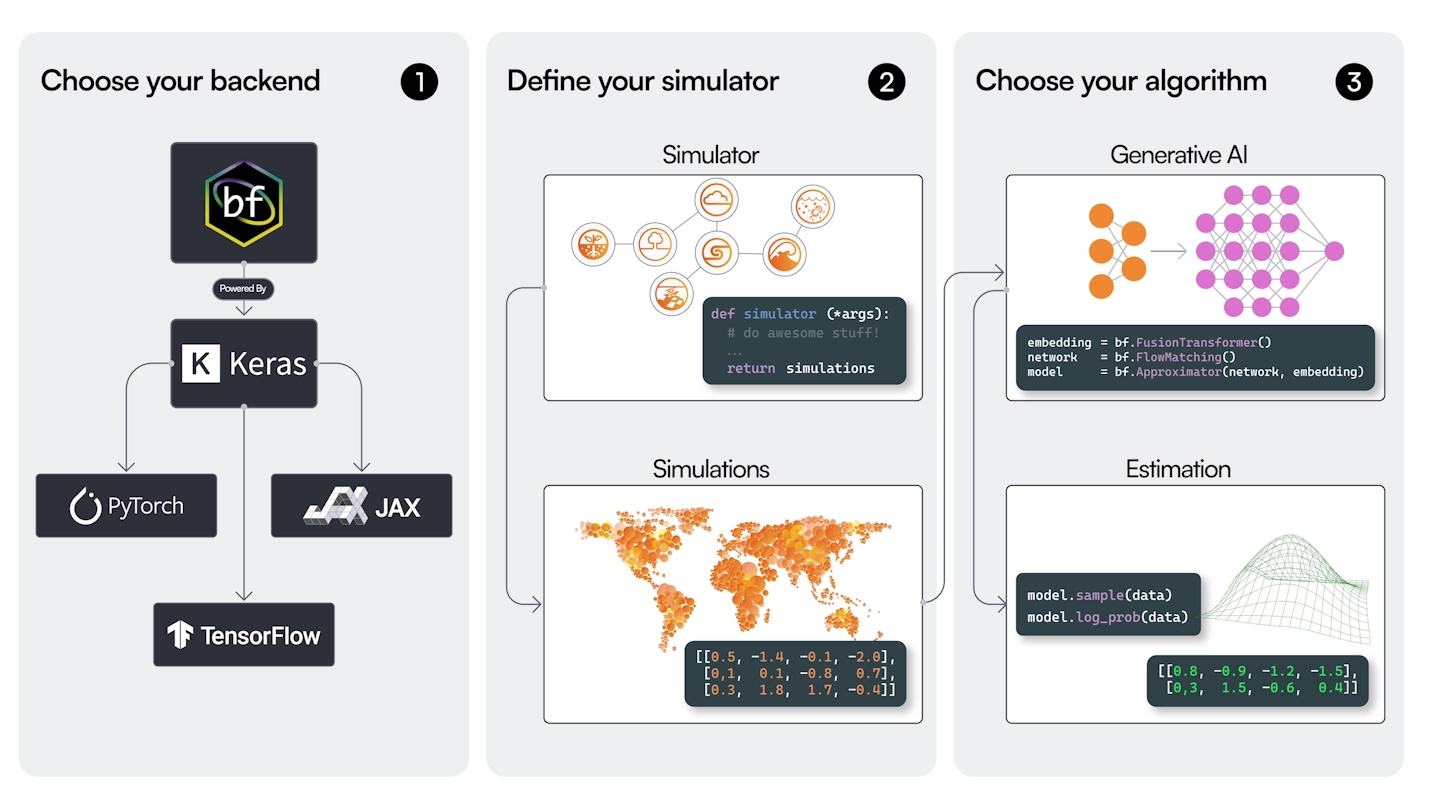
BayesFlow 是一个用于摊销贝叶斯推断的 Python 库，采用神经网络实现。不同于为每个新数据集从头计算后验，BayesFlow 学习一个神经网络，能够即时为任何观测数据近似后验。这种"摊销"方法将计算成本分摊到多个推断任务中，非常适合需要重复执行贝叶斯推断的场景。

该库通过 Keras3 支持多个后端（PyTorch、TensorFlow、JAX），让您可以灵活选择深度学习框架。

1.1 安装与设置

首先安装 BayesFlow 并选择您偏好的后端：

pip install "bayesflow>=2.0"

您还需要安装以下后端之一：

• JAX（推荐以获得最佳性能）
• PyTorch
• TensorFlow

在 Python 中设置后端：

import os
os.environ["KERAS_BACKEND"] = "jax"  # 或 "torch" 或 "tensorflow"
import bayesflow as bf

让我们使用双月示例创建一个完整的 BayesFlow 工作流程。这是一个基于模拟推断的基准问题，其后验分布呈现独特的双月形状。

1.1.1 第 1 步：定义模拟器

模拟器代表您的数据生成过程。它包含两部分：参数的先验分布和从参数生成数据的前向模型。

import numpy as npdef theta_prior():"""定义参数的先验分布"""theta = np.random.uniform(-1, 1, 2)return dict(theta=theta)def forward_model(theta):"""定义从参数生成数据的前向模型"""alpha = np.random.uniform(-np.pi / 2, np.pi / 2)r = np.random.normal(0.1, 0.01)x1 = -np.abs(theta[0] + theta[1]) / np.sqrt(2) + r * np.cos(alpha) + 0.25x2 = (-theta[0] + theta[1]) / np.sqrt(2) + r * np.sin(alpha)return dict(x=np.array([x1, x2]))# 组合成单个模拟器
simulator = bf.make_simulator([theta_prior, forward_model])

1.1.2 第 2 步：创建适配器

适配器将模拟器输出转换为神经网络期望的格式。它处理数据类型转换、数组变换和变量重命名。

adapter = (bf.adapters.Adapter().to_array()                    # 转换为 numpy 数组.convert_dtype("float64", "float32")  # 深度学习使用 float32.rename("theta", "inference_variables")  # 为网络输入重命名.rename("x", "inference_conditions")    # 为条件重命名
)

1.1.3 第 3 步：选择神经网络

BayesFlow 为不同的推断任务提供各种神经网络架构。本示例中，我们将使用流匹配（Flow Matching），它适用于多模态后验。

inference_network = bf.networks.FlowMatching(subnet="mlp", subnet_kwargs={"dropout": 0.0, "widths": (256,)*6}
)

1.1.4 第 4 步：创建工作流程

工作流程将所有组件整合在一起：模拟器、适配器和神经网络。它为训练和推断提供高级接口。

workflow = bf.BasicWorkflow(simulator=simulator,adapter=adapter,inference_network=inference_network,
)

1.1.5 第 5 步：训练模型

生成训练数据并训练网络。在这个快速示例中，我们将使用小数据集进行离线训练。

# 生成训练数据
num_training_batches = 512
batch_size = 64
epochs = 50training_data = simulator.sample(num_training_batches * batch_size)
validation_data = simulator.sample(300)# 训练模型
history = workflow.fit_offline(data=training_data,epochs=epochs,batch_size=batch_size,validation_data=validation_data
)

1.1.6 第 6 步：执行推断

训练完成后，您可以使用工作流程即时为新观测值近似后验：

# 定义新观测值
conditions = {"x": np.array([[0.0, 0.0]]).astype("float32")}# 从后验采样
num_samples = 1000
posterior_samples = workflow.sample(conditions=conditions, num_samples=num_samples)# 结果是包含参数样本的字典
print(f"后验样本形状: {posterior_samples['theta'].shape}")

1.2 理解工作流程

让我们可视化完整的 BayesFlow 工作流程：

• 先验分布
• 前向模型
• 模拟器
• 适配器
• 神经网络
• 训练好的近似器
• 新数据
• 即时后验样本

工作流程遵循以下关键步骤：

1. 模拟器：将您的先验知识和前向模型组合成单个数据生成过程
2. 适配器：将原始模拟器输出转换为神经网络友好格式
3. 神经网络：学习近似从数据到后验分布的映射
4. 训练：网络在模拟数据上训练以摊销推断成本
5. 推断：训练完成后，网络为新数据提供即时后验近似

1.3 接下来做什么？

以下是一些建议的后续步骤：

• 尝试不同架构：实验使用 bf.networks.CouplingFlow() 或 bf.networks.ConsistencyModel()
• 使用在线训练：为获得更好性能，尝试 workflow.fit_online() 替代离线训练
• 探索诊断：使用 workflow.plot_default_diagnostics() 验证结果
• 查看更多示例：参考[线性回归]

1.4 关键要点

• BayesFlow 实现摊销贝叶斯推断 - 一次学习，即时推断
• 该库提供模块化工作流程，包含模拟器、适配器、网络和工作流程
• 您可以切换后端（JAX、PyTorch、TensorFlow）而只需少量代码更改
• 训练在模拟数据上进行，非常适合具有难处理似然的模型
• 训练完成后，推断极其快速 - 非常适合实时应用

2 简单案例：使用BayesFlow进行线性回归

具体可以参考：Linear_Regression_Starter.ipynb

线性回归是一种基础的统计模型，构成了许多机器学习应用的支柱。在本教程中，我们将探讨如何使用BayesFlow（一个强大的摊销贝叶斯推断库）来实现贝叶斯线性回归。您将学习如何利用神经网络高效地近似后验分布，即使对于不同大小的数据集也能实现快速推断。

2.1 传统的贝叶斯线性回归推断

传统的贝叶斯线性回归推断需要为每个数据集计算新的后验分布，这在计算上可能非常昂贵，特别是在处理多个数据集或不同样本量时。BayesFlow通过摊销推断解决这个问题——训练一次神经网络来近似同一模型族中任何数据集的后验分布。

可以将其理解为学习一个将数据映射到后验分布的通用函数，而不是从头开始解决每个推断问题。当您需要在具有不同特性的多个数据集上执行推断时，这种方法特别强大。

2.2 设置生成模型

在BayesFlow中，我们通过三个关键组件来定义统计模型：

2.2.1 似然函数

似然函数根据给定参数生成数据。对于线性回归，我们模拟预测变量x和响应变量y：

def likelihood(beta, sigma, N):# x: 预测变量x = np.random.normal(0, 1, size=N)# y: 响应变量y = np.random.normal(beta[0] + beta[1] * x, sigma, size=N)return dict(y=y, x=x)

该函数接受回归系数beta（截距和斜率）、残差标准差sigma和观测值数量N。它返回预测变量和响应变量。

2.2.2. 先验分布

先验分布编码了我们在观测数据前对参数的信念：

def prior():# beta: 回归系数（截距、斜率）beta = np.random.normal([2, 0], [3, 1])# sigma: 残差标准差sigma = np.random.gamma(1, 1)return dict(beta=beta, sigma=sigma)

我们使用正态分布作为回归系数的先验，使用伽马分布作为正残差标准差的先验。

2.2.3. 元模拟器

为了处理不同大小的数据集，我们定义一个元模拟器来采样观测值数量：

def meta():# N: 数据集中的观测值数量N = np.random.randint(5, 15)return dict(N=N)

这使得我们的模型能够处理不同大小的数据集，使其在实际应用中更加灵活。

2.2.4 创建模拟器

我们将这些组件组合成一个BayesFlow模拟器：

simulator = bf.simulators.make_simulator([prior, likelihood], meta_fn=meta)

模拟器可以生成带有相应参数的数据集批次，从而实现神经网络近似器的高效训练。

2.3 使用适配器进行数据预处理

在将数据输入神经网络之前，我们需要使用BayesFlow的适配器系统对其进行预处理：

adapter = (bf.Adapter().broadcast("N", to="x").as_set(["x", "y"]).constrain("sigma", lower=0).sqrt("N").convert_dtype("float64", "float32").concatenate(["beta", "sigma"], into="inference_variables").concatenate(["x", "y"], into="summary_variables").rename("N", "inference_conditions")
)

让我们分解每个转换的作用：

• broadcast: 将标量N复制以匹配批次维度
• as_set: 将x和y视为可交换的（顺序无关）
• constrain: 确保sigma保持正值
• sqrt: 对N应用平方根变换
• convert_dtype: 转换数据类型以兼容神经网络
• concatenate: 将变量组合到适当的组中
• rename: 重命名变量以提高清晰度

2.4 构建神经网络架构

BayesFlow使用两部分神经网络架构进行摊销推断：

2.4.1 摘要网络

摘要网络将可变大小的数据处理为固定长度表示：

summary_network = bf.networks.SetTransformer(summary_dim=10)

SetTransformer是置换不变的，意味着它将观测值视为可交换的——数据点的顺序不会影响学习到的表示。这对于许多统计模型至关重要，在这些模型中观测值的顺序不应该影响结果。

2.4.2 推断网络

推断网络学习将数据摘要映射到后验分布：

inference_network = bf.networks.CouplingFlow(transform="spline")

我们使用带有样条变换的耦合流，这在建模复杂后验分布时提供了灵活性，同时保持了可计算性。

2.4.3 创建工作流

我们将这些组件组合成一个处理训练和推断的工作流：

workflow = bf.BasicWorkflow(simulator=simulator,adapter=adapter,inference_network=inference_network,summary_network=summary_network,standardize=["inference_variables", "summary_variables"]
)

工作流协调整个过程，从数据生成到训练和推断。

2.5 训练近似器

使用fit_online方法进行训练非常简单：

history = workflow.fit_online(epochs=50, batch_size=64, num_batches_per_epoch=200)

这通过以下方式训练神经网络来近似后验分布：

1. 生成模拟数据集批次
2. 通过适配器处理它们
3. 计算真实后验和近似后验之间的损失
4. 通过反向传播更新网络权重

在标准笔记本电脑上，训练过程通常需要2-5分钟。您可以通过绘制损失曲线来监控进度：

f = bf.diagnostics.plots.loss(history)

2.6 执行推断

一旦训练完成，我们可以使用近似器进行快速后验推断：

# 模拟验证数据
val_sims = simulator.sample(200)# 获取后验样本
post_draws = workflow.sample(conditions=val_sims, num_samples=1000)

这为200个验证数据集中的每一个生成1000个后验样本，所需时间只是传统MCMC方法的一小部分。

2.7 评估结果

BayesFlow提供全面的诊断工具来评估后验近似的质量：

2.7.1 恢复分析

检查真实参数值是否被后验分布覆盖：

f = bf.diagnostics.plots.recovery(estimates=post_draws, targets=val_sims,variable_names=par_names
)

这创建散点图，显示真实参数值与后验均值/中位数之间的关系。

2.7.2 基于模拟的校准

评估您的近似后验是否在统计上经过校准：

f = bf.diagnostics.plots.calibration_ecdf(estimates=post_draws, targets=val_sims,variable_names=par_names,difference=True,rank_type="distance"
)

校准图有助于确保您的后验近似具有正确的覆盖特性。

2.7.3 自定义检验量

您还可以定义自定义检验量以进行更详细的诊断：

def joint_log_likelihood(data):beta = data["beta"]sigma = data["sigma"]x = data["x"]y = data["y"]mean = beta[:,0][:,None] + beta[:,1][:,None] * xlog_lik = np.sum(- (y - mean)**2 / (2 * sigma**2) - 0.5 * np.log(2 * np.pi) - np.log(sigma), axis=-1)return log_lik

这允许您检查数据相关量（如联合对数似然）的校准情况。

2.7.4 后验收缩分析

检查后验从数据中学到了多少：

f = bf.diagnostics.plots.z_score_contraction(estimates=post_draws, targets=val_sims,variable_keys=["beta"],variable_names=par_names[0:2]
)

这有助于您理解从先验到后验的信息增益。

2.7.5 保存和加载模型

BayesFlow使保存和重新加载训练好的近似器变得简单：

# 保存模型
filepath = Path("checkpoints") / "regression.keras"
filepath.parent.mkdir(exist_ok=True)
workflow.approximator.save(filepath=filepath)# 加载模型
approximator = keras.saving.load_model(filepath)

所有方法在加载的近似器上继续有效，支持在生产环境中无缝部署。

3 双月问题：处理双峰后验

作者：Lars Kühmichel, Marvin Schmitt, Valentin Pratz, Stefan T. Radev

import os# Set to your favorite backendif "KERAS_BACKEND" not in os.environ:# set this to "torch", "tensorflow", or "jax"os.environ["KERAS_BACKEND"] = "jax"else:print(f"Using '{os.environ['KERAS_BACKEND']}' backend")
import numpy as npimport matplotlib.pyplot as pltimport seaborn as snsimport bayesflow as bf

3.1 模拟器

def theta_prior():theta = np.random.uniform(-1, 1, 2)return dict(theta=theta)def forward_model(theta):alpha = np.random.uniform(-np.pi / 2, np.pi / 2)r = np.random.normal(0.1, 0.01)x1 = -np.abs(theta[0] + theta[1]) / np.sqrt(2) + r * np.cos(alpha) + 0.25x2 = (-theta[0] + theta[1]) / np.sqrt(2) + r * np.sin(alpha)return dict(x=np.array([x1, x2]))

simulator = bf.make_simulator([theta_prior, forward_model])

# generate 3 random draws from the joint distribution p(r, alpha, theta, x)sample_data = simulator.sample(3)
print("Type of sample_data:\n\t", type(sample_data))print("Keys of sample_data:\n\t", sample_data.keys())print("Types of sample_data values:\n\t", {k: type(v) for k, v in sample_data.items()})print("Shapes of sample_data values:\n\t", {k: v.shape for k, v in sample_data.items()})

3.2 适配器

下一步是告诉 BayesFlow 如何处理所有模拟变量。你也可以把这看作告知 BayesFlow 数据流，即哪些变量传入哪些网络，以及在把模拟器输出传入网络之前需要执行哪些变换。这通过适配器层来完成，适配器实现为一系列固定的、伪可逆的数据变换。

下面我们通过指定输入/输出键和要应用的变换来定义数据适配器。这允许我们完全控制数据流。

adapter = (bf.adapters.Adapter()# convert any non-arrays to numpy arrays.to_array()# convert from numpy's default float64 to deep learning friendly float32.convert_dtype("float64", "float32")# rename the variables to match the required approximator inputs.rename("theta", "inference_variables").rename("x", "inference_conditions"))adapter

3.3 数据集

在本例中，我们会预先采样训练数据并使用离线训练（offline training）并设置较少的训练轮数。在实际应用中，通常需要更长时间训练以获得最佳性能。

num_training_batches = 512num_validation_sets = 300batch_size = 64epochs = 50
training_data = simulator.sample(num_training_batches * batch_size)validation_data = simulator.sample(num_validation_sets)

3.4 训练用于逼近所有后验的神经网络

下一步是搭建用于逼近后验 p(θ | x) 的神经网络。

我们选择 Flow Matching [1, 2] 作为本示例的主干架构，因为它能较好地处理某些观测量所导致的多模态后验。

• [1] Lipman, Y., Chen, R. T., Ben-Hamu, H., Nickel, M., & Le, M. Flow Matching for Generative Modeling. In The Eleventh International Conference on Learning Representations.
• [2] Wildberger, J. B., Dax, M., Buchholz, S., Green, S. R., Macke, J. H., & Schölkopf, B. Flow Matching for Scalable Simulation-Based Inference. In Thirty-seventh Conference on Neural Information Processing Systems.

flow_matching = bf.networks.FlowMatching(subnet="mlp", subnet_kwargs={"dropout": 0.0, "widths": (256,)*6})

该推断网络只是一个通用的 Flow Matching 主干，尚未根据具体的推断任务（即后验近似）进行适配。为实现该适配，我们将网络与数据适配器结合，二者共同构成 approximator。在本例中，我们需要一个 ContinuousApproximator，因为目标是逼近连续参数向量 θ 的后验。

3.4.1 基本工作流

我们可以在 Workflow 对象中封装许多传统深度学习步骤（例如指定学习率和优化器）。该对象把所有内容包裹在一起，并提供一些训练和“理论上”验证的实用函数。

flow_matching_workflow = bf.BasicWorkflow(simulator=simulator,adapter=adapter,inference_network=flow_matching,)

3.4.2 训练

我们现在准备在双月示例上训练后验逼近器。我们使用工具函数 fit_offline，它封装了 approximator 的灵活 fit 方法。

history = flow_matching_workflow.fit_offline(data=training_data, epochs=epochs, batch_size=batch_size, validation_data=validation_data)

3.5 切换推断网络

3.5.1 一致性模型：背景

Consistency Models (CM; [1]) 利用基于 score 的扩散（score-based diffusion）的良好性质来实现少步采样。基于 score 的扩散最初依赖于用于采样的随机微分方程（SDE），但也存在一个常微分方程（ODE），它在每个时间步 t 上具有相同的边际分布 [2]。这意味着尽管 SDE 和 ODE 在噪声分布到目标分布的路径上会产生不同的轨迹，但在某一时间 t 上查看多条路径时得到的分布是一致的。该 ODE 也称为概率流（Probability Flow）ODE。

CM 的目标如下：每个时刻 t 的每个点属于恰好一条路径，我们希望预测这条路径在 t=0 时会落到哪里。实现此功能的函数称为一致性函数 f。如果对所有 t∈(0,T] 都有正确的函数，我们就可以直接从潜在分布（t=T）采样，并用 f 将其直接映射到 t=0，对应目标分布。这样在从目标分布采样时，我们就避免了任何积分，仅需一次对一致性函数的求值。但在实际中，一步采样效果通常不佳，因此我们采用多步采样方法，多次调用 f。更多背景请参见文献 [1]。

当阅读上面内容时，你可能会疑惑为什么我们要学习所有中间时间步 t∈[0,T] 的映射，而不仅仅是 t=T 的映射。主要原因是为了高效训练，我们不想在训练时实际计算与这两点相关的精确积分，这往往代价太高。学习所有时间步为一种不同的训练方法打开了可能性，从而避免在训练时做精确积分。细节较复杂，感兴趣可以查阅 [1]。

训练 首先，我们知道在 t=0 时，f(θ, t=0) = θ，因为 θ 在路径上，它在 t=0 处结束于 θ。这个边界条件作为训练的“锚点”，这是网络在训练开始时已知的信息（我们用一个随时间变化的跳跃连接编码它，使网络在 t=0 时被迫为恒等映射）。在训练时，我们需要把这条信息传递到其余时间段。基本思想是：取一个更靠近数据分布的点 θ1（即较小的时间 t1），并对路径进行一小步 dt 的积分得到 θ2（对应更靠近潜在分布的较大时间 t2 = t1 + dt）。由于对 t=0 我们知道网络在路径上提供正确的输出，我们希望把小时间处的信息向大时间处传播。训练目标是将 f(θ2, t=t2) 的输出向 f(θ1, t=t1) 的输出移动。如何选择 θ1、t1 和 dt 是经验性问题，详见 [1] 的讨论。

蒸馏推断 对于“蒸馏”，我们从一个训练好的 score-based 扩散模型开始。可以用它来积分概率流 ODE，从 θ1 到 θ2。如果没有这样的模型，似乎我们会受阻，因为我们不知道哪些点位于同一路径上，也就不知道应使哪些输出相似。幸运的是，存在一个无偏近似器，如果对许多样本求平均（详见论文），也能给出正确的 score。如果在训练中使用该近似器，并且仅使用单步 Euler 步沿路径移动，我们就得到了一种类似于蒸馏的方法，称为一致性训练（Consistency Training，CT），它允许我们仅使用来自数据分布的样本来训练一致性模型。该算法在 [3] 中得到了显著改进，我们在实现中也包含了这些改进。

改进一致性训练 我们做了若干改进以实现独立的一致性训练算法。因此，引入的超参数及其选择变得有些不直观，需要依赖经验观察和启发式方法。详见 [4]，建议以文中提供的值作为起点。如果你发现明显更好的超参数组合，欢迎告知（例如开 issue 或发邮件），这将帮助他人更快找到合适的超参数区域。

• [1] Song, Y., Dhariwal, P., Chen, M., & Sutskever, I. (2023). Consistency Models. arXiv preprint. https://doi.org/10.48550/arXiv.2303.01469
• [2] Song, Y., Sohl-Dickstein, J., Kingma, D. P., Kumar, A., Ermon, S., & Poole, B. (2021). Score-Based Generative Modeling through Stochastic Differential Equations. ICLR. https://openreview.net/forum?id=PxTIG12RRHS
• [3] Song, Y., & Dhariwal, P. (2023). Improved Techniques for Training Consistency Models. arXiv preprint. https://doi.org/10.48550/arXiv.2310.14189
• [4] Schmitt, M., Pratz, V., Köthe, U., Bürkner, P.-C., & Radev, S. T. (2024). Consistency Models for Scalable and Fast Simulation-Based Inference. arXiv preprint. https://doi.org/10.48550/arXiv.2312.05440

3.5.2 一致性模型：规范说明

现在我们可以定义新推断网络主干。除了一些常规参数（例如学习率和批量大小），一致性模型还有若干相互影响较强的超参数，主要包括：

• 最大时间 max_time：也作为潜在分布的标准差。可尝试 10–200 的取值，应该大于目标分布的标准差。
• 训练期间最小/最大离散步数 s0/s1：作用较难直观理解。通常 s0=10 表现良好。直觉上，增大 s1 并配合更多 epochs 应能提升结果，但在实际中高 s1 有时会导致失败，可能依赖于问题。
• sigma2：修改跳跃连接的时间依赖性。建议保持 1.0 或设为目标分布的近似方差。
• 最小时间 eps（为数值稳定起见用 t=ε 代替 t=0）：只要足够小，影响不大。

你可能会发现不同任务需要调整不同超参数。

关于 dropout 的简短说明：实验中通常会发现 dropout 降低性能，故一般建议将 dropout 设为 0.0。Consistency training 已经利用了一个带噪估计器的 score，因此训练本身已包含足够噪声，额外的 dropout 并非必要。

consistency_model = bf.networks.ConsistencyModel(total_steps=num_training_batches*epochs,subnet_kwargs={"dropout": 0.0, "widths": (256,)*6},max_time=10, # this probably needs to be tuned for a novel applicationsigma2=1.0,  # the approximator standardizes our parameters, so set to 1.0)# Workflow for consistency modelconsistency_model_workflow = bf.BasicWorkflow(simulator=simulator,adapter=adapter,inference_network=consistency_model,)

3.5.3 一致性训练

history = consistency_model_workflow.fit_offline(data=training_data, epochs=epochs, batch_size=batch_size, validation_data=validation_data)

3.6 经典耦合流（Coupling Flows）

当然，BayesFlow 还支持各种参数的耦合流模型，包括传统的仿射（affine）和样条（spline）流。

affine_flow = bf.networks.CouplingFlow(subnet="mlp")affine_flow_workflow = bf.BasicWorkflow(simulator=simulator,adapter=adapter,inference_network=affine_flow,)

我们使用一个更浅的样条耦合流（默认深度为 6）：

# Use a shallower spline coupling flow (default depth is 6)spline_flow = bf.networks.CouplingFlow(subnet="mlp", transform="spline", depth=4)spline_flow_workflow = bf.BasicWorkflow(simulator=simulator,adapter=adapter,inference_network=spline_flow,)

3.6.1 耦合流训练

首先训练经典的仿射耦合流：

history = affine_flow_workflow.fit_offline(data=training_data,epochs=30,batch_size=batch_size,validation_data=validation_data)

接着训练样条流（训练轮数更少）。在多模态、低维问题上，样条流通常优于仿射流。

history = spline_flow_workflow.fit_offline(data=training_data,epochs=30,batch_size=batch_size,validation_data=validation_data)

3.7 验证

3.7.1 双月后验

在点 x = (0, 0) 处的双月后验应呈现两个新月形。下面我们绘制相应的后验样本与后验密度。

这些结果表明这些生成网络能够较好地逼近真实后验。如果使用在线训练、更多 epochs 或更好的优化器超参数，能得到更好的拟合。

# Set the number of posterior draws you want to getnum_samples = 3000# Obtain samples from amortized posteriorconditions = {"x": np.array([[0.0, 0.0]]).astype("float32")}# Prepare figuref, axes = plt.subplots(1, 4, figsize=(15, 6))# Obtain samples from the approximators (can also use the workflows' methods)nets = [flow_matching_workflow.approximator, consistency_model_workflow.approximator,affine_flow_workflow.approximator,spline_flow_workflow.approximator]names = ["Flow Matching", "Consistency Model", "Affine Coupling Flow", "Spline Coupling Flow"]colors = ["#153c7a", "#7a1515", "#157a2d", "#7a6f15"]for ax, net, name, color in zip(axes, nets, names, colors):# Obtain samplessamples = net.sample(conditions=conditions, num_samples=num_samples)["theta"]# Plot samplesax.scatter(samples[0, :, 0], samples[0, :, 1], color=color, alpha=0.75, s=0.5)sns.despine(ax=ax)ax.set_title(f"{name}", fontsize=16)ax.grid(alpha=0.3)ax.set_aspect("equal", adjustable="box")ax.set_xlim([-0.5, 0.5])ax.set_ylim([-0.5, 0.5])ax.set_xlabel(r"$\theta_1$", fontsize=15)ax.set_ylabel(r"$\theta_2$", fontsize=15)f.tight_layout()

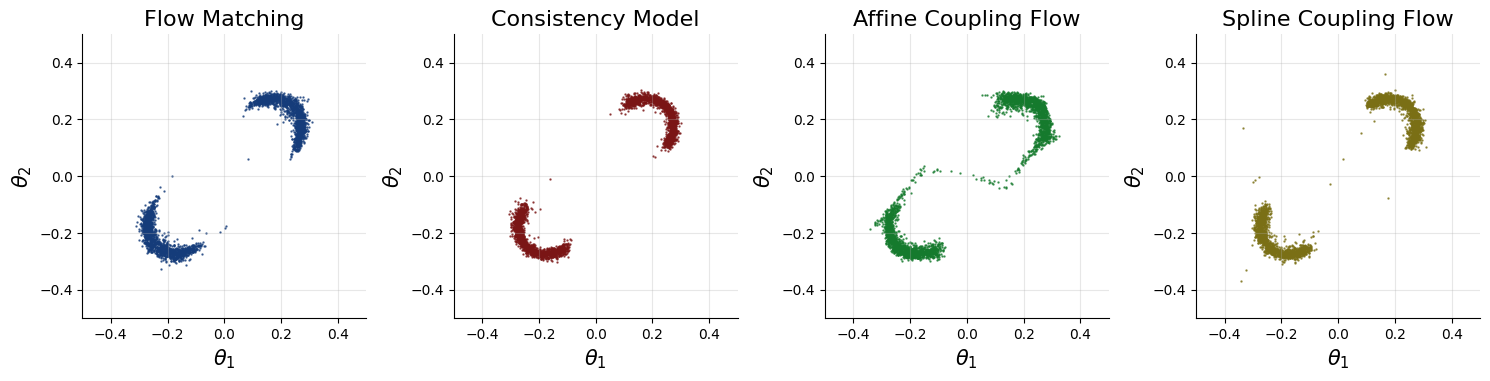
后验看起来如预期。但通常我们并不知道任何具体数据集的后验应长什么样。因此我们需要诊断方法来验证推断后验的正确性。一个这样的诊断是模拟基准校准（simulation-based calibration, SBC），由于摊销性的存在我们可以免费应用它。有关 SBC 和诊断图的更多细节，参见：

1. Talts, S., Betancourt, M., Simpson, D., Vehtari, A., & Gelman, A. (2018). Validating Bayesian inference algorithms with simulation-based calibration. arXiv preprint.
2. Säilynoja, T., Bürkner, P. C., & Vehtari, A. (2022). Graphical test for discrete uniformity and its applications in goodness-of-fit evaluation and multiple sample comparison. Statistics and Computing.
3. Martin Modrák 的实用 SBC 解释指南: https://hyunjimoon.github.io/SBC/articles/rank_visualizations.html