【CUDA进阶】MMA分析Bank Conflict与Swizzle（下）

前言

学习 UP 主 比飞鸟贵重的多_HKL 的 【CUDA进阶】MMA分析Bank Conflict与Swizzle（已完结） 视频，记录下个人学习笔记，仅供自己参考😄

refer 1：【CUDA进阶】MMA分析Bank Conflict与Swizzle（已完结）

refer 2：https://github.com/xlite-dev/LeetCUDA

refer 3：https://github.com/Bruce-Lee-LY/cuda_hgemm

refer 4：https://github.com/Chtholly-Boss/swizzle

refer 5：https://chatgpt.com

1. bank conflict 分析

在上篇文章 【CUDA进阶】MMA分析Bank Conflict与Swizzle（上） 中我们着重分析了 MMA 指令，主要是帮助大家理解在 MMA 指令执行以及 ldmatrix 中矩阵片段的布局规则，只有搞清楚了内存如何排布、数据如何传输之后我们才能去分析其中的 bank conflict 问题，不过在分析 bank conflict 之前，我们还是先回顾下 bank conflict 是什么

关于 bank conflict 我们在韩君老师的课程中有讲过，这里再简单过下，大家感兴趣的可以看看：二. CUDA编程入门-共享内存以及Bank Conflict

我们知道在 CUDA 编程中 32 个 thread 组成一个 warp，一般程序在执行的时候是以 warp 为单位去执行的，也就是说每 32 个 thread 一起执行同一指令，比如同时读/写数据。而 NVIDIA 硬件设计者为了让我们能够更高效的访问 shared memory 把它也分成了 32 个不同的部分，我们称之为 bank，分别对应 warp 中的 32 个线程，之后让每一个线程去访问它们其中的一个部分，如下图所示：

Note：一个 bank 字节宽度是 4 字节（32-bit，即 1 个 float，2 个 half）

我们假设一个 block 中包含 256 个线程，这 256 个线程访问 shared memory 的 32 个 bank 时的示意图如下所示：

一个理想的情况就是 warp 中的 32 个 thread 分别访问了 shared memory 中的 32 个不同的 bank，没有 bank conflict，而 bank conflict 指的就是在同一个 warp 内，有 2 个或者以上的线程访问了同一个 bank 上不同地址的内存，例如假设线程 0 访问到了 bank1 上线程 33 位置的内存，那么此时线程 0 和线程 1 就发生了 bank conflict

为了让大家更好的理解 bank conflict 是如何产生的，这里 UP 主准备了一些简单的示例代码来分析，这里 UP 主提供的一个例子是计算 16x16 * 16x16 的半精度矩阵乘法，即实现：

$$C_{16\times 16}=A_{16\times 16}+B_{16\times 16}$$

Note：为了更加直观的帮助我们分析，这里用小一点的矩阵维度，此外 kernel 启动的 block 数量是 1，每个 block 中 launch 的线程数是 32，恰好是一个 warp

首先我们来分析 V1 版本（v1_simple_wmma.cu）的代码，内容如下：

#include <iostream>
#include <cuda_runtime.h>
#include "common/tester.h"
#include "common/common.h"using namespace nvcuda;__global__ void wmma_simple_kernel(half* A, half* B, half* C){wmma::fragment<wmma::matrix_a, 16, 16, 16, half, wmma::row_major> a_frag;wmma::fragment<wmma::matrix_b, 16, 16, 16, half, wmma::row_major> b_frag;wmma::fragment<wmma::accumulator, 16, 16, 16, half> c_frag;wmma::load_matrix_sync(a_frag, A, 16);wmma::load_matrix_sync(b_frag, B, 16);wmma::fill_fragment(c_frag, 0.0f);wmma::mma_sync(c_frag, a_frag, b_frag, c_frag);wmma::store_matrix_sync(C, c_frag, 16, wmma::mem_row_major);
}void wmma_simple(half* A, half* B, half* C, int M, int N, int K){dim3 block(32);dim3 grid(1);wmma_simple_kernel<<<grid, block>>>(A, B, C);
}int main(int argc, char* argv[]){Tester tester(16, 16, 16, 1, 10, 100, true);tester.evaluate(wmma_simple, "wmma_simple");return 0;
}

V1 版本的实现非常简单，通过 WMMA 指令让该 warp 直接完成 16x16x16 的计算。在 V1 版本中不存在 bank conflict 问题，因为我们将数据从 global memory 直接搬运到了寄存器里面，中间没有经过 shared memory，但我们都知道半精度矩阵乘法很多的优化策略肯定是要涉及到 shared memory 的

因此我们接着来看第二个版本的实现（v2_shared_memory_wmma.cu）：

#include <iostream>
#include <cuda_runtime.h>
#include "common/tester.h"
#include "common/common.h"#define LDST128BITS(value) (reinterpret_cast<float4 *>(&(value))[0])using namespace nvcuda;__global__ void shared_memory_wmma_kernel(half* A, half* B, half* C){__shared__ half smem_a[16 * 16];__shared__ half smem_b[16 * 16];__shared__ half smem_c[16 * 16];int tx = threadIdx.x;LDST128BITS(smem_a[tx * 8]) = LDST128BITS(A[tx * 8]);LDST128BITS(smem_b[tx * 8]) = LDST128BITS(B[tx * 8]);__syncthreads();wmma::fragment<wmma::matrix_a, 16, 16, 16, half, wmma::row_major> a_frag;wmma::fragment<wmma::matrix_b, 16, 16, 16, half, wmma::row_major> b_frag;wmma::fragment<wmma::accumulator, 16, 16, 16, half> c_frag;wmma::load_matrix_sync(a_frag, smem_a, 16);wmma::load_matrix_sync(b_frag, smem_b, 16);wmma::fill_fragment(c_frag, 0.0f);wmma::mma_sync(c_frag, a_frag, b_frag, c_frag);wmma::store_matrix_sync(smem_c, c_frag, 16, wmma::mem_row_major);// sync threads not necessary when only 1 warp, but we will generalize it in// the future, so just keep it here__syncthreads();LDST128BITS(C[tx * 8]) = LDST128BITS(smem_c[tx * 8]);
}void shared_memory_wmma(half* A, half* B, half* C, int M, int N, int K){dim3 block(32);dim3 grid(1);shared_memory_wmma_kernel<<<grid, block>>>(A, B, C);
}int main(int argc, char* argv[]){Tester tester(16, 16, 16, 1, 10, 100, true);tester.evaluate(shared_memory_wmma, "shared_memory_wmma");return 0;
}

第二个版本相比于第一个版本唯一的区别就是这里做了一个看起来没有什么特别意义的一个操作，那就是先把数据从 global memory 搬运到 shared memory（每个线程要搬 8 个 half 数据），再由 shared memory 搬到寄存器里面

大家如果用 nsight compute 分析这个程序的话会发现它产生了 bank conflict：

Note：关于 nsight compute 的简单使用博主在 【CUDA调优指南】合并访存 文章中有提到过，这边就不再赘述了

我们可以点击 Location 查看 bank conflict 发生时对应的源码位置：

从图中可以清晰的看到 ncu 提示我们 load_matrix_sync 这个函数中发生了 bank conflict，对应的 SASS 指令是 LDSM.16.M88.4，下面我们来一起分析下为什么这个函数会发生 bank conflict，它的内部到底发生了些什么呢🤔

这就需要我们搞清楚 wmma::load_matrix_sync 内部具体是如何加载 16x16 的矩阵到 fragment 中的，上篇文章我们花费了大量的篇幅来跟大家讲 mma 指令 ldmatrix 以及矩阵加载布局图，那大家当时可能会困惑这和我们要讲的 bank conflict 有什么关系呢

那实际上 load_matrix_sync 指令底层的实现就是 mma 的 ldmatrix 指令，因此，如果我们想要搞清楚为什么 load_matrix_sync 会发生 bank conflict，实际上就是要搞清楚为什么 ldmatrix 会发生 bank conflict

我们先来看看 wmma::load_matrix_sync 内部发生了什么，wmma::load_matrix_sync 是 C++ WMMA API 的 fragment 加载接口，它用于从 shared memory 把一个或多个 8x8 half 子块 搬到寄存器的 fragment 布局里。它会被编译器降低到具体的 PTX/SASS 指令序列，在 Turing(SM75) 及之后，它通常会被降低为若干条 ldmatrix 指令（有时带 .trans、有时是 .x2/.x4）

上篇文章我们讲过 ldmatrix 的 基本搬运粒度 是 8x8（.m8n8），需要 8 个 线程提供 8 个起始行地址，若要一次性并行加载多个 8x8 子块可以通过 .num 指定（.x1/.x2/.x4），对于这里的 16x16 矩阵由 四个 8x8 小块拼成，编译器常用 ldmtrix.sync.aligned.m8n8.x4.shared.b16 指令把 16x16 需要的子块都装进 fragment

因此，在这里我们可以把 load_matrix_sync 指令简单理解为 PTX 指令 ldmatrx.x4 的封装（GPU 架构不同、布局不同，指令条数和变体可能不同，但逻辑如此）

那以上都只是我们的猜测，具体是不是这样的呢，load_matrix_sync 底层到底是不是 ldmatrix 指令呢，我们可以来简单验证下

首先，如果我们点击 wmma::load_matrix_sync 会发现它会跳转到 mma.hpp 头文件中，实现如下：

// 
// Load functions for frags of shape m16n16k16
// 
__CUDA_MMA_DEVICE_DECL__ void load_matrix_sync(fragment<matrix_a, 16, 16, 16, __half, row_major>& a, const __half* p, unsigned ldm) {
__hmma_m16n16k16_ld_a((int*)&a, (const int*)p, ldm, 0);
}

而我们再想看 __hmma_m16n16k16_ld_a 内部具体的实现就看不到了，因为它属于 NVCC 提供的 编译器内建（builtin/intrinsic），在头文件里只给了一个声明，真正的实现不在可见的 .cu/.hpp 源码中，也没有放在某个 .so 库中

那我们可以通过如下指令利用 CUDA 源文件来生成 PTX 中间代码：

nvcc -arch=sm_80 -ptx your.cu -o your.ptx

这里博主以 V2 版本源码，RTX4060Ti 显卡来做转换，指令如下：

nvcc -arch=sm_89 -ptx v2_shared_memory_wmma.cu -o v2_shared_memory_wmma.ptx

执行完成后在当前目录会生成 v2_shared_memory_wmma.ptx 文件，内容如下：

//
// Generated by NVIDIA NVVM Compiler
//
// Compiler Build ID: CL-31833905
// Cuda compilation tools, release 11.8, V11.8.89
// Based on NVVM 7.0.1
//.version 7.8
.target sm_89
.address_size 64// .globl	_Z25shared_memory_wmma_kernelP6__halfS0_S0_
// _ZZ25shared_memory_wmma_kernelP6__halfS0_S0_E6smem_a has been demoted
// _ZZ25shared_memory_wmma_kernelP6__halfS0_S0_E6smem_b has been demoted
// _ZZ25shared_memory_wmma_kernelP6__halfS0_S0_E6smem_c has been demoted.visible .entry _Z25shared_memory_wmma_kernelP6__halfS0_S0_(.param .u64 _Z25shared_memory_wmma_kernelP6__halfS0_S0__param_0,.param .u64 _Z25shared_memory_wmma_kernelP6__halfS0_S0__param_1,.param .u64 _Z25shared_memory_wmma_kernelP6__halfS0_S0__param_2
)
{.reg .b16 	%rs<2>;.reg .f32 	%f<2>;.reg .b32 	%r<56>;.reg .b64 	%rd<14>;// demoted variable.shared .align 2 .b8 _ZZ25shared_memory_wmma_kernelP6__halfS0_S0_E6smem_a[512];// demoted variable.shared .align 2 .b8 _ZZ25shared_memory_wmma_kernelP6__halfS0_S0_E6smem_b[512];// demoted variable.shared .align 2 .b8 _ZZ25shared_memory_wmma_kernelP6__halfS0_S0_E6smem_c[512];ld.param.u64 	%rd1, [_Z25shared_memory_wmma_kernelP6__halfS0_S0__param_0];ld.param.u64 	%rd2, [_Z25shared_memory_wmma_kernelP6__halfS0_S0__param_1];ld.param.u64 	%rd3, [_Z25shared_memory_wmma_kernelP6__halfS0_S0__param_2];cvta.to.global.u64 	%rd4, %rd2;cvta.to.global.u64 	%rd5, %rd1;mov.u32 	%r1, %tid.x;shl.b32 	%r2, %r1, 3;shl.b32 	%r3, %r1, 4;mov.u32 	%r4, _ZZ25shared_memory_wmma_kernelP6__halfS0_S0_E6smem_a;add.s32 	%r5, %r4, %r3;mul.wide.s32 	%rd6, %r2, 2;add.s64 	%rd7, %rd5, %rd6;ld.global.v4.u32 	{%r6, %r7, %r8, %r9}, [%rd7];st.shared.v4.u32 	[%r5], {%r6, %r7, %r8, %r9};mov.u32 	%r14, _ZZ25shared_memory_wmma_kernelP6__halfS0_S0_E6smem_b;add.s32 	%r15, %r14, %r3;add.s64 	%rd8, %rd4, %rd6;ld.global.v4.u32 	{%r16, %r17, %r18, %r19}, [%rd8];st.shared.v4.u32 	[%r15], {%r16, %r17, %r18, %r19};bar.sync 	0;mov.u32 	%r24, 16;wmma.load.a.sync.aligned.row.m16n16k16.shared.f16 	{%r25, %r26, %r27, %r28, %r29, %r30, %r31, %r32}, [%r4], %r24;wmma.load.b.sync.aligned.row.m16n16k16.shared.f16 	{%r33, %r34, %r35, %r36, %r37, %r38, %r39, %r40}, [%r14], %r24;mov.f32 	%f1, 0f00000000;// begin inline asm{  cvt.rn.f16.f32 %rs1, %f1;}// end inline asmmov.b32 	%r41, {%rs1, %rs1};cvta.to.global.u64 	%rd11, %rd3;wmma.mma.sync.aligned.row.row.m16n16k16.f16.f16 {%r42, %r43, %r44, %r45}, {%r25, %r26, %r27, %r28, %r29, %r30, %r31, %r32}, {%r33, %r34, %r35, %r36, %r37, %r38, %r39, %r40}, {%r41, %r41, %r41, %r41};mov.u32 	%r46, _ZZ25shared_memory_wmma_kernelP6__halfS0_S0_E6smem_c;wmma.store.d.sync.aligned.row.m16n16k16.shared.f16 	[%r46], {%r42, %r43, %r44, %r45}, %r24;bar.sync 	0;add.s64 	%rd13, %rd11, %rd6;add.s32 	%r47, %r46, %r3;ld.shared.v4.u32 	{%r48, %r49, %r50, %r51}, [%r47];st.global.v4.u32 	[%rd13], {%r48, %r49, %r50, %r51};ret;}

我们可以看到如下加载指令：

wmma.load.a.sync.aligned.row.m16n16k16.shared.f16 	{%r25, %r26, %r27, %r28, %r29, %r30, %r31, %r32}, [%r4], %r24;
wmma.load.b.sync.aligned.row.m16n16k16.shared.f16 	{%r33, %r34, %r35, %r36, %r37, %r38, %r39, %r40}, [%r14], %r24;

在 PTX 层我们看到的是 wmma 加载指令 wmma.load.a/b.sync.aligned.row.m16n16k16.shared.f16 并不是我们上面分析的 ldmatrix，但其实在 SASS（硬件指令层），ptxas 通常会把这些 wmma.load.* 降低成 LDSM 指令族（也就是我们常说的 ldmatrix 的 SASS 形态），整个转换过程其实是 C++ wmma::load_matrix_sync → PTX wmma.load.* → SASS LDSM（= ldmatrix）

我们可以进一步通过如下命名来确认：

nvcc -arch=sm_89 -cubin v2_shared_memory_wmma.cu -o v2_shared_memory_wmma.cubin
nvdisasm v2_shared_memory_wmma.cubin | grep -A2 -n LDSM

执行后终端输入如下：

上面的输出已经直接证明了 wmma::load_matrix_sync 在 SASS 层被编译成了 LDSM 指令（也就是硬件层面的 ldmatrix），其中：

• LDSM.16.M88.4 R12, [R21] ;
  • LSDM：ldmatrix 的 SASS 形式（Shared → Reg）
  • .16：每元素 16-bit（b16 / half）
  • M88：块大小 m8n8（一次处理 8x8）
  • .4：x4 一次性并行加载 4 个 8x8 子块（覆盖 16x16 的片段）
  • 这行对应 wmma.load.a.sync.aligned.m16n16k16.shared.f16 ...（A fragment，row_major，非转置）
• LDSM.16.MT88.4 R16, [R21+0x200] ;
  • MT88：带 T = transpose 的 m8n8（把行当列取）
  • 同样 .4 表示 x4
  • 这行对应 wmma.load.b.sync...，在 mma.sync.row.col 模式下常见的 “对 B 做转置加载”（内存里是 row_major，但 MMA 需要 col-major）
• 后面的 HMMA.16816.F16 ... 就是 Tensor Core 的 mma 计算（m16n8k16 形状，FP16），可以看到它被调用了两次，一次是 B 的前 8 列，另一次是 B 的后 8 列，两条 HMMA.16816 来完成 m16n16k16

因此，经过上面的分析我们知道 wmma 一些函数在硬件层面上会被拆分成更加底层的 mma 指令，这也是我们上篇文章花费大量篇幅讲解 mma 指令的原因，分析 WMMA 接口 load_matrix_sync 产生的 bank conflict 问题实际上就是来分析 mma 中 ldmatrix 指令的 bank conflict 问题，也就需要我们对 ldmatrix 执行过程中内存排布、数据加载有所了解

那我们就一起来看看这个过程是如何产生 bank conflict 的，现在我们可以认为分析的是 ldmatrix.sync.aligned.x4.m8n8.shared.b16 这条 mma 指令，对应的矩阵 fragment 的布局图如下：

上图可以分为 4 个 8x8 组别，每个组别各需要 8 个线程提供 8 个 shared memory 的起始行地址，总共需要 32 个线程即一个 warp 来提供 32 个地址。另外需要注意的是每个组别负责的 8x8 矩阵中所有的元素并不是只加载到提供行起始地址的 8 个线程的寄存器中，而是加载到 warp 内 32 个线程的各个寄存器中

博主绘制了一个草图来说明 16x16 大小的矩阵中 shared memory 中各个 bank 的分布图和 fragment 布局图的对应关系：

从图中我们可以看到，以 bank0 为例，线程 0 和线程 16 同时访问读取了 bank0 中的不同地址，有 2 路 bank conflict 存在

那大家可能有些困惑，这里只发生了 2 路 bank conflict，加上 B 矩阵的 2 路，一共是 4 才对，为什么 ncu 的表格 Shared Load Matrix 一栏中 Bank Conflicts 显示的是 8 呢？这边博主查了一些资料和大家一起讨论下，不一定对

首先，一条 LDSM.16.M88.4（也就是 ldmatrix.x4）：

• 表示 warp 32 线程要取一个 16x16 的 tile
• 内部拆分成 4 个 8x8 子块
• 每个子块（8x8）的并行取数操作可以理解为一个 wavefront
• 每个 wavefront 8 线程，每线程提供一行基址

而 ncu 表格中的统计方式是针对于 wavefront 而言的，对于每个 wavefront，nsight compute 都会问：“在这 8 个线程发出的请求里，是否有 2 个以上线程落在同一个 bank 的不同地址？”

• 是 → 这个 wavefront 记 1 次 bank conflict
• 不是 → 这个 wavefront 记 0 次 bank conflict
• ⚠️注意：在统计时不会在一个 wavefront 里按冲突路数叠算（例如哪怕有 4 路 bank conflict，也只算 1）

只要保证每个 wavefront（即每个组别）内部线程的访问没有冲突，那么这条 ldmatrix 整体就不会产生 bank conflict

因此，A 矩阵的 ldmatrix 的四个组别都产生了 bank conflict 所以记 4，同理 B 也有 4，所以我们在 ncu 分析表格中看到的就是 8。

还有一个点需要探讨下，那就是在 v2_shared_memory_wmma.cu 的代码中数据从 global memory 加载到 shared memory 过程中到底有没有发生 bank conflict 呢？

首先，博主按照自己的理解绘制了一个示意图，如下所示：

在上图中，以 bank0 为例，我们可以清晰的看到 T0、T8、T16、T24 分别访问了 bank0 的不同地址，有 4 路 bank conflict 存在。因此，博主最开始认为数据在 global memory 到 shared memory 传输的过程中是产生了 bank conflict 的，但是从 ncu 的分析结果来看这个过程似乎并没有产生 bank conflict，那为什么会这样呢？🤔

在 UP 主的视频中也花了一些时间来讲解这个问题，他认为这个过程没有发生 bank conflict 的原因是：当一个线程访问的数据超过 4 个字节时，它会被拆分成多个内存事务，而每个内存事务最多能访问 128B，相当于是 8 个线程，所以只要你保证这 8 个线程不产生 bank conflict，那整体就没有冲突

UP 提到的关于内存事务的说法我们在 【CUDA调优指南】合并访存 文章中有提到过，当时提到的内存事务还是和 global memory 的访存合并相关，博主认为它和 shared memory 中的 bank conflict 并没有什么关系，以下是博主在查找资料时认为比较正确的说法，但不一定对

UP 的观点感觉上有以下几点被误解：

误解 1：关于 cache line（缓存行）和 128 字节

• global memory 的缓存行确实是 128 字节，但这 仅使用于 global memory 访问，不适用于 shared memory 的 bank conflict 分析
• shared memory 的 bank 机制是独立的，与 global memory 的缓存行无关

误解 2：关于每个内存事务最多能访问 128B，相当于是 8 个线程

• 这是对 global memory 访存合并规则的描述，不适用于 shared memory 的 bank conflict 分析
• shared memory 的 bank conflict 只关心 哪些 bank 被同时访问，不涉及内存事务大小的限制

误解 3：关于保证这 8 个线程不产生 bank conflict

• shared memory 的 bank conflict 是在 整个 warp（32 线程）层面 分析的
• 即使前 8 个线程没有冲突，但如果后续线程重复访问相同的 bank，仍然会产生冲突

但是从 ncu 分析的结果来看，数据在从 global memory 到 shared memory 确实是没有 bank conflict 的，那是什么原因呢，博主又找了一些资料，然后也问了几个 AI，有的说存在冲突有的说不存在冲突，其中有个说不存在 bank conflict 的回答，博主认为有些许道理，因此贴在下面：(from doubao)

shared memory 的读写操作在硬件层面上存在一些差异，导致 bank conflict 在读写操作判定时也存在一些差异，具体表现如下：

操作类型	同一 bank 的不同地址	同一 bank 的相同地址
写入	无冲突（并行支持）	冲突（结果不确定）
读取	冲突（序列化）	无冲突（广播机制）

为什么写入同一 bank 的不同地址不冲突呢？这主要是因为 shared memory 的写入路径设计了 多端口并行写入电路，允许：

• 多个线程在 同一时钟周期 内，向 同一个 bank 的不同地址 写入数据（例如上图中线程 0 和线程 8 访问 bank0 的不同地址属于这种情况）
• 只要不是写入 完全相同的地址（即内存地址不重叠），硬件就能并行处理这些写入请求

这是因为写入操作的目的是“修改内存内容”，只要地址不重叠，硬件可以通过内部电路同时完成多个写入（类似“多个人同时往不同抽屉里放东西，互不干扰”）

为什么读取同一 bank 的不同地址会冲突呢？这主要是因为与写入不同，shared memory 的 读取路径每个 bank 只有一个读取端口：

• 多个线程在同一时钟周期读取 同一 bank 的不同地址 时，硬件无法并行处理，必须按顺序（序列化）执行（类似“多个人同时想从同一个抽屉取不同东西，只能排队一个个来”）
• 这种序列化会导致访问延迟增加（即 bank conflict）

因此，写入阶段（即 global memory → shared memory）是没有 bank 冲突的，而读取阶段（即 shared memory → register）则存在 bank 冲突

那这里我们的重点还是放在 ldmatrix 也就是数据从 shared memory → register 阶段的 bank conflict 问题的分析与解决上

2. 通过 padding 解决 bank conflict

OK，上个小节我们分析了 WMMA 接口 load_matrix_sync 中 bank conflict 问题产生的原因，那要怎么来解决它呢

这个小节我们来看解决 bank conflict 的第一种方式，padding。怎么通过 padding 的方式来解决 bank 冲突呢，很简单，只需要在我们申请 shared memory 的时候多申请一块就行，代码如下（v3_shared_memory_wmma_padding.cu）：

#include <iostream>
#include <cuda_runtime.h>
#include "common/tester.h"
#include "common/common.h"#define LDST128BITS(value) (reinterpret_cast<float4 *>(&(value))[0])using namespace nvcuda;__global__ void shared_memory_wmma_padding_kernel(half* A, half* B, half* C){__shared__ half smem_a[16][16 + 8];__shared__ half smem_b[16][16 + 8];__shared__ half smem_c[16 * 16];int tx = threadIdx.x;LDST128BITS(smem_a[tx / 2][(tx % 2) * 8]) = LDST128BITS(A[tx * 8]);LDST128BITS(smem_b[tx / 2][(tx % 2) * 8]) = LDST128BITS(B[tx * 8]);__syncthreads();wmma::fragment<wmma::matrix_a, 16, 16, 16, half, wmma::row_major> a_frag;wmma::fragment<wmma::matrix_b, 16, 16, 16, half, wmma::row_major> b_frag;wmma::fragment<wmma::accumulator, 16, 16, 16, half> c_frag;wmma::load_matrix_sync(a_frag, smem_a[0], 16 + 8);wmma::load_matrix_sync(b_frag, smem_b[0], 16 + 8);wmma::fill_fragment(c_frag, 0.0f);wmma::mma_sync(c_frag, a_frag, b_frag, c_frag);wmma::store_matrix_sync(smem_c, c_frag, 16, wmma::mem_row_major);// sync threads not necessary when only 1 warp, but we will generalize it in// the future, so just keep it here__syncthreads();LDST128BITS(C[tx * 8]) = LDST128BITS(smem_c[tx * 8]);
}void shared_memory_wmma_padding(half* A, half* B, half* C, int M, int N, int K){dim3 block(32);dim3 grid(1);shared_memory_wmma_padding_kernel<<<grid, block>>>(A, B, C);
}int main(int argc, char* argv[]){Tester tester(16, 16, 16, 1, 10, 100, true);tester.evaluate(shared_memory_wmma_padding, "shared_memory_wmma_padding");return 0;
}

在 V2 版本中我们为 A、B 矩阵申请的 shared memory 大小为 16x16，这里我们多申请一部分，每一行多申请 8 列的大小，也就是 16x(16+8)，相当于做了一个 padding

那我们来看下加入 padding 后的 bank 分布图和 fragment 布局图会发生什么变化呢：

可以看到由于我们 padding 了 8 列（16-23）导致 shared memory 中 bank 分布图发生了变化，由于 padding 的存在，线程 T0 和 T16 现在访问了不同的 bank，线程 T0 访问的是 bank0，线程 T16 访问的是 bank16

如果大家细心的话会发现虽然 T0 和 T16 访问了不同的 bank，但从图上看此时 T0 和 T20 同时访问了 bank0，不同线程访问了同一 bank，应该也是会有 bank conflict 的，那为什么说 padding 能解决 bank conflict 呢？🤔

那这点我们在前面其实已经解释过了，我们知道 ldmatrix 的 基本粒度是 8x8，也就是用 8 个线程加载一个 8x8 tile，要加载 16x16 的 tile 需要将 warp 内的 32 个线程拆分成 4 组，每组 8 线程，每组负责加载一个 8x8 tile。虽然上图中我们将这四个子组负责的数据区域绘制在了一起，但这并不代表着四个子组是同时加载 8x8 子块的，而是 被分组执行的

换句话说，虽然编译器把四个 8x8 的加载合并为一条 .x4 形式，但在 SM 内部仍然以 8 线程为一组 去取各自 8x8 数据，也正因如此，是否有 shared bank conflict，要看“每组 8 线程”的访问分布，不同组即使命中同一个 bank，也不构成 bank conflict

上图中虽然线程 T0 和 T20 都访问了 bank0，但它并没有真正产生 bank conflict，因为它们属于不同的 8 线程子组，所以 padding 方法确实解决了 bank conflict 问题

我们通过 ncu 可以看到 ldmatrix 部分的 bank conflict 确实有所缓解：

这里 ncu 分析的 Shared Store 结果为 12，其中有一部分是由于 smem_c 没有 padding 导致的，还有一部分博主通过 Location 发现是 global memory 到 shared memory 加载导致的，如下图所示：

这是怎么回事呢？其中 padding 之后的访问图如下所示：

前面博主分析的是 shared memory 在写入时存在多个端口，只要不在同一个 bank 的相同地址写就行，但是这里显然不符合，博主暂时也没搞清楚，也可能是前面分析的有问题，但是总之 ldmatrix 产生的 bank conflict 是通过 padding 方式解决了的

虽然 padding 这种方法可以有效缓解 bank conflict，但它占用了更多共享内存，带宽利用率也下降了，那有没有更好的解决方法呢？有的，这就是我们下面要学习的 swizzle（地址重排）方法

3. mma 搭配 wmma 实现矩阵乘法计算

swizzle 方法通过 逻辑地址重排 解决 bank conflict 问题，它不像 padding 那样增加物理内存，而是通过 确定性的数学函数（如异或、模运算、位重排等）打乱线程与数据列的映射关系，使原本集中在不同 bank 的访问分散到不同 bank。

其核心是打破访问地址的 bank 索引周期—例如，当线程按固定步长访问时，通过地址变换让新的访问步长与 bank 数量互质，从而避免同一时钟周期内多个线程访问同一 bank。这种方法无额外内存开销，但效果依赖于映射函数与实际访问模式的匹配度，可能引入少量地址计算开销。

在我们正式讲解 swizzle 方法之前，需要先用 mma 指令来实现之前的 16x16 的矩阵乘法计算，这主要因为 WMMA 被封装好了，导致它不能为每个 lane 指定各自地址，也不能控制 ldmatrix 与 lane 子组的映射。WMMA 只能配合 padding 这种 不改变几何地址关系 的做法，它不支持 改变地址到 bank 的映射函数（swizzle）

因此如果我们想用 swizzle（地址重排）来规避 shared memory → register 的 bank conflict，就得下沉到 MMA/PTX 级，不是因为 MMA 性能更高，而是 WMMA 把很多关键细节都封死了，我们没法插手做想要的地址重排与寄存器布局

3.1 代码实现

所以我们首先要做的就是将 V2 版本的 WMMA 的代码转换成 V4 版本的 MMA 代码（v4_shared_memory_mma.cu），内容如下所示：

#include <iostream>
#include <cuda_runtime.h>
#include "common/tester.h"
#include "common/common.h"#define REG(val) (*reinterpret_cast<uint32_t*>(&(val)))
#define HALF2(val) (*reinterpret_cast<half2*>(&val))
#define LDST128BITS(value) (reinterpret_cast<float4 *>(&(value))[0])using namespace nvcuda;__device__ __forceinline__ void ldmatrix_sync(half* dst, void* addr){asm volatile("ldmatrix.sync.aligned.x4.m8n8.shared.b16 {%0, %1, %2, %3}, [%4];": "=r"(REG(dst[0])), "=r"(REG(dst[2])), "=r"(REG(dst[4])), "=r"(REG(dst[6])): "l"(__cvta_generic_to_shared(addr)));
}__device__ __forceinline__ void ldmatrix_trans_sync(half* dst, void* addr){asm volatile("ldmatrix.sync.aligned.x4.m8n8.shared.trans.b16 {%0, %1, %2, %3}, [%4];": "=r"(REG(dst[0])), "=r"(REG(dst[2])), "=r"(REG(dst[4])), "=r"(REG(dst[6])): "l"(__cvta_generic_to_shared(addr)));
}__device__ __forceinline__ void mma_sync_m16n8k16(half* c, half* a, half* b){asm volatile("mma.sync.aligned.m16n8k16.row.col.f16.f16.f16.f16 {%0, %1}, {%2, %3, %4, %5}, {%6, %7}, {%8, %9};": "=r"(REG(c[0])), "=r"(REG(c[2])): "r"(REG(a[0])), "r"(REG(a[2])), "r"(REG(a[4])), "r"(REG(a[6])), "r"(REG(b[0])), "r"(REG(b[2])), "r"(0), "r"(0));
}__device__ __forceinline__ void stmatrix_sync(half* dst, half* src){// ! Ampere doesn't have stmatrix.sync, we should simulate ituint64_t private_addr = (uint64_t)dst;uint64_t shared_addr[4];
#pragma unrollfor(int i = 0; i < 4; ++i){shared_addr[i] = __shfl_sync(0xFFFFFFFF, private_addr, i * 8 + threadIdx.x / 4);}
#pragma unrollfor(int i = 0; i < 4; ++i){*(reinterpret_cast<half2*>(shared_addr[i]) + threadIdx.x % 4) = HALF2(src[2 * i]);}
}__global__ void shared_memory_mma_kernel(half* A, half* B, half* C){__shared__ half smem_a[16 * 16];__shared__ half smem_b[16 * 16];__shared__ half smem_c[16 * 16];int tx = threadIdx.x;LDST128BITS(smem_a[tx * 8]) = LDST128BITS(A[tx * 8]);LDST128BITS(smem_b[tx * 8]) = LDST128BITS(B[tx * 8]);__syncthreads();wmma::fragment<wmma::matrix_a, 16, 16, 16, half, wmma::row_major> a_frag;wmma::fragment<wmma::matrix_b, 16, 16, 16, half, wmma::row_major> b_frag;wmma::fragment<wmma::accumulator, 16, 16, 16, half> c_frag;wmma::fill_fragment(c_frag, 0.0f);uint32_t row = tx % 16;uint32_t col = tx / 16;ldmatrix_sync(a_frag.x, smem_a + row * 16 + col * 8);ldmatrix_trans_sync(b_frag.x, smem_b + row * 16 + col * 8);// 2 m16n8k16 HMMA to achieve m16n16k16 matrix multiplicationmma_sync_m16n8k16(c_frag.x, a_frag.x, b_frag.x);mma_sync_m16n8k16(c_frag.x + 4, a_frag.x, b_frag.x + 4);// wmma::store_matrix_sync(smem_c, c_frag, 16, wmma::mem_row_major);stmatrix_sync(smem_c + row * 16 + col * 8, c_frag.x);__syncthreads();LDST128BITS(C[tx * 8]) = LDST128BITS(smem_c[tx * 8]);
}void shared_memory_mma(half* A, half* B, half* C, int M, int N, int K){dim3 block(32);dim3 grid(1);shared_memory_mma_kernel<<<grid, block>>>(A, B, C);
}int main(int argc, char* argv[]){Tester tester(16, 16, 16, 1, 10, 100, true);tester.evaluate(shared_memory_mma, "shared_memory_mma");return 0;
}

上面的 V4（MMA/PTX）版本正是把 “WMMA 黑盒” 拆开来手动实现，下面我们来分析下它是如何完成一次 m16n16k16 半精度矩阵乘法计算的：(from ChatGPT)

1. 线程/子块划分

• block 启动 1 个 warp（32 线程）计算一个 16x16 C-tile
• 共享内存：smem_a/b/c 各存一块 16x16
• 线程内坐标：

uint32_t row = tx % 16;   // 0..15
uint32_t col = tx / 16;   // 0/1  (表示左/右 8 列半块)

2. gmem → smem 的装填

LDST128BITS(smem_a[tx * 8]) = LDST128BITS(A[tx * 8]);
LDST128BITS(smem_b[tx * 8]) = LDST128BITS(B[tx * 8]);

• 每个线程向量化加载 8 个 half，16 字节数据，和 V2 版本保持一致

3. 从 smem 取片段（ldmatrix 指令）

ldmatrix_sync(a_frag.x, smem_a + row * 16 + col * 8);
ldmatrix_trans_sync(b_frag.x, smem_b + row * 16 + col * 8);

• 这两个函数对应的 mma 指令分别是：
  • ldmatrix.sync.aligned.x4.m8n8.shared.b16（A：不转置）
  • ldmatrix.sync.aligned.x4.m8n8.shared.trans.b16（B：转置）
• .m8n8.x4：一次覆盖 4 个 8x8 子块，warp 内 32 线程被内部划分为 4（8 线程） 子组,每组提供 8 行起始地址，各取一个 8x8
• .trans：转置，把共享内存中的行当列读取（常用于 mma.sync.row.col 下的 B）
• 地址 row * 16 + col * 8：
  • col = 0 取 0…7 列半块，col = 1 取 8…15 列半块
  • 4 组恰好覆盖 [0:8,0:8]、[8:16,0:8]、[0:8,8:16]、[8:16,8:16] 这四个子块
  • 输出约束里用 REG(dst[0]), REG(dst[2]) ...：本质是用 4 个 32-bit 物理寄存器接住 8x8x4 的 packed half 数据（每个寄存器装两个 half）

4. 在 Tensor Core 上做乘加（两条 HMMA 拼 16x16）

mma_sync_m16n8k16(c_frag.x,     a_frag.x, b_frag.x);
mma_sync_m16n8k16(c_frag.x + 4, a_frag.x, b_frag.x + 4);

• 指令：mma.sync.aligned.m16n8k16.row.col.f16.f16.f16.f16
• 形状 m16n8k16
  • 第一次用 B 的前半（n=0…7），产出 C 的左半块 m16n8
  • 第二次用 B 的后半（n=8…15），产出 C 的右半块 m16n8
  • 两条合起来就是 m16n16k16

5. 把 C 片段写回 smem（模拟 stmatrix）

stmatrix_sync(smem_c + row * 16 + col * 8, c_frag.x);

• Ampere 架构没有 stmatrix.sync，这里用 warp 内 shuffle 模拟实现
  • 每个 lane 先广播出 4 个目标地址（来自 lanes i * 8 + lane / 4），对应 4 个 8x8 子块
  • 然后每个 lane 把自己寄存器里那份 half2 写到相应地址偏移（threadIdx.x % 4）

6. smem → gmem 回写

LDST128BITS(C[tx * 8]) = LDST128BITS(smem_c[tx * 8]);

V4 版本代码用两条 mma.m16n8k16 完成 m16n16k16，ldmatrix(.trans).m8n8.x4 负责从共享读四个 8x8 子块，最后用自己实现的 stmatraix.sync 把 C 写回共享，相比于 V2 版本实现，这里把 WMMA “黑盒” 封装拆开，我们可以控制每个 lane 的地址，这正是实现 swizzle 的前提

3.2 补充：stmatrix_sync 函数分析

关于 stmatrix_sync 函数的实现博主有些困惑，这里稍微解释下：(from doubao)

stmatrix 是为了模拟 Ampere 架构中缺失的 stmatrix.sync 硬件指令 而实现的函数。其核心功能是将线程私有的矩阵数据（src）协作存储到共享内存（dst）中，确保线程间数据的正确同步和布局，以匹配矩阵片段加载（如 mma.ldmatrix）的内存访问模式。

函数通过两个关键步骤实现共享内存的同步存储，核心依赖线程束（warp）内的线程协作和 __shfl_sync 指令：

__device__ __forceinline__ void stmatrix_sync(half* dst, half* src){// 1. 收集所有线程的共享内存目标地址uint64_t private_addr = (uint64_t)dst;  // 当前线程的目标共享内存地址uint64_t shared_addr[4];                // 存储收集到的其他线程的目标地址
#pragma unrollfor(int i = 0; i < 4; ++i){// 通过__shfl_sync收集不同线程的目标地址shared_addr[i] = __shfl_sync(0xFFFFFFFF, private_addr, i * 8 + threadIdx.x / 4);}// 2. 线程协作将数据写入共享内存
#pragma unrollfor(int i = 0; i < 4; ++i){// 每个线程负责写入共享内存的特定位置*(reinterpret_cast<half2*>(shared_addr[i]) + threadIdx.x % 4) = HALF2(src[2 * i]);}
}

步骤 1：收集共享内存目标地址（shared_addr 填充）

• private_addr：当前线程要写入的共享内存起始地址（dst 的地址）。
• 循环通过 __shfl_sync 从其他线程收集目标地址，存储到 shared_addr 数组中：
  • i * 8 + threadIdx.x / 4：计算源线程索引（srcLane），由于线程块大小为32（block(32)），threadIdx.x 范围是 0~31，threadIdx.x / 4 得到 0~7（每 4 个线程一组），结合 i=0~3，最终覆盖线程束内所有 32 个线程（0~31）
  • 结果：shared_addr 数组收集了线程束内所有线程的共享内存目标地址，实现了线程间地址信息的同步交换

步骤 2：协作写入共享内存

• 每个线程通过 shared_addr[i] 获取其他线程的目标地址，结合自身索引（threadIdx.x % 4）定位到具体写入位置：
  • reinterpret_cast<half2*>(shared_addr[i])：将共享内存地址转换为 half2 指针（half2 是 2 个 half 的组合，16 位）
  • + threadIdx.x % 4：每个线程负责写入该地址起始的第 0~3 个 half2 元素（因为 threadIdx.x % 4 范围是 0~3）
  • 写入数据：HALF2(src[2 * i]) 将 src 中的 half 数据转换为 half2 类型写入，确保内存对齐和高效访问

其实就是下图所示的矩阵片段 C 的布局（16x8），只是要将其向右复制一份变为 16x16

同步机制

• 函数未使用 __syncthreads()（块级同步），而是依赖 线程束内的隐式同步：
  • 线程束（32线程）内的线程执行是“锁步”的（同一指令周期执行相同指令）
  • __shfl_sync 本身是线程束内的同步指令，确保所有参与的线程在交换数据后再继续执行，避免了数据访问冲突
  • 最终通过线程间的地址交换和分工写入，实现了共享内存存储的“同步”效果（数据按预期布局正确写入）

3.3 补充：__shfl_sync 函数详解

1. 函数原型

__shfl_sync 是 CUDA 提供的线程束内数据交换 intrinsic 函数，原型如下（以 32 位无符号整数为例）：

unsigned int __shfl_sync(unsigned int mask,    // 线程掩码：指定参与交换的线程unsigned int var,     // 要交换的变量int srcLane,          // 源线程索引（提供数据的线程在束内的位置，0~31）int width = 32        // 线程束内的子组大小（默认32，可选16、8等）
);

2. 核心功能

在 同一个线程束（warp） 内的线程间交换数据，无需通过共享内存或全局内存，直接通过寄存器传递，效率极高

• 线程束是 GPU 的基本执行单元（通常 32 个线程），同一束内的线程执行相同指令流
• __shfl_sync 允许束内任意线程从其他线程（srcLane 指定）获取数据，实现低延迟的数据共享

3. 参数解析

• mask：32 位掩码，每一位对应线程束内的一个线程（bit0 对应 lane0，bit1 对应 lane1，…）。只有掩码为 1 的线程参与交换，未参与的线程返回自身的 var。 例：0xFFFFFFFF 表示所有 32 个线程都参与
• var：当前线程要交换的数据（可以是整数、浮点等基本类型）
• srcLane：提供数据的源线程索引（0~width-1）。若 srcLane 超出范围，行为未定义
• width：线程束内的子组大小（默认32），用于将束划分为更小的子集（如16线程），srcLane 仅在子组内有效

4. 示例说明

假设有一个 32 线程的束，threadIdx.x 为0~31（对应束内索引 lane=0~31）：

int lane = threadIdx.x % 32;          // 束内线程索引
int data = lane * 10;                 // 每个线程的初始数据
int srcLane = (lane + 2) % 32;        // 源线程索引（当前线程+2）
int result = __shfl_sync(0xFFFFFFFF, data, srcLane);  // 交换数据

• 执行后，lane=0 的线程会得到 lane=2 的数据（20），lane=1 得到 lane=3 的数据（30），以此类推，实现线程间的数据环移

5. 在 stmatrix_sync 中的作用

__shfl_sync 在这里的核心作用是 收集线程束内所有线程的共享内存目标地址：

• 每个线程通过 __shfl_sync 从其他线程（i * 8 + threadIdx.x / 4 计算的 srcLane）获取它们的 private_addr（目标共享内存地址）
• 最终 shared_addr 数组包含了所有线程的目标地址，为后续线程协作写入共享内存提供了基础

4. swizzle 原理讲解

这个小节我们正式来讲解如何用 swizzle 解决 bank conflict

我们先来看下正常数据加载的流程，也就是没有使用 swizzle 的情况，如下图所示：

Figure 1: data loading from global memory to registers without swizzle

如上图所示，原始 16x16 矩阵数据存储在 global memory 中，通过一个 warp 即 32 个线程加载到 shared memory 中，每个 thread 负责加载 8 个 half。接着通过 mma 指令 ldmatrix.x4 将 shared memory 中的数据加载到各个线程的寄存器中，布局如上图所示

前面小节我们说过 ldmatrix 的基本粒度是 8x8 即 .m8n8，因此 16x16 大小的数据加载需要 4 个组别，每个组别 8 个线程，每个线程负责提供一个起始行地址，而在这个过程中有没有发生 bank conflict 取决于每个组别的 8 个线程在加载 shared memory 数据到寄存器中时有没有发生冲突，而不是取决于所有组别

以左上角 8x8 粒度的组别（记组别 1）为例，从图中我们能明显的看到线程 T16-T19 与线程 T0-T15 发生了 bank conflict，因为 T16 和 T0 都访问了 bank0、T17 和 T1 都访问了 bank1、…，也就是 addr4-addr7 这部分的线程访问的 bank 和 addr0-addr3 这部分线程访问的 bank 相同，因此产生了 bank conflict

那我们接着看使用了 swizzle 后的数据加载情况，如下图所示：

Figure 2: data loading from global memory to registers with swizzle

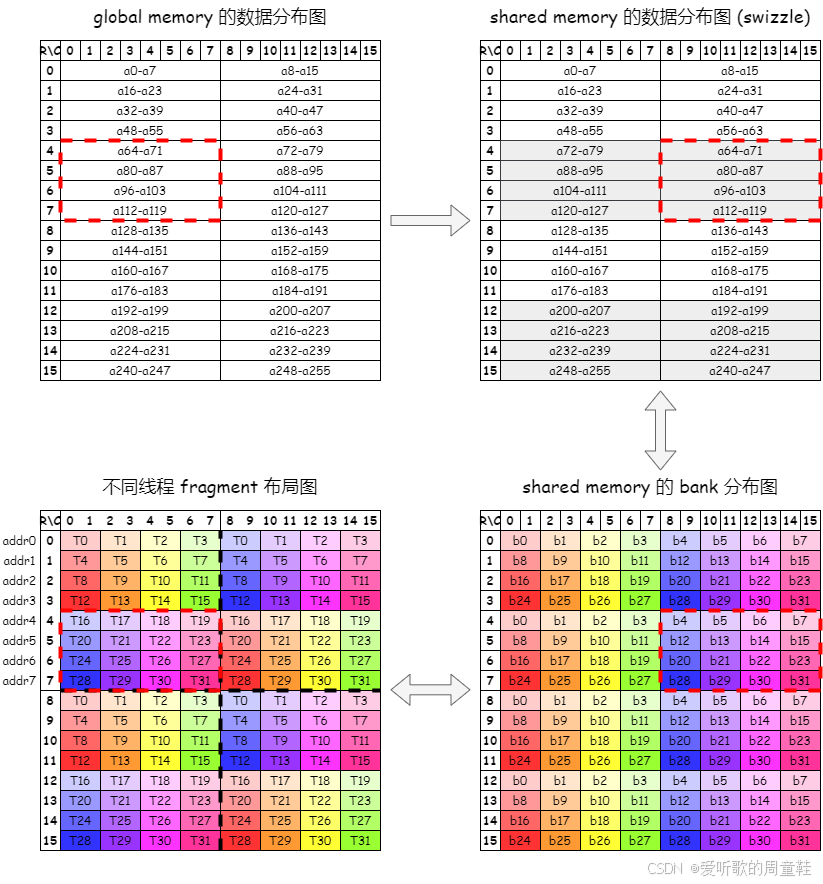
上面这个过程与前面有什么区别呢，首先数据从 global memory 加载到 shared memory 发生了变化，原本在 shared memory 中 smem[4…7, 0…7] 位置要加载 gmem[4…7, 0…7] 位置的数据，即 a64-a71、a80-a87、a96-a103、a112-119 这 32 个 half 数据，但此时发生了变化 smem[4…7, 0…7] 位置不再加载 gmem[4…7, 0…7] 位置的数据，取而代之的是加载 gmem[4…7, 8…15] 位置的数据，也就是加载的是 4-7 行后半列的数据，而 smem[4…7, 8…15] 位置加载的是 gmem[4…7, 0…7] 位置的数据，刚好反过来了。

同理 smem[12…15, 0…7] 位置加载的是 gmem[12…15, 8…15] 位置的数据，而 smem[12…15, 8…15] 位置加载的是 gmem[12…15, 0…7] 位置的数据，其它位置的数据加载不变

那除此之外还有什么变化呢，还有一个就是寄存器从 shared memory 加载数据的位置发生了变化，以组别 1 为例，以前 addr4-addr7 提供的起始行地址是 smem[4, 0]、smem[5, 0]、smem[6, 0]、smem[7, 0]。而现在不一样了，现在 addr-addr7 提供的起始行地址变成了 smem[4, 8]、smem[5, 8]、smem[6, 8]、smem[7, 8]

为什么起始行地址变成了这四个呢，这是因为 global memory 到 shared memory 的数据方式发生了变化，注意组别 1 的 addr4-addr7 这部分还是需要加载 a64-a71、a80-a87、a96-a103、a112-119 这 32 个 half 数据，那大家可能会困惑为什么还需要加载这 32 个 half 数据呢？

这是因为我们在寄存器 fragment 只有取到这部分的数据，其布局才能和原始矩阵即 global memory 中的布局保持一致，才能确保后续矩阵乘法不会出错，而此时大家会发现这 32 个 half 数据被存储到了 shared memory 的 smem[4, 8…15]、smem[5, 8…15]、smem[6, 8…15]、smem[7, 8…15] 位置

不知道大家这个能不能理解，就是我的布局方式是没变的，从 global memory 到寄存器 fragment 的数据布局是没有发生改变的，我要保持之前的布局去取我想要的数据那就要改变起始行地址的位置，这样才能从 shared memory 中拿到我想要的数据

所以大家要注意使用了 swizzle 时的 shared memory 的 bank 分布和寄存器 fragment 布局图没有任何改变，它只改变了 global memory 到 shared memory 之间数据的加载方式，也就是说各个寄存器去 shared memory 中取数据的位置发生了变化，仅此而已

这样做完之后我们会惊奇的发现原来的 bank conflict 问题不复存在了！为什么呢，我们来简单分析下就知道了，以组别 1 为例，之前组别 1 的 addr4-addr7 会与 addr0-addr3 冲突，是因为都访问了同一个 bank。但现在不同了，现在由于 addr4-addr7 依旧要去取 global memory 红色框 部分的数据，即 a64-a71、a80-a87、a96-a103、a112-119 这 32 个 half 数据

而这 32 个 half 数据被存储到了 smem[4, 8…15]、smem[5, 8…15]、smem[6, 8…15]、smem[7, 8…15] 位置，而这些位置对应的 bank 是 b4-b31，恰好是 addr0-addr3 中的线程所没有访问的 bank，完美解决了 bank conflict 问题

那通过上面分析后大家会发现 swizzle 这个方法其实非常的巧妙，我仅仅只改变了数据加载到 shared memory 的位置就能解决困扰我们的 bank conflict 问题，

OK，原理我们就分析到这里，下面我们来看代码是怎么实现的（v5_shared_memory_mma_swizzle.cu）：

#include <iostream>
#include <cuda_runtime.h>
#include "common/tester.h"
#include "common/common.h"#define REG(val) (*reinterpret_cast<uint32_t*>(&(val)))
#define HALF2(val) (*reinterpret_cast<half2*>(&val))
#define LDST128BITS(value) (reinterpret_cast<float4 *>(&(value))[0])using namespace nvcuda;__device__ __forceinline__ void ldmatrix_sync(half* dst, void* addr){asm volatile("ldmatrix.sync.aligned.x4.m8n8.shared.b16 {%0, %1, %2, %3}, [%4];": "=r"(REG(dst[0])), "=r"(REG(dst[2])), "=r"(REG(dst[4])), "=r"(REG(dst[6])): "l"(__cvta_generic_to_shared(addr)));
}__device__ __forceinline__ void ldmatrix_trans_sync(half* dst, void* addr){asm volatile("ldmatrix.sync.aligned.x4.m8n8.shared.trans.b16 {%0, %1, %2, %3}, [%4];": "=r"(REG(dst[0])), "=r"(REG(dst[2])), "=r"(REG(dst[4])), "=r"(REG(dst[6])): "l"(__cvta_generic_to_shared(addr)));
}__device__ __forceinline__ void mma_sync_m16n8k16(half* c, half* a, half* b){asm volatile("mma.sync.aligned.m16n8k16.row.col.f16.f16.f16.f16 {%0, %1}, {%2, %3, %4, %5}, {%6, %7}, {%8, %9};": "=r"(REG(c[0])), "=r"(REG(c[2])): "r"(REG(a[0])), "r"(REG(a[2])), "r"(REG(a[4])), "r"(REG(a[6])), "r"(REG(b[0])), "r"(REG(b[2])), "r"(0), "r"(0));
}__device__ __forceinline__ void stmatrix_sync(half* dst, half* src){// ! Ampere doesn't have stmatrix.sync, we should simulate ituint64_t private_addr = (uint64_t)dst;uint64_t shared_addr[4];#pragma unrollfor(int i = 0; i < 4; ++i){shared_addr[i] = __shfl_sync(0xFFFFFFFF, private_addr, i * 8 + threadIdx.x / 4);}#pragma unrollfor(int i = 0; i < 4; ++i){*(reinterpret_cast<half2*>(shared_addr[i]) + threadIdx.x % 4) = HALF2(src[2 * i]);}
}/**
* \tparam S: SShift, right shift the addr for swizzling
* \tparam B: BShift, bits to be swizzled
* \tparam M: MBase, bits keep the same
*/
template <uint32_t S, uint32_t B, uint32_t M>
__device__ __forceinline__ uint32_t swizzle(uint32_t addr){constexpr auto Bmask = ((1 << B) - 1) << M;return ((addr >> S) & Bmask) ^ addr;
}__global__ void shared_memory_mma_swizzle_kernel(half* A, half* B, half* C){__shared__ half smem_a[16 * 16];__shared__ half smem_b[16 * 16];__shared__ half smem_c[16 * 16];// swizzle load A and Bint tx = threadIdx.x;// each thread load 8 bytes, so tx * 8 is the offsetuint32_t gAddr = tx * 8;auto g2sAddr = swizzle<3, 1, 3>(gAddr);LDST128BITS(smem_a[g2sAddr]) = LDST128BITS(A[gAddr]);LDST128BITS(smem_b[g2sAddr]) = LDST128BITS(B[gAddr]);__syncthreads();wmma::fragment<wmma::matrix_a, 16, 16, 16, half, wmma::row_major> a_frag;wmma::fragment<wmma::matrix_b, 16, 16, 16, half, wmma::row_major> b_frag;wmma::fragment<wmma::accumulator, 16, 16, 16, half> c_frag;wmma::fill_fragment(c_frag, 0.0f);// swizzle load frag a and buint32_t rAddr = (tx % 16) * 16 + (tx / 16) * 8;auto r2sAddr = swizzle<3, 1, 3>(rAddr);ldmatrix_sync(a_frag.x, smem_a + r2sAddr);ldmatrix_trans_sync(b_frag.x, smem_b + r2sAddr);// calc and storemma_sync(c_frag, a_frag, b_frag, c_frag);// store can also be swizzle, but we are interested in LDSM only// __syncthreads();// wmma::store_matrix_sync(smem_c, c_frag, 16, wmma::mem_row_major);// LDST128BITS(C[tx * 8]) = LDST128BITS(smem_c[tx * 8]);stmatrix_sync(smem_c + r2sAddr, c_frag.x);LDST128BITS(C[gAddr]) = LDST128BITS(smem_c[g2sAddr]);
}void shared_memory_mma_swizzle(half* A, half* B, half* C, int M, int N, int K){dim3 block(32);dim3 grid(1);shared_memory_mma_swizzle_kernel<<<grid, block>>>(A, B, C);
}int main(int argc, char* argv[]){// M = 16, N = 16, K = 16, warmup_iterations = 1,// profiling_iterations = 10, sleep_duration = 100, enable_check = falseTester tester(16, 16, 16, 1, 10, 100, true);tester.evaluate(shared_memory_mma_swizzle, "shared_memory_mma_swizzle");return 0;
}

与 V4 版本的 MMA 代码的核心差异体现在这里使用了 swizzle 实现地址重映射机制。下面我们从 swizzle 函数的底层逻辑、地址变换的具体过程、以及数据加载/访问的修改三个层面，详细分析它是如何工作的：(from doubao)

一、swizzle 模板函数的底层实现

swizzle 函数是解决 bank conflict 的核心，其通过 位运算对内存地址进行重映射，本质是交换地址中特定的比特位，从而改变数据在共享内存中的存储位置和访问路径。

1. 函数定义与参数

template <uint32_t S, uint32_t B, uint32_t M>
__device__ __forceinline__ uint32_t swizzle(uint32_t addr){constexpr auto Bmask = ((1 << B) - 1) << M;  // 生成用于位交换的掩码return ((addr >> S) & Bmask) ^ addr;         // 核心位运算：交换特定比特位
}

• 模板参数含义：
  • S（SShift）：地址右移的位数，用于需要选择交换的“源比特位”
  • B（BShift）：需要交换的比特位宽度（通常为 1，即交换 1 个比特）
  • M（MBase）：保持不变的基础比特位起始位置，高于此位置的比特位可能被交换
• 核心逻辑：通过 “右移 + 与掩码 + 异或” 的组合，交换 addr 中特定的比特位，生成重映射后的地址

2. 位运算的具体过程（以swizzle<3,1,3> 为例）

代码中实际调用的是 swizzle<3,1,3>(addr)，我们以这个实例来拆解位运算过程：

• 步骤 1：计算 Bmask
  • 代入 B=1, M=3：Bmask = ((1 << 1) - 1) << 3 = (1) << 3 = 8（二进制为 1000）
  • 作用：标记需要交换的目标比特位（此处为第 3 位，bit3，从 0 开始计数）
• 步骤 2：提取源比特位
  • (addr >> S) & Bmask 中，S=3 表示将 addr 右移 3 位，再与 Bmask（1000）做与运算，最终提取的是 addr 的 第 6 位（bit6）
• 步骤 3：异或实现比特交换
  • ((addr >> S) & Bmask) ^ addr 表示将提取的源比特位（bit6）与目标比特位（bit3）进行异或，实现二者的交换
  • bit6 是开关，bit3 是被翻转的目标
  • 开关关（bit=0）：bit0 保持原样
  • 开关开（bit6=1）：bit3 翻转一次
  • bit6 自己从头到尾不变

3. 实例：地址变换前后的比特变化

那上述解释有些抽象，我们来举个例子，目前 warp 内的 32 个线程在加载 global memory 中 16x16 矩阵时的访问图如下：

我们实际期望 warp 内的 32 个线程加载数据到 shared memory 时的位置排布如下：

为此我们要通过 swizzle<3,1,3> 这个模板函数实现，我们以 T0-T15 为例，计算 T0-T15 的 gAddr 和变换后的 g2sAddr（共享内存地址），结合二进制分析：

线程	tx	gAddr（十进制）	gAddr（二进制，低 7 位）	bit6 值	bit3 值	swizzle 后 g2sAddr（十进制）	变化结果
T0	0	0	0000000	0	0	0	不变
T1	1	8	0001000	0	0	8	不变
T2	2	16	0010000	0	0	16	不变
T3	3	24	0011000	0	1	24	不变
T4	4	32	0100000	0	0	32	不变
T5	5	40	0101000	0	1	40	不变
T6	6	48	0110000	0	0	48	不变
T7	7	56	0111000	0	1	56	不变
T8	8	64	1000000	1	0	72 (1001000)	与 T9 互换
T9	9	72	1001000	1	1	64 (1000000)	与 T8 互换
T10	10	80	1010000	1	0	88 (1011000)	与 T11 互换
T11	11	88	1011000	1	1	80 (1010000)	与 T10 互换
T12	12	96	1100000	1	0	104 (1101000)	与 T13 互换
T13	13	104	1101000	1	1	96 (1100000)	与 T12 互换
T14	14	112	1110000	1	0	120 (1111000)	与 T15 互换
T15	15	120	1111000	1	1	112 (1110000)	与 T14 互换

以线程 T8 为例：

addr = 64
二进制 (7位) = 1000000↑bit6
bit6 = 1
bit3 = 0

• Bmask = 0001000
• ((addr >> S) & Bmask) = ((1000000 >> 3) & 0001000) = (0001000 & 0001000) = 0001000
• ((addr >> S) & Bmask) ^ addr = 0001000 ^ 1000000 = 1001000 = 72
• 口诀：bit6 是开关，bit3 是被翻转的目标
  • bit6=1，开关开
  • bit3=0，被翻转
  • bit6=1，bit3=0
  • 最终结果：1001000=72

我们可以简单 Debug 验证下，如下图所示：

我们从上图可以清晰的看到，对于线程 T8，在未转换之前的地址是 64（gAddr），经过 swizzle<3,1,3> 转换之后的地址变成了 72（g2sAddr），和我们前面分析的一样

在上表中 T0-T7 线程地址不变，T8-T15 线程地址互换，原因是：

• T0-T7：gAddr 最大为 56（二进制 0111000），bit6 值为 0（因 64=2^6 > 56），翻转开关始终关闭，bit3 值不变，所以地址不变
• T8-T15：gAddr 范围 64-120，bit6 值为 1（因 64=2^6 ≤ 地址），翻转开关始终打开，此时：
  • 若原 bit3 值为 0（如 T8、T10、T12、T14），替换后 bit3=1，地址 + 8
  • 若原 bit3 值为 1（如 T9、T11、T13、T15），替换后 bit3=0，地址 - 8
  • 因此形成相邻线程的地址互换

二、数据加载阶段的地址变换（全局内存→共享内存）

V4 版本代码中，全局内存到共享内存的加载是 线性映射（smem_a[tx * 8] = A[tx * 8]），而上面带 swizzle 版本代码通过 g2sAddar 实现了地址重映射：

// 带Swizzle的代码：全局内存→共享内存的加载
uint32_t gAddr = tx * 8;                  // 全局内存地址（原始线性地址）
auto g2sAddr = swizzle<3, 1, 3>(gAddr);  // 重映射后的共享内存地址
LDST128BITS(smem_a[g2sAddr]) = LDST128BITS(A[gAddr]);  // 使用变换后地址存储

1. gAddr 的含义

gAddr = tx * 8：每个线程加载 8 个 half 元素（共 16 字节，LDST128BITS 是 128 位加载），tx（0~31）对应 32 个线程，总加载量为 32 * 8 = 256 个 half，正好填满 16 * 16 的共享内存

2. g2sAddr 如何改变共享内存布局

通过 swizzle<3,1,3> 变换后，g2sAddr 的值与 gAddr 不同，导致全局内存中的数据块被 打乱 后存入共享内存，如 Figure 2 所示

这种 打乱 使得共享内存中相邻地址的数据不再来自全局内存的连续块，从而改变了数据的 bank 分布

三、共享内存→寄存器（Fragment）的地址变换

V4 版本代码中，从共享内存加载数据到 a_frag/b_frag 使用线性地址（smem_a + row*16 + col*8），而带 swizzle 版本的代码通过 r2sAddr 实现了地址重映射

// 带Swizzle的代码：共享内存→Fragment的加载
uint32_t rAddr = (tx % 16) * 16 + (tx / 16) * 8;  // 原始共享内存访问地址
auto r2sAddr = swizzle<3, 1, 3>(rAddr);           // 重映射后的访问地址
ldmatrix_sync(a_frag.x, smem_a + r2sAddr);         // 使用变换后地址加载

1. rAddr 的含义

uint32_t rAddr = (tx % 16) * 16 + (tx / 16) * 8;

• tx % 16：线程在 16 行中的行索引（0~15）
• tx / 16：线程在列方向的分组索引（0 或 1）
• 整体表示线程需要从共享内存加载数据的原始地址

2. r2sAddr 如何避免 bank 冲突

r2sAddr 是 rAddr 经 swizzle<3,1,3> 变换后的地址，变换规则和前面 g2sAddr 一致，这边博主就不再赘述了，其作用是让线程访问共享内存时，地址的低 5 位（bank 索引）分散开，如 Figure 2 所示

ncu 分析的结果如下所示：

我们可以清晰的看到，经过 swizzle 方法之后的 bank conflict 问题被完全解决了

5. swizzle 实现思路讲解

在上小节中我们分析了 swizzle 的原理，并通过代码实现了利用 swizzle 来解决 bank conflict 问题

不知道大家有没有困惑，swizzle 函数是怎么设计的呢？为什么给定的 swizzle 参数是 <3,1,3> 就能解决我们当前场景的 bank conflict 问题呢，如果是其它场景参数又该如何指定呢？🤔

要理解 swizzle<3,1,3> 参数的由来，以及如何根据实际的 bank conflict 场景选择合适的参数，需要从 bank conflict 的本质和位运算对地址分布的影响 两个核心维度分析。下面我们分步骤拆解参数设计的逻辑，并总结通用的参数选择方法：(from doubao)

一、先明确 bank conflict 的本质是 “地址低 5 位重复”

GPU 共享内存的 bank 索引由地址的 低 5 位（bit0~bit4）决定（因为 32 个 bank，2^5=32）。当多个线程地址满足 addr1 % 32 == addr2 % 32 == ... 即低 5 位完全相同，就会产生 bank conflict

因此，swizzle 的核心目标是：通过位运算修改地址的低 5 位，打破这种重复性，使原本冲突的地址在低 5 位上产生差异

二、swizzle<3,1,3> 参数的由来（结合当前场景）

在 V4 版本代码中，原始地址（gAddr = tx * 8）的低 5 位存在 周期性重复，这是导致冲突的根源。我们先来分析原始地址的低 5 位模式，再看参数如何针对性解决

1. 原始地址的低 5 位模式（导致冲突的关键）

每个线程的 gAddr = tx * 8（tx = 0~31），换算成低 5 位（bit0~bit4）的二进制如下：

• T0（tx = 0）：0 → 低 5 位 00000
• T1（tx = 1）：8 → 低 5 位 01000（bit3=1）
• T2（tx = 2）：16 → 低 5 位 10000（bit4=1）
• T3（tx = 3）：24 → 低 5 位 11000（bit4=1，bit3=1）
• T4（tx = 4）：32 → 低 5 位 00000（与 T0 重复）
• T5（tx = 5）：40 → 低 5 位 01000（与 T1 重复）
• …
• T8（tx = 8）：64 → 低 5 位 00000（与 T0、T4 重复）
• T9（tx = 9）：72 → 低 5 位 01000（与 T1、T5 重复）

规律：地址的低 5 位以 00000→01000→10000→11000 为周期性重复（周期为 4），导致大量线程的低 5 位完全相同（如 T0、T4、T8 的低 5 位都是 00000），必然产生严重 bank conflict

2. 为什么选择 S=3, B=1, M=3?

参数的设计目的是 打破低 5 位的周期性重复，具体针对上述模式：

• M = 3：表示 “从 bit3 开始的位需要被修改”。观察原始地址的低 5 位，冲突的核心是 bit 的取值（00000 中 bit3=0，01000 中 bit3=1），因此选择 bit3 作为 “目标修改位”（M = 3 即 bit3）
• B = 1：表示 “只需要修改 1 个比特位”。因为冲突的根源是 bit3 的周期性重复（每 4 个线程重复一次），修改这 1 位即可打破周期，无需修改多位
• S = 3：表示 “源比特位是 bit3+3=bit6”。需要找一个 “与 bit3 取值不相关” 的比特作为源（避免修改后仍有重复）。在当前场景的地址中，bit6 的取值规律与 bit3 完全不同（bit6 在 tx=8~15 时为 1，tx<8 或者 tx≥16 时为 0），用 bit6 的值替换 bit3，可彻底打破低 5 位的重复模式

3. 效果验证

替换后，低 5 位的 bit3 被 bit6 的值覆盖：

• T0（bit6=0）：bit3=0→低 5 位仍 00000（但 T4、T8 的 bit6 不同，低 5 位不再重复）
• T8（bit6=1）：bit3=1→低 5 位变为 01000（与原始 T1 的低 5 位相同，但 T0、T4 的低 5 位已不同，冲突消除）

最终，低 5 位的周期性被打破，bank conflict 解决

三、通用方法：如何根据实际应用场景设计 swizzle 参数？

当遇到 bank conflict 时，可以按照下步骤推导 swizzle 参数 (S, B, M)：

步骤 1：分析冲突地址的低 5 位模式

首先通过 Night Compute 等工具定位 哪些地址导致了冲突（例如，记录冲突的地址列表：addr1, addr2, ...），然后提取这些地址的低 5 位（bit0~bit4），找出它们的 共同规律：

• 是 bit2 重复？还是 bit3~bit4 的组合重复？
• 重复周期是多少（如每 2 个、4 个、8 个地址重复一次）

例如，若发现冲突地址的 bit2 总是相同（如 xx0xx），则 bit2 是需要修改的关键位。

步骤 2：确认 “目标位置” （M 和 B）

• M：需要修改的起始比特位（在低 5 位内，通常是导致重复的核心位）。例如，若 bit2 重复，则 M=2。
• B：需要修改的比特位数（通常为 1，除非多位联合导致重复）。若仅 bit2 重复，B=1；若 bit2~bit3 的组合重复，B=2。

步骤 3：确认 “源比特位” （S）
源比特位需要满足：其取值规律与目标位完全不同（避免修改后仍有重复）。

• 源比特位的位置 = M + S（S是右移的位数，即源位比目标位高S位）。
• 选择原则：源比特位在冲突地址中的取值应 “随机化”（与目标位无关联）。

例如，若目标位是 bit2（M=2），发现 bit5 的取值与 bit2 完全无关（bit2=0 时 bit5 可能为 0 或 1），则源位是 bit5，S=5-2=3（因为 M + S = 2 + 3 = 5）。

步骤 4：验证与调整
用设计的参数生成变换后的地址，检查低 5 位是否还存在重复：

• 若仍有冲突，说明源位选择不当（与目标位仍有关联），需换一个源位（调整 S）。
• 若冲突消除，则参数有效。

四、举例：另一种冲突场景的参数设计

假设遇到新的冲突：

• 冲突地址的低 5 位中，bit1~bit2 的组合总是 00（即 xx00x），导致重复。
• 分析发现 bit4~bit5 的组合取值随机（与 bit1~bit2 无关）。

参数设计：

• B=2（需要修改 2 个比特位：bit1~bit2）。
• M=1（从 bit1 开始修改）。
• S=3（源位是 bit1+3+bit4+bit5，因为 M + S = 1 + 3 =4）。

最终参数：swizzle<3, 2, 1>, 通过对 bit4~bit5 的值替换 bit1~bit2，打破重叠模式。

总结

swizzle 参数 S, B, M 设计是 针对性解决地址低 5 位重复问题 的工具：

• M 和 `B 定位 “需要修改的关键位”（导致冲突的根源）。
• S 选择 “能打破重复的源位”（与关键位无关联）。

当前场景中，swizzle<3,1,3>恰好针对 “bit3 重复” 且 “bit6 与 bit3 无关” 的特点，因此能解决冲突。实际开发中，需先分析冲突地址的位模式，再按上述步骤推导参数，核心是 “让修改后的低 5 位不再重复”。

OK，以上就是整篇文章的全部内容了，如果大家还对 swizzle 有所困惑可以多看看 UP 主的视频或者看看 UP 主推荐的文章 实用 Swizzle 教程（一）

结语

这篇文章我们学习了 wmma 中 bank conflict 产生的原因以及解决方法，产生的主要原因（以组别 1 为例）是 mma 指令 ldmatrix 从 shared memory 加载数据到寄存器 fragment 中时 addr4-addr7 地址访问的 bank 与 addr0-addr3 访问的 bank 相同，从而产生了 bank conflict 问题

关于 bank conflict 的解决方法我们先学习了通过 padding 的方式来解决，通过在 shared memory 中 padding 8 列从而打破原有 bank 分布，但这种方式会多申请 shared memory 资源，造成浪费和带宽利用率降低

接着我们学习了通过 swizzle 方法即地址重映射来巧妙的解决 bank conflict 问题，最后我们学习了 swizzle 的原理，还学习了 swizzle 实现的思路和一些技巧

总的来说，这个系列还是学到了很多知识的，感谢 UP 主的分享，大家感兴趣的可以多看看 up 主的视频，还是非常不错的🤗

下载链接

• MMA 与 Swizzle 代码下载链接【提取码：1234】

参考

• https://docs.nvidia.com/cuda/parallel-thread-execution/#warp-level-matrix-instructions-for-mma
• 【CUDA进阶】MMA分析Bank Conflict与Swizzle（已完结）
• https://github.com/xlite-dev/LeetCUDA
• https://github.com/Bruce-Lee-LY/cuda_hgemm
• https://github.com/Chtholly-Boss/swizzle
• https://chatgpt.com
• Nvidia Tensor Core-CUDA HGEMM优化进阶
• 实用 Swizzle 教程（一）