2024年INS SCI2区，基于快速成本评估和蚁群优化算法的多无人地面飞行器分层任务规划，深度解析+性能实测

---

1.摘要

多无人地面车辆（multi-UGV）任务规划是实现车队自主协同的核心环节，然而该问题因子任务间的高度耦合及复杂环境的不确定性而具有较大挑战。针对这一问题，本文提出了一种分层任务规划算法架构，其包括基于双层环境建模改进代价近似方法，用于快速估算目标点的行进代价图；融合 k-means聚类与边际代价分配混合聚类方法，用于高效任务分解与分派；以及集成A* 算法、路径后处理与多算子连续蚁群优化算法的三层路径规划方法，用于在复杂地形中生成低代价路径。

2.多UGV任务规划描述

在多UGV任务规划问题中，设目标点集合为T={T1,...,Ti,...,TNt}T=\{T_{1},...,T_{i},...,T_{N_{t}}\}T={T1​,...,Ti​,...,TNt​​}，UGV集合为U={U1,...Uu,...,UNu}U=\{U_{1},...U_{u},...,U_{N_{u}}\}U={U1​,...Uu​,...,UNu​​}，该问题核心目标是在保证所有目标点均被访问的前提下，规划出一组可行方案，使任务总成本最小化。

任务分解与分配

多UGV任务规划可视为将目标点集合划分为若干子集，并分配给不同UGV以最小化任务成本。在假设UGV同质且电量充足的条件下，该问题建模为任务分解问题的变体，其解为一组互不相交且覆盖全部目标点的子集，每个子集由唯一UGV执行，允许部分UGV未被分配任务。

任务排序

在已分配的目标点子集${\varphi }_q$及各目标点之间行进代价已知情况下，任务排序变为TSP问题。其目标是在已分配的目标点子集内，为每台UGV确定一条访问顺序，使总行进代价最小。
$$\min F_{sub}^u=\sum _{i=1}^{N_t^u}\sum _{j=1,j\ne i}^{N_t^u}T{C}_{ij}\cdot {\psi }_{ij}^u$$

路径规划

路径规划在满足约束条件前提下，为UGV寻找从起始位置到目标位置的路径，并最小化行进代价。论文考虑路径代价、转向代价，碰撞代价采用罚函数形式：
$$TC={\alpha }_1\cdot C_{length}+{\alpha }_2\cdot C_{turning}+C_{collision}$$

3.多UGV任务规划系统

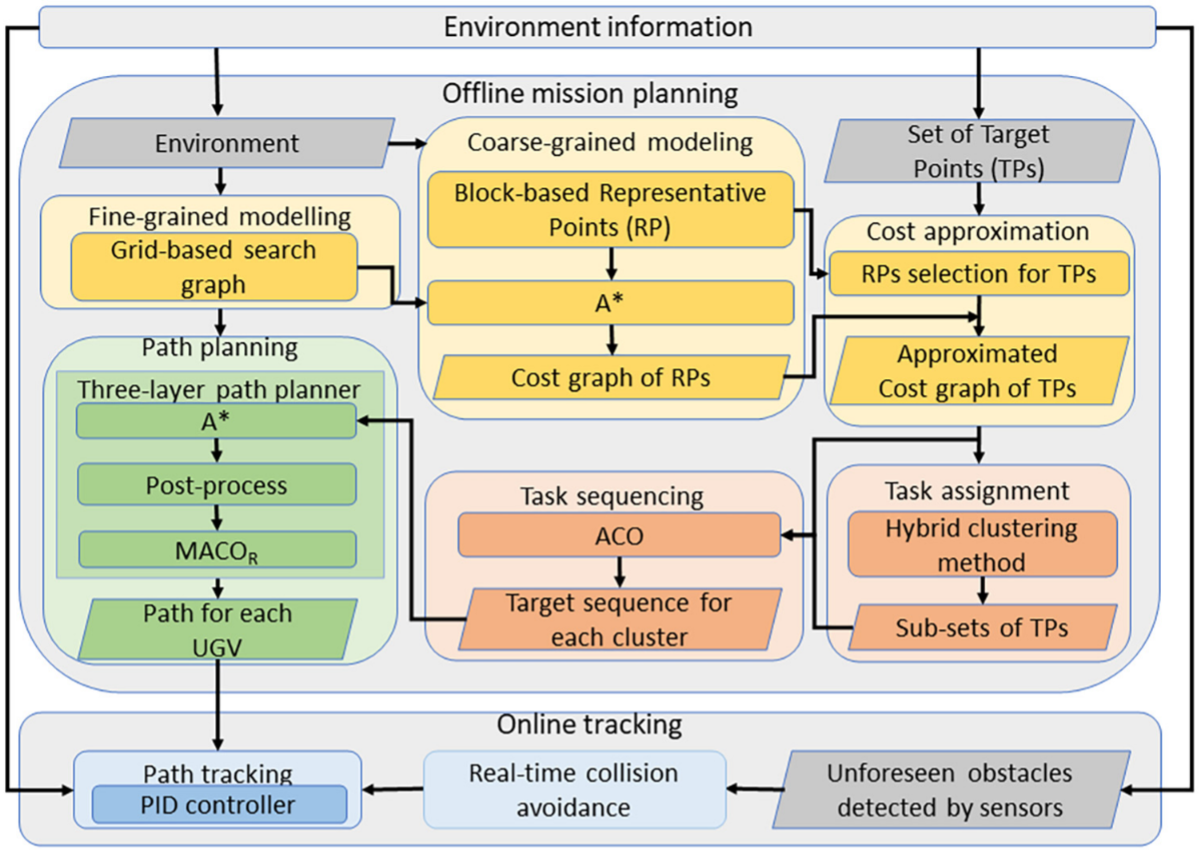
本文构建了一个多UGV任务规划系统，由环境建模（黄色）、任务规划（橙色）与路径规划（绿色）三大模块组成。系统在障碍物密集的部分可观测环境下，先通过环境建模提取特征并生成搜索图，再支持任务与路径规划优化，最终将结果传递至跟踪系统完成执行。

双层环境建模

为支持任务规划与路径规划，本文引入了双层环境建模方法，包括精细建模与粗粒度建模，提出了改进近似方法。

• 精细建模层：基于网格的A* 路径规划构建搜索图，并识别网格连通性；
• 粗粒度建模层：利用精细建模所得信息，从环境中选取代表点（RPs），并建立可复用的RPs行进代价图，以快速评估任意两个目标点间的行进代价。

面向任务分解与分配混合聚类方法

本文在任务规划中提出了一种混合聚类方法（HCM），将改进 k-means 聚类与基于边际代价的分配相结合，实现任务分解与分配方法集成。该方法以近似行进代价替代欧氏距离进行聚类，并通过代表点（RP）加速代价评估；同时利用边际代价准则对初始聚类结果进行调整，从而减少跨聚类路径交叉，提升整体任务分配效率与路径质量。

三层路径规划方法

本质分为三步A* 快速生成可行路径、去冗余、MACOR优化。

4.结果展示

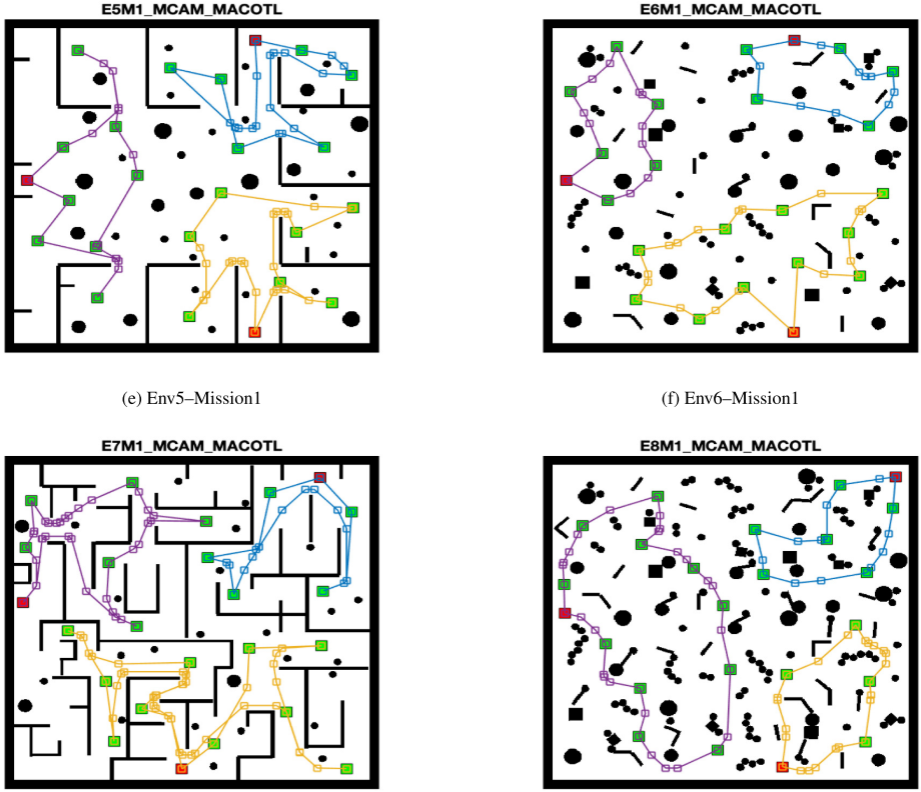
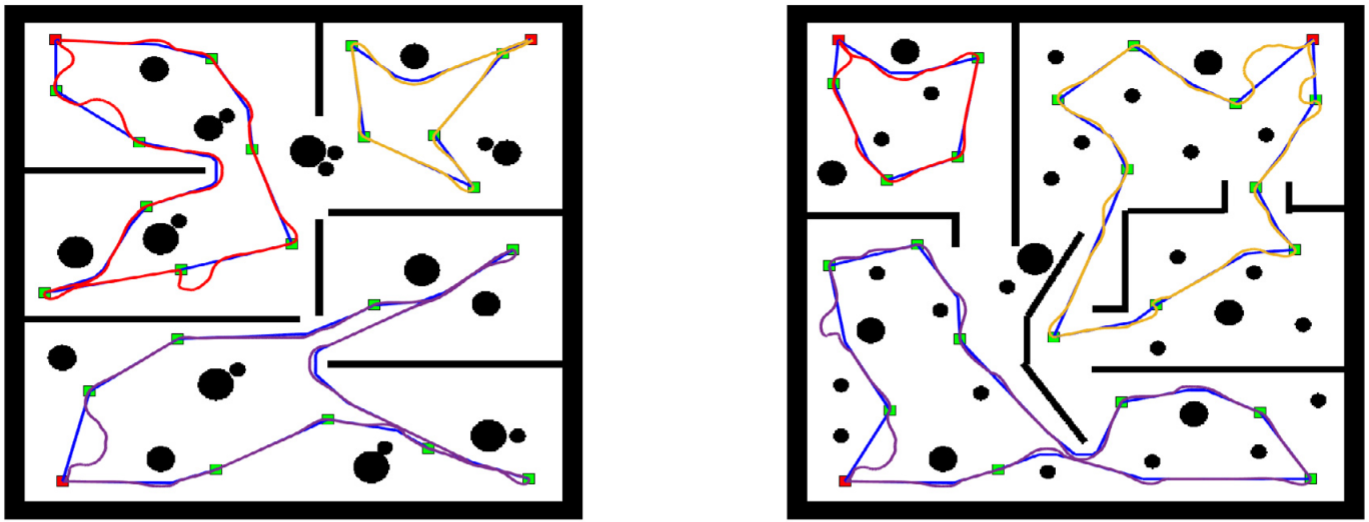
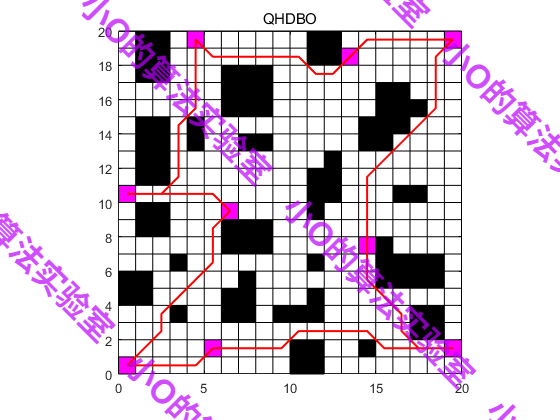
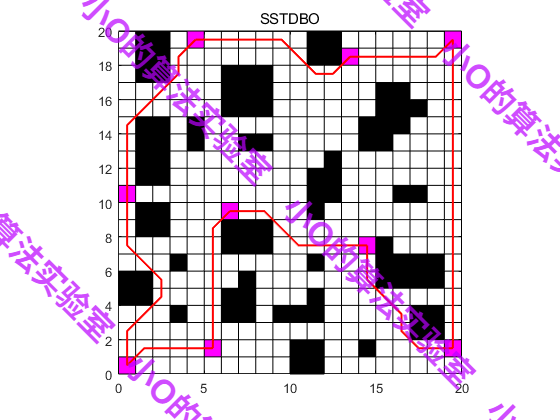
5.参考文献

[1] Liu J, Anavatti S, Garratt M, et al. A hierarchical mission planning system for multi-uncrewed ground vehicles using fast cost evaluation and ant colony optimisation[J]. Information Sciences, 2024, 679: 121029.

6.代码获取

xx

7.算法辅导·应用定制·读者交流

xx