牛客网 DP35 二维前缀和

一、问题描述

二、解题思路

整体思路

本题可以用二维前缀和矩阵来解决。

具体思路

定义：dp[i][j]表示从(1,1)位置到(i,j)位置，这段区间内所有元素的和(本题前缀和数组从下标1开始)

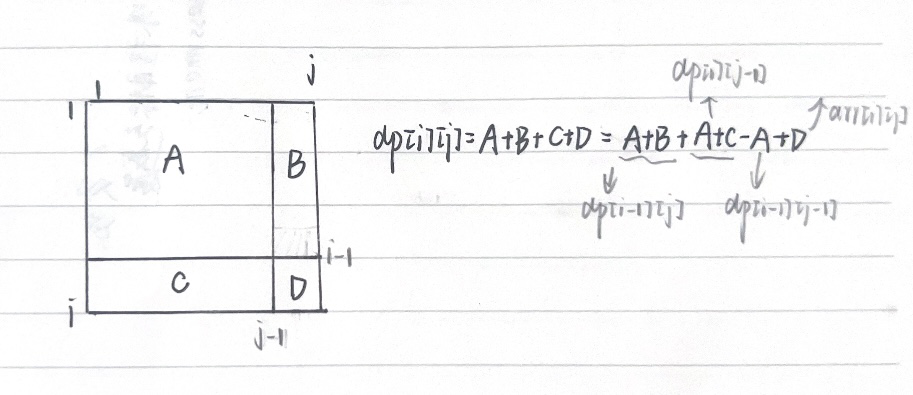
(1)构造二维前缀和矩阵，如图所示

dp[i][j]=A+B+C+D=(A+B)+(A+C)-A+D=dp[i-1][j]+sp[i][j-1]-dp[i-1][j-1]+arr[i][j]

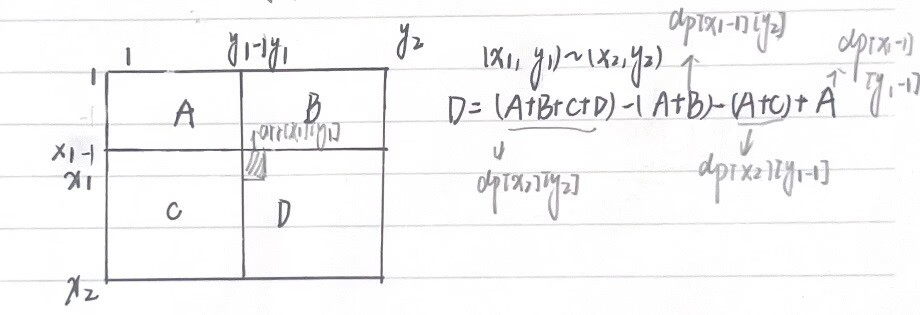
(2)使用二维前缀和矩阵，如图所示

(x1,y1)~(x2,y2):

D=(A+B+C+D)-(A+B)-(A+C)+A=dp[x2][y2]-dp[x1-1][y2]-dp[x2][y1-1]+dp[x1-1][y1-1]

三、代码实现

时间复杂度：T(n)=O(m*n+q)

空间复杂度：S(n)=O(m*n)

#include <iostream>
#include <vector>
using namespace std;int main() {int m,n,q;cin>>m>>n>>q;vector<vector<long long>> arr(m+1,vector<long long>(n+1,0));for(int i=1;i!=m+1;i++)for(int j=1;j!=n+1;j++)cin>>arr[i][j];//构造前缀和矩阵vector<vector<long long>> dp(m+1,vector<long long>(n+1,0));for(int i=1;i!=m+1;i++)for(int j=1;j!=n+1;j++)dp[i][j]=dp[i-1][j]+dp[i][j-1]-dp[i-1][j-1]+arr[i][j];//使用前缀和矩阵while(q--){int x1,y1,x2,y2;cin>>x1>>y1>>x2>>y2;long long result=dp[x2][y2]-dp[x1-1][y2]-dp[x2][y1-1]+dp[x1-1][y1-1];cout<<result<<endl;}
}