当前位置：首页 > news >正文

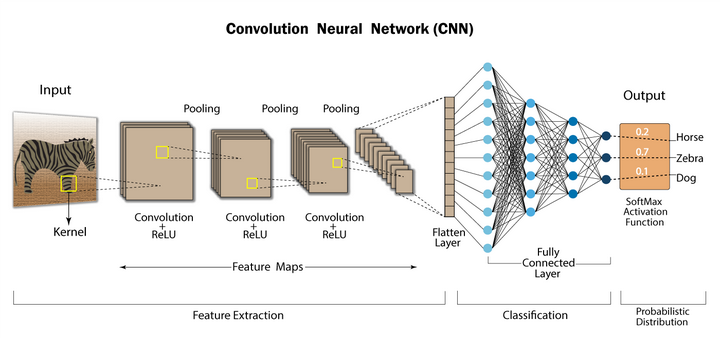
一天认识一个神经网络之--CNN卷积神经网络

news 2025/8/29 12:04:50

CNN 是一种非常强大的深度学习模型，尤其擅长处理像图片这样的网格结构数据。你可以把它想象成一个系统，它能像我们的大脑一样，自动从图片中学习并识别出各种特征，比如边缘、角落、纹理，甚至是更复杂的物体部分（比如眼睛或者车轮）。

CNN如何看图？

可以把CNN“看”图的过程想象成一个侦探在分析一张照片

寻找基础线索 (Detecting Basic Features): 最开始，CNN就像一个拿着放大镜 🔎 的侦探。它不会立刻去看整张图，而是逐个小区域地扫描，寻找最基础的线索，比如边缘、角落、颜色变化等。这些是构成任何图像最基本的元素。
组合线索 (Combining Features): 接下来，CNN会把上一步找到的基础线索组合起来。比如，它可能会发现“一条曲线”和“另一条曲线”经常一起出现，构成了一个“圆形”的图案；或者某些线条组合起来像一种“纹理”。
形成整体概念 (Recognizing Objects): 更深一层的CNN会把这些组合好的图案（比如圆形、纹理）进一步组装成更复杂的概念。它会学习到，“一个圆形”加上“两个倒三角形”可能就代表了一张“猫脸” 🐈。
最终判断 (Classification): 最后，在收集了所有这些从简单到复杂的证据之后，CNN会综合所有信息，给出一个最终的判断：“根据我看到的所有特征，我95%确定这是一张猫的图片。”

卷积层 (Convolutional Layer)

卷积层工作方式可以分为三个关键部分：

滤波器/核 (Filter / Kernel): 这就是“放大镜”的镜片。它其实是一个很小的数字矩阵（比如 3x3 大小），被设计用来识别一个特定的微小特征。例如，会有一个专门用来找“垂直边缘”的滤波器，一个专门找“水平边缘”的滤波器，还有一个可能专门找“绿色”的滤波器。
滑动计算 (Convolution): CNN会拿着这个滤波器，在原始图片的左上角盖住一小块区域。它将滤镜上的数字与图片上对应位置的像素值相乘再相加，得到一个新的数字。然后，它就像移动窗户一样，将滤镜向右滑动一格，重复计算，再向右……直到扫完整张图片。
特征图 (Feature Map): 每当滤波器在一个区域发现它要找的特征时（比如，“垂直边缘”滤镜找到了一个垂直边缘），计算出的那个新数字就会很大。反之，如果没找到，数字就很小。所有这些新数字组合在一起，就形成了一张新的“图”，我们称之为特征图。这张图就像一张“证据地图”，清晰地标示出了原始图片中哪里有我们想找的那个特定特征。

假设我们有一张 5×5 的灰度图像，可以想成是一个 5×5 的矩阵，每个元素代表像素值。

我们再有一个 3×3 的卷积核（kernel/filter），也就是一个 3×3 的小矩阵。

卷积的步骤：

把这个 3×3 核心，放在图像左上角的 3×3 区域。
对应元素相乘，再求和 → 得到一个数。
把核往右挪一个像素（stride=1），重复上面过程。
一直滑动，直到整张图都“扫描”完。

最终得到的，不再是 5×5，而是一个更小的矩阵（这里会是 3×3，我们马上会推导）。

为什么会变小？

规律是这样的：如果输入大小是 N×N，卷积核大小是 K×K，stride=1，不加 padding，输出大小就是：

(N−K+1)×(N−K+1)

套到刚才的例子：输入 = 5×5 卷积核 = 3×3 → 输出 = (5 - 3 + 1) × (5 - 3 + 1) = 3 × 3

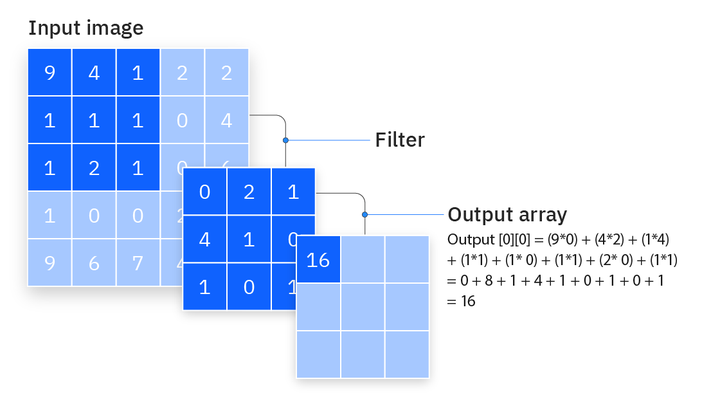
多通道卷积是怎么计算的？

刚才的例子，我们是从单通道的灰度图像举例的。

对于灰度图：

输入是一张 5×5 矩阵（单通道）。
卷积核是 3×3，结果也是一个矩阵。

但是，在实际运用中，输入往往是RGB三通道的彩色图像：

输入大小=3×H×W （3 表示通道数：红、绿、蓝）。

多通道卷积的关键：

每个卷积核的大小是 input_channels×k×k。
例如输入有 3 个通道，卷积核大小为3*3，卷积核就是 3×3×3。
卷积时，每个通道单独卷积，得到 3 个结果矩阵，然后把它们相加 → 得到一个最终的特征图。
每个卷积核都会生成 1 张特征图。
有多少个卷积核，就会输出多少个通道。

👉 举个例子：

输入：大小 3×32×32（一张 RGB 小图）。
卷积层：nn.Conv2d(in_channels=3, out_channels=8, kernel_size=3)。
结果：输出 8×30×30。
（8 表示我们学到了 8 个特征图，每个是 30×30）。

相信大家都想到了一个核心问题：同一个卷积核在不同通道上是不是一样的？

答案：不是一样的。

对于一个3*3*3的卷积核为例：

每一个通道上的核的权重是不一致的，也就是说，一共有三个不同权重的大小为3*3的核。分别对应输入的 3 个通道。

卷积时，不同的核和对应通道做卷积 → 得到 3 张中间结果。

然后把这 3 张结果逐元素相加 → 得到最终的 1 张输出特征图。

如何设计卷积核？

但在CNN中，这些Filter的值是网络自己学习到的。

这个过程是这样的：

1. 随机初始化 (Random Initialization): 在训练开始之前，我们根本不知道哪些Filter是最好的。所以，我们就用一堆随机的、很小的数字来填充所有的Filter。在这一阶段，这些Filter是“无知”的，它们提取出的特征图也基本是无意义的噪声。
2. 前向传播与计算误差 (Forward Pass & Calculate Error): 我们给网络看一张图片，比如一张猫的图片，并且告诉它“这是一只猫”。网络会用它那些随机的Filter去处理这张图，经过一系列计算后，它会给出一个预测。因为Filter是随机的，它的第一次预测很可能错得离谱，比如它可能会说：“我有10%的把握这是猫，90%的把握这是狗”。然后，我们将这个离谱的预测和正确答案（100%是猫）进行比较，计算出一个“误差”或“损失”（Loss）。这个误差值衡量了网络这次“错得有多严重”。
3. 反向传播与更新Filter (Backpropagation & Update Filters): 这是最关键的一步。网络会使用一个叫做反向传播 (Backpropagation) 的算法，像一个侦探一样，从最终的误差开始，一层一层地往回追溯，计算出网络中每一个数字（包括所有Filter里的数值）对这个最终的误差“贡献”了多少。对于那些导致错误判断的Filter数值，算法会稍微调整它们，让它们朝着能减少误差的方向改变一点点。这个调整的过程通常使用一种叫做梯度下降 (Gradient Descent) 的优化方法。
4. 重复，重复，再重复: 网络会不断地重复以上过程：看一张图 -> 预测 -> 计算误差 -> 反向传播更新Filter。当我们把成千上万张猫和狗的图片都给它看过之后，神奇的事情就发生了：

第一层的Filter为了能有效区分猫和狗，会“自发地”学习到应该去检测一些最基础的特征，比如边缘、角落和颜色块，因为这些是所有物体共有的基础元素。
更深层的Filter则会学习如何组合这些基础特征，形成更复杂的纹理、形状，比如眼睛、耳朵的轮廓等。

总结一下：我们不设计Filter，我们只为网络设定一个目标（比如，正确分类图片），然后给它提供大量的数据和反馈（误差），网络就会在一次次的“试错”和“修正”中，自动学习出最优的Filter组合。

这个自动学习特征的能力，是CNN如此强大的根本原因。

池化层 (Pooling Layer)

在我们刚刚讨论的卷积层之后，我们得到了一堆“证据地图”（特征图）。这些图可能非常大，而且包含了很多冗余信息。

池化层的目的就很直接：对这些特征图进行“压缩提炼”，去粗取精。

它主要做两件事：

减小尺寸 (Downsampling): 大大减小特征图的尺寸，这样可以显著减少后续计算的负担，让网络运行得更快。
保持重要特征 (Feature Invariance): 保留每个小区域内最显著的特征，同时忽略一些不那么重要的细节。这让网络具有一定的“不变性”——即使图片中的物体有轻微的平移或形变，网络依然能够认出它。

最常用的一种池化方法叫做最大池化 (Max Pooling)。它的工作方式非常简单：

划定区域：像卷积一样，它也用一个小窗口（通常是 2x2 大小）来扫描特征图。
取最大值：在这个 2x2 的窗口覆盖的4个像素中，它只保留数值最大的那一个，把其他的都丢掉。
滑动窗口：然后，它将窗口移动到下一个区域（通常步长为2，也就是不重叠地移动），重复这个过程，直到扫完整张图。

举个例子：

假设我们有下面这个 4x4 的特征图，我们要用一个 2x2 的最大池化窗口来处理它。

添加图片注释，不超过 140 字（可选）

左上角 2x2 区域: [[1, 3], [4, 1]]，最大值是 4。
右上角 2x2 区域: [[5, 2], [8, 3]]，最大值是 8。
左下角 2x2 区域: [[6, 2], [2, 9]]，最大值是 9。
右下角 2x2 区域: [[1, 7], [3, 4]]，最大值是 7。

经过最大池化后，原来 4x4 的特征图就被压缩成了一个 2x2 的新特征图，只留下了每个区域最强的“信号”：

[4，9；8，7]

你看，尺寸大大减小了，但每个区域最关键的特征信息（那个最亮的点）被保留了下来。

到目前为止，我们已经了解了CNN的核心特征提取部分：

输入图片 -> [卷积层 -> 池化层] -> [卷积层 -> 池化层] -> ... -> 高度提炼的特征图

这个 [卷积 + 池化] 的组合可以重复多次，层数越深，提取的特征就越抽象、越高级。

在完成了所有这些特征提取之后，网络需要根据这些最终的特征图，做出最后的判断。

这里就要介绍全连接层 (Fully Connected Layer) 了。

全连接层 (Fully Connected Layer)

到目前为止，我们的CNN已经通过一系列的卷积和池化层，将原始图片转换成了一组高度提炼的特征图。这些特征图代表了图片中是否存在某些高级特征（比如“耳朵”、“眼睛”的轮廓等）。

但是，这些特征还是一些二维的“地图”，网络还不能直接用它们来做判断。全连接层的作用就是汇总所有证据，做出最终裁决。

这个过程分为两步：

1. 压平 (Flatten)

在进入全连接层之前，我们需要做一个简单的准备工作：压平 (Flatten)。

想象一下，我们把上一层输出的所有二维特征图，一个接一个地首尾相连，拉成一条长长的一维向量。

这个长向量就包含了图片中所有被检测到的高级特征的“清单”。

2. 全连接计算 (The Fully Connected Layers)

这个压平后的长向量，会被输入到一个或多个全连接层中。

“全连接”这个名字非常形象：

在这一层里，每一个神经元都和前一层的所有神经元（也就是那个长向量里的每一个值）相连接。
它的工作方式就像一个传统的神经网络。它会学习如何根据这个特征“清单”中的不同组合来进行打分。

继续用我们的侦探比喻：

卷积/池化层是负责搜集证据的侦探们，他们提交了各自的报告（特征图），说“我在这里发现了爪印”、“我在这里发现了胡须的纹理”。
压平操作就是把所有这些报告整理成一个大档案。
全连接层就是首席侦探，他会阅读整个档案，并根据所有证据的权重进行综合分析：“嗯... 既有胡须，又有尖耳朵，还有猫科动物的眼睛轮廓... 综合来看，这些特征组合在一起，指向‘猫’的可能性非常高。”

输出层 (Output Layer)

通常，最后一个全连接层的神经元数量，和我们要分类的类别数量是相等的。

比如，做一个猫狗二分类任务，最后就有2个神经元。
比如，做一个0-9的手写数字识别，最后就有10个神经元。

最后，我们通常会在这之上再加一个 Softmax 函数，它能将每个类别的最终得分，转换成一个概率值（所有概率加起来等于1）。这样，网络输出的就不是[猫得分: 2.8, 狗得分: 0.1]，而是更加直观的[猫的概率: 95%, 狗的概率: 5%]。

计算实例拆解全连接层

我们假设，经过了最后的卷积和池化层，再通过“压平”操作，我们得到了一个长度为4的特征向量。这在真实网络中会非常长（可能有几千个元素），但我们用一个短的来演示计算：

输入向量 (Input Vector): [2, 1, 3, 5]

这个向量可以理解为网络的“证据清单”：

第1个值 2：代表网络检测到的“尖耳朵”特征的强度。
第2个值 1：代表“胡须”特征的强度。
第3个值 3：代表“圆眼睛”特征的强度。
第4个值 5：代表“毛茸茸纹理”特征的强度。

现在，我们想把这个包含4个特征的向量，输入到一个拥有3个神经元的全连接层。我们的目标是，让这3个神经元分别对“猫”、“狗”、“其他”这三个类别打分。

一个全连接层包含两个需要学习的部分：权重 (Weights) 和偏置 (Biases)。

1. 权重 (Weights)

每个神经元都会对每一个输入特征分配一个权重。这个权重代表了该神经元有多“看重”这个输入特征。

一个大的正权重意味着：“如果这个特征很强，那么我就应该给出更高的分”。
一个大的负权重意味着：“如果这个特征很强，那么我就应该给出更低的分”。

因为我们有4个输入特征和3个神经元，所以我们会有一个 3x4 的权重矩阵：

Weights=

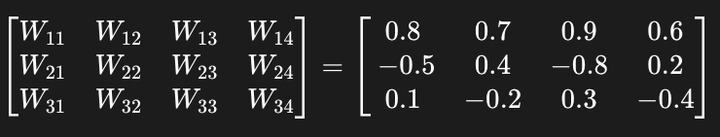
添加图片注释，不超过 140 字（可选）

第一行是“猫”神经元的权重：它对所有特征都给了较高的正权重，因为它认为这些特征都和猫有关。
第二行是“狗”神经元的权重：它对“尖耳朵”和“圆眼睛”给了负权重（可能它认为狗的耳朵和眼睛是另一种形状）。
第三行是“其他”神经元的权重。

2. 偏置 (Biases)

每个神经元还有一个独立的偏置项。你可以把它理解为一个“基础分”或者“激活阈值”，它不受任何输入的影响。我们有3个神经元，所以有3个偏置值：

Biases=

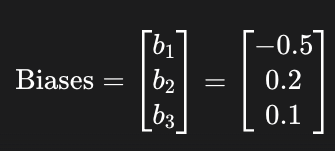
添加图片注释，不超过 140 字（可选）

计算过程

现在我们来计算每个神经元的输出分数。计算方法是：将输入向量与该神经元的权重向量做点积，然后加上偏置。

神经元1 (“猫”的分数):

Score猫=(Inputs⋅Weights猫)+Bias猫

=(2×0.8+1×0.7+3×0.9+5×0.6)+(−0.5)

=(1.6+0.7+2.7+3.0)−0.5

=8.0−0.5=7.5

神经元2 (“狗”的分数):

Score狗=(Inputs⋅Weights狗)+Bias狗

=(2×−0.5+1×0.4+3×−0.8+5×0.2)+(0.2)

=(−1.0+0.4−2.4+1.0)+0.2

=−2.0+0.2=−1.8

神经元3 (“其他”的分数):

Score其他=(Inputs⋅Weights其他)+Bias其他

=(2×0.1+1×−0.2+3×0.3+5×−0.4)+(0.1)

=(0.2−0.2+0.9−2.0)+0.1

=−1.1+0.1=−1.0

最终结果

经过这个全连接层的计算，我们得到的最终输出是一个包含3个分数的向量：[7.5, -1.8, -1.0]。

这个结果很清晰地表明：根据输入的特征和当前层的权重，网络认为这张图片是“猫”的可能性远大于“狗”或“其他”。如果这是最后一层，再经过Softmax函数转换成概率，我们就会得到一个非常接近 [99%, 0.5%, 0.5%]这样的结果。

和卷积层的Filter一样，这里的权重 (Weights) 和偏置 (Biases) 也是网络通过反向传播和梯度下降，在大量数据上训练学习到的。

总结一下完整的CNN流程：

[输入图片] -> [特征提取部分 (卷积层 + 池化层)] -> [压平] -> [分类决策部分 (全连接层)] -> [输出概率]

Pytorch 代码实现

接下来，我们用pytorch实现一个mnist手写字识别，来展示CNN的具体使用方式

import torch
import torch.nn as nn
import torch.optim as optim
from torchvision import datasets, transforms
from torch.utils.data import Dataloader# -----------------------------------
# 步骤 1: 定义CNN模型结构
# -----------------------------------
class SimpleCNN(nn.Module):def __init__(self):super(SimpleCNN, self).__init__():# 我们的模型将包含两个“卷积 + 池化”块，然后是一个全连接层# 第一个卷积块# 输入: 1个颜色通道 (灰度图), 输出: 16个特征图 (使用了16个filter)# 卷积核大小: 3x3, 步长: 1, 填充: 1 (可以让28x28的图片卷积后尺寸不变)self.conv1 = nn.Conv2d(in_channels=1, out_channels=16, kernel_size=3, stride=1, padding=1)self.relu1 = nn.ReLU()# 最大池化层, 窗口: 2x2, 步长: 2 (图片尺寸会减半，28x28 -> 14x14)self.pool1 = nn.MaxPool2d(kernel_size=2, stride=2)# 第二个卷积块# 输入: 16个特征图 (来自上一层), 输出: 32个特征图
self.conv2 = nn.Conv2d(in_channels=16, out_channels=32, kernel_size=3, stride=1, padding=1)self.relu2 = nn.ReLU()self.pool2 = nn.MaxPool2d(kernel_size=2, stride=2) # 图片尺寸再次减半, 14x14 -> 7x7# 全连阶层self.fc = nn.Linear(32*7*7, 10)def forward(self,x):# 定义数据在网络中的流动顺序# 输入 x 的尺寸: [batch_size, 1, 28, 28]# 第一个卷积块x = self.pool1(self.relu1(self.conv1(x))) # -> [batch_size, 16, 14, 14]# 第二个卷积块x = self.pool2(self.relu2(self.conv2(x))) # -> [batch_size, 32, 7, 7]# flattenx = x.view(-1, 32*7*7)x = self.fc(x)return x# 准备数据
transform = transform.Compose([transform.ToTensor(),transform.Normalize((0.1307,),(0.3081)) # MNIST数据集的均值和方差
])# 下载并加载测试数据
test_dataset = datasets.MNIST(root='./data', train=False, download=True, transform=transform)
test_loader = DataLoader(test_dataset, batch_size=1000, shuffle=False)# -----------------------------------
# 步骤 3: 训练模型
# -----------------------------------model = SimpleCNN()# 损失函数和优化器
criteria = nn.CrossEntropyLoss()
optimizer = optim.Adam(model.paramters(), lr=0.001)# 训练5个epochs为例
for epoch in range(5):for i, (images, labels) in enumerate(train_loader):outputs = model(images)loss = criterion(outputs, labels)# backforwardoptimizer.zero_grad() # 清空上一轮的梯度loss.backward()optimizer.step()print("Finish Training")# -----------------------------------
# 步骤 4: 在测试集上评估模型
# -----------------------------------
model.eval() # 将模型设置为评估模式，这会关闭Dropout等训练时特有的层
with torch.no_grad():correct = 0total = 0for images, labels in testloader:outputs = model(images)_, predicted = torch.max(output.data, 1)total += labels.size(0)correct += (predicted == labels).sum().item()accuracy = correct / totalprint(f"accuracy of model is {100*accuracy}%")

上面的代码中的nn.CrossEntropyLoss 是 PyTorch 中用于多分类任务最常用的损失函数。我们可以把它理解为模型的**“考官”或“评分系统”。它的唯一职责就是：拿到模型的预测结果和真实答案，然后给出一个分数（也就是损失值 Loss**），这个分数衡量了模型“错得有多离谱”。