leetcode 974 和可被K整除的子数组

一、题目描述

二、解题思路

整体思路

由于是求连续区间内元素的和，所以可以用前缀和的思想来做，在具体实现中，无需真的预处理出一个前缀和数组，只需要用一个sum来累加，并用哈希表来统计次数即可。本题思路与leetcode560和为K的子数组一致。

具体思路

(1)枚举出所有以i位置为结尾的和可被K整除的子数组，然后更新i，就可以找出所有和可被i整除的子数组。如图所示：

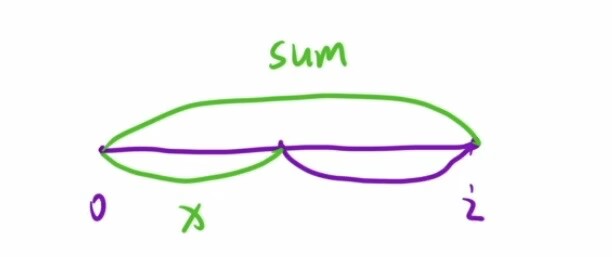
(2)(sum-x)%k=0，由同余定理可得：sum%k=x%k，即要找出[0,i-1]区间内前缀和对k取模等于sum[i]对k取模的子数组的数量。

(3)为了避免哈希表失真，我们需要对取模操作进行修正，因为在C++中负数对正数取模的结果为负数，但是我们需要的模为非负数，所以int r=(sum%k+k)%k;

三、代码实现

时间复杂度：T(n)=O(n)

空间复杂度：S(n)=O(n)

class Solution {
public:int subarraysDivByK(vector<int>& nums, int k) {//前缀和+哈希unordered_map<int,int> hash;//统计前缀和取模k的频次hash[0]=1;int sum=0,ret=0;for(auto x:nums){sum+=x;int r=(sum%k+k)%k;if(hash.count(r)) ret+=hash[r];hash[r]++;}return ret;}
};