当前位置：首页 > news >正文

【C语言练习】青蛙跳台阶

news 2025/8/25 15:49:16

一、题目

一只青蛙一次可以跳1个台阶，也可以跳2个台阶，对于n个台阶，一共有多少种跳法。
在这里插入图片描述

二、分析

假设我们用变量n表示台阶数：
n = 1：1跳法（①跳1阶）

n = 2：2种跳法（①跳1阶，跳1阶；②跳2阶）

n = 3：3种跳法（①跳1阶，跳1阶，跳1阶；②跳1阶，跳2阶；③跳2阶，跳1阶）
n = 4：5种跳法（①跳1阶，跳1阶，跳1阶，跳1阶；②跳1阶，跳1阶，跳2阶；③跳1阶，跳2阶，跳1阶；④跳2阶，跳1阶，跳1阶；⑤跳2阶，跳2阶）
…
从n = 4（或者n = 3）我们可以看出，每一种跳法都能够看成是前面两种跳法的延续（不同颜色对应），可以看成是斐波那契数列。
我们假设f(n)表示的是n阶台阶跳法，那么f(n) = f(n-1)+f(n-2)。
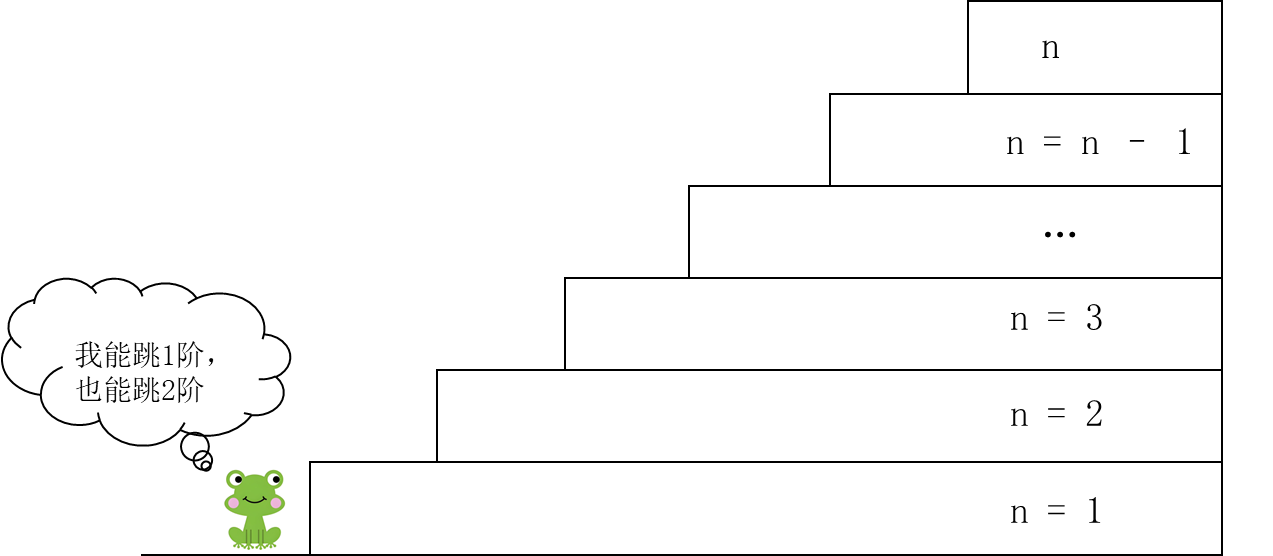
也可以用下图进行解析：
在这里插入图片描述
当青蛙第一次只跳1个台阶，那么还剩下n-1个台阶，就有f(n-1)种跳法。

同理，如果刚开始跳2个台阶，那么剩下台阶的跳法就是f(n-2)。f(n-1)+f(n-2)即是n阶台阶的跳法。

三、代码实现

#include <stdio.h>int Jump(int n)
{if(n <= 2)return n;elsereturn Jump(n - 1) + Jump(n - 2);
}int main()
{int n = 0;scanf("%d", &n);int ret = Jump(n);printf("%d\n", ret);return 0;
}