当前位置： 首页 > news >正文

数据结构 之 【AVL树的简介与部分实现】（部分实现只涉及AVL树的插入问题，包括单旋((右单旋、左单旋))、双旋(左右单旋、右左单旋)等操作）

news 2025/8/24 12:40:39

目录

1.AVL树的概念

2.AVL树节点定义

3.AVL树的插入

1. 按照二叉搜索树的方式插入新节点

2. 调整节点的平衡因子及旋转

(1)更新平衡因子

(2)右单旋

(2)左单旋

(2)左右单旋

(2)右左单旋

3.快速记忆方法

3.调试技巧

1.AVL树的概念

一棵AVL树或者是空树，或者是具有以下性质的二叉搜索树：

(1)左右子树高度之差(简称平衡因子)的绝对值不超过1(-1/0/1)

(2)它的左右子树都是AVL树

显然，AVL树也是递归定义的

下面以K模型实现插入，K模型、KV模型参考我的博客 二叉搜索树的应用

2.AVL树节点定义

//模板，以适应不同数据类型
template<class K>
struct AVLTreeNode//struct定义，将节点暴露方便后续使用
{//三叉链AVLTreeNode<K>* _left;AVLTreeNode<K>* _right;AVLTreeNode<K>* _parent;//键值与平衡因子K _key;int _bf;//new一个新节点时需要调用节点的构造函数AVLTreeNode(const K& key):_left(nullptr),_right(nullptr),_parent(nullptr),_key(key),_bf(0){ }//其余默认构造使用编译器自动生成的即可，这里暂且不用手写，也用不到
};

这个类负责树节点的定义及初始化：

(1)使用模板，以适应不同数据类型

(2)struct定义，将节点暴露方便后续使用

(3这里使用三叉链，即一个节点既保存其左右孩子节点指针又保存其父亲节点指针

3.AVL树的插入

AVL树是特殊的二叉搜索树，AVL树的插入就是在二叉搜索树插入的基础上通过更新平衡因子，进而按需旋转，最终达到左右子树高度差的绝对值不超过1的过程

那么AVL树的插入过程可以分为两步：

1. 按照二叉搜索树的方式插入新节点

template<class K>
class AVLTree
{typedef AVLTreeNode<K> Node;
public://这里只讲AVL树的插入问题，重在了解它的性质特点bool Insert(const K& key){//先查找，再插入(需要考虑树为空的情况)if (!_root){_root = new Node(key);return true;}//树不为空Node* cur = _root;Node* parent = _root;while (cur){if (key > cur->_key){parent = cur;cur = cur->_right;}else if (key < cur->_key){parent = cur;cur = cur->_left;}else//相同值不能插入，去重效果{return false;}}//找到插入位置了，但是需要链接其父亲节点//父亲节点一定不为空cur = new Node(key);if (key > parent->_key){parent->_right = cur;}else{parent->_left = cur;}cur->_parent = parent;//更新平衡因子//插入结束即是成功return true;
}
private://可以偷懒在这初始化Node* _root = nullptr;
};

前半截插入过程与二叉搜索树一致：
向左向右走，遇到空就开始插入，遇到相同值的就返回false(去重效果)

三叉链！！注意链接父亲节点

2. 调整节点的平衡因子及旋转

平衡因子不是必须的，也可以直接通过高度函数来算，只不过比较麻烦

这里定义 平衡因子 = 右子树高度 - 左子树高度

当然也可以反过来

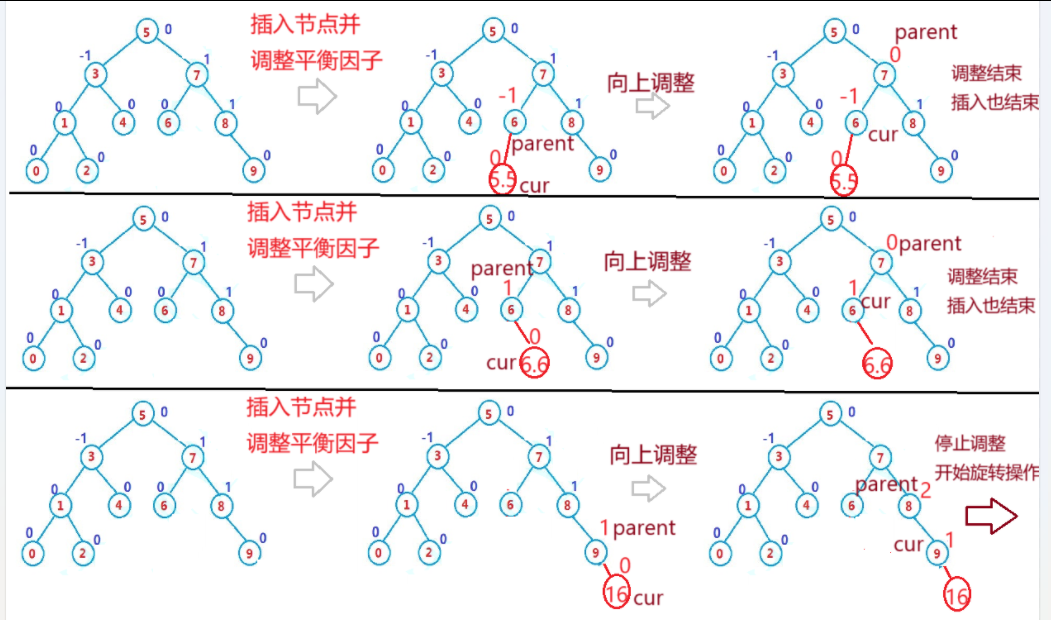
如上图：

(1)插入节点的平衡因子为 0 （其左右子树为空）

(1)插入节点在左，其父亲节点的平衡因子减减

插入节点在右，其父亲节点的平衡因子加加

(1)调整后，父亲节点的平衡因子为0，说明原来的平衡因子为1或-1，即

以父亲节点为根节点的这颗AVL子树符合定义且高度未发生变化不用向上调整平衡因子

(1)调整后，父亲节点的平衡因子为1或-1，说明原来的平衡因子为0，即

以父亲节点为根节点的这颗AVL子树虽符合定义但高度确实发生了变化，需要继续向上调整

(1)调整后，父亲节点的平衡因子为2或-2，

以父亲节点为根节点的这颗子树已不符合定义，需要原地进行旋转操作使其符合定义(平衡)

(1)更新平衡因子

while (parent)
{if (parent->_left == cur){--parent->_bf;}else{++parent->_bf;}if (parent->_bf == 0)//插入结束,树平衡{break;}else if (parent->_bf == 1 || parent->_bf == -1)//子树的高度变化，祖先的平衡因子需要更新{cur = parent;parent = parent->_parent;}else if (parent->_bf == 2 || parent->_bf == -2)//子树不平衡，开始旋转调整{//分情况讨论........//旋转完成后，子树高度与旋转前一致，高度没有变化，跳出循环break;}else{//平衡因子更新错误assert(false);}
}

(1)最后一个else语句是为了检测平衡因子是否更新错误，这样一来可以便利调试

(2)最坏情况就是更新到根节点的平衡因子后截止

---------------------------------------------------------旋转--------------------------------------------------------------

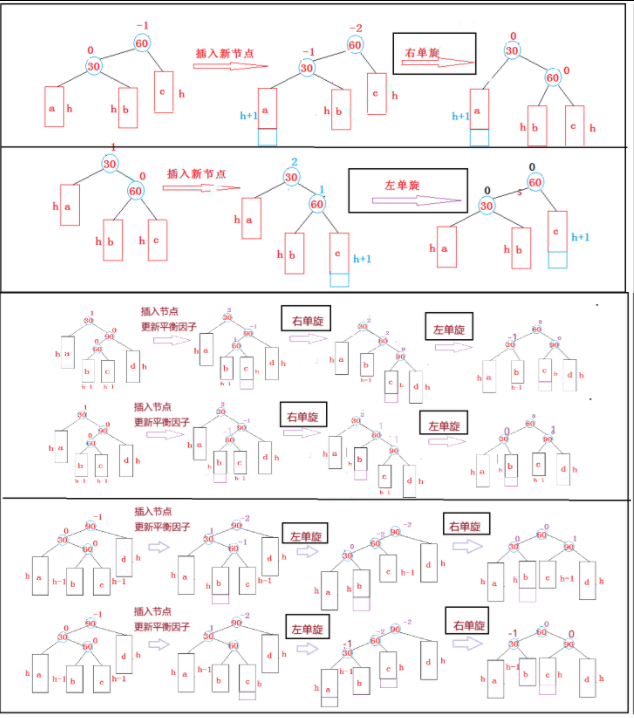
(2)右单旋

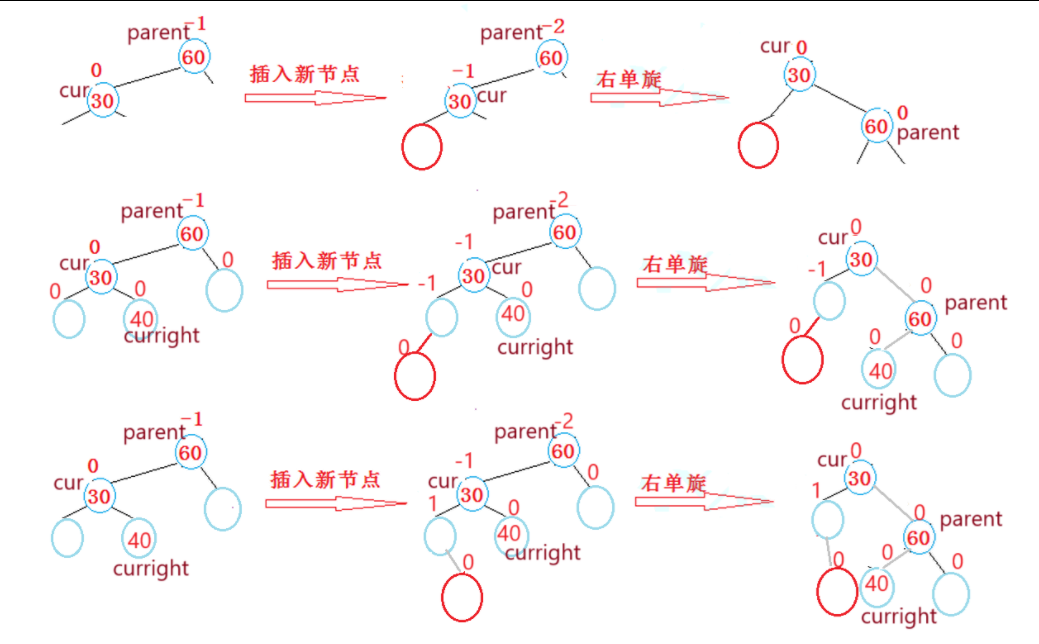
注意三个节点：parent、cur、curright

(1)当 parent->_bf == -2 && cur->_bf == -1 触发右单旋条件

(2)右单旋的实质是把cur的右给到parent的左，parent作为cur的右

可以想象成：parent绕着cur顺时针旋下来

(3)但parent、cur、curright三个节点的平衡因子、父亲节点、左右孩子节点仍要按需更新

(4)旋转之后，三个节点的平衡因子都为0，且该子树的高度与插入前一致

void RotateR(Node* parent)
{Node* cur = parent->_left;Node* curright = cur->_right;//只需更新curright的_parentif (curright)curright->_parent = parent;//更新parent的 _parent,_left，_bfNode* ppnode = parent->_parent;parent->_left = curright;parent->_parent = cur;parent->_bf = 0;//更新cur的 _parent,_right，_bfcur->_bf = 0;cur->_right = parent;if (!ppnode){_root = cur;cur->_parent = nullptr;}else{cur->_parent = ppnode;if (ppnode->_left == parent){ppnode->_left = cur;}else{ppnode->_right = cur;}}
}

(1)curright可能为空

(2)parent的父亲需要指向现在的子树的根节点cur：

提前保存parent的父亲节点(ppnode)，

ppnode为空，说明这是一棵独立的树，此时更新树的根节点及cur的父亲指向

ppnode不为空，说明这是一棵局部的子树，此时更新cur的父亲指向同时让ppnode指向cur

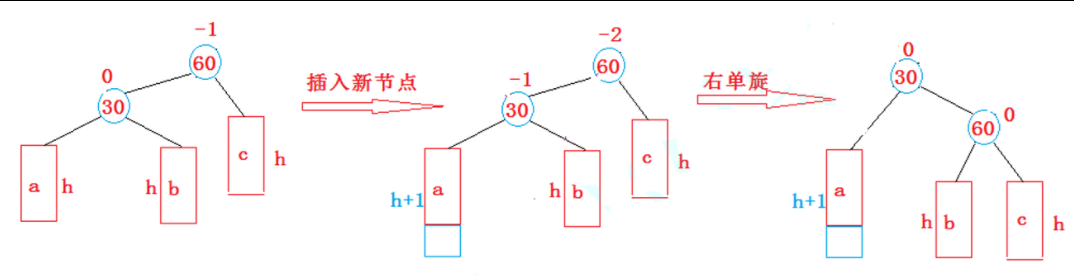
右单旋的场景是数不清的，上图通过抽象得出结论：

当 parent->_bf == -2 && cur->_bf == -1 触发右单旋条件

(2)左单旋

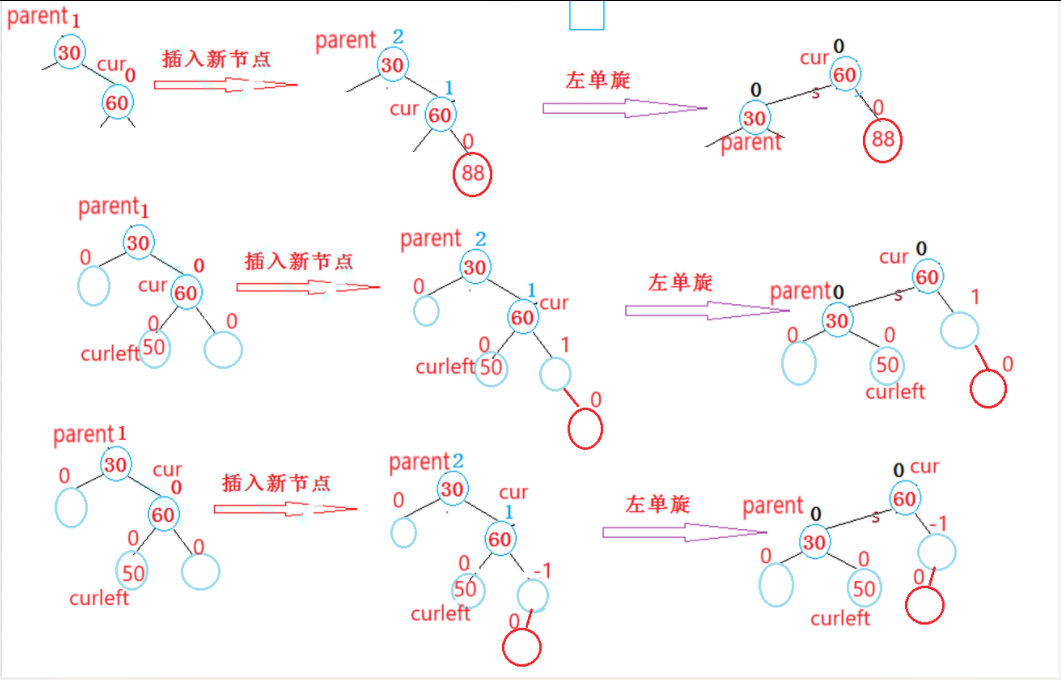
注意三个节点：parent、cur、curleft

(1)当 parent->_bf == 2 && cur->_bf == 1 触发左单旋条件

(2)左单旋的实质是把cur的左给到parent的右，parent作为cur的左

可以想象成：parent绕着cur逆时针旋下来

(3)但parent、cur、curleft三个节点的平衡因子、父亲节点、左右孩子节点仍要按需更新

(4)旋转之后，三个节点的平衡因子都为0，且该子树的高度与插入前一致

void RotateL(Node* parent)
{Node* ppnode = parent->_parent;Node* cur = parent->_right;Node* curleft = cur->_left;//只需更新curleft的_parentif (curleft)curleft->_parent = parent;//更新parent的_right,_parentparent->_right = curleft;parent->_parent = cur;//更新cur 的 _left，_parentcur->_left = parent;if (!ppnode){//一棵独立的树_root = cur;cur->_parent = nullptr;}else{//一棵局部子树if (ppnode->_left == parent){ppnode->_left = cur;}else{ppnode->_right = cur;}cur->_parent = ppnode;}//平衡因子parent->_bf = cur->_bf = 0;
}

(1)curleft 可能为空

(2)parent的父亲需要指向现在的子树的根节点cur：

提前保存parent的父亲节点(ppnode)，

ppnode为空，说明这是一棵独立的树，此时更新树的根节点及cur的父亲指向

ppnode不为空，说明这是一棵局部的子树，此时更新cur的父亲指向同时让ppnode指向cur

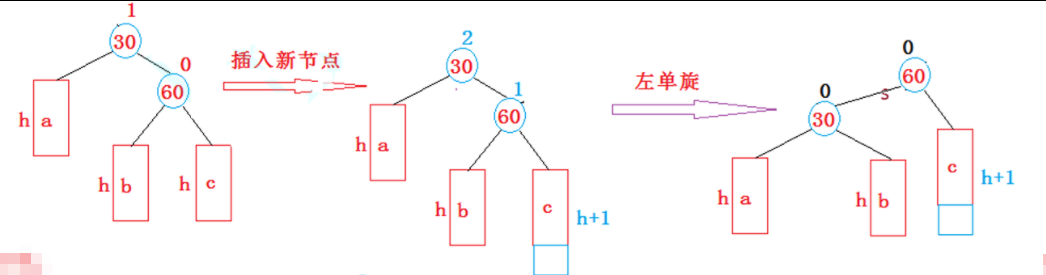
右单旋的场景是数不清的，上图通过抽象得出结论：

当 parent->_bf == 2 && cur->_bf == 1 触发左单旋条件

(2)左右单旋

双旋就是旋转两次的意思

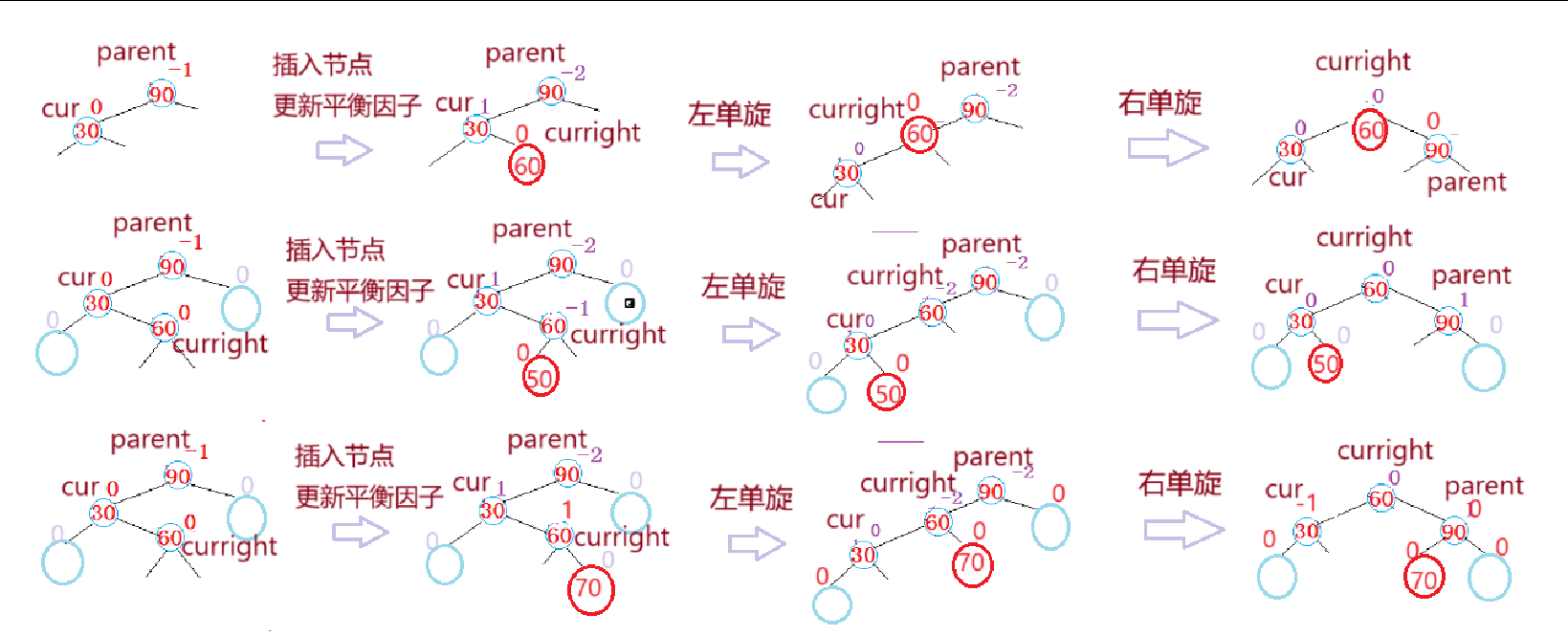
注意三个节点：parent、cur、curright

(1)当 parent->_bf == -2 && cur->_bf == 1 触发左右单旋条件

(2)左右单旋的实质是将curright的左给到cur的右，curright的右给到parent的左

cur成为curright的左，parent成为curright的右，curright成为根节点，即

先左单旋根节点为cur的AVL树，再右单旋根节点为parent的AVL树

(3)旋转之后，该AVL树的高度与插入前一致

插入节点的祖先的平衡因子在插入后已经向上更新，但单旋会将parent、cur、curright的平衡因子都变为0，事实上，curright子树的插入会影响parent、cur的平衡因子

此时双旋的重点变为更新节点的平衡因子

(1)curright为插入节点时，

根据左右单旋的实质，此时三个节点(parent、cur、curright)的平衡因子均为0

(2)插入节点为curright的左孩子节点时，

根据左右单旋的实质，curright、cur的平衡因子为0，parent的平衡因子为1

(3)插入节点为curright的右孩子节点时，

根据左右单旋的实质，curright、parent的平衡因子为0，cur的平衡因子为-1

提前保存curright的平衡因子即可区分上述三种情况

void RotateLR(Node* parent)
{Node* cur = parent->_left;Node* curright = cur->_right;int bf = curright->_bf;RotateL(cur);RotateR(parent);if (bf == 0){curright->_bf = 0;parent->_bf = 0;cur->_bf = 0;}else if (bf == 1){curright->_bf = 0;parent->_bf = 0;cur->_bf = -1;}else if (bf == -1){curright->_bf = 0;parent->_bf = 1;cur->_bf = 0;}else{assert(false);}}

最后一个else语句用来判断平衡因子是否更新错误

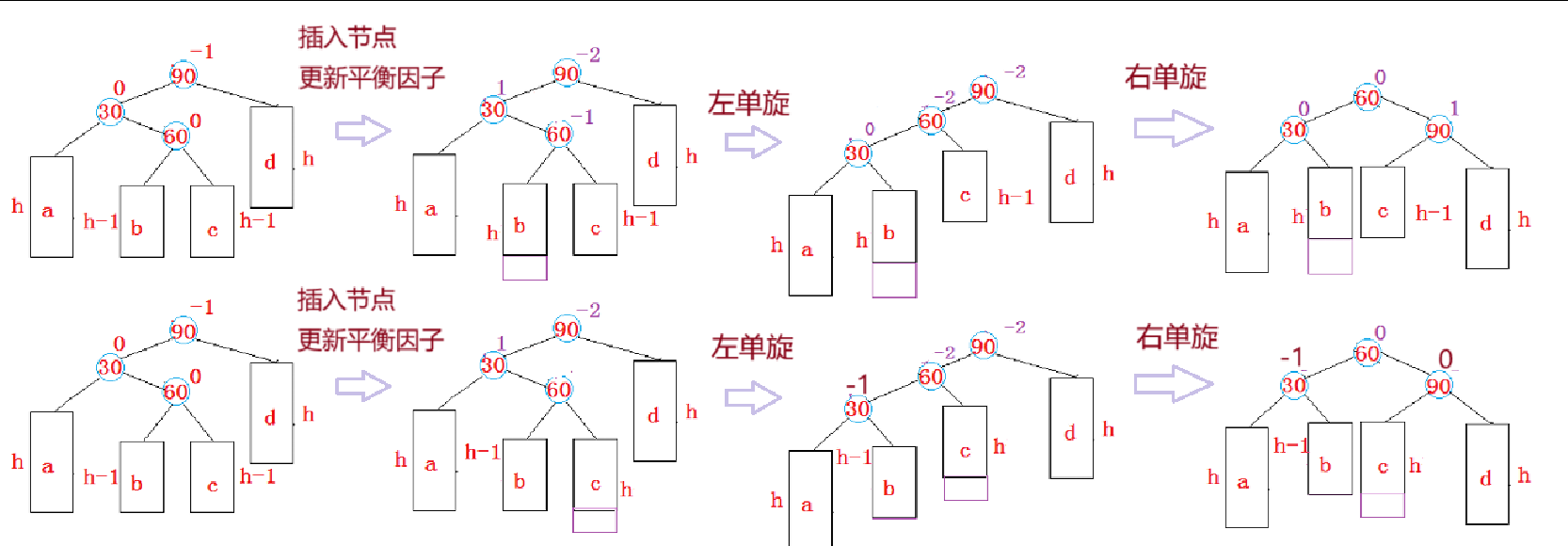
左右单旋的场景是数不清的，上图通过抽象得出结论：

当 parent->_bf == -2 && cur->_bf == 1 触发左右单旋条件

且旋转之后，该AVL树的高度与插入前一致

(2)右左单旋

双旋就是旋转两次的意思

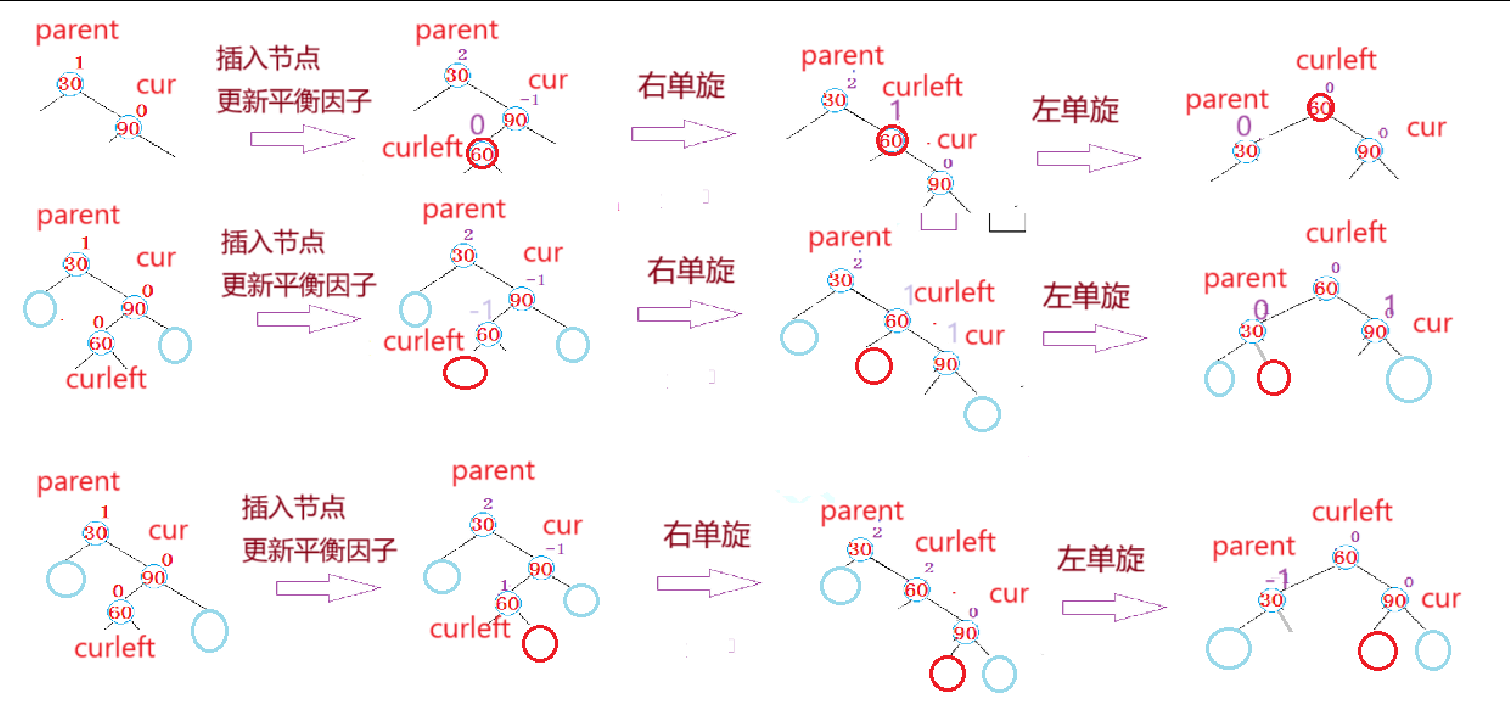
注意三个节点：parent、cur、curleft

(1)当 parent->_bf == 2 && cur->_bf == -1 触发右左单旋条件

(2)右左单旋的实质是将curleft的左给到parent的右，curleft的右给到cur的左

parent成为curleft的左，cur成为curleft的右，curleft成为根节点，即

先右单旋根节点为cur的AVL树，再左单旋根节点为parent的AVL树

(3)旋转之后，该AVL树的高度与插入前一致

插入节点的祖先的平衡因子在插入后已经向上更新，但单旋会将parent、cur、curleft的平衡因子都变为0，事实上，curleft子树的插入会影响parent、cur的平衡因子

此时双旋的重点变为更新节点的平衡因子

(1)curleft为插入节点时，

根据左右单旋的实质，此时三个节点(parent、cur、curleft)的平衡因子均为0

(2)插入节点为curleft的左孩子节点时，

根据左右单旋的实质，curleft、parent的平衡因子为0，cur的平衡因子为1

(3)插入节点为curleft的右孩子节点时，

根据左右单旋的实质，curleft、cur的平衡因子为0，parent的平衡因子为-1

提前保存curleft的平衡因子即可区分上述三种情况

void RotateRL(Node* parent)
{Node* cur = parent->_right;Node* curleft = cur->_left;int bf = curleft->_bf;RotateR(cur);RotateL(parent);//双旋的实质是将curleft的左给到parent的右，curleft的右给到cur的左// curleft成为子树的根节点//双旋重在更新平衡因子if (bf == 0){curleft->_bf = 0;parent->_bf = 0;cur->_bf = 0;}else if (bf == 1){curleft->_bf = 0;parent->_bf = -1;cur->_bf = 0;}else if (bf == -1){curleft->_bf = 0;parent->_bf = 0;cur->_bf = 1;}else{assert(false);}
}

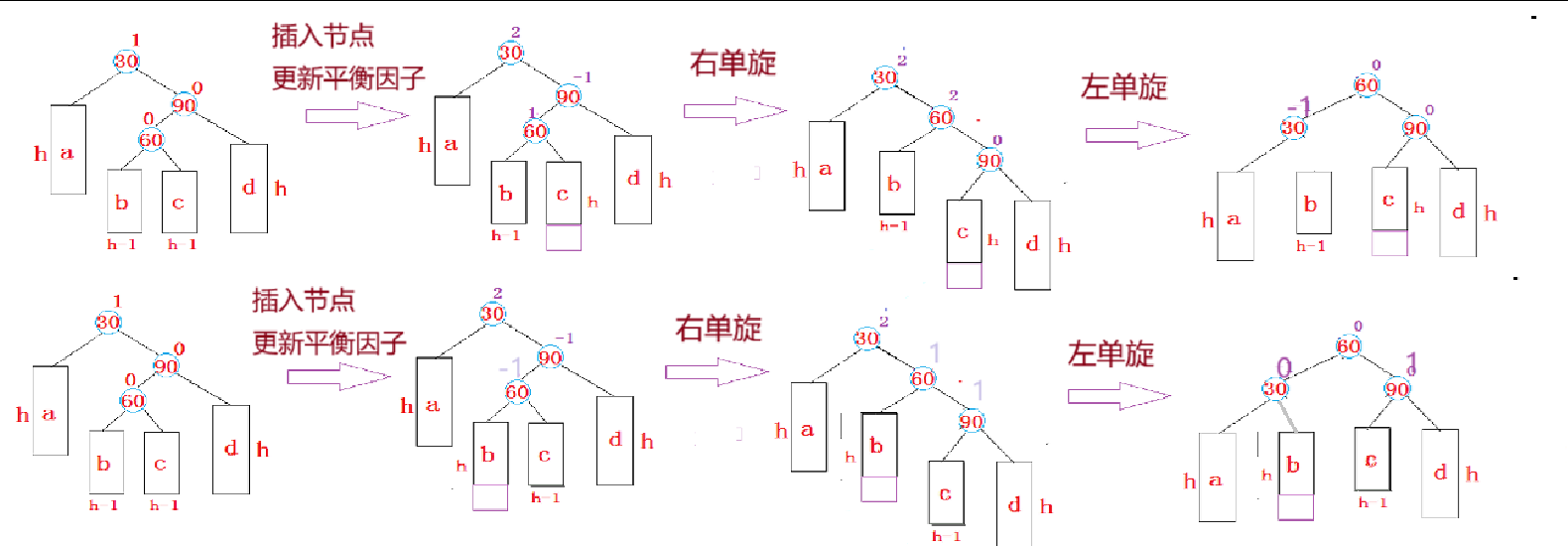
右左单旋的场景是数不清的，上图通过抽象得出结论：

当 parent->_bf == 2 && cur->_bf == -1 触发左右单旋条件

且旋转之后，该AVL树的高度与插入前一致

3.快速记忆方法

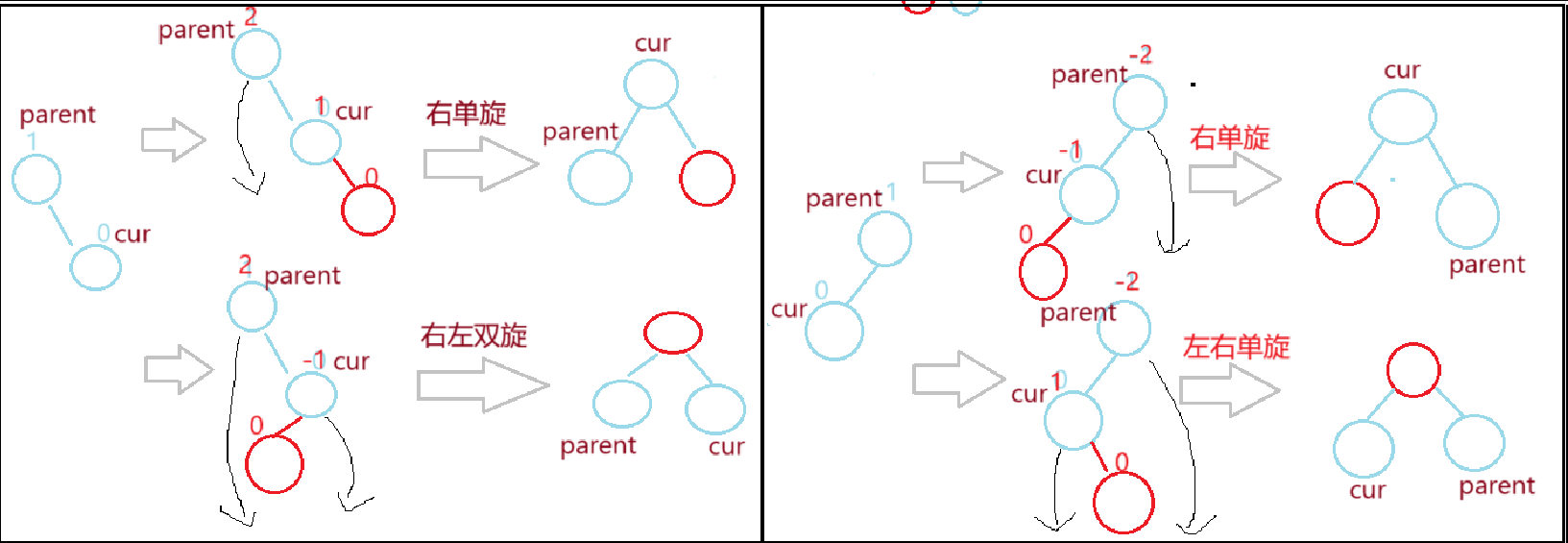
parent与cur的不同链接及cur的左右插入正好对应四种旋转要求

if (parent->_bf == 2 && cur->_bf == 1)
{RotateL(parent);
}
else if (parent->_bf == -2 && cur->_bf == -1)
{RotateR(parent);
}
else if (parent->_bf == -2 && cur->_bf == 1)
{RotateLR(parent);
}
else if (parent->_bf == 2 && cur->_bf == -1)
{RotateRL(parent);
}

3.调试技巧

AVL的插入包括查找、链接、更新平衡因子、旋转等多个步骤，单步调试很困难

这里罗列几个调试技巧

(1)以调试运行

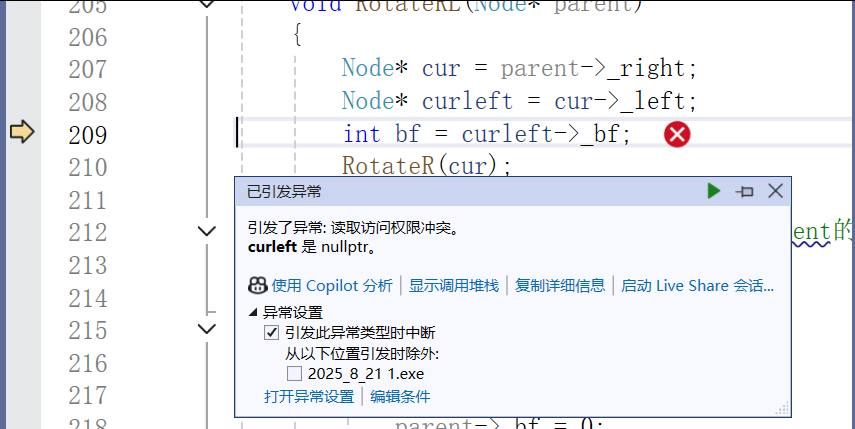
vs2022中，快捷键F5，以调试运行，可使程序在异常抛出时中断

(2)调用堆栈

vs2022中，快捷键 Alt + 7，打开调用堆栈窗口，可初步查出崩溃的节

(3)条件断点

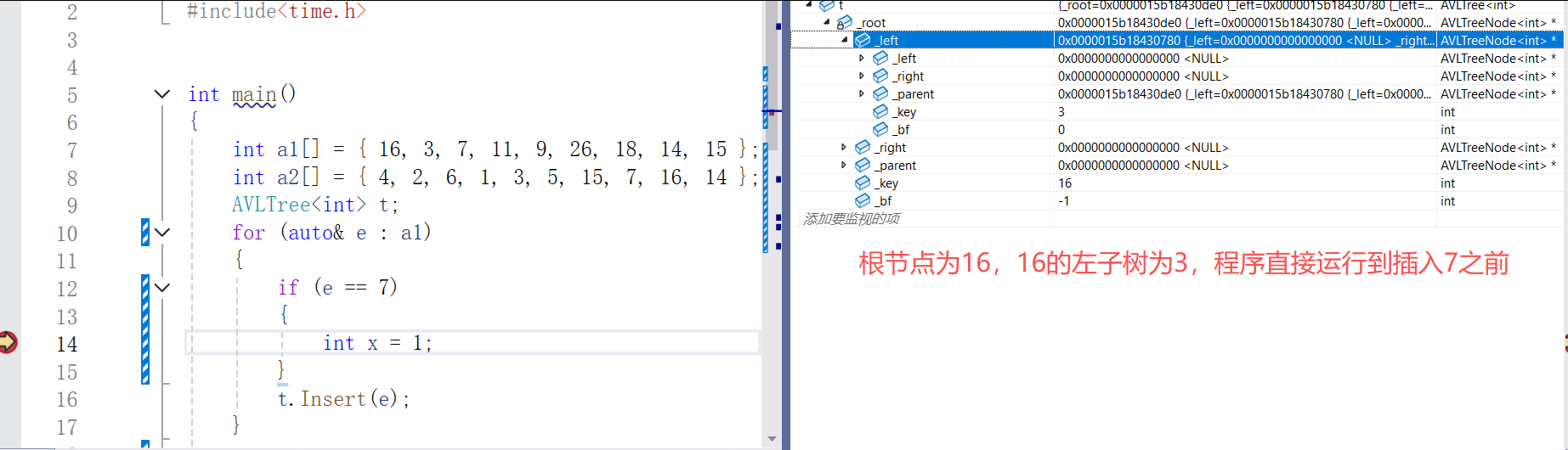
当主观判断可能是在某一节点出错时，写一段无关紧要的代码使程序运行到插入该节点前

(4)借助辅助代码

bool IsBalance()
{return _IsBalance(_root);
}int TreeHeight(Node* root)
{if (!root)return 0;int leftH = TreeHeight(root->_left);int rightH = TreeHeight(root->_right);return leftH > rightH ? leftH + 1 : rightH + 1;
}bool _IsBalance(Node* root)
{if (!root)return true;//后序遍历，计算高度稍微简化了if (!_IsBalance(root->_left))return false;if (!_IsBalance(root->_right))return false;int leftH = TreeHeight(root->_left);int rightH = TreeHeight(root->_right);//先手，平衡因子出错就不玩了if (rightH - leftH != root->_bf){cout << root->_key << "的平衡因子更新错误(实际上->存储的)："<< rightH - leftH << "->" << root->_bf << endl;return false;}//AVL树的特性，高度差小于1if (abs(rightH - leftH) > 1){cout << root->_key << "不平衡" << endl;return false;}return true;
}

中序遍历只能验证该树是否是二叉搜索树，AVL树的验证重点在于左右子树的高度差

该辅助代码可以找到平衡因子更新出错的节点，进而配合前面的条件断点锁定出错的地方

http://www.xdnf.cn/news/1353727.html

相关文章：

  • SAP FI 应收应付账龄分析
  • leetcode26：删除有序数组中的重复项Ⅰ（快慢指针解法）
  • X射线胸部肺炎检测：基于深度学习的医学影像分析项目
  • 概率论基础教程第六章 随机变量的联合分布(二)
  • 告别SaaS数据绑架，拥抱数据主权：XK+独立部署版跨境商城定制，为海外物流企业深度赋能
  • 遥感机器学习入门实战教程｜Sklearn案例⑨：数据预处理（Processing）
  • 不用 if-else，Spring Boot 怎么知道 ?status=10 是哪个枚举？
  • 小白成长之路-k8s原理（一）
  • STM32学习笔记19-FLASH
  • [Mysql数据库] 选择备份策略选择题
  • 工业场景烟雾识别误报率↓82%！陌讯多模态融合算法实战解析
  • 水泉村信息化服务小程序的设计与实验
  • 54 C++ 现代C++编程艺术3-移动构造函数
  • 用 Go + GitHub Models API 打造一个免费的 ChatBot
  • 全面解析JVM预热：原理、价值与实践指南
  • MYSQL-约束
  • 【数据结构】线性表——链表
  • 微服务的编程测评系统15-头像上传-OSS
  • 高阶数据结构---ST表
  • kafaka知识要点
  • VLOOKUP专题训练
  • UE C++ 堆化
  • windows中bat脚本的一些操作（三）
  • 算法第五十五天：图论part05（第十一章）
  • 图论与最短路学习笔记
  • 【数据结构】跳表的概率模型详解与其 C 代码实现
  • 深度学习开篇
  • `strlen` 字符串长度函数
  • python 字典有序性的实现和OrderedDict
  • 计算机网络 各版本TLS握手的详细过程