链表漫游指南:C++ 指针操作的艺术与实践
文章目录
- 0. 前言
- 1. 链表的分类
- 2. 单链表的实现
- 2.1 链表的基本结构——节点(Node)
- 2.2 核心操作详解
- 2.2.1 构造和析构
- 2.2.2 插入操作
- 2.2.3 删除操作
- 2.3.4 其他操作
- 2.4 总结
- 3. 双向链表的实现
- 3.1 基本结构设计
- 3.2 基本操作
- 3.2.1 初始化与销毁
- 3.2.2 插入与删除的核心逻辑
- 3.2.3 常用操作
- 3.3 其他辅助函数
- 3.4 总结
- 4. 与顺序表对比
- 4.1 时间复杂度对比
- 4.2优缺点总结
0. 前言
上一章的顺序表底层是数组,封装了增删查改的功能接口成为了顺序表。存储顺序表的空间是连续的,顺序表非常大时,内存可能无法提供这么大的连续空间,由此,链表就被创造了。在一个复杂的系统中,空闲的内存空间散落在内存各处,而链表通过指针很好的链接起了各个分散的内存空间。
如图:
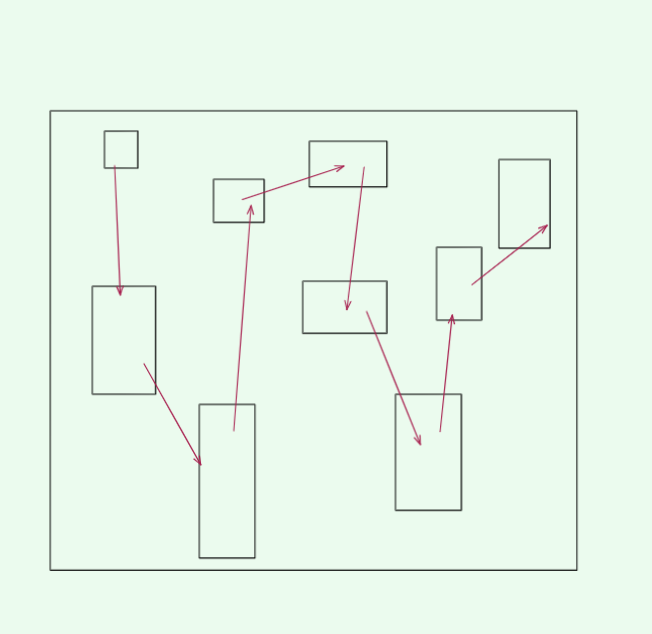
内存空间分配并不连续,但是指针称为维系各个空间的桥梁
链表(linked list) 是一种线性数据结构,每个元素是一个节点对象,各个节点通过指针(或引用)相连接,指针(或引用)记录了下一个节点的内存地址,通过它可以从当前节点访问到下一个节点
1. 链表的分类
链表有多种结构,以下情况组合起来有232^323种:
- 单项或双向
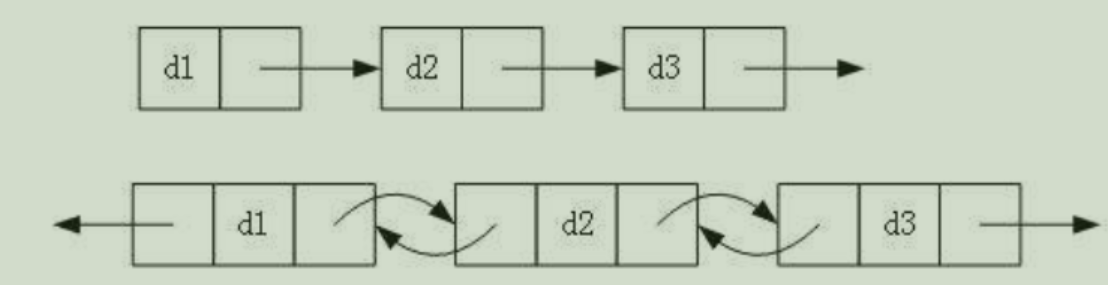
- 带头或不带头
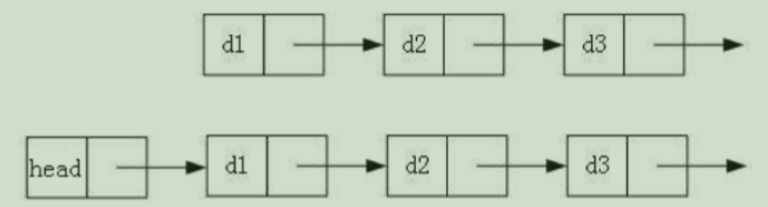
- 循环或不循环
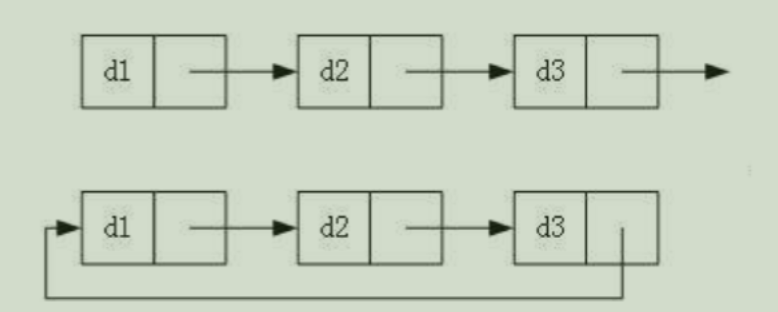
这八种结构种,最常用的是最简单和最复杂的两种结构:
单链表(无头单项不循环链表):结构简单,一般作为其他数据结构的子结构

双向链表(带头双向循环链表):结构最复杂,实际使用中基本都是此结构,操作简单
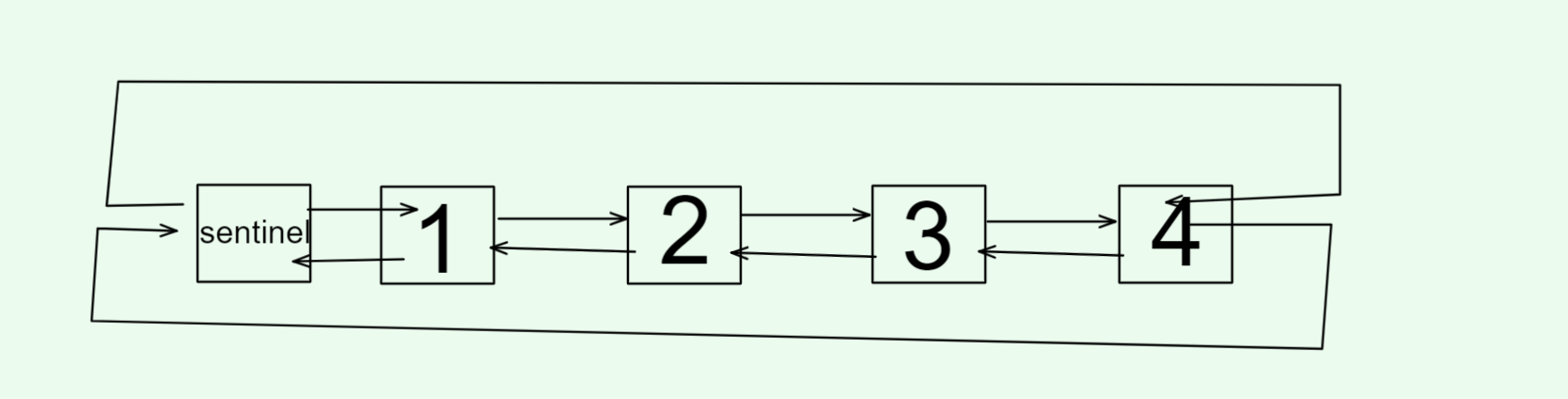
注意:我们把这个带头的头称为哨兵位,哨兵位不存储有效数据(有些时候可能存储链表节点个数),位于链表第一个有效节点(头节点) 的前面。
现在我们来实现一下单链表和双向链表
2. 单链表的实现
2.1 链表的基本结构——节点(Node)
链表的最小单元是节点,C++用结构体或类定义,链表的一个节点包含指针域和数据域,指针域保存该节点指向下一个结点的地址,数据域保存该节点的有效值。还有一个头指针的概念:头指针是链表的门把手,指向链表头节点的指针变量,是链表的入口
// 节点结构体,存储数据和指向下一个结点的指针
struct Node {T _value; // 数据域Node* _next; // 指针域// 节点构造函数 确保新节点创建时_next处于安全状态Node(const T& val) : _value(val), _next(nullptr) {}
};
然后我们将节点放入类中,加入单链表的基本信息:头指针、节点个数
template <typename T>
class single_list{
private:// 节点结构体,存储数据和指向下一个结点的指针struct Node {T _value;Node* _next;// 节点构造函数 确保新节点创建时_next处于安全状态Node(const T& val) : _value(val), _next(nullptr) {}};Node* _head; // 头指针,指向链表的第一个节点size_t _count; // 节点数量
};
我们引入类模板,能使链表的数据类型更多样化,需要什么样的类型我们就可以显式实例化什么类型的链表结构
2.2 核心操作详解
2.2.1 构造和析构
single_list() : _head(nullptr), _count(0) {}
利用初始化列表将链表初始化为空链表,方便后续操作
~single_list() { clear();}
调用清空函数删除所有节点,该函数在下文实现
2.2.2 插入操作
- 头插
// 头插 O(1)
void push_front(const T& val) {// 创建新节点Node* new_node = new Node(val);new_node->_next = _head;_head = new_node;++_count;
}
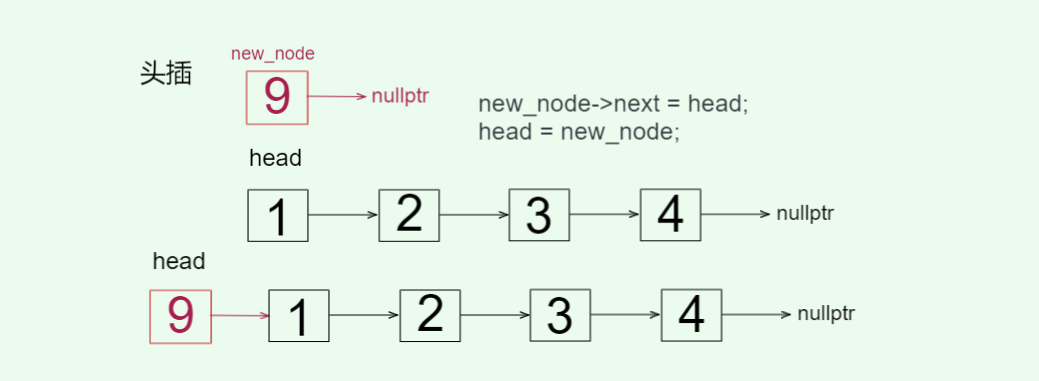
创建新的节点,新节点的指针指向原先的头节点,然后更新头指针的指向
- 尾插
// 尾插 O(n)
void push_back(const T& val) {Node* new_node = new Node(val);// 如果是空链表 new_node就是新的头节点if (!_head) {_head = new_node;}else {// 创建临时变量开始找尾节点Node* cur = _head;while (cur->_next != nullptr) cur = cur->_next;cur->_next = new_node;}++_count;
}
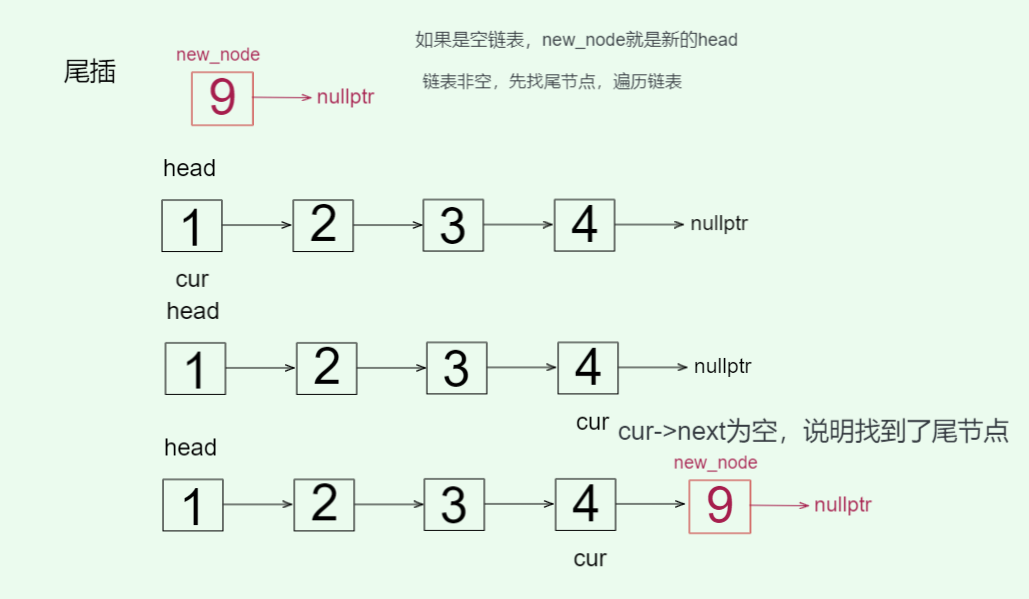
空链表要做单独处理,新节点就是头节点了;链表非空,则要创建临时变量遍历整个链表找尾,一定不能用头指针遍历,使用头指针遍历会丢失头节点的数据
- 指定位置插入节点
// 插入指定位置 O(n)
void insert(int pos, const T& val) {// 确保pos的合法性// pos能取到_count,取到相当于尾插assert(pos >= 0 && pos <= _count);if (pos == 0) return push_front(val);// 创建临时变量找pos位置的节点Node* cur = _head;// 找到pos的前一个节点 cur最终指向pos-1的位置for (size_t i = 0; i < pos - 1; i++)// 循环pos - 1次{cur = cur->_next;}Node* new_node = new Node(val);new_node->_next = cur->_next;cur->_next = new_node;++_count;
}
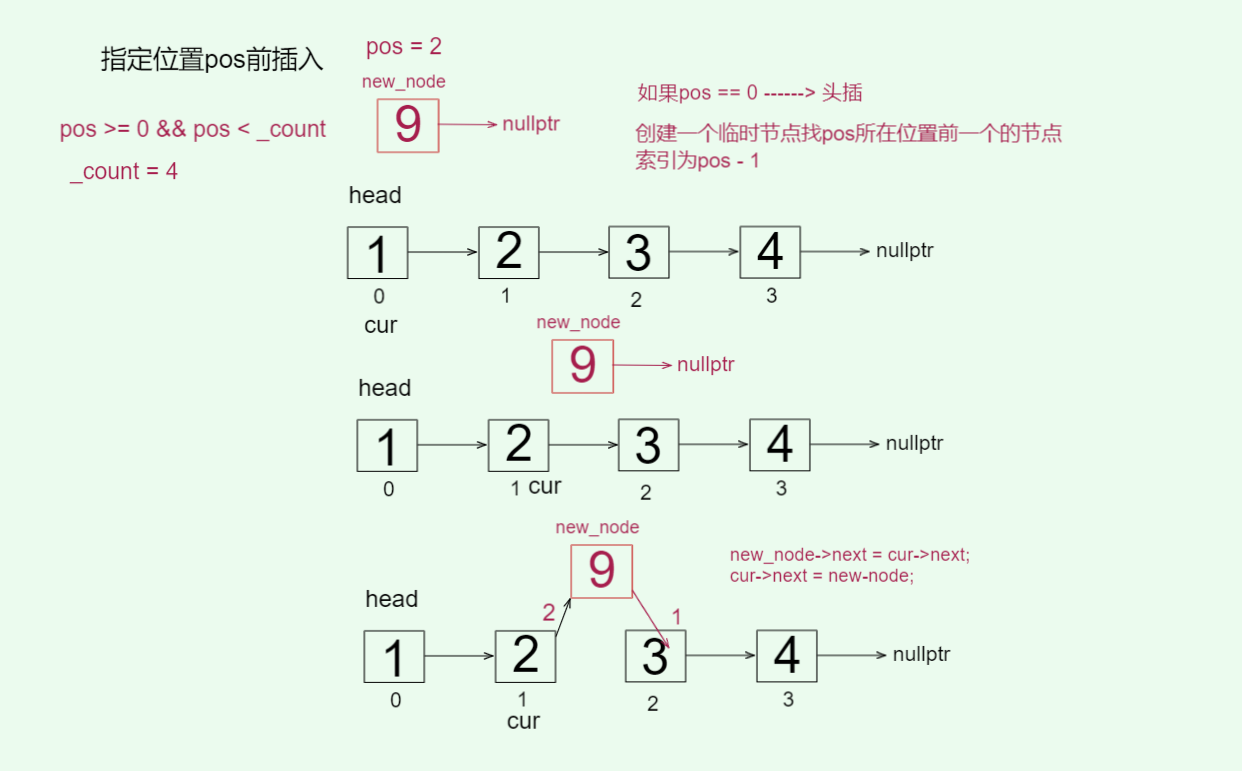
对于用户输入的pos要做检查,pos的值代表索引,从0开始。pos == 0,可以复用头插法,而pos == _count则代表尾插,在下面的循环逻辑中,是找到pos的前一个节点,所以pos的边界判断都可以取到。然后更新指针指向即可
2.2.3 删除操作
空链表不能执行删除操作
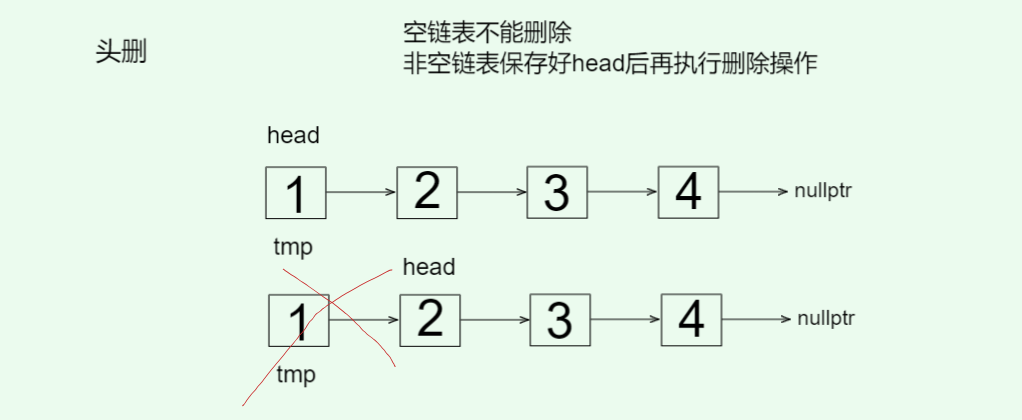
- 头删
// 头删 O(1)
void pop_front() {// 空链表不能删除assert(_head);// 非空链表Node* tmp = _head;_head = tmp->_next;delete tmp;--_count;
}
- 尾删
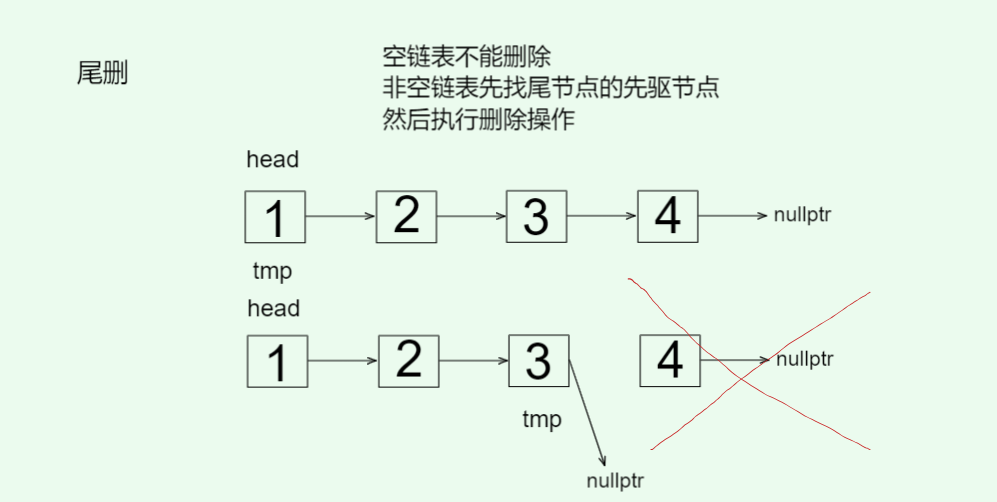
// 尾删 0(n)
void pop_back() {// 空链表不能删除assert(_head);// 非空链表 先找尾节点的先驱节点// 如果只有一个节点 删除即可if (_head->_next == nullptr) {delete _head;_head = nullptr;}else {Node* cur = _head;while (cur->_next->_next) cur = cur->_next;delete cur->_next;cur->_next = nullptr;}--_count;
}
- 删除指定位置节点
// 删除指定位置
void erase(int pos) { // 确保pos合法性assert(pos >= 0 && pos < _count); // pos == 0 头删if (pos == 0) {pop_front();return;}Node* cur = _head;for (size_t i = 0; i < pos - 1; i++) {cur = cur->_next;}Node* tmp = cur->_next; // 保存要删除的节点cur->_next = cur->_next->_next;delete tmp; --_count;
}

2.3.4 其他操作
size_t size() {return _count;
}bool empty() {return _count == 0;
}void clear() {while (_head) {Node* tmp = _head;_head = _head->_next;delete tmp;}_count = 0;
}void Print()
{if (!_head) { // 空链表处理std::cout << "nullptr" << std::endl;return;}Node* cur = _head;while (cur) { // 遍历所有节点std::cout << cur->_value; if (cur->_next) {std::cout << "->";}cur = cur->_next;}std::cout << "->nullptr" << std::endl;
}
2.4 总结
| 操作 | 实现逻辑 | 时间复杂度 |
|---|---|---|
| 头插(push_front) | 新节点指向原头节点,更新头指针 | O(1)O(1)O(1) |
| 尾插(push_back) | 遍历至尾节点,将其指针指向新节点 | O(n)O(n)O(n) |
指定位置pos前插入(insert) | 找到目标位置前一个节点,插入新节点 | O(n)O(n)O(n) |
| 头删(pop_front) | 保存原头节点,头指针后移,释放原节点 | O(1)O(1)O(1) |
| 尾删(pop_back) | 遍历至尾节点前一个节点,释放尾节点 | O(n)O(n)O(n) |
| 指定位置删除(erase) | 找到目标位置前一个节点,释放目标节点 | O(n)O(n)O(n) |
| 清空(clear) | 从头部开始,逐个释放所有节点 | O(n)O(n)O(n) |
- 优点:
- 动态内存分配: 无需预先指定大小,按需分配内存
- 头部操作高效: 头删头插都是O(1)O(1)O(1)
- 插入删除灵活: 不用像顺序表一样挪动大量数据,只需要修改指针
- 缺点:
- 不支持随机访问: 访问第n个元素需要从头遍历
- 尾部操作效率低: 尾插尾删需要遍历到尾部
- 指针管理复杂: 容易出现野指针、空指针问题
- 额外内存开销: 每个节点需要额外空间存储指针
- 使用场景
- 需要频繁进行头部插入删除操作
- 数量不确定,需要动态调整大小
- 内存有限,不适合顺序表使用的场景
- 不需要随机访问元素
3. 双向链表的实现
3.1 基本结构设计
双向链表是带头双向循环链表的简称,结合了三种思路:
- **双向:**每个节点有前驱指针
_prev和后继指针_next,方便前后遍历 - **循环:**链表尾节点
_next指回哨兵位,哨兵位的_prev指向尾节点,整个链表形成一个环 - **带头(带哨兵位):**用一个特殊节点
_sentinel作为表头,不存储有效数据,只起到占位、边界作用
这样做的优点是:
- 统一了插入和删除的逻辑,不用判别头和尾
- 空链表和非空链表的处理方式一致,封装性更好
- 代码更简洁,出错率低
我们先设计一个内部节点结构Node:
template <typename T>
struct Node {T _value;Node* _prev;Node* _next;Node(const T& val) : _value(val),_prev(nullptr),_next(nullptr){}
};
再设计链表类:double_list:
_sentinel:哨兵节点,始终存在。_count:链表中有效节点的个数。
class double_list {
private:struct Node {T _value;Node* _prev;Node* _next;Node(const T& val) : _value(val),_prev(nullptr),_next(nullptr){}};Node* _sentinel; // 哨兵位size_t _count;
};
3.2 基本操作
3.2.1 初始化与销毁
double_list() : _count(0) {// 初始化哨兵位 _prev _next都指向自己_sentinel = new Node(T()); //不存储有效数据_sentinel->_next = _sentinel;_sentinel->_prev = _sentinel;
}~double_list() { clear(); delete _sentinel; }
3.2.2 插入与删除的核心逻辑
1. 在指定位置前插入
// 在pos节点前插入new_node
void insert_node(Node* pos, Node* new_node) {// 先确定好new_node的位置new_node->_prev = pos->_prev;new_node->_next = pos;// 这里顺序不能反了pos->_prev->_next = new_node;pos->_prev = new_node;++_count;
}
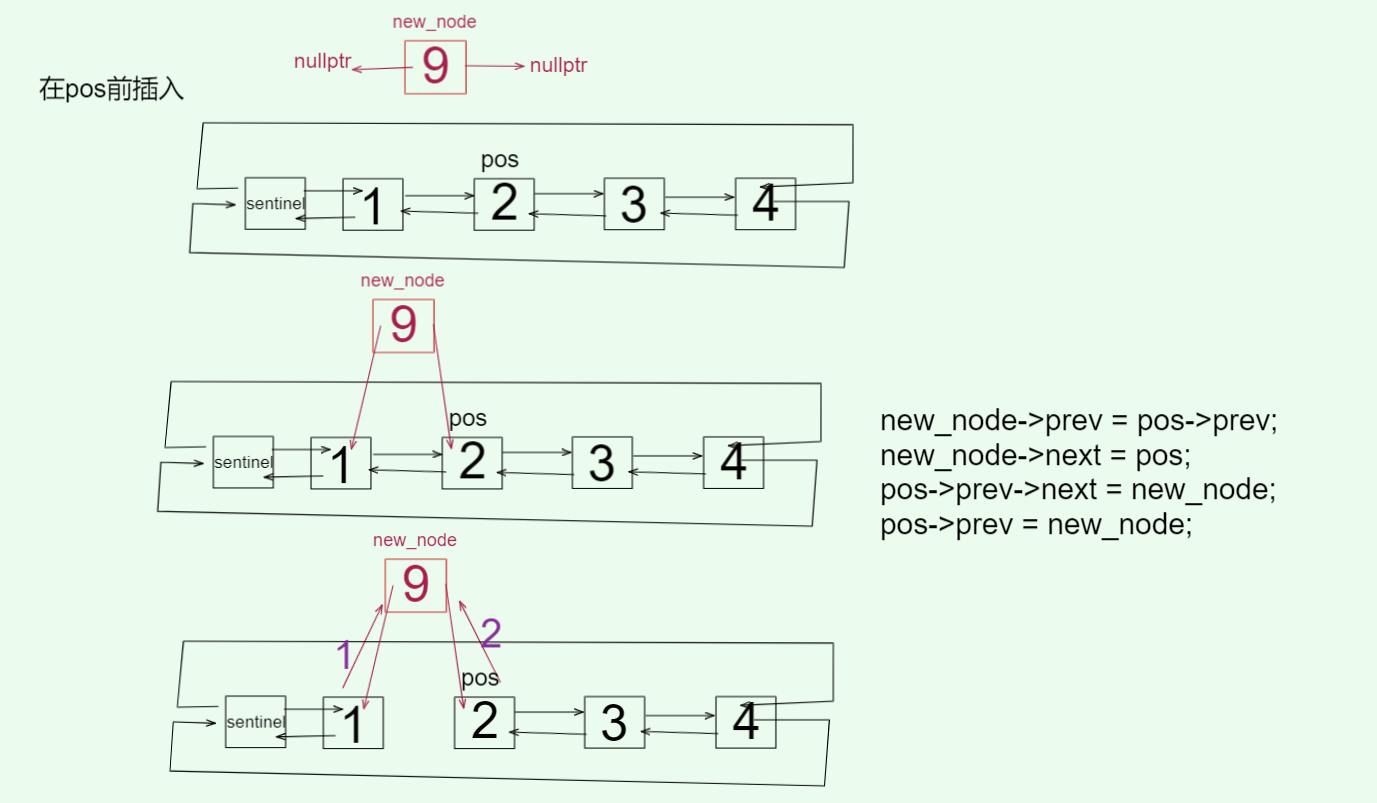
处理指针指向顺序不能颠倒,要先考虑原有节点存在,这里详细讲一下,后续不再赘述。
对任意相邻三点 A <-> B <-> C:
A->_next == BB->_prev == AB->_next == CC->_prev == B
做插入/删除时,不要提前破坏老的不变量,要么先把新节点“准备好”,要么先把“邻居接好”,保证任何时刻都能从 S 沿 _next 或 _prev 找回环,不会丢失链。所以,在 pos 前插入 new_node 的正确顺序为:设:B = pos A = B->_prev
安全顺序(推荐):
-
先给新节点“自报家门”(只写新节点,不动旧链)
new_node->_prev = A; new_node->_next = B; -
再接左边的
_nextA->_next = new_node; -
最后接右边的
_prevB->_prev = new_node;
这套顺序的逻辑是:
- 第1步只动
new_node,不破坏原有结构; - 第2步把
A指向新节点,此时从左侧走到new_node没问题; - 第3步把
B的前驱改为新节点,完成闭合; - 全程不会出现“链断掉一截找不回来的窗口期”。
为什么不能颠倒?一个典型反例:
// ❌ 先改 B->_prev,再去用 pos->_prev
B->_prev = new_node;
B->_prev->_next = new_node; // 此时 B->_prev 已是 new_node,这行等价 new_node->_next = new_node,链炸
如果没有缓存 A(而是反复写 pos->_prev),一旦你先把 B->_prev 改成了 new_node,再通过 pos->_prev 想找到老的 A 就晚了——你拿到的是 new_node,从而把 new_node->_next 错误地指向 new_node 自己,造成环路破坏。
结论:如果你不缓存
A,就必须按先写 new_node 的 _prev/_next,再写 A->_next,最后写 B->_prev的顺序。
如果你缓存了:Node* A = B->_prev;,则可以适当调换 2、3 两步的先后(先改B->_prev或先改A->_next都行),因为A已经固定,不会丢。
2. 删除指定节点
// 删除指定节点
void erase_node(Node* pos) {pos->_prev->_next = pos->_next;pos->_next->_prev = pos->_prev;delete pos;--_count;
}
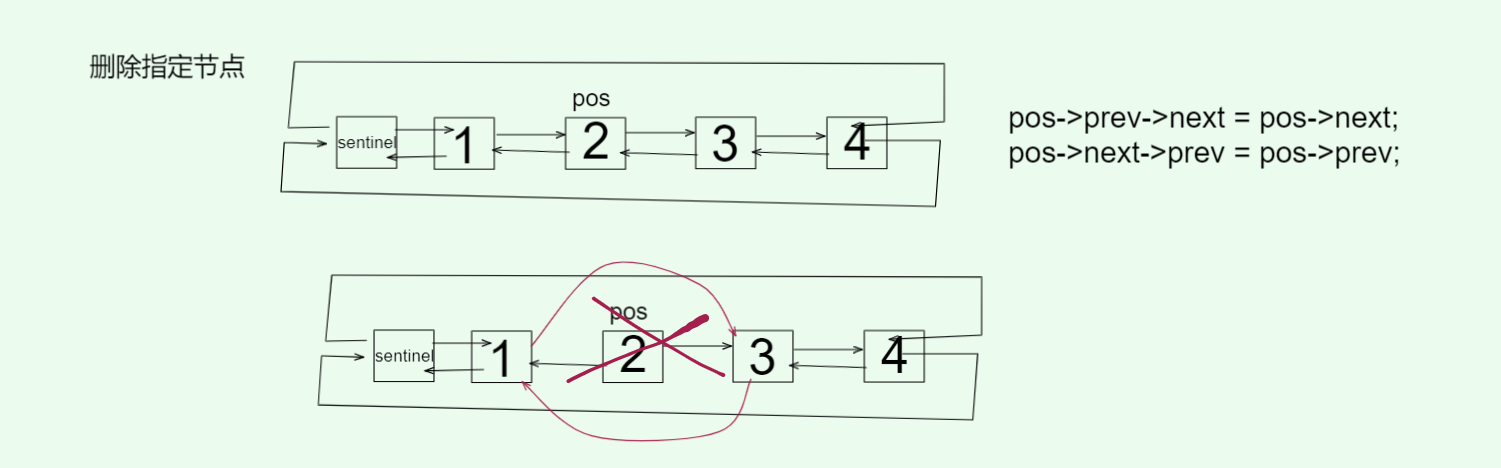
还是用这条链路举例子:A <-> B <-> C
设:B = pos A = B->_prev C = B->_next
安全顺序(必须这样):
-
先把邻居接好,绕过
BA->_next = C; C->_prev = A; -
再释放
Bdelete B;
为什么?
- 如果你先
delete B,随后再去访问B->_prev或B->_next来接回邻居,就会解引用野指针,是未定义行为。 - 先把
A和C直接连起来,保证环不断;最后才安全释放B。
常见错误:
delete B; // ❌ 提前释放
A->_next = B->_next; // 立刻野指针解引用
有了这两个基础操作,头插、尾插、头删、尾删都能用它们实现。所以这两个操作可以封装到private中,仅供类自己使用。
3.2.3 常用操作
1. 头插&尾插
// 头插 在哨兵位后插入
void push_front(const T& val) {insert_node(_sentinel->_next, new Node(val));
}// 尾插 在哨兵位前插入
void push_back(const T& val) {insert_node(_sentinel, new Node(val));
}
2. 头删&尾删
// 头删 哨兵位的next
void pop_front() {if(empty()) throw std::out_of_range("List empty");erase_node(_sentinel->_next);
}// 尾删 哨兵位的prev
void pop_back() {if (empty()) throw std::out_of_range("List empty");erase_node(_sentinel->_prev);
}
3. 访问指定位置
// 访问指定位置节点 用索引
T& at(int pos) {if(pos < 0 || pos >= _count) throw std::out_of_range("Index out of range");//创建临时节点访问链表// 哨兵位的next索引是0Node* cur = _sentinel->_next;for (size_t i = 0; i < pos; i++){cur = cur->_next;}return cur->_value;}4. 指定位置插入&删除
// 在pos位置节点前插入新节点
void insert(int pos, const T& val) {if(pos < 0 || pos > _count) throw std::out_of_range("Insert position out of range");// 要在pos前插入 就从哨兵位走Node* cur = _sentinel;for (size_t i = 0; i < pos; i++){cur = cur->_next;}insert_node(cur, new Node(val));}// 删除pos位置的节点
void erase(int pos) {if(pos < 0 || pos >= _count) throw std::out_of_range("Erase position out of range");// 找pos位置 从索引为零的位置开始Node* cur = _sentinel->_next;for (size_t i = 0; i < pos; i++){cur = cur->_next;}erase_node(cur);
}
3.3 其他辅助函数
打印链表
void Print() {std::cout << "_sentinel->";Node* cur = _sentinel->_next;while (cur != _sentinel) {std::cout << cur->_value << "->";cur = cur->_next;}std::cout << "_sentinel" << std::endl;
}
清空链表
// 清空链表 保留哨兵位
void clear() {Node* cur = _sentinel->_next;while (cur != _sentinel) {Node* tmp = cur;cur = cur->_next;delete tmp;}_sentinel->_next = _sentinel;_sentinel->_prev = _sentinel;_count = 0;
}
判断链表是否为空
bool empty() const { return _count == 0; }
返回链表长度
size_t size() const { return _count; }
3.4 总结
| 操作 | 说明 | 时间复杂度 |
|---|---|---|
| push_front(val) | 头插,在哨兵后插入新节点 | O(1)O(1)O(1) |
| push_back(val) | 尾插,在哨兵前插入新节点 | O(1)O(1)O(1) |
| insert(pos, val) | 在第 pos 个位置前插入新节点(需遍历到 pos) | O(n)O(n)O(n) |
| insert_node | 已知节点 pos 前插入 new_node,只改指针 | O(1)O(1)O(1) |
| pop_front() | 头删,删除第一个节点 | O(1)O(1)O(1) |
| pop_back() | 尾删,删除最后一个节点 | O(1)O(1)O(1) |
| erase(pos) | 删除第 pos 个节点(需遍历到 pos) | O(n)O(n)O(n) |
| erase_node | 删除已知节点指针 | O(1)O(1)O(1) |
| at(pos) | 按索引访问第 pos 个节点 | O(n)O(n)O(n) |
- 优点
- 带哨兵节点:
_sentinel作为头尾的“标志”,统一了边界条件,避免空链表、头删、尾删的特殊情况。 - 循环结构: 遍历时不用判断
nullptr,走到_sentinel就说明一圈结束。 - 双向链表: 已知某个节点指针时,删除/插入只需改前后两个指针,操作 O(1)O(1)O(1)。
- 动态存储: 不需要连续内存,比数组更灵活。
- 缺点
- 访问效率低:
at、insert、erase都需要顺序遍历, O(n)O(n)O(n)。 - 额外空间开销大 每个节点需要两个指针
_prev和_next,比单链表开销更高。 - 实现复杂: 插入/删除时要维护两个方向的指针,顺序稍有不慎就会出现 bug(比如断链、死循环)。
4. 与顺序表对比
4.1 时间复杂度对比
| 操作 | 数组 (顺序表) | 单向链表 | 双向循环链表(带头) |
|---|---|---|---|
| 按下标访问 | O(1)O(1)O(1) | O(n)O(n)O(n) | O(n)O(n)O(n) |
| 按值查找 | O(n)O(n)O(n) | O(n)O(n)O(n) | O(n)O(n)O(n) |
| 头插 | O(n)O(n)O(n)(需要整体移动) | O(1)O(1)O(1) | O(1)O(1)O(1) |
| 尾插问 | O(1)O(1)O(1)(有容量时) | O(1)O(1)O(1) | O(1)O(1)O(1) |
| 中间插入 | O(n)O(n)O(n)(移动元素) | O(n)O(n)O(n)(遍历到位置) | O(n)O(n)O(n)(遍历到位置) |
| 头删 | O(n)O(n)O(n)(整体移动) | O(1)O(1)O(1) | O(1)O(1)O(1) |
| 尾删问 | O(1)O(1)O(1) | O(n)O(n)O(n)(需找前驱) | O(1)O(1)O(1) |
| 删除已知节点指针 | O(1)(仅数组下标已知时) | O(n)O(n)O(n)(需找前驱) | O(1)O(1)O(1) |
| 空间使用 | 连续空间,高效 | 每节点额外 1 个指针 | 每节点额外 2 个指针 |
| 遍历 | O(n)O(n)O(n) | O(n)O(n)O(n) | O(n)O(n)O(n) |
4.2优缺点总结
顺序表
- 优点:支持随机访问 O(1)O(1)O(1),内存利用率高,局部性好。
- 缺点:插入/删除开销大(需要整体移动),容量固定或扩容开销高。
- 适用场景:频繁访问、较少插入删除。
单链表
- 优点:插入/删除高效,内存分配灵活。
- 缺点:不能快速找到前驱,删除已知节点需 O(n)O(n)O(n),访问慢。
- 适用场景:需要频繁插入/删除,但多在链表头部操作。
双向链表(带头循环)
- 优点:
- 插入/删除效率高,尤其是头尾操作 O(1)O(1)O(1)。
- 已知节点指针时,删除/插入 O(1)O(1)O(1)。
- 带头哨兵,逻辑统一,不需要处理特殊情况。
- 缺点:
- 空间开销更大,每节点要两个指针。
- 随机访问仍是 O(n)O(n)O(n)。
- 实现复杂,指针操作容易出错。
- 适用场景:需要频繁在任意位置插入/删除的场景
