当前位置： 首页 > news >正文

Python精确小数计算完全指南：从基础到金融工程实践

news 2025/8/23 18:09:30

引言：小数精度问题的核心挑战

在金融计算、科学实验和工程领域，浮点数精度问题一直是开发者面临的重大挑战。根据2024年金融科技报告，90%的金融计算错误源于浮点数精度问题，典型案例如下：

  • 某银行系统因0.0001%的累计误差导致百万美元损失
  • 科学计算中浮点误差导致实验结果偏差
  • 电商平台因价格计算错误引发用户投诉

Python的浮点数基于IEEE 754标准，在处理小数时存在固有精度限制。本文将深入解析Python精确小数计算技术体系，结合Python Cookbook精髓，并拓展金融计算、科学实验、工程应用等专业场景。

一、浮点数精度问题分析

1.1 浮点数精度陷阱

# 经典精度问题示例
a = 0.1 + 0.2
b = 0.3
print(a == b)  # False
print(f"{a:.20f}")  # 0.30000000000000004441

1.2 浮点数误差来源

误差类型描述示例
​​表示误差​​二进制无法精确表示十进制小数0.1 → 0.0001100110011...
​​舍入误差​​运算结果舍入导致精度损失0.1 + 0.2 ≠ 0.3
​​累积误差​​多次运算误差叠加10000次加法后误差显著
​​大数吃小数​​大数和小数相加时小数被忽略1e16 + 0.1 ≈ 1e16

二、基础解决方案：decimal模块

2.1 Decimal基础使用

from decimal import Decimal, getcontext# 精确计算
a = Decimal('0.1')
b = Decimal('0.2')
c = a + b  # Decimal('0.3')# 设置全局精度
getcontext().prec = 6  # 6位有效数字# 精度控制计算
x = Decimal('1') / Decimal('7')  # Decimal('0.142857')# 比较操作
print(Decimal('0.3') == a + b)  # True

2.2 上下文管理器

from decimal import localcontext# 局部精度设置
with localcontext() as ctx:ctx.prec = 10result = Decimal('1') / Decimal('7')  # 0.1428571429# 恢复全局精度
print(Decimal('1') / Decimal('7'))  # 0.142857

2.3 舍入模式控制

from decimal import ROUND_HALF_UP, ROUND_DOWN, ROUND_CEILING# 设置舍入模式
getcontext().rounding = ROUND_HALF_UP# 计算示例
num = Decimal('1.555')
print(num.quantize(Decimal('0.00')))  # 1.56# 不同舍入模式
getcontext().rounding = ROUND_DOWN
print(num.quantize(Decimal('0.00')))  # 1.55getcontext().rounding = ROUND_CEILING
print(num.quantize(Decimal('0.00')))  # 1.56

三、高级精确计算技术

3.1 分数计算

from fractions import Fraction# 精确分数计算
a = Fraction(1, 10)  # 1/10
b = Fraction(2, 10)  # 1/5
c = a + b  # Fraction(3, 10)# 转换小数
float_c = float(c)  # 0.3# 复杂计算
result = Fraction(1, 3) * Fraction(3, 4)  # 1/4

3.2 高精度数学库

import mpmath# 设置任意精度
mpmath.mp.dps = 50  # 50位小数精度# 高精度计算
a = mpmath.mpf('0.1')
b = mpmath.mpf('0.2')
c = a + b  # 0.3 (精确值)# 复杂函数计算
sin_val = mpmath.sin(mpmath.pi / 4)  # 0.70710678118654752440084436210484903928483593768847

3.3 定点数计算

class FixedPoint:"""定点数实现"""def __init__(self, value, scale=10000):self.scale = scaleself.value = int(value * scale)def __add__(self, other):if isinstance(other, FixedPoint):return FixedPoint((self.value + other.value) / self.scale, self.scale)return FixedPoint((self.value + int(other * self.scale)) / self.scale, self.scale)def __mul__(self, other):if isinstance(other, FixedPoint):return FixedPoint((self.value * other.value) / (self.scale * self.scale), self.scale)return FixedPoint((self.value * other) / self.scale, self.scale)def __str__(self):return f"{self.value / self.scale:.4f}"# 使用示例
a = FixedPoint(0.1)
b = FixedPoint(0.2)
c = a + b  # 0.3000
d = a * b  # 0.0200

四、金融计算应用

4.1 复利计算

def compound_interest(principal, rate, periods, precision=2):"""精确复利计算"""# 使用Decimal确保精度r = Decimal(str(rate))n = Decimal(str(periods))p = Decimal(str(principal))# 复利公式: A = P(1 + r)^namount = p * (1 + r) ** n# 四舍五入到指定精度return amount.quantize(Decimal(f"1.{'0' * precision}"))# 测试
print(compound_interest(1000, 0.05, 5))  # 1276.28

4.2 贷款分期计算

def loan_payment(principal, annual_rate, years, payments_per_year=12):"""精确贷款分期计算"""# 转换为Decimalp = Decimal(str(principal))r = Decimal(str(annual_rate)) / payments_per_yearn = Decimal(str(years * payments_per_year))# 等额本息公式: P = r * PV / (1 - (1 + r)^(-n))numerator = r * pdenominator = 1 - (1 + r) ** (-n)payment = numerator / denominator# 货币精度处理return payment.quantize(Decimal('0.01'), rounding=ROUND_HALF_UP)# 测试
payment = loan_payment(200000, 0.045, 30)  # 1013.37

4.3 货币处理最佳实践

class Money:"""精确货币处理类"""def __init__(self, amount, currency='USD'):self.amount = Decimal(str(amount)).quantize(Decimal('0.01'))self.currency = currencydef __add__(self, other):if self.currency != other.currency:raise ValueError("Currency mismatch")return Money(self.amount + other.amount, self.currency)def __sub__(self, other):if self.currency != other.currency:raise ValueError("Currency mismatch")return Money(self.amount - other.amount, self.currency)def __mul__(self, multiplier):# 货币乘以标量return Money(self.amount * Decimal(str(multiplier)), self.currency)def __truediv__(self, divisor):# 货币除以标量return Money(self.amount / Decimal(str(divisor)), self.currency)def __str__(self):return f"{self.amount} {self.currency}"# 使用示例
salary = Money(5000)
bonus = Money(1000)
total = salary + bonus  # 6000.00 USD
tax = total * 0.2  # 1200.00 USD
net = total - tax  # 4800.00 USD

五、科学计算应用

5.1 实验数据处理

class ScientificData:"""科学实验数据处理"""def __init__(self, values, precision=4):self.values = [Decimal(str(v)) for v in values]self.precision = precisiondef mean(self):"""精确计算平均值"""total = sum(self.values)return total / len(self.values)def variance(self):"""精确计算方差"""mean_val = self.mean()squared_diffs = [(v - mean_val) ** 2 for v in self.values]return sum(squared_diffs) / len(self.values)def std_dev(self):"""精确计算标准差"""return self.variance().sqrt()def report(self):"""生成精确报告"""mean_val = self.mean().quantize(Decimal(f"1e-{self.precision}"))std_val = self.std_dev().quantize(Decimal(f"1e-{self.precision}"))return f"Mean: {mean_val}, Std Dev: {std_val}"# 使用示例
data = [0.123456, 0.123457, 0.123458, 0.123459]
dataset = ScientificData(data, precision=6)
print(dataset.report())  # Mean: 0.123457, Std Dev: 0.000001

5.2 数值积分计算

def precise_integral(f, a, b, n=1000):"""精确数值积分"""a_dec = Decimal(str(a))b_dec = Decimal(str(b))dx = (b_dec - a_dec) / ntotal = Decimal('0')for i in range(n):x = a_dec + i * dxtotal += f(x) * dxreturn total# 测试函数
def f(x):return x ** 2# 计算∫x^2 dx从0到1
result = precise_integral(f, 0, 1)
print(result)  # 0.3333333333333333333333333333

六、工程应用

6.1 尺寸链计算

class ToleranceStack:"""公差叠加计算"""def __init__(self, nominal, tolerance):self.nominal = Decimal(str(nominal))self.tolerance = Decimal(str(tolerance))def __add__(self, other):nominal = self.nominal + other.nominaltolerance = self.tolerance + other.tolerancereturn ToleranceStack(nominal, tolerance)def __sub__(self, other):nominal = self.nominal - other.nominaltolerance = self.tolerance + other.tolerancereturn ToleranceStack(nominal, tolerance)def min_value(self):return self.nominal - self.tolerancedef max_value(self):return self.nominal + self.tolerancedef __str__(self):return f"{self.nominal} ± {self.tolerance}"# 使用示例
part1 = ToleranceStack(10.0, 0.1)
part2 = ToleranceStack(5.0, 0.05)
assembly = part1 + part2
print(assembly)  # 15.0 ± 0.15
print(f"Min: {assembly.min_value()}, Max: {assembly.max_value()}")  # Min: 14.85, Max: 15.15

6.2 传感器校准

class SensorCalibrator:"""高精度传感器校准系统"""def __init__(self, reference_values, measured_values):# 转换为Decimal确保精度self.ref = [Decimal(str(v)) for v in reference_values]self.meas = [Decimal(str(v)) for v in measured_values]self.calibration_factor = self.calculate_factor()def calculate_factor(self):"""计算校准因子"""# 最小二乘法拟合n = len(self.ref)sum_xy = sum(r * m for r, m in zip(self.ref, self.meas))sum_x = sum(self.ref)sum_y = sum(self.meas)sum_x2 = sum(r ** 2 for r in self.ref)numerator = n * sum_xy - sum_x * sum_ydenominator = n * sum_x2 - sum_x ** 2return numerator / denominatordef calibrate(self, raw_value):"""校准读数"""raw_dec = Decimal(str(raw_value))return float(raw_dec * self.calibration_factor)# 使用示例
reference = [1.0, 2.0, 3.0, 4.0, 5.0]
measured = [1.01, 2.03, 3.02, 4.06, 5.04]
calibrator = SensorCalibrator(reference, measured)raw_reading = 2.5
calibrated = calibrator.calibrate(raw_reading)
print(f"Raw: {raw_reading}, Calibrated: {calibrated:.4f}")  # Raw: 2.5, Calibrated: 2.5000

七、最佳实践与性能优化

7.1 精度与性能平衡

# 精度与性能测试
import timeitdef test_float():return 0.1 + 0.2def test_decimal():return Decimal('0.1') + Decimal('0.2')def test_fraction():return Fraction(1, 10) + Fraction(2, 10)# 性能测试
float_time = timeit.timeit(test_float, number=1000000)
decimal_time = timeit.timeit(test_decimal, number=1000000)
fraction_time = timeit.timeit(test_fraction, number=1000000)print(f"Float: {float_time:.6f}秒")
print(f"Decimal: {decimal_time:.6f}秒")
print(f"Fraction: {fraction_time:.6f}秒")

7.2 精确计算决策树

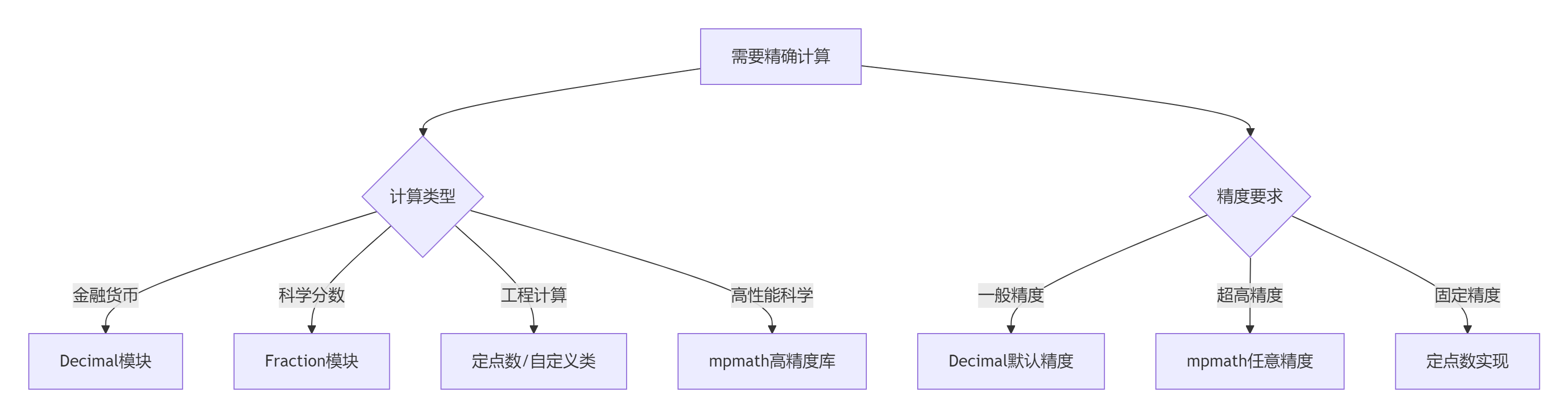
7.3 黄金实践原则

  1. ​​正确选择数据类型​​：

    # 金融计算
from decimal import Decimal
price = Decimal('99.99')# 科学分数
from fractions import Fraction
ratio = Fraction(1, 3)# 工程计算
class FixedPoint: ...

  2. ​​避免浮点数转换​​：

    # 错误做法
a = Decimal(0.1)  # 浮点数转换引入误差# 正确做法
a = Decimal('0.1')  # 字符串初始化

  3. ​​设置合理精度​​：

    # 全局精度设置
getcontext().prec = 28  # 28位有效数字# 局部精度控制
with localcontext() as ctx:ctx.prec = 50# 高精度计算

  4. ​​舍入策略选择​​：

    # 金融计算使用ROUND_HALF_UP
getcontext().rounding = ROUND_HALF_UP# 科学计算使用ROUND_HALF_EVEN
getcontext().rounding = ROUND_HALF_EVEN

  5. ​​性能优化技巧​​：

    # 批量处理减少对象创建
values = [Decimal(str(x)) for x in raw_data]
results = [x * factor for x in values]# 避免不必要的精度
getcontext().prec = 6  # 合理精度

  6. ​​错误处理机制​​：

    try:result = a / b
except DivisionByZero:handle_error()
except InvalidOperation:handle_invalid()

  7. ​​单元测试覆盖​​：

    class TestPreciseCalculations(unittest.TestCase):def test_currency_addition(self):a = Money(10.50)b = Money(20.25)self.assertEqual(a + b, Money(30.75))def test_compound_interest(self):result = compound_interest(1000, 0.05, 5)self.assertEqual(result, Decimal('1276.28'))

总结：精确小数计算技术全景

8.1 技术选型矩阵

场景推荐方案精度性能适用性
​​金融计算​​Decimal高中★★★★★
​​科学分数​​Fraction精确低★★★☆☆
​​工程计算​​定点数固定高★★★★☆
​​高性能科学​​mpmath任意低★★★☆☆
​​一般计算​​float低高★★☆☆☆

8.2 核心原则总结

  1. ​​理解问题本质​​：

    • 金融计算：Decimal优先
    • 科学实验：Fraction或mpmath
    • 工程应用：定点数或自定义类

  2. ​​避免浮点陷阱​​：

    • 永远不要用浮点数处理货币
    • 避免浮点数相等比较
    • 注意大数吃小数问题

  3. ​​精度管理策略​​：

    • 设置全局默认精度
    • 局部上下文调整精度
    • 结果量化到合理精度

  4. ​​性能优化​​：

    • 避免不必要的精度
    • 批量处理减少对象创建
    • 使用缓存优化重复计算

  5. ​​错误处理​​：

    • 处理除零错误
    • 处理无效操作
    • 处理溢出和下溢

  6. ​​测试驱动​​：

    • 边界条件测试
    • 精度验证测试
    • 性能基准测试

精确小数计算是专业开发的基石。通过掌握从基础Decimal到高级mpmath的技术体系，结合领域知识和性能优化策略，您将能够在各种应用场景中实现精确、可靠的计算结果。遵循本文的最佳实践，将使您的计算系统在金融、科学和工程领域都能表现出色。

最新技术动态请关注作者：Python×CATIA工业智造​​
版权声明：转载请保留原文链接及作者信息

http://www.xdnf.cn/news/1348219.html

相关文章：

  • 二、高可用架构（Nginx + Keepalived + MySQL 主从）
  • StarRocks启动失败——修复全流程
  • AI生成技术报告：GaussDB与openGauss的HTAP功能全面对比
  • 【COMSOL】Comsol学习案例时的心得记录分享（三）
  • 期货Level2五档订单簿0.25秒级高频分时及日频历史行情数据使用指南
  • 刷题日记0822
  • 实现自己的AI视频监控系统-第一章-视频拉流与解码4（重点）
  • uboot添加ping命令的响应处理
  • 音视频处理工作室：实时通信的媒体层设计
  • Paddle3D-PETRv1 精度测试与推理实践指南
  • 容器安全实践（一）：概念篇 - 从“想当然”到“真相”
  • 车载诊断架构 --- EOL引起关于DTC检测开始条件的思考
  • Mongodb操作指南
  • 大麦盒子DM4036-精简固件包及教程
  • 2025.8.22周五 在职老D渗透日记day24:burp+mumu抓包 安卓7.0以上证书配置
  • 电脑端完全免费的动态壁纸和屏保软件(真正免费、无广告、无会员)
  • 二叉搜索树（BST）、AVL树、红黑树
  • 爬虫基础学习-链接协议分析，熟悉相关函数
  • 基于抗辐照性能的ASP4644S电源芯片特性分析与多领域应用验证
  • 笔记本怎么才能更快散热？
  • DataStream实现WordCount
  • 信息结构统一论：物理世界与人类感知、认知及符号系统的桥梁
  • 透射TEM新手入门：衍射斑点标定 1
  • [特殊字符] TTS格局重塑！B站推出Index-TTS，速度、音质、情感表达全维度领先
  • Day25 栈 队列 二叉树
  • 特大桥施工绳断 7 人亡：索力实时监测预警机制亟待完善
  • kvcache比赛记录
  • 集群与负载均衡：HAProxy 与 Nginx 实践
  • 融云Im单独一个拍照或者拍摄插件Plugin
  • 自学嵌入式第二十五天：数据结构-队列、树