机器学习-线性回归

一、线性回归的核心思想

线性回归的本质是通过属性的线性组合来进行预测。想象一下，当我们想用房屋面积预测房价时，会寻找一条直线来最好地拟合数据；当加入房间数量、楼层等更多特征时，就需要在更高维度寻找一个 “超平面”，使得预测值与真实值的误差最小化。

线性模型的一般形式可以表示为：
f(x)=w1​x1​+w2​x2​+...+wd​xd​+b
其中，x1​,x2​,...,xd​是样本的d个特征，w1​,w2​,...,wd​是对应的权重（系数），b是偏置项（截距）。用向量形式可简化为：f(x)=wTx+b，这里w是权重向量，x是特征向量。

权重w反映了对应特征对预测结果的影响程度：正值表示正相关（特征值越大，预测值越大），负值表示负相关，绝对值越大影响越显著。偏置项b则是当所有特征值为 0 时的基准预测值。

二、最优的线性模型—— 最小二乘法

确定线性模型的关键是求解最优的w和b，而最小二乘法是实现这一目标的经典方法。它的核心思想是：找到一条直线（或超平面），使所有样本到直线的欧氏距离之和最小。

从数学角度看，就是最小化均方误差（MSE）。定义损失函数E(w,b)为所有样本预测误差的平方和：
E(w,b)=∑i=1m​(yi​−f(xi​))2=∑i=1m​(yi​−(wxi​+b))2
其中m是样本数量，yi​是真实值，f(xi​)是预测值。

求解过程分为两步：

1. 对w和b分别求偏导，得到损失函数的变化率；
2. 令偏导数为 0，解方程组得到最优参数w和b的解析解。

这一过程被称为线性回归模型的参数估计，最终得到的w和b能使损失函数E(w,b)达到最小值。

三、评估模型好坏—— 关键指标解析

训练好模型后，需要通过评估指标判断其性能。线性回归常用的评估指标有以下三种：

1. 误差平方和（SSE/RSS）

SSE（Sum of Squared Errors）也称为残差平方和，计算公式为：
SSE=∑i=1m​(yi​−y^​i​)2
其中y^​i​是预测值。SSE 直接衡量了所有样本预测误差的平方总和，值越小说明模型拟合效果越好。

2. 均方误差（MSE）

MSE（Mean Square Error）是 SSE 的平均值，计算公式为：
MSE=m1​∑i=1m​(yi​−y^​i​)2
MSE 消除了样本数量对误差的影响，更直观地反映平均误差大小，单位是目标变量单位的平方。

3. 决定系数（R²）

R² 是最常用的评估指标之一，计算公式为：
R2=1−SSTSSE​=1−∑(yi​−yˉ​)2∑(yi​−y^​i​)2​
其中SST是总平方和（反映真实值的总变异），yˉ​是真实值的平均值。

R² 的取值范围在(−∞,1]：

• 越接近 1，说明模型对数据的解释能力越强，拟合效果越好；
• 若 R²=0，说明模型效果与直接用平均值预测相当；
• 若 R²<0，则说明模型效果比随机猜测更差。

四、从单变量到多变量 —— 多元线性回归

当特征数量不止一个时，就需要用到多元线性回归。其模型形式为：
f(x)=w0​+w1​x1​+w2​x2​+...+wn​xn​
其中w0​是偏置项（可视为x0​=1时的权重），x1​,x2​,...,xn​是n个特征。

多元线性回归的求解原理与单变量类似，同样通过最小二乘法估计参数，但计算过程更复杂，通常需要借助矩阵运算。在实际应用中，我们无需手动计算，可直接使用机器学习库（如 scikit-learn）中的线性回归工具。

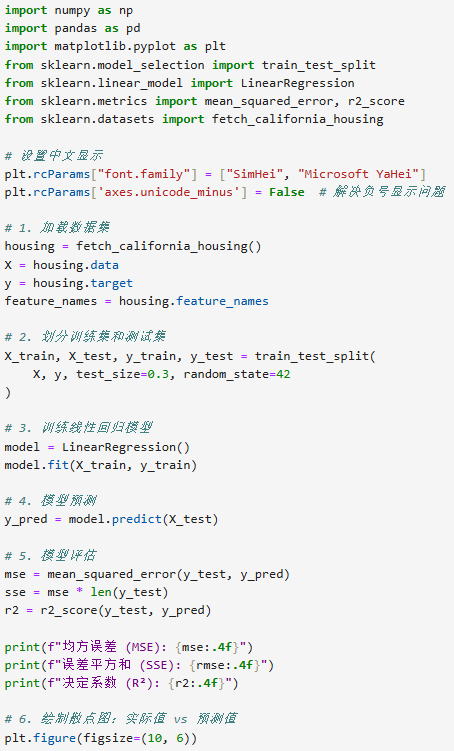
五、总结

线性回归作为最简单的监督学习模型之一，却蕴含着丰富的统计学思想。它通过最小二乘法求解最优参数，用 SSE、MSE 和 R² 等指标评估性能，既能处理单变量问题，也能扩展到多元场景。

虽然线性回归假设特征与目标变量是线性关系，在复杂场景下可能表现有限，但它胜在解释性强、计算高效，是数据分析和建模的基础工具。无论是预测房价、股票走势，还是分析影响因素，线性回归都能为我们提供有价值的 insights。