计数组合学7.20(平面分拆与RSK算法)
7.20 平面分拆与RSK算法
我们现在已经发展了足够多的对称函数理论,可以给出一些计数应用。本节和接下来的两节将致力于讨论整数分拆的一个引人入胜的推广,称为“平面分拆”。一个平面分拆(plane partition)是一个非负整数数组 π=(πij)i,j≥1\pi = (\pi_{ij})_{i,j \geq 1}π=(πij)i,j≥1,满足 π\piπ 具有有限支集(即只有有限多个非零项)且在行和列上弱递减。如果 ∑πij=n\sum \pi_{ij} = n∑πij=n,那么我们记 ∣π∣=n|\pi| = n∣π∣=n 并称 π\piπ 是 nnn 的一个平面分拆。在书写平面分拆的例子时,0(或除有限个以外的所有0)被省略。因此,整数 0≤n≤30 \leq n \leq 30≤n≤3 的平面分拆由下式给出:
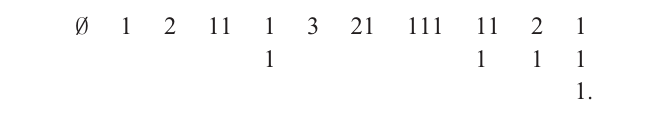
一个普通分拆 λ⊢n\lambda \vdash nλ⊢n 可以看作是一个具有有限支集的非负整数的弱递减一维数组 (λ1,λ2,…)(\lambda_1, \lambda_2, \ldots)(λ1,λ2,…)。因此平面分拆是普通分拆在二维的自然推广。现在似乎很自然地可以为任意 r≥1r \geq 1r≥1 定义 rrr 维分拆。然而,对于 r≥3r \geq 3r≥3 几乎没有任何重要结果。平面分拆与半标准杨表有明显的相似之处。实际上,一个反半标准杨表(reverse SSYT)就是一种特殊的平面分拆(移除了无关的0),事实上,在我们定义反半标准杨表时,我们提到了另一个术语“列严格平面分拆”。由于半标准杨表与平面分拆之间的相似性,对称函数在平面分拆的计数中扮演重要角色也就不足为奇了。
平面分拆 π=(πij)\pi = (\pi_{ij})π=(πij) 的一个部分(part)是一个正的项 πij>0\pi_{ij} > 0πij>0。π\piπ 的形状(shape)是一个普通分拆 λ\lambdaλ,其中 π\piπ 在第 iii 行有 λi\lambda_iλi 个非零部分(所以 πiλi>0,πi,λi+1=0\pi_{i\lambda_i} > 0, \pi_{i,\lambda_i+1} = 0πiλi>0,πi,λi+1=0)。如果 r=ℓ(λ)r = \ell(\lambda)r=ℓ(λ),我们说 π\piπ 有 rrr 行(rows)。类似地,如果 s=ℓ(λ′)=λ1s = \ell(\lambda') = \lambda_1s=ℓ(λ′)=λ1,则 π\piπ 有 sss 列(columns)。记 ℓ1(π)\ell_1(\pi)ℓ1(π) 为 π\piπ 的行数,ℓ2(π)\ell_2(\pi)ℓ2(π) 为列数。最后用通常的公式 tr(π)=∑πii\operatorname{tr}(\pi) = \sum \pi_{ii}tr(π)=∑πii 定义 π\piπ 的迹(trace)。例如,平面分拆:
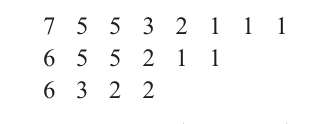
具有形状 (8, 6, 4),18个部分,3行,8列,迹为14。
令 P(r,c)\mathcal{P}(r, c)P(r,c) 为所有最多 rrr 行和最多 ccc 列的平面分拆的集合。例如,如果 π∈P(1,c)\pi \in \mathcal{P}(1, c)π∈P(1,c),那么 π\piπ 就是一个普通分拆,且 tr(π)\text{tr}(\pi)tr(π) 是 π\piπ 的最大部分。通过“观察”(观察共轭分拆 π′\pi'π′ 而不是 π\piπ)可以清楚地看出:
∑π∈P(1,c)qtr(π)x∣π∣=1(1−qx)(1−qx2)⋯(1−qxc).(7.98)\sum_{\pi \in \mathcal{P}(1, c)} q^{\text{tr}(\pi)} x^{|\pi|} = \frac{1}{(1 - qx)(1 - qx^2) \cdots (1 - qx^c)}. \tag{7.98}π∈P(1,c)∑qtr(π)x∣π∣=(1−qx)(1−qx2)⋯(1−qxc)1.(7.98)
本节的主要结果是以下方程 (7.98) 的推广。
7.20.1 定理
固定 r,c∈Pr, c \in \mathbb{P}r,c∈P。则
∑π∈P(r,c)qtr(π)x∣π∣=∏i=1r∏j=1c(1−qxi+j−1)−1.\sum_{\pi \in \mathcal{P}(r, c)} q^{\text{tr}(\pi)} x^{|\pi|} = \prod_{i=1}^r \prod_{j=1}^c \left( 1 - qx^{i+j-1} \right)^{-1}.π∈P(r,c)∑qtr(π)x∣π∣=i=1∏rj=1∏c(1−qxi+j−1)−1.
证明. 我们将基于 RSK 算法以及一种将一对同形状的反半标准杨表合并成单个平面分拆的简单方法,给出一个优雅的双射证明。首先我们描述如何将两个具有互异部分且部分数相同的分拆 λ\lambdaλ 和 μ\muμ 合并成一个分拆 ρ=ρ(λ,μ)\rho = \rho(\lambda, \mu)ρ=ρ(λ,μ)。画出 λ\lambdaλ 的 Ferrers 图,但每一行都从前一行的开头向右缩进一个空格。这样的图称为 λ\lambdaλ 的移位 Ferrers 图(shifted Ferrers diagram)。例如,如果 λ=(5,3,2)\lambda = (5, 3, 2)λ=(5,3,2),那么我们得到移位图:

对 μ\muμ 做同样操作,然后转置该图。例如,如果 μ=(6,3,1)\mu = (6, 3, 1)μ=(6,3,1),那么我们得到转置移位图:
外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传
现在通过识别它们的主对角线将两个图合并成一个图。对于上面的 λ\lambdaλ 和 μ\muμ,我们得到图(为清晰起见画出主对角线):
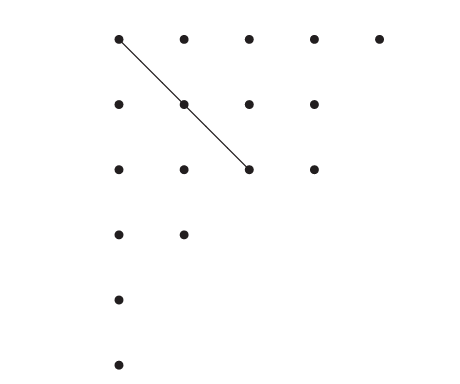
定义 ρ(λ,μ)\rho(\lambda,\mu)ρ(λ,μ) 为一个分拆,使得这个合并图是其 Ferrers 图。上面的例子表明:
ρ(532,631)=544211.\rho(532,631) = 544211.ρ(532,631)=544211.
映射 (λ,μ)↦ρ(λ,μ)(\lambda,\mu) \mapsto \rho(\lambda,\mu)(λ,μ)↦ρ(λ,μ) 显然是具有 kkk 个互异部分的分拆对 (λ,μ)(\lambda,\mu)(λ,μ) 与秩为 kkk 的分拆 ρ\rhoρ(如 1.8 节和 7.2 节所定义)之间的双射。注意:
∣ρ∣=∣λ∣+∣μ∣−ℓ(λ).|\rho| = |\lambda| + |\mu| - \ell(\lambda).∣ρ∣=∣λ∣+∣μ∣−ℓ(λ).
我们现在将上述双射扩展到同形状的反半标准杨表对 (P,Q)(P,Q)(P,Q)。如果 λi\lambda^iλi 表示 PPP 的第 iii 列,μi\mu^iμi 表示 QQQ 的第 iii 列,那么令 π(P,Q)\pi(P,Q)π(P,Q) 为一个数组,其第 iii 列是 ρ(λi,μi)\rho(\lambda^i,\mu^i)ρ(λi,μi)。例如,如果
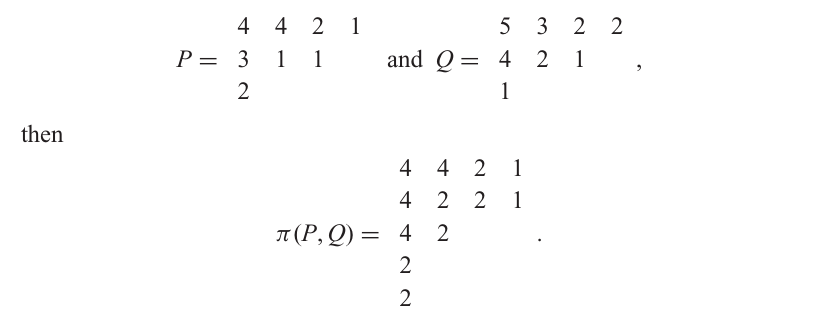
容易看出 π(P,Q)\pi(P,Q)π(P,Q) 是一个平面分拆。将 π(P,Q)\pi(P,Q)π(P,Q) 的每一行取其共轭,得到另一个平面分拆 π′(P,Q)\pi'(P,Q)π′(P,Q)。对于上面的 π(P,Q)\pi(P,Q)π(P,Q),我们得到:
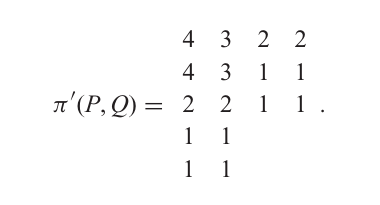
可以很容易地验证,映射 (P,Q)↦π′(P,Q)(P, Q) \mapsto \pi'(P, Q)(P,Q)↦π′(P,Q) 是同形状的反半标准杨表对 (P,Q)(P, Q)(P,Q) 与平面分拆 π′\pi'π′ 之间的双射。记 diag(π′)\text{diag}(\pi')diag(π′) 为 π′\pi'π′ 的主对角线 (π11′,π22′,…)(\pi_{11}', \pi_{22}', \ldots)(π11′,π22′,…),max(P)\max(P)max(P) 为反半标准杨表 PPP 的最大部分 P11P_{11}P11,等等。回忆 sh(P)\text{sh}(P)sh(P) 表示 PPP 的形状,所以 sh(P)=sh(Q)\text{sh}(P) = \text{sh}(Q)sh(P)=sh(Q),其中 P,QP, QP,Q 如上所述。容易看出:
∣π′∣=∣P∣+∣Q∣−∣sh(P)∣(7.99)|\pi'| = |P| + |Q| - |\text{sh}(P)| \tag{7.99}∣π′∣=∣P∣+∣Q∣−∣sh(P)∣(7.99)
diag(π′)=sh(P)=sh(Q),所以tr(π′)=∣sh(P)∣\text{diag}(\pi') = \text{sh}(P) = \text{sh}(Q), \quad \text{所以} \quad \text{tr}(\pi') = |\text{sh}(P)|diag(π′)=sh(P)=sh(Q),所以tr(π′)=∣sh(P)∣
ℓ1(π′)=max(Q)\ell_1(\pi') = \max(Q)ℓ1(π′)=max(Q)
ℓ2(π′)=max(P).\ell_2(\pi') = \max(P).ℓ2(π′)=max(P).
现在令 A=(aij)A = (a_{ij})A=(aij) 是一个具有有限支集的 N\mathbb{N}N-矩阵。我们希望将 AAA 与一对同形状的反半标准杨表相关联。这可以通过 RSK 算法的一个明显变体来完成,其中我们在定义行插入时反转了 ≤\leq≤ 和 ≥\geq≥ 的角色。等价地,如果 wA=(u1⋯unv1⋯vn)w_A = \binom{u_1 \cdots u_n}{v_1 \cdots v_n}wA=(v1⋯vnu1⋯un) 是与 AAA 关联的双行数组,那么将普通的 RSK 算法应用于双行数组 (−un⋯−u1−vn⋯−v1)\binom{-u_n \cdots -u_1}{-v_n \cdots -v_1}(−vn⋯−v1−un⋯−u1)(其条目现在是负整数),然后将这对半标准杨表的所有条目的符号改回正号。我们将得到一对反半标准杨表 (P,Q)(P, Q)(P,Q),满足:
∣P∣=∑i,jjaij(7.100)|P| = \sum_{i,j} ja_{ij} \tag{7.100}∣P∣=i,j∑jaij(7.100)
∣Q∣=∑i,jiaij|Q| = \sum_{i,j} ia_{ij}∣Q∣=i,j∑iaij
max(P)=max{j:aij≠0}\max(P) = \max\{j : a_{ij} \neq 0\}max(P)=max{j:aij=0}
max(Q)=max{i:aij≠0}\max(Q) = \max\{i : a_{ij} \neq 0\}max(Q)=max{i:aij=0}
∣sh(P)∣=∣sh(Q)∣=∑aij.|\text{sh}(P)| = |\text{sh}(Q)| = \sum a_{ij}.∣sh(P)∣=∣sh(Q)∣=∑aij.
由以 (7.99) 和 (7.100) 开始的方程组可知,如果 Mrc\mathcal{M}_{rc}Mrc 是所有 r×cr \times cr×c N\mathbb{N}N-矩阵的集合,那么:
∑π∈P(r,c)qtr(π)x∣π∣=∑A=(aij)∈Mrcq∑aijx∑(i+j)aij−∑aij\sum_{\pi \in \mathcal{P}(r,c)} q^{\text{tr}(\pi)} x^{|\pi|} = \sum_{A=(a_{ij}) \in \mathcal{M}_{rc}} q^{\sum a_{ij}} x^{\sum (i+j) a_{ij} - \sum a_{ij}}π∈P(r,c)∑qtr(π)x∣π∣=A=(aij)∈Mrc∑q∑aijx∑(i+j)aij−∑aij
=∏i=1r∏j=1c(∑aij≥0qaijx(i+j−1)aij)= \prod_{i=1}^{r} \prod_{j=1}^{c} \left( \sum_{a_{ij} \geq 0} q^{a_{ij}} x^{(i+j-1) a_{ij}} \right)=i=1∏rj=1∏caij≥0∑qaijx(i+j−1)aij
=∏i=1r∏j=1c(1−qxi+j−1)−1.= \prod_{i=1}^{r} \prod_{j=1}^{c} \left( 1 - q x^{i+j-1} \right)^{-1}.=i=1∏rj=1∏c(1−qxi+j−1)−1.
现在令 P(r)\mathcal{P}(r)P(r) 表示所有最多 rrr 行的平面分拆的集合。如果在定理 7.20.1 中令 q=1q=1q=1 且 c→∞c\to\inftyc→∞,那么我们得到 P(r)\mathcal{P}(r)P(r) 中元素的以下优雅计数。
7.20.2 推论
固定 r∈Pr\in\mathbb{P}r∈P。则
∑π∈P(r)x∣π∣=∏i≥1(1−xi)−min(i,r).(7.101)\sum_{\pi\in\mathcal{P}(r)}x^{|\pi|}=\prod_{i\geq 1}\left(1-x^{i}\right)^{-\min \left(i,r\right)}. \tag{7.101}π∈P(r)∑x∣π∣=i≥1∏(1−xi)−min(i,r).(7.101)
证明. 定理 7.20.1 给出:
∑π∈P(r)x∣π∣=∏i=1r∏j≥1(1−xi+j−1)−1,\sum_{\pi\in\mathcal{P}(r)}x^{|\pi|}=\prod_{i=1}^{r}\prod_{j\geq 1}\left(1-x^{i+j-1}\right)^{-1},π∈P(r)∑x∣π∣=i=1∏rj≥1∏(1−xi+j−1)−1,
容易看出这与 (7.101) 的右侧一致。 □
最后令 P\mathcal{P}P 表示所有平面分拆的集合,并在推论 7.20.2 中令 r→∞r\to\inftyr→∞,得到平面分拆理论中的原型结果:
7.20.3 推论
我们有
∑π∈Px∣π∣=∏i≥1(1−xi)−i.\sum_{\pi\in\mathcal{P}}x^{|\pi|}=\prod_{i\geq 1}\left(1-x^{i}\right)^{-i}.π∈P∑x∣π∣=i≥1∏(1−xi)−i.
当我们考虑 RSK 算法的对称性结果定理 7.13.1 时,定理 7.20.1 的一个很好的变体就出现了。定义一个平面分拆 σ=(σij)\sigma=(\sigma_{ij})σ=(σij) 是对称的(symmetric),如果对所有 i,ji,ji,j 有 σij=σji\sigma_{ij}=\sigma_{ji}σij=σji。令 S(r)\mathcal{S}(r)S(r) 表示所有最多 rrr 行(因此也最多 rrr 列)的对称平面分拆的集合。
7.20.4 定理
固定 r∈Pr\in\mathbb{P}r∈P。则
∑σ∈S(r)qtr(σ)x∣σ∣=∏i=1r(1−qx2i−1)−1⋅∏1≤i<j≤r(1−q2x2(i+j−1))−1.\sum_{\sigma\in\mathcal{S}(r)}q^{\mathrm{tr}(\sigma)}x^{|\sigma|}=\prod_{i=1}^{r}\left(1-qx^{2i-1}\right)^{-1}\cdot \prod_{1\leq i<j\leq r}\left(1-q^{2}x^{2(i+j-1)}\right)^{-1}.σ∈S(r)∑qtr(σ)x∣σ∣=i=1∏r(1−qx2i−1)−1⋅1≤i<j≤r∏(1−q2x2(i+j−1))−1.
第一个证明. 令 π′(P,Q)\pi^{\prime}(P,Q)π′(P,Q) 是定理 7.20.1 证明中描述的平面分拆。容易看出 π′\pi^{\prime}π′ 是对称的当且仅当 P=QP=QP=Q。此外,假设 A→RSK′(P,Q)A \xrightarrow{\text{RSK}^{\prime}} (P,Q)ARSK′(P,Q),其中 RSK′\text{RSK}^{\prime}RSK′ 也是在定理 7.20.1 证明中描述的“反向”RSK 算法(所以 PPP 和 QQQ 是反半标准杨表)。定理 7.13.1 同样适用于 RSK′\text{RSK}^{\prime}RSK′,所以 A→RSK′(P,P)A \xrightarrow{\text{RSK}^{\prime}} (P,P)ARSK′(P,P) 当且仅当 A=A′A=A^{\prime}A=A′。令 Mr′\mathcal{M}_{r}^{\prime}Mr′ 是所有 r×rr\times rr×r 对称 N\mathbb{N}N-矩阵的集合。然后我们完全类似于定理 7.20.1 的证明,得到:
第二个证明. 有一个巧妙的替代证明避免了使用定理 7.13.1。假设 π\piπ 是一个只有奇数部分的反半标准杨表。因此 π\piπ 的每一列都是互异奇数部分的分拆。命题 1.8.4 的证明给出了 nnn 的具有互异奇数部分的分拆与 nnn 的自共轭分拆之间的双射。将此双射应用于 π\piπ 的每一列,然后取每一行的共轭,产生一个对称平面分拆 σ\sigmaσ。一个例子由下式给出:

可以容易地验证 ∣π∣=∣σ∣|\pi| = |\sigma|∣π∣=∣σ∣,sh(π)=diag(σ)\text{sh}(\pi) = \text{diag}(\sigma)sh(π)=diag(σ),∣sh(π)∣=tr(σ)|\text{sh}(\pi)| = \text{tr}(\sigma)∣sh(π)∣=tr(σ),以及 ℓ1(σ)=12(1+max(π))\ell_1(\sigma) = \frac{1}{2}(1 + \max(\pi))ℓ1(σ)=21(1+max(π))。因此由推论 7.13.8 可得:
∑σ∈S(r)qtr(σ)x∣σ∣=∏i=1i odd2r−1(1−xi)−1⋅∏1≤i<j≤2r−1ij odd(1−xixj)−1∣xi=qxi\sum_{\sigma \in \mathcal{S}(r)} q^{\text{tr}(\sigma)} x^{|\sigma|} = \prod_{\substack{i=1 \\ i \text{ odd}}}^{2r-1} (1 - x_i)^{-1} \cdot \prod_{\substack{1 \leq i < j \leq 2r-1 \\ ij \text{ odd}}} (1 - x_i x_j)^{-1} \bigg|_{x_i = q x^i}σ∈S(r)∑qtr(σ)x∣σ∣=i=1i odd∏2r−1(1−xi)−1⋅1≤i<j≤2r−1ij odd∏(1−xixj)−1xi=qxi
=∏i=1r(1−qx2i−1)−1⋅∏1≤i<j≤r(1−q2x2(i+j−1))−1.□= \prod_{i=1}^r \left( 1 - q x^{2i-1} \right)^{-1} \cdot \prod_{1 \leq i < j \leq r} \left( 1 - q^2 x^{2(i+j-1)} \right)^{-1}. \quad \square=i=1∏r(1−qx2i−1)−1⋅1≤i<j≤r∏(1−q2x2(i+j−1))−1.□
令 q=1q = 1q=1 且 r→∞r \to \inftyr→∞,得到所有 nnn 的对称平面分拆的以下优雅计数。
7.20.5 推论
令 S\mathcal{S}S 为所有对称平面分拆的集合。则
∑σ∈Sx∣σ∣=∏i≥11(1−x2i−1)(1−x2i)[i/2].\sum_{\sigma \in \mathcal{S}} x^{|\sigma|} = \prod_{i \geq 1} \frac{1}{\left( 1 - x^{2i-1} \right) \left( 1 - x^{2i} \right)^{[i/2]}}.σ∈S∑x∣σ∣=i≥1∏(1−x2i−1)(1−x2i)[i/2]1.
