Codeforces1043 A至F 题解

22:13：登录进 Codeforces。

22:15：登录进洛谷，发现今日忌睡觉：

22:35：比赛开始，打开了 A 题。

22:37：发现 Google 翻译太难用了，于是换成了 AI 翻译。

22:38：发现 A 题是一道水题，题面如下：

很明显，直接暴力你就可以得到一个 $O(tm)$ 的“高效”做法。

22:41：写完并调试完代码，直接 AC。

代码：

#include<bits/stdc++.h>
#define int long long
#define code using
#define by namespace
#define plh std
code by plh;
int t,n,m;
string s1,s2,s3;
signed main()
{cin>>t;while(t--){cin>>n;cin>>s1;cin>>m;cin>>s2>>s3;string ans="";for(int i=m-1;i>=0;i--){if(s3[i]=='V'){ans+=s2[i];}}ans+=s1;for(int i=0;i<m;i++){if(s3[i]=='D'){ans+=s2[i];}}cout<<ans<<'\n';}return 0;
}

22:42：打开 B 题，发现又是一道水题。

题面：

因为往一个数后面加 $0$ 实际上就是给这个数乘了一个 $10^k$，所以新得到的这个数就是 $x+x\times 10^k=x\times (10^k+1)$，那明显 $k$ 是可以枚举的（因为顶天了也就枚举 $\lg (n)$ 次），然后看看 $n$ 能不能整除 $10^k+1$，如果能，就整除后把得到的值记录下来，最后排个序输出一下就好了（在这里为了方便，我用的 set 排序，主要是正常的 sort 是 $O(n{\log }_2(n))$，而 set 则是 $O({\log }_2(n))$ 的，这样可以防止 TLE）。

22:46：写完并调试完 B 题代码，直接提交 AC。

代码：

#include<bits/stdc++.h>
#define int long long
#define code using
#define by namespace
#define plh std
code by plh;
int t,n;
signed main()
{cin>>t;while(t--){cin>>n;int k=1;set<int>s;while(k+1<=n){k*=10;if(n%(k+1)==0){s.insert(n/(k+1));}}cout<<s.size()<<'\n';for(auto i:s){cout<<i<<" ";}if(s.size()!=0){cout<<'\n';}}return 0;
}

22:47：打开 C1 题，猜出用三进制解。

题面：

22:50：纠结是否用三进制写。

22:54：决定直接写代码，懒得证明。

因为小贩每次只能卖出 $3^x$ 西瓜，所以很明显：这题是让我们把 $n$ 分解成 $a_1\times 3^{x_1}+a_2\times 3^{a_2}\cdots +a_k\times 3^{x_k}$，并且要求 ${\sum }_{i=1}^k{a}_i$ 要最小。那很容易想到把 $n$ 三进制分解了，再按每一位的值（$a_i$）计算花的金币个数（当然这是我猜的，具体原因我也没证出来为什么这样 ${\sum }_{i=1}^k{a}_i$ 最小）。

我想起了我们同学的一句话：大胆猜想，不用证明！（不值得借鉴）于是我就凭直觉写了份代码，然后 AC 了。

23:02：C1 题 AC 了。

代码：

#include<bits/stdc++.h>
#define int long long
#define code using
#define by namespace
#define plh std
code by plh;
int t,n,a[26],b[26];
signed main()
{b[0]=1;for(int i=1;i<=20;i++){b[i]=b[i-1]*3;}a[0]=b[1];for(int i=1;i<20;i++){a[i]=b[i+1]+i*b[i-1];}cin>>t;while(t--){int ans=0,pos=0;cin>>n;while(n){ans+=(n%3)*a[pos];n/=3;pos++;}cout<<ans<<'\n';}return 0;
}

23:03：打开 C2 题，发现就是把 C1 题改变了一下。

题面：

对于这题，我们首先要从收金币的式子入手：

$$3^{x+1}+x\cdot 3^{x-1}$$

我们看看进行三次买 $3^{x-1}$ 个西瓜的操作和进行一次买 $3^x$ 个西瓜的操作所花的金币有什么区别：

• 买了三次 $3^{x-1}$ 的西瓜：

$$3\times (3^x+(x-1)\cdot 3^{x-2})=3^{x+1}+(x-1)\cdot 3^{x-1}$$

• 买了一次 $3^x$ 个西瓜：

$$3^{x+1}+x\cdot 3^{x-1}$$

仔细一对比就不难发现：买三次 $3^{x-1}$ 个西瓜比买一次 $3^x$ 个西瓜要便宜 $3^{x-1}$ 个金币 （生活小妙招，你值得拥有），那我们现在要让价格最低，就是要让我们能便宜的钱最多，很明显，$3^{x-1}$ 这个指数型函数是单调递增的，所以 $x$ 越大，$3^{x-1}$ 也就越大，所以综上：我们就是要尽量的用小的西瓜的个数代替大的西瓜的个数，并且大的个数越大越好。

那么我们在 C1 题的代码上改变一下：用一个数组记录一下三进制分解完后的数，然后从高位到低位尽量的把数往下传，最后算答案。

23:22：AC 了 C2 题。

代码：

#include<bits/stdc++.h>
#define int long long
#define code using
#define by namespace
#define plh std
code by plh;
int t,n,k,a[26],b[26],c[26];
signed main()
{b[0]=1;for(int i=1;i<=20;i++){b[i]=b[i-1]*3;}a[0]=b[1];for(int i=1;i<20;i++){a[i]=b[i+1]+i*b[i-1];}cin>>t;while(t--){int ans=0,pos=0,cnt=0;cin>>n>>k;while(n){c[++pos]=n%3;cnt+=c[pos];n/=3;}if(cnt>k){cout<<-1<<'\n';}else if(cnt==k){for(int i=1;i<=pos;i++){ans+=c[i]*a[i-1];}cout<<ans<<'\n';}else{for(;pos>1&&cnt+c[pos]*2<=k;){c[pos-1]+=c[pos]*3;cnt+=c[pos]*2;c[pos]=0;pos--;}if(pos>1){c[pos]-=(k-cnt)/2;c[pos-1]+=(k-cnt)/2*3;}for(int i=1;i<=pos;i++){ans+=c[i]*a[i-1];}cout<<ans<<'\n';}}return 0;
}

23:33：打开了 D 题，发现是一道毒瘤数学题。

然后就推了一个小时的数学公式。

最终时间复杂度：$O(t)$ 左右（可能带个小常数）。

首先先声明：我的做法有点与众不同，也有点抽象，请谨慎观看。

首先我们肯定要确定最后一个数是什么，那在这之前因为我们有的只是前面几项的数字位数之和，所以我们要先解决最后一个数是多少位这个问题。

我们先来做个小统计：

• 一位数的个数：$9$ 个。
• 两位数的个数：$90$ 个。
• 三位数的个数：$900$ 个。
• $d$ 位数的个数：$9\times 10^{d-1}$

然后我们求一下到第 $d$ 位数字一共有多少位数：

$$1\times 9+2\times 90+3\times 900\cdots +d\times 10^{d-1}$$

本来到这暴力枚举就行了，但闲不下来的作者非要搞事情，于是我把这个式子设成了 $S$，即：

$$S=\sum _{i=1}^{d}9\times i\times 10^{i-1}$$

提个公因数：

$$S=9\times \sum _{i=1}^{d}i\times 10^{i-1}$$

然后把后半部分设成一个新的函数 $T$，则：

$$T=\sum _{i=1}^{d}i\times 10^{i-1}$$

然后我们试着用数学公式把 $T$ 表示出来。

首先对 $T$ 乘以一个 $10$：

$$10T=\sum _{i=1}^{d}i\times 10^i$$

两式相减得：

$$9T=d\times 10^d-10^0-10^1-10^2-\cdots -10^{d-1}$$\

看到这让我想起了一个数竞里的公式：

$$a^n-b^n=(a-b)(a^{n-1}+a^{n-1}b+\cdots +b^{n-1})$$

于是我干了这么一件事：

$$9T=d\times 10^d-(10^0+10^1+\cdots +10^{d-1})$$

$$81T=9\times d\times 10^d-(10-1)(10^0+10^1+\cdots +10^{d-1})$$

$$81T=(10-1)\times d\times 10^d-(10^d-1)$$

$$81T=d\times 10^{d+1}-d\times 10^d-10^d+1$$

$$81T=d\times 10^{d+1}-(d+1)\times 10^d+1$$

$$T=\frac{d\times 10^{d+1}-(d+1)\times 10^d+1}{81}$$

然后我们不难发现：这个 $10$ 的幂是可以预处理的，这个 $T$本身也是可以证明出来是单调递增的，于是我们可以使用二分查找 $d$ 的值，然后带进去看看当前的总位数是否 $\ge k$，这样下来时间复杂度就优化了一个 $\log$。

接下来就是算最后一个数字了，这里我不过多讲怎么算（笑话，位数都给你了，还能算不出来），不会的自己看代码。

然后再算 $k$ 指向的是最后一个数字的哪一位，这里也不过多讲，不会的看代码。

最终到了统计环节，很容易想到用一个数位 DP 就可以解决，但爱整花活的作者偏不。我先把最后一个数字单独统计了一下（因为最后一个数字不是所有数位都要），然后就开始算从 $1\to ed-1$ 的每一位的值的和。

我是这样做的：首先把一个数字拆成三部分：高位（h）、当前要计数的位（m）和低位（l）。

然后我们就看看那个当前计数的位能贡献出多少的值来。

首先如果高位取的值是 $0\to h-1$，那么当前这一位是 $0\to 9$ 随便选的，而且低位也是：

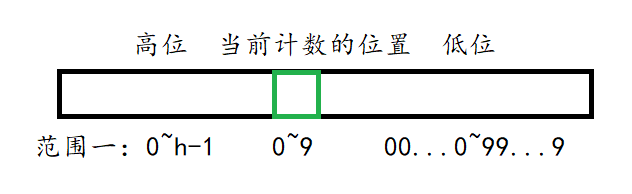
这时不难发现：高位一共有 $h$ 种情况，低位一共有 $10^d$（其中 $d$ 表示低位的位数）种情况，而当前的位置是 $0\to 9$ 随便选的，共计贡献 $45$，而这种情况一共有 $h\times 10^d$ 个，所以第一种情况的答案就是 $45\times h\times 10^d$。

其次就是高位取得 $h$，那么当前这一位可以取 $0\to m-1$，用高斯求和公式就可以知道贡献是 $\frac{m(m-1)}{2}$，而低位还是 $10^d$ 种情况随便选，因此这种情况的贡献是 $\frac{m(m-1)}{2}\times 10^d$。

最后就是中间那一位也是 $m$，那么低位就只能选 $0\to l$ 了，一共 $l+1$ 种情况，而这是中间那一位数只能取 $m$，所以此时贡献是 $m(l+1)$。

综上，对于当前这一位的总贡献是 $45h\times 10^d+\frac{m(m-1)}{2}\times 10^d+m(l+1)$。这下又省了点空间复杂度。

然后就可以码代码了。

00:45：推出所有公式并写完代码，最后一发直接 AC。

代码：

#include<bits/stdc++.h>
#define int long long
#define code using
#define by namespace
#define plh std
code by plh;
int t,k;
int T(int x)
{int p=1,q=1;for(int i=1;i<=x+1;i++){p*=10;q*=10;}q/=10;p*=x;q*=(x+1);p-=q;p++;int r=p/81;return r;
}
int S(int x)
{return 9*T(x);
}
int qpow(int x,int y)
{int z=1;for(int i=1;i<=y;i++){z*=x;}return z;
}
int sum(int x)
{if(x==0){return 0;}int p=1,ans=0;for(;p<=x;p*=10){int h=x/(p*10);int m=x/p%10;int l=x%p;ans+=h*p*45;ans+=m*(m-1)/2*p;ans+=(l+1)*m;}return ans;
}
signed main()
{cin>>t;while(t--){cin>>k;int l=1,r=20,d=0,ans=0;while(l<=r){int mid=l+r>>1;if(S(mid)>=k){r=mid-1;d=mid;}else{l=mid+1;}}int pre=S(d-1);int oth=k-pre;int ed=(oth-1)/d+qpow(10,d-1);int pos=(oth-1)%d;string s=to_string(ed);for(int i=0;i<=pos;i++){ans+=(s[i]-'0');}cout<<ans+sum(ed-1)<<'\n';}return 0;
}

然后比赛结束了。

至于 E 题，是比赛结束后我再打的，这里也简单讲一下。

首先我们要让综合最大，用点贪心思想就知道肯定要从大到小排序，然后尽量选大的，因此我们做一个前缀和。

现在我们有了两个前缀和 $prea,preb$，我们假设从 a 中选出了 $i$ 个数，那 $b$ 中就只能选 $z-i$ 个数，所以我们就是要求 max⁡{preai+prebz−i}\max\{prea_i+preb_{z-i}\}max{preai​+prebz−i​}。

那 $i$ 的范围怎么求呢？

很明显，$i$ 要满足两个条件：

{0≤i≤min⁡{z,x}0≤z−i≤min⁡{z,y}\begin{cases}0\le i\le\min\{z,x\}\\0\le z-i\le\min\{z,y\}\end{cases}{0≤i≤min{z,x}0≤z−i≤min{z,y}​

我们对第二个式子移一下项就可以得到：

i≥max⁡{0,z−y}i\ge\max\{0,z-y\}i≥max{0,z−y}

于是 $i$ 的范围就是 max⁡{0,z−y}≤i≤min⁡{z,x}\max\{0,z-y\}\le i\le\min\{z,x\}max{0,z−y}≤i≤min{z,x}。

如果你直接暴力枚举这个区间，你会获得一个大大的 TLE（不要问我怎么知道的）。

因此我们需要优化它，怎么优化呢？

看到标签中的三分，我突然灵光一闪：可不可以用三分解？

简单证明了一下函数单调性，发现可以（这里留给读者自己去证，如果没学过三分，自己去查资料）！

于是我们可以使用三分优化缩小这个区间再暴力枚举（我这里定的范围缩小到差小于等于 $5$）。

于是就可以完美的 AC 这道题了。

代码：

#include<bits/stdc++.h>
#define int long long
#define code using
#define by namespace
#define plh std
code by plh;
int t,n,m,q;
signed main()
{cin>>t;while(t--){cin>>n>>m>>q;vector<int>a(n+6);vector<int>b(m+6);for(int i=0;i<n;i++){cin>>a[i];}for(int i=0;i<m;i++){cin>>b[i];}sort(a.begin(),a.end(),[&](int x,int y){return x>y;});sort(b.begin(),b.end(),[&](int x,int y){return x>y;});vector<int>s1(n+6);vector<int>s2(m+6);s1[1]=a[0];for(int i=2;i<=n;i++){s1[i]=s1[i-1]+a[i-1];}s2[1]=b[0];for(int i=2;i<=m;i++){s2[i]=s2[i-1]+b[i-1];}while(q--){int x,y,z,ans=0;cin>>x>>y>>z;int l=max(0ll,z-y),r=min(x,z),mid1,mid2;l=max(l,z-m);r=min(r,z);r=min(r,n);while(r-l>=5){mid1=(l+l+r)/3;mid2=(l+r+r)/3;if(s1[mid1]+s2[z-mid1]<s1[mid2]+s2[z-mid2]){l=mid1;}else{r=mid2;}}for(int i=l;i<=r;i++){if(i<=n&&z-i<=m){ans=max(ans,s1[i]+s2[z-i]);}}cout<<ans<<'\n';}}return 0;
}

F 题，据说很简单，但还没写出代码，这里先挖个坑。