Transformer之多头注意力机制和位置编码(二)
Transformer之多头注意力机制和位置编码(二)
文章目录
- Transformer之多头注意力机制和位置编码(二)
- 一、 多头注意力(Multi-Head Attention)
- 案例
- 二、位置编码(Positional Encoding)
- 2.1 固定正弦/余弦
- 2.2 可学习编码
一、 多头注意力(Multi-Head Attention)
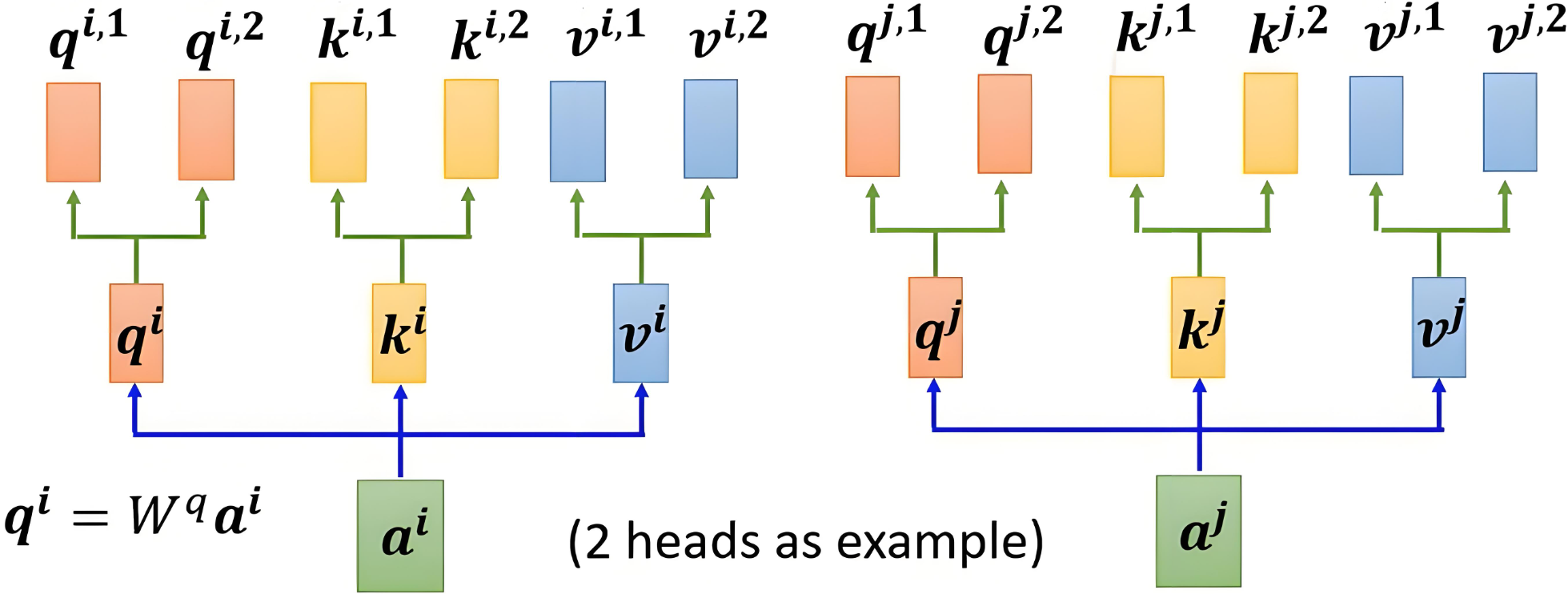 |
|---|
| 先把整句映射成 Q、K、V,再按列切分 → 多头并行计算 |
核心公式
headh=Attention(QWhQ,KWhK,VWhV)MultiHead(Q,K,V)=[head1;…;headH]WO\begin{aligned} \mathrm{head}_h &= \mathrm{Attention}(Q W^Q_h,\,K W^K_h,\,V W^V_h) \\[2pt] \mathrm{MultiHead}(Q,K,V) &= [\mathrm{head}_1;\dots;\mathrm{head}_H]W^O \end{aligned} headhMultiHead(Q,K,V)=Attention(QWhQ,KWhK,VWhV)=[head1;…;headH]WO
步骤速览
- 分头映射(
dim=512, head_num=8→ 每头d_k=64)head_num, d_k = 8, dim // 8 W_Q = nn.Linear(dim, dim) Q_h = W_Q(x).view(b, seq, head_num, d_k).transpose(1, 2) # [b, 8, seq, 64] # K_h, V_h 同理 - 并行注意力(缩放点积 + softmax)
- 拼接 + 线性
out = out.transpose(1, 2).contiguous().view(b, seq, dim) out = nn.Linear(dim, dim)(out) # 最终输出 [b, seq, 512]
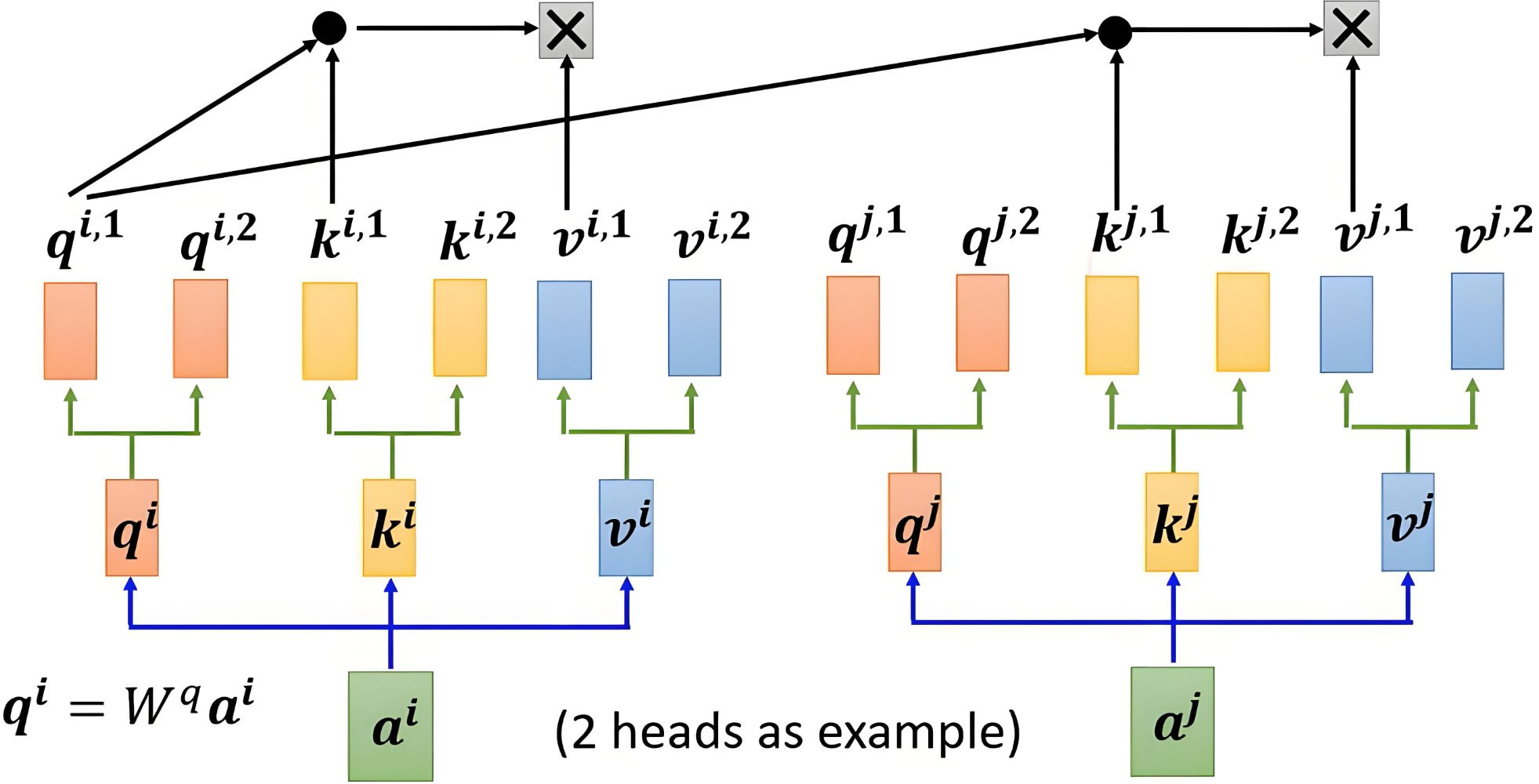 |
|---|
| 2 个头 = 2 组独立 (Q,K,V) 子空间 |
表达能力
不同头关注不同模式(句法、语义、指代…),组合后更灵活。
案例
下面给出可直接复用的“多头注意力”最小实现。
特点
- 用
nn.Module封装,方便后续放进nn.Sequential或 Transformer; - 逐行中文注释,一眼看懂每一步在干什么;
- 输出维度与原句向量一致
[batch, seq_len, dim],后续可继续堆叠。
import math
import torch
import torch.nn as nn
import torch.nn.functional as Fclass MultiHeadAttention(nn.Module):"""简化版多头注意力dim : 模型总维度(你的例子里是 256)head_num : 头数(你的例子里是 16)输出形状 : [batch, seq_len, dim]"""def __init__(self, dim: int = 256, head_num: int = 16):super().__init__()# assert :“必须保证 dim 能被 head_num 整除,否则就报错。”assert dim % head_num == 0 self.dim = dimself.head_num = head_numself.d_k = dim // head_num # 每个头的维度# 3 个线性层一次性把 Q/K/V 投影出来(比 ModuleList 更简洁)self.W_q = nn.Linear(dim, dim)self.W_k = nn.Linear(dim, dim)self.W_v = nn.Linear(dim, dim)# 最后的输出线性变换self.W_o = nn.Linear(dim, dim)def forward(self, x):"""x : [batch, seq_len, dim]return : 与 x 形状相同"""batch, seq_len, _ = x.shape# 1) 线性投影 → [batch, seq_len, dim]Q = self.W_q(x)K = self.W_k(x)V = self.W_v(x)# 2) 拆成多头 → [batch, head_num, seq_len, d_k]def reshape(t):return t.view(batch, seq_len, self.head_num, self.d_k).transpose(1, 2)Q = reshape(Q) # [batch, head_num, seq_len, d_k]K = reshape(K)V = reshape(V)# 3) 缩放点积注意力scores = torch.matmul(Q, K.transpose(-2, -1)) / math.sqrt(self.d_k) # [B,h,seq,seq]attn = F.softmax(scores, dim=-1) # 归一化out = torch.matmul(attn, V) # [B,h,seq,d_k]# 4) 合并多头 → [batch, seq_len, dim]out = out.transpose(1, 2).contiguous().view(batch, seq_len, self.dim)# 5) 最后线性变换return self.W_o(out)# ------------------ 测试 ------------------
if __name__ == "__main__":sentences = ["i am an NLPer"]vocab = sorted({w for sent in sentences for w in sent.split()})word2idx = {w: i for i, w in enumerate(vocab)}indices = torch.tensor([[word2idx[w] for w in sent.split()] for sent in sentences])dim = 256embedding = nn.Embedding(len(vocab), dim)x = embedding(indices) # [1, 4, 256]mha = MultiHeadAttention(dim=256, head_num=16)y = mha(x) # [1, 4, 256]print("输入:", x.shape)print("输出:", y.shape)
运行结果
输入: torch.Size([1, 4, 256])
输出: torch.Size([1, 4, 256])
二、位置编码(Positional Encoding)
自注意力本身“无顺序”,需显式注入位置信号。
2.1 固定正弦/余弦
给定位置 i 与维度 2j / 2j+1:
PE(i,2j)=sin(i100002j/d)PE(i,2j+1)=cos(i100002j/d)\begin{aligned} PE(i,2j) &= \sin\!\left(\dfrac{i}{10000^{2j/d}}\right) \\[4pt] PE(i,2j+1) &= \cos\!\left(\dfrac{i}{10000^{2j/d}}\right) \end{aligned} PE(i,2j)PE(i,2j+1)=sin(100002j/di)=cos(100002j/di)
-
例子:句子
<BOS> 我 喜欢 自然语言 处理(N=5, d=512)
计算得到的 5×512 位置矩阵与词嵌入逐位相加即可。
说明: -
iii 是序列中位置的索引(从 000 开始)。
-
jjj 是词向量的维度索引(从 000 到 d/2−1d/2 - 1d/2−1)。
-
100001000010000 是一个超参数,用于控制频率的衰减。
 |
|---|
| 句子长度为 555,编码向量维数 D=4D=4D=4 |
- 外推特性:
已知 PE(pos)PE(pos)PE(pos) 可线性组合得到 PE(pos+k)PE(pos+k)PE(pos+k),模型可处理比训练集更长的句子。
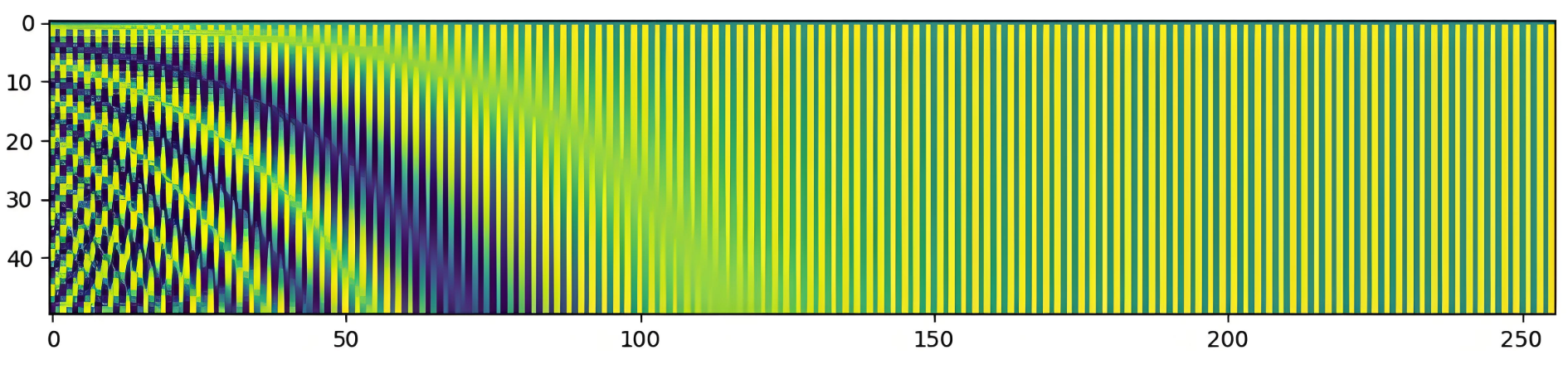 |
|---|
| 505050 个词嵌入,维度 512512512 的位置编码热力图 |
2.2 可学习编码
直接把位置当 token 训,表现好但依赖最大长度超参。
小结
多头 = “多组独立子空间”并行注意力;
位置编码 = “给并行计算加上顺序感”。二者配合让 Transformer 既能并行又能保持序列有序。
