算法题打卡力扣第11题:盛最多水的容器(mid)
题目描述
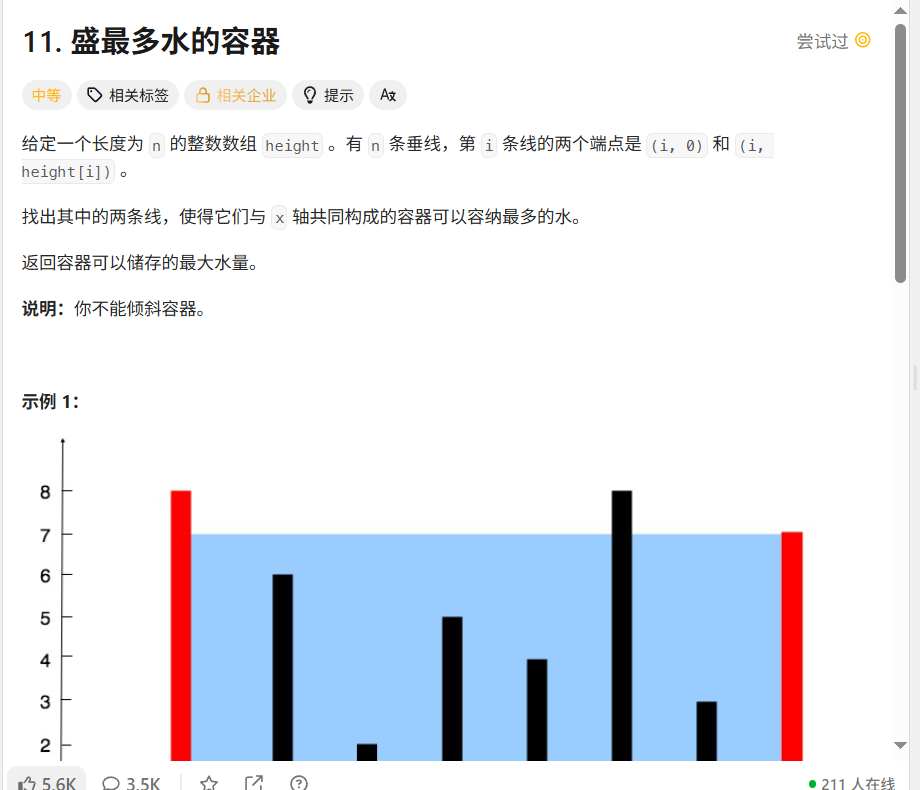
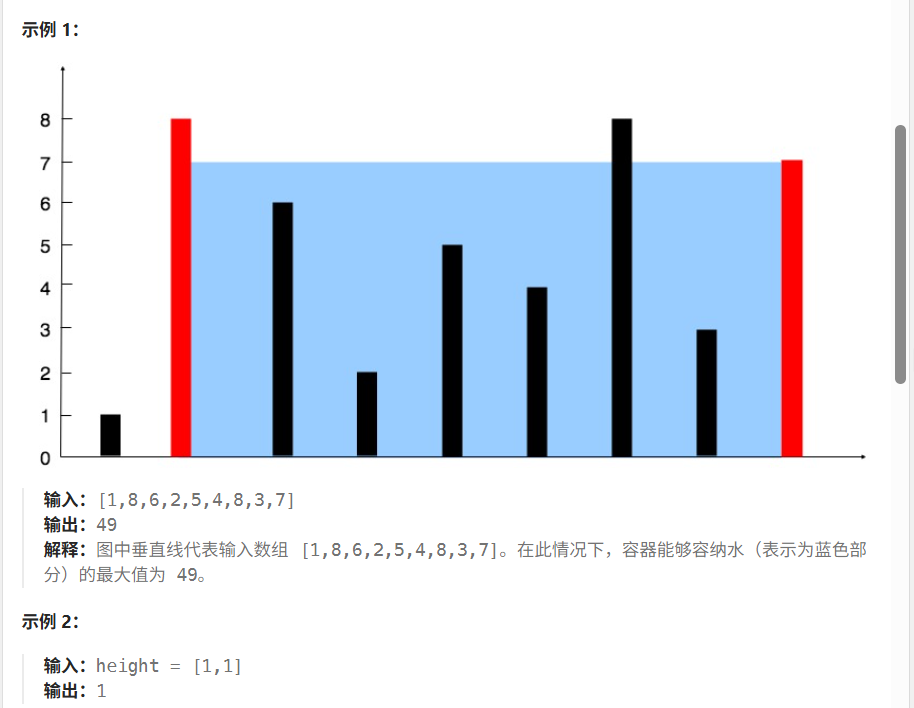
提示:
n == height.length
2 <= n <= 105
0 <= height[i] <= 104
解法一 (暴力解)
首先我的想法是暴力解,依次计算每一个可能的面积大小,然后比较得出最大的面积。
选定一条左边的线 i。
再选定一条右边的线 j。
计算这两条线组成的容器面积:面积 = (j - i) * min(height[i], height[j])。
用两层 for 循环来遍历所有 (i, j) 的组合,不断更新最大面积。
代码如下:
class Solution {
public:int maxArea(vector<int>& height) {int i,j,area=0,max=0;for(i=0;i<height.size();i++){for(j=height.size()-1;j>i;j--){area=(j-i)*min(height[i],height[j]);if(area>max){max=area;}}}return max;}
};
结果:
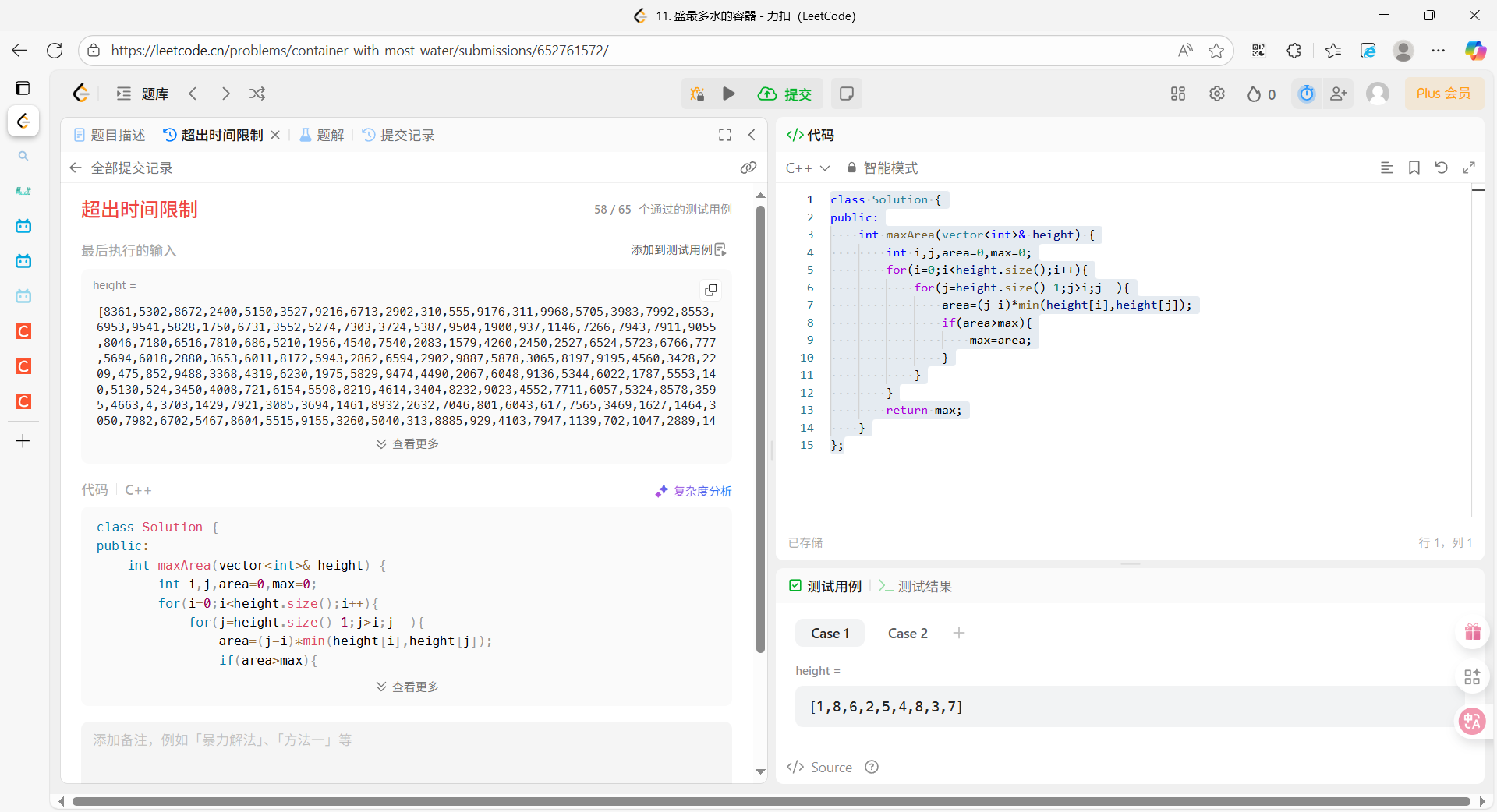
显示超出时间限制,让我们来分析一下时间复杂度,两个for循环,1+2+3+n-1=n(1+n-1)/2,所以时间复杂度是O(n^2),空间复杂度是O(1)
解法二 (双指针 from gimini老师)
既然暴力法太慢,我们就要想办法减少不必要的计算。双指针法的精髓就在于每一步都排除掉不可能产生更优解的选项。
1.从哪里开始?
要想让面积最大,面积 = 宽度 × 高度,我们希望宽度和高度都尽可能大。
- 宽度 最大的情况是什么?当然是选择数组最两端的两条线。
- 所以,我们可以从这里入手:一个指针 left 指向数组开头,一个指针 right 指向数组末尾。这是我们的初始状态,拥有了最大可能的宽度。
- 下一步怎么走?(核心决策)
现在我们有了一个初始的容器(可能是最大的,也可能不是)。接下来,我们需要移动一个指针,让宽度变窄,来探索有没有可能找到更高的容器,从而获得更大的总面积。
关键问题: 我们应该移动 left 指针还是 right 指针?
让我们来分析一下:
- 当前容器的面积是 (right - left) * min(height[left], height[right])。
- 容器的储水量由较短的那块木板决定(木桶效应)。
假设 height[left] 比 height[right] 短。
- 如果我们移动右指针 right 向左,新的宽度肯定变小了,而容器的新高度仍然受限于 height[left] (因为新的右板即使再高,短板还是 height[left])。所以,面积必然会变小。移动长板对于当前情况来说,没有任何益处。
- 反之,如果我们移动左指针 left 向右,虽然宽度也变小了,但我们给了自己一个寻找更高左板的机会。如果新的 height[left] 变得更高,就有可能弥补宽度减小的损失,从而得到一个更大的面积。
结论:
在每一步,我们都应该移动指向较短木板的那个指针。这是整个算法最核心的贪心思想。
算法流程总结
- 初始化:
左指针 left = 0。
右指针 right = height.length - 1。
最大面积 maxArea = 0。
- 循环:只要 left < right,就不断重复以下步骤:
计算当前宽度 width = right - left。
找出较短的板高 h = min(height[left], height[right])。
计算当前面积 currentArea = width * h。
更新历史最大面积 maxArea = max(maxArea, currentArea)。
移动指针:
如果 height[left] < height[right],则 left++。
否则,right–。
- 结束:当 left 和 right 相遇,说明所有可能性都已探索完毕,返回 maxArea。
完整代码如下:
class Solution {
public:int maxArea(vector<int>& height) {int left=0,right = height.size() - 1,maxArea = 0;int width=0,currentArea=0,h=0;while(left < right){width = right - left;h = std::min(height[left],height[right]);currentArea = width * h;maxArea = std::max(maxArea,currentArea);if(height[left]<height[right]){left++;}else{right--;}}return maxArea;}
};
运行结果如下:
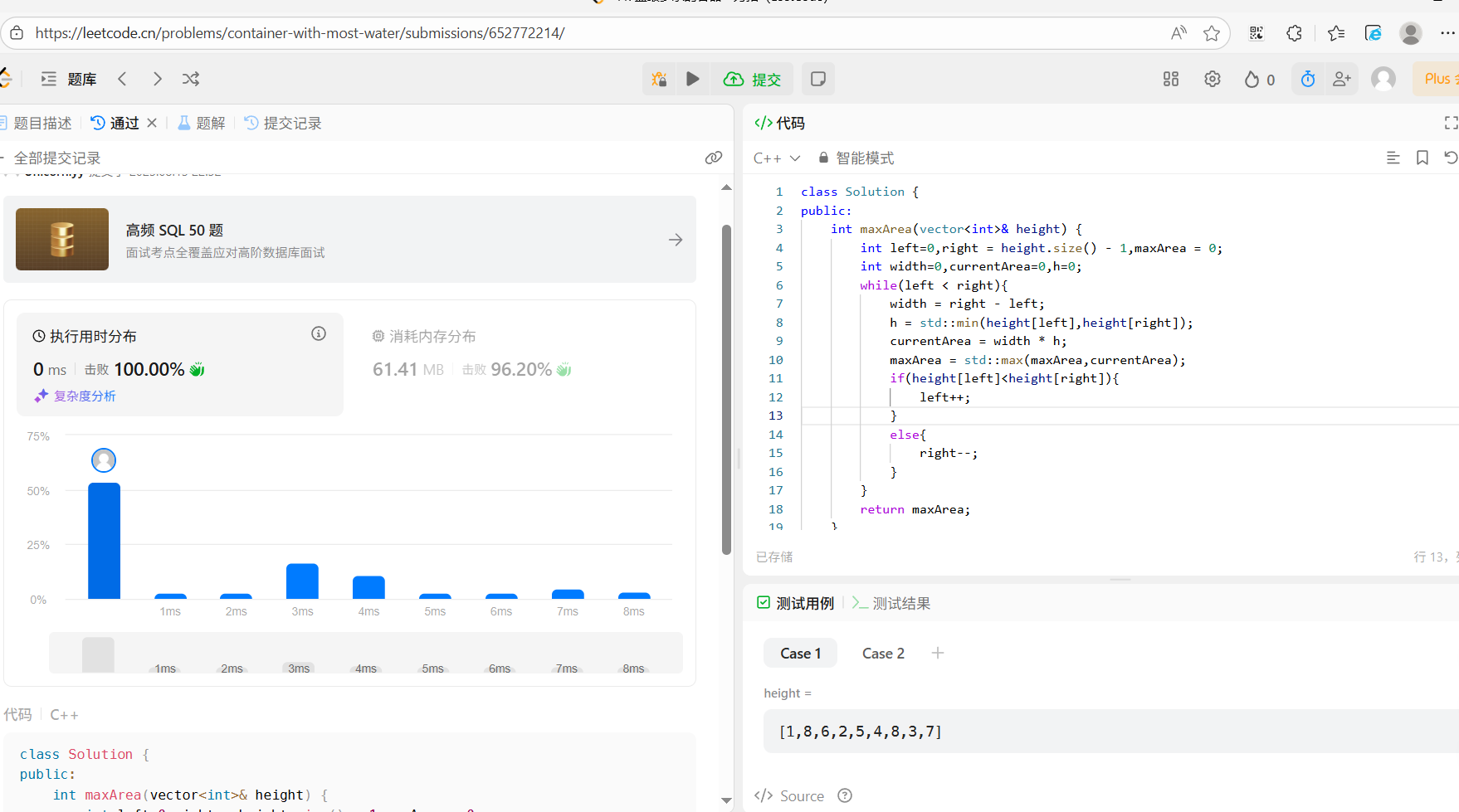
时间复杂度分析:
只使用了一个for循环,时间复杂度为O(n)
空间复杂度为O(1)
ok,双指针太好用了!!!
如果还有不懂的小伙伴可以看看这个视频讲的不错~
盛最多水的容器 接雨水
ok,see you next time!
