当前位置：首页 > news >正文

机器学习-Cluster

news 2025/8/14 11:21:52

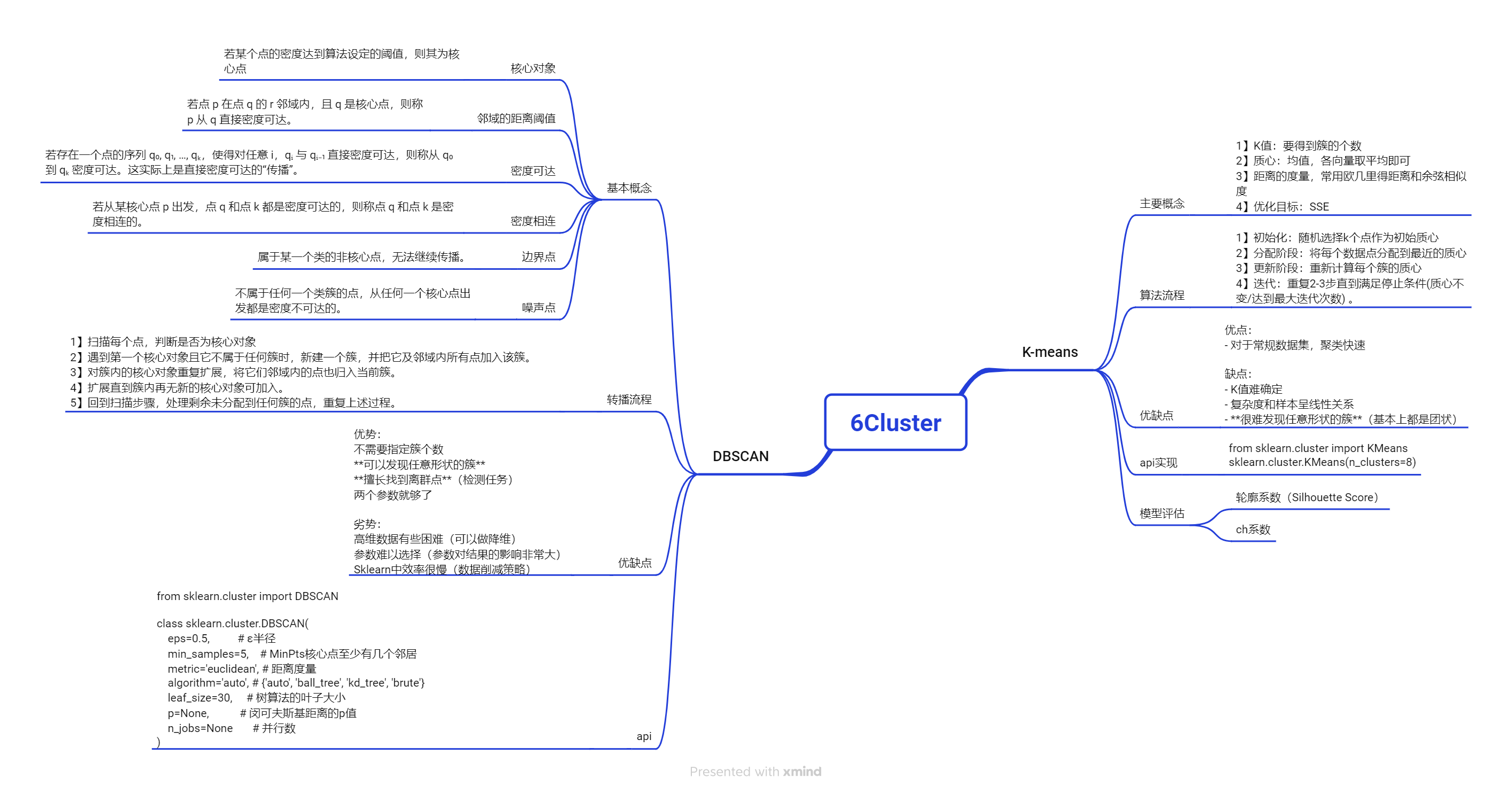
在这里插入图片描述

0 客户细分

from sklearn.cluster import KMeans,DBSCAN
from sklearn.metrics import silhouette_score
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
from sklearn.feature_extraction import DictVectorizer
from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_score
from sklearn.preprocessing import StandardScaler
import warnings
warnings.filterwarnings("ignore", category=UserWarning, module="sklearn.cluster._kmeans")# 忽略不必要的警告plt.rcParams['font.sans-serif'] = ['KaiTi']  # 使用黑体
plt.rcParams['axes.unicode_minus'] = False  # 解决负号显示问题# 封装一个函数用于可视化聚类效果
def visualization(data,c=None,title=None):plt.scatter(data.iloc[:, 0], data.iloc[:,1],c=c)plt.title(title)plt.show()
data = pd.read_csv('../data/Mall_Customers.csv')# 独热编码
dummy = pd.get_dummies(data["Gender"],dtype=int)
data = pd.concat([data, dummy], axis=1)
data.drop(['Gender'], axis=1, inplace=True)# 基于可视化结果发现二维的分类效果最明显，选择降到二维
pca = PCA(n_components=2)
data = pca.fit_transform(data)
data = pd.DataFrame(data,columns=['x','y'])# 初步可视化看看数据什么样子
data1=data.copy()  # 深拷贝一个对象data1，不影响data，data1用于初步观察数据
visualization(data1,title="聚类前")
# 基于sc结合初步可视化判断k值
sc = []
rank_k = range(2,7)
for k in rank_k:kmeans = KMeans(n_clusters=k)labels = kmeans.fit_predict(data)sc.append(silhouette_score(data,labels))print(k,silhouette_score(data,labels))# 实例化
kmeans = KMeans(n_clusters=5)
dbscan = DBSCAN(eps=15, min_samples=8)# 获取聚类结果
dbscan_labels = dbscan.fit_predict(data)
kmeans_labels = kmeans.fit_predict(data)
# centers = kmeans.cluster_centers_# 可视化，根据聚类结果着色
visualization(data,c=kmeans_labels,title="kmeans聚类后")
#由于数据是"团状:的，dbscan结果明显不如k-means
visualization(data,c=dbscan_labels,title="dbscan聚类后")

结果
在这里插入图片描述

聚类算法

（聚类不是分类，分类是有监督学习。聚类任务在完成之前之前都没有类的概念，只是纯粹的数据，聚类常作为是在分类之前的任务(因为聚类完成后有了类别就可以开始分类了)）

1 K-means

1.1算法本质和数学公式

1】K值：要得到簇的个数
2】质心：均值，各向量取平均即可
3】距离的度量，常用欧几里得距离和余弦相似度
4】优化目标 $KaTeX parse error: Double subscript at position 30: …{K}\sum_{x\in_C_̲i}dist(c_i,x)^2$ （这个公式叫SSE(误差平方和)，最小化每个簇的每个x到其对应质心距离的和）

1.2 算法流程

1】初始化‌：随机选择k个点作为初始质心（目前最常用的k-means++，一般第一个质心完全随机选择，第二个质心开始会加上距离权重偏向于选择远的地方作为质心，并不是完全随机）

2】分配阶段‌：将每个数据点分配到最近的质心（计算每个数据点到各个质心的距离，最后分到最近的那个质心对应的簇）

3】更新阶段‌：重新计算每个簇的质心(均值点，每个维度相加取均值，比如平面上聚类,质心的x就取簇内每个点的x轴的值相加取平均，计算y同计算x)

4】迭代‌：重复2-3步直到满足停止条件(质心不变/达到最大迭代次数) 。(在sklearn的算法中每轮迭代都会计算SSE（ $SSE=∑i=1K∑x∈Ci∥x−ci∥2\mathrm{SSE} = \sum_{i=1}^{K} \sum_{x \in C_i} \|x - c_i\|^2$ )）SSE就作为本轮的损失，是否继续迭代也取决于SSE

1.3 优缺点

优点：

对于常规数据集，聚类快速

缺点：

K值难确定
复杂度和样本呈线性关系
很难发现任意形状的簇（基本上都是团状）

1.4 api

from sklearn.cluster import KMeans

sklearn.cluster.KMeans(n_clusters=8)

参数:
n_clusters:开始的聚类中⼼数量，整型，缺省值=8，⽣成的聚类数，即产⽣的质⼼（centroids）数。

⽅法:
estimator.fit(x) # 模型训练
estimator.predict(x) # 预测值
estimator.fit_predict(x) #前两种功能结合
（计算聚类中⼼并预测每个样本属于哪个类别,相当于先调⽤fit(x) 然后再调⽤predict(x)）

kmeans代码示例

from sklearn.cluster import KMeans
from sklearn.datasets import make_blobs # make_blobs生成模拟数据
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['KaiTi']  # 使用黑体
plt.rcParams['axes.unicode_minus'] = False  # 解决负号显示问题# 第一种生成方式，指定簇的数量和标准差，簇的位置随机且标准差统一
X, _ = make_blobs(  # _表示y，这里用不到就用_表示n_samples=300, # 表示样本数n_features=2,# n_features表示有几列,centers=4, # centers表示簇的数量cluster_std=1,  # 簇的标准差    
) 
# 第二种生成方式，自己控制center的位置并独立控制每个簇的标准差
X1,_ = make_blobs(n_samples=1000, #样本量n_features=2,  # 维度centers=[[-1,-1],[0,0],[1,1],[2,2]],  # 设置四个簇的中心点cluster_std=[[0.05],[0.1],[0.2],[0.3]],  # 为每个簇独立设置标准差random_state=42
)
plt.figure(figsize=(10,8))
plt.scatter(X1[:,0], X1[:,1],s=30)
plt.show()kmeans = KMeans(n_clusters=4,)
kmeans.fit(X)
labels  = kmeans.predict(X) #  # labels表示对每个点的聚类结果
centers = kmeans.cluster_centers_ # 获取各个质心的坐标
print(centers)plt.figure(figsize=(10,8))
plt.scatter(X[:,0], X[:,1],c=labels,s=30)
plt.scatter(centers[:,0], centers[:,1],marker='o',c="red",s=100)  # 绘制各簇中心点，s表示size 大小
plt.show()

结果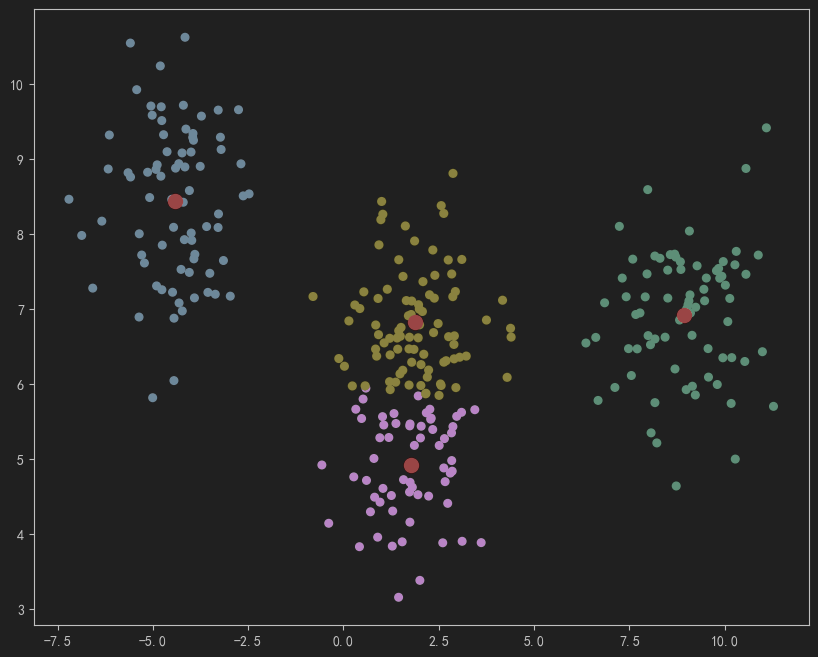

1.5 模型评估

1.5.1 轮廓系数（一般不用于DBSCAN）

轮廓系数（Silhouette Score）是一个衡量聚类质量的指标，其值范围为 [-1, 1]：
值越接近 1：表示样本被正确地聚类到了自己的簇中，且与其他簇之间的距离较远，聚类效果很好。
值接近 0：表示样本位于两个簇的边界上，难以归类，聚类效果一般。
值接近 -1：表示样本可能被错误地聚类到了错误的簇中，聚类效果较差。
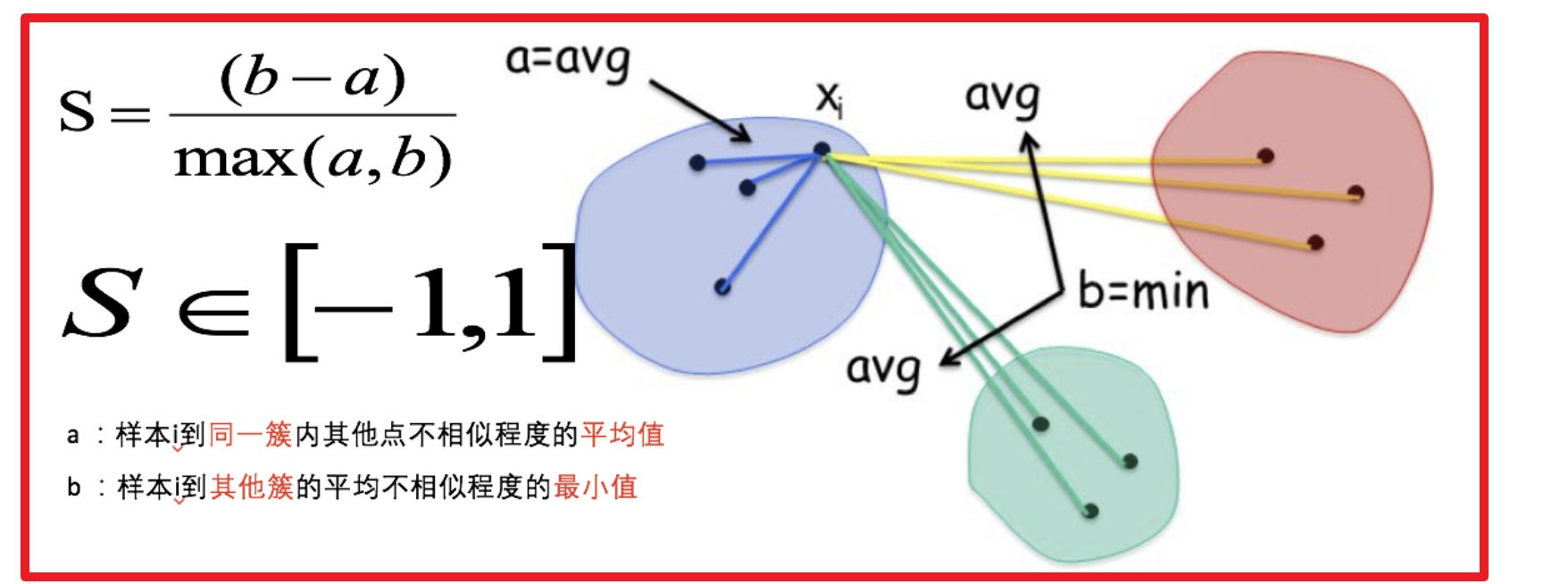
在这里插入图片描述

1.5.2 轮廓系数确定K值

代码示例

sc = []  # 由于存储不同k值对应的sc系数
range_k = range(2,11)
for k in range_k:kmeans = KMeans(n_clusters=k,random_state=42)labels = kmeans.fit_predict(X)  #训练并预测的标签，只是合并两个操作score = silhouette_score(X,labels)sc.append(score)
plt.figure(figsize=(10,8))
plt.plot(range_k,sc)
plt.grid()
plt.show()  # 最后k的最优为3

1.5.3 轮廓系数优缺点*

优点：

直观解释‌：得分范围明确，易于理解
无需基准标签‌：适用于无监督学习评估
考虑聚类形状‌：比简单的距离指标更全面

缺点：

计算成本较高‌：需要计算所有样本对的距离
偏向凸形簇‌：与K-Means有相同局限
对密度变化敏感‌：不同密度的簇可能影响评估

1.5.4 与其他评估指标对比

指标名称	需要真实标签	适合的聚类场景/特点	计算复杂度
轮廓系数	否	各类簇大小相近时表现最佳	O(n²)
卡林斯基-哈拉巴斯指数	否	各类簇大小差异大时更好	O(n)
戴维森-博尔丁指数	否	任意形状簇	O(n²)
调整兰德指数	是	有基准标签时最准确	O(n²)

1.6 根据SSE的肘部法则确定k值

（该方法相较通过sc的方法适用面更广，效果不一定）

肘部法则代码示例

# k太大会失去意义，只保留能让sse能大幅下降时的最大k
sse_values = []for k in range(1, 10):kmeans = KMeans(n_clusters=k, random_state=42)kmeans.fit(X)sse_values.append(kmeans.inertia_)  # 簇内误差平方和# 绘制肘部曲线
plt.plot(range(1,10), sse_values, 'o-')
plt.xlabel('聚类数 k')
plt.ylabel('SSE')
plt.title('不同k下的SSE')
plt.show()
## 选择“肘部”的k值就行

1.7 根据CH系数确定k值

（这个并不是很好用，且一般也不用于dbscan）

CH系数： $CH=簇间离散度簇内离散度=trace(B)/(K−1)trace(W)/(n−K)\mathrm{CH} = \frac{\text{簇间离散度}}{\text{簇内离散度}} = \frac{\mathrm{trace}(B)/(K-1)}{\mathrm{trace}(W)/(n-K)}$
（trace表示迹）
ch系数代码示例

import numpy as np
from sklearn.metrics import calinski_harabasz_scorech_scores = []for k in range(2,10):  # CH系数要求k>=2kmeans = KMeans(n_clusters=k, random_state=42)labels = kmeans.fit_predict(X)# 计算CH系数ch_score = calinski_harabasz_score(X, labels)ch_scores.append(ch_score)# 绘制CH系数曲线
plt.plot(range(2, 10), ch_scores, 'o-')
plt.xlabel('聚类数 k')
plt.ylabel('CH系数')
plt.title('CH系数法确定最优k')# 找到CH系数的局部最大值对应的k（也有类似于肘部法则的思想，不能完全取ch最大的k，这里选的k=4最合理，4-5提升小，5-6提升极大很可能已经过拟合）
optimal_k = range(2, 10)[np.argmax(ch_scores)]

2 DBSCAN

2.1 基本概念

核心对象：若某个点的密度达到算法设定的阈值，则其为核心点（即在半径 r 的邻域内点的数量 ≥ minPts）。
$∈\in$ -邻域的距离阈值：设定的半径 r。
直接密度可达：若点 p 在点 q 的 r 邻域内，且 q 是核心点，则称 p 从 q 直接密度可达。
密度可达：若存在一个点的序列 q₀, q₁, …, qₖ，使得对任意 i，qᵢ 与 qᵢ₋₁ 直接密度可达，则称从 q₀ 到 qₖ 密度可达。这实际上是直接密度可达的“传播”。
密度相连：若从某核心点 p 出发，点 q 和点 k 都是密度可达的，则称点 q 和点 k 是密度相连的。
边界点：属于某一个类的非核心点，不能发展下线了。
噪声点：不属于任何一个类簇的点，从任何一个核心点出发都是密度不可达的。

2.2 传播流程

1】扫描每个点，判断是否为核心对象（根据 eps 和 min_samples 判定）。
2】遇到第一个核心对象且它不属于任何簇时，新建一个簇，并把它及邻域内所有点加入该簇。
3】对簇内的核心对象重复扩展，将它们邻域内的点也归入当前簇。
4】扩展直到簇内再无新的核心对象可加入。
5】回到扫描步骤，处理剩余未分配到任何簇的点，重复上述过程。

2.3 dbcan优缺点

优势：
不需要指定簇个数
可以发现任意形状的簇
擅长找到离群点（检测任务）
两个参数就够了

劣势：
高维数据有些困难（可以做降维）
参数难以选择（参数对结果的影响非常大）
Sklearn中效率很慢（数据削减策略）

2.4 api 介绍

from sklearn.cluster import DBSCAN

class sklearn.cluster.DBSCAN(
eps=0.5, # ε半径
min_samples=5, # MinPts核心点至少有几个邻居
metric=‘euclidean’, # 距离度量
algorithm=‘auto’, # {‘auto’, ‘ball_tree’, ‘kd_tree’, ‘brute’}
leaf_size=30, # 树算法的叶子大小
p=None, # 闵可夫斯基距离的p值
n_jobs=None # 并行数
)

重要属性
dbscan.core_sample_indices_ # 核心点索引数组
dbscan.components_ # 核心点坐标数组
dbscan.labels_ # 每个点的簇标签(-1表示噪声)

2.5 模型评估*

大多数情况直接降维可视化看效果。或者检查噪声多不多

ARI（调整兰德指数）、NMI（归一化互信息）等。
仅在有真实标签的情况下使用，能客观量化聚类质量。

DBSCAN代码示例

from sklearn.cluster import DBSCAN
from sklearn.datasets import make_moonsX,_ = make_moons(n_samples=500,noise=0.05, #标准差
)
dbscan = DBSCAN(eps=0.2 , # 指定领域半径min_samples=5, # 核心对象为中点在eps半径内至少有五个点（包括核心对象）
)labels = dbscan.fit_predict(X)plt.figure(figsize=(10,8))
plt.scatter(X[:,0], X[:,1],c=labels)
plt.show()