数据结构 二叉树(2)堆
这里写目录标题
- 堆的概念与性质解析
- 1. 堆的定义
- 2. 堆的核心性质
- 3. 堆与普通完全二叉树的区别
- 1.3 堆的实现
- 1.3.1 堆向下调整算法
- 1.3.2 堆的创建
- 3.2.3 建堆时间复杂度
- 3.2.4 堆的插入
- 3.2.5 堆的删除
- 3.2.6 堆的代码实现
- 一、代码功能模块梳理
- 二、关键函数解析
- 1. 交换函数 Swap
- 2. 向下调整 `AdjustDown`(小堆 )
- 3. 堆初始化 `HeapInit`
- 4. 堆销毁 `HeapDestory`
- 5. 向上调整 `AdjustUp`(小堆 )
- 6. 堆插入 `HeapPush`
- 7. 堆删除 `HeapPop`(删除堆顶 )
- 8. 堆顶获取 `HeapTop`
- 9. 判空与 size 获取
- 4. 堆的实际运用 - 堆排序
- 4.1 堆排序核心原理
- 4.2 升序排序 - 建大堆的必要性
- 4.3 堆排序完整流程(升序 - 大堆实现 )
- 4.4 堆排序的时间与空间复杂度
- 4.5 TOP-K 问题
- 4.5.1 问题定义与核心痛点
- 4.5.2 堆解法核心思路
- 4.5.3 示例:求前 3 个最大元素
- 4.5.4 代码实现:PrintTopK 函数
- 4.5.5 堆解法的优势与适用场景
堆的概念与性质解析
1. 堆的定义
核心逻辑:
堆是完全二叉树的顺序存储优化,需同时满足“完全二叉树结构”和“父子节点值的约束关系”。
数学描述(以数组下标 i 对应完全二叉树节点为例 ):
-
对于小根堆(最小堆):任意节点
k[i]需满足k [i] ≤ k [2i+1](左孩子) 且 k [i] ≤ k [2i+2](右孩子)即父节点值 ≤ 左右子节点值,根节点是整个堆的最小值。 -
对于大根堆(最大堆):任意节点
k[i]需满足k [i] ≥ k [2i+1](左孩子) 且 k [i] ≥ k [2i+2](右孩子)即父节点值 ≥ 左右子节点值,根节点是整个堆的最大值。
示例(结合小根堆/大根堆图示 ):
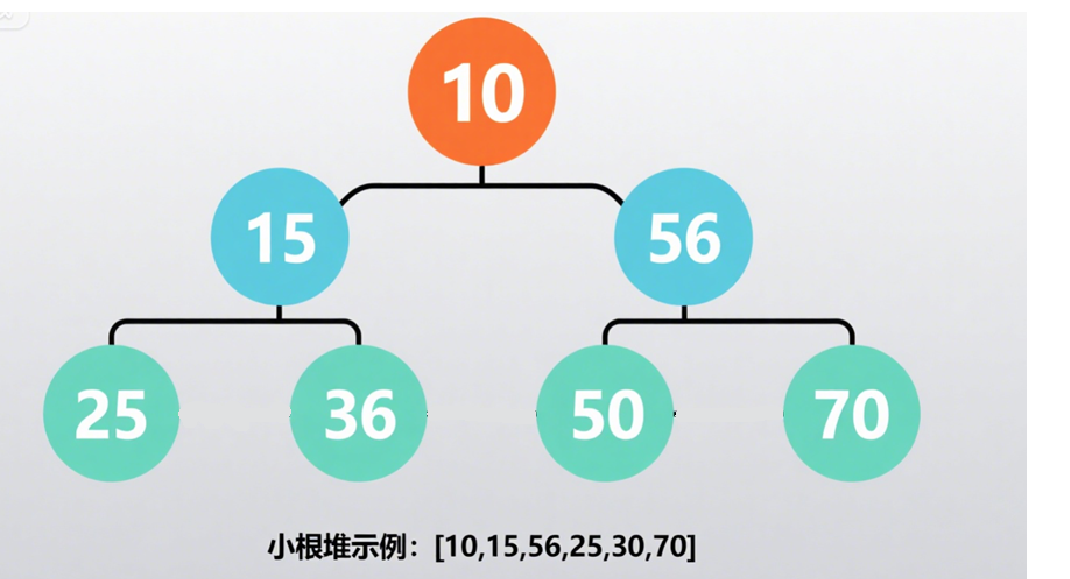
-
小根堆示例(数组
[10,15,56,25,30,70]):
根节点10(下标 0 ),左孩子15(下标 1 )、右孩子56(下标 2 )→10 ≤ 15且10 ≤ 56✔️;
节点15(下标 1 ),左孩子25(下标 3 )、右孩子30(下标 4 )→15 ≤ 25且15 ≤ 30✔️;
符合小根堆“父≤子” 规则。 -
大根堆示例(数组
[70,56,30,25,15,10]): -
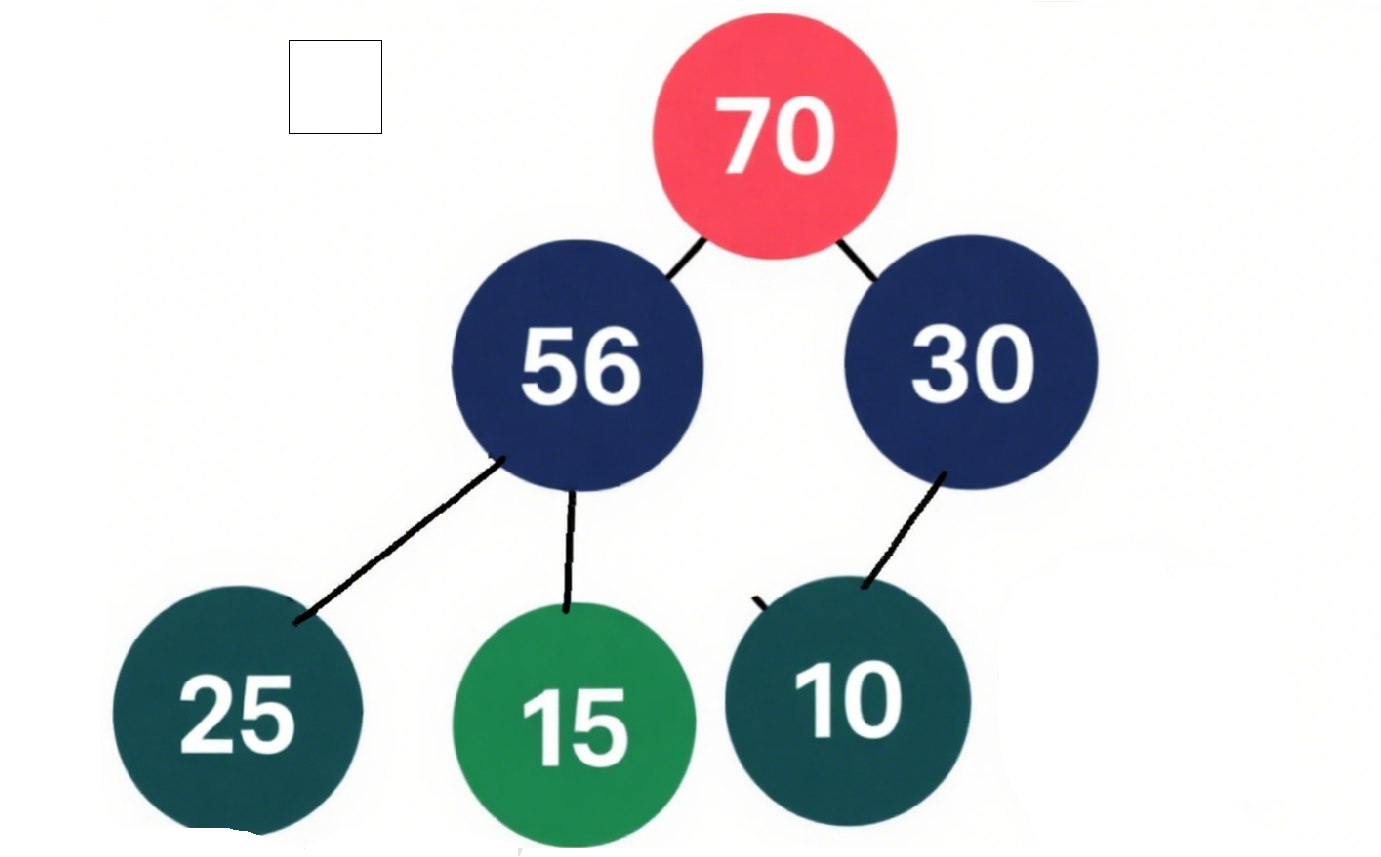
根节点 70(下标 0 ),左孩子 56(下标 1 )、右孩子 30(下标 2 )→ 70 ≥ 56 且 70 ≥ 30 ✔️;
节点 56(下标 1 ),左孩子 25(下标 3 )、右孩子 15(下标 4 )→ 56 ≥ 25 且 56 ≥ 15 ✔️;
符合大根堆“父≥子” 规则。
2. 堆的核心性质
性质 1:结构特性
堆必须是完全二叉树,节点按“从上到下、从左到右”的层序存储在数组中,不允许中间出现“空缺节点”(否则无法用简单的 2i+1/2i+2 公式关联父子 )。
示例验证:
小根堆的存储结构 [10,15,56,25,30,70] 对应完全二叉树,每一层节点连续无空缺;若数组为 [10,15,_,25](_ 表示空缺 ),则不满足完全二叉树,无法构成堆。
性质 2:值的约束特性
- 小根堆:父节点是子树的最小值(根节点是全局最小值 )。
- 大根堆:父节点是子树的最大值(根节点是全局最大值 )。
示例验证:
大根堆中,节点 70(下标 0 )是根,其左子树(56、25、15 )和右子树(30、10 )的所有节点值均 ≤ 70 ✔️;
节点 56(下标 1 )是左子树的根,其左孩子 25、右孩子 15 均 ≤ 56 ✔️。
性质 3:操作高效性
堆的核心操作(插入、删除堆顶 )基于“向下调整”或“向上调整”,时间复杂度为 O(log n)(n 是节点数 ),利用完全二叉树的高度为 log n 特性,保证高效性。
示例说明:
对含 6 个节点的堆(高度 3 ),插入/删除操作最多只需调整 3 层(从叶子到根或根到叶子 ),远快于普通数组的 O(n) 操作。
3. 堆与普通完全二叉树的区别
核心差异:普通完全二叉树无值的约束,仅要求结构连续;堆额外要求父子节点值的大小关系(小根堆父≤子,大根堆父≥子 )。
示例对比:
- 普通完全二叉树数组:
[10,56,15,25,30,70](结构连续,但10 < 56不满足大根堆“父≥子” )。 - 大根堆数组:
[70,56,30,25,15,10](结构连续 + 父≥子 )。
结论:堆是“有值约束的完全二叉树”,结构 + 值规则缺一不可。
1.3 堆的实现
1.3.1 堆向下调整算法
核心逻辑:
在左右子树已满足堆性质的前提下,从根节点开始,将当前节点与左右子节点中符合堆规则(小堆选更小、大堆选更大 )的节点交换,逐层向下调整,使整棵树满足堆性质。
前提条件:
左右子树必须已是堆(小堆/大堆 ),否则调整无法保证结果正确。
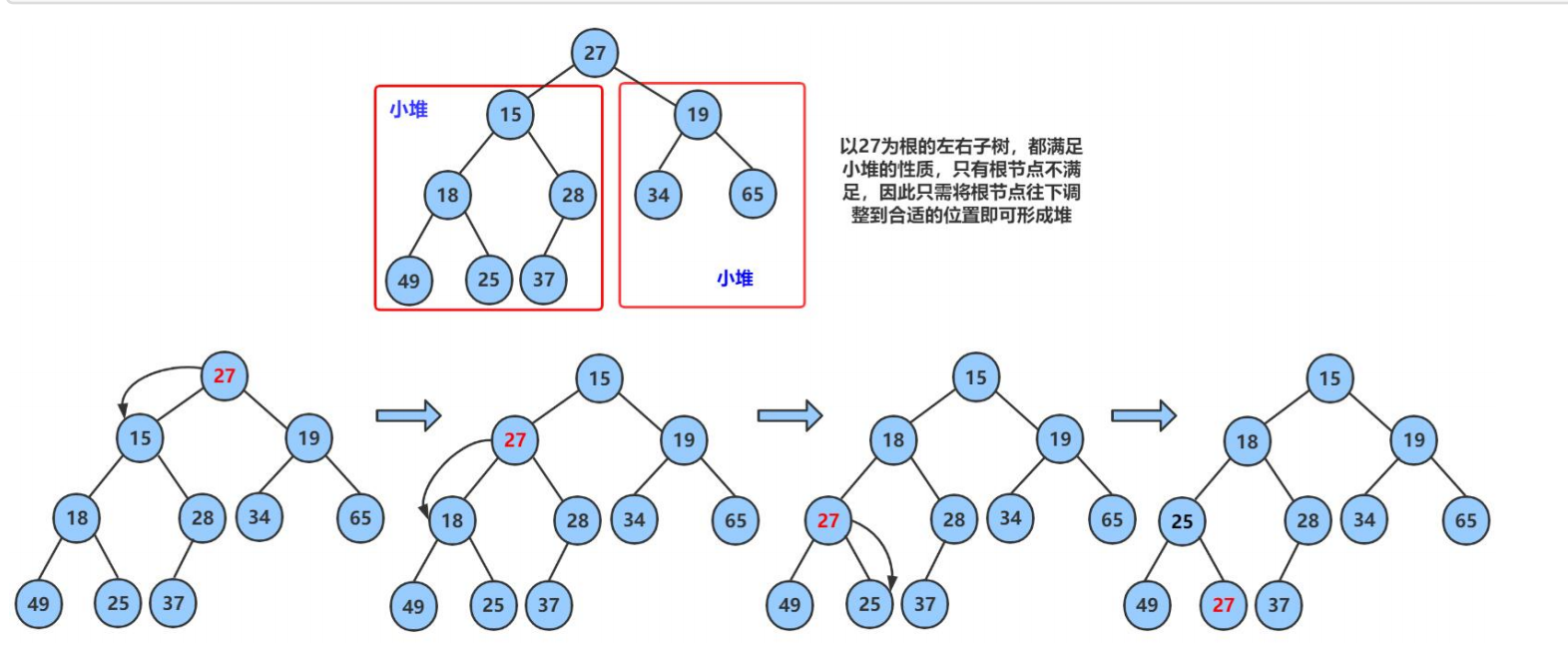
算法步骤(以小堆调整为例,数组 array[] = {27,15,19,18,28,34,65,49,25,37} ):
- 定位根节点与子节点:
根节点下标i = 0(值27),左子节点下标2i+1 = 1(值15),右子节点下标2i+2 = 2(值19)。 - 选择调整目标:
小堆需父节点 ≤ 子节点,比较左右子节点,选更小的(15)与父节点比较。 - 交换与递归调整:
因27 > 15,交换根节点与左子节点 → 数组变为{15,27,19,18,28,34,65,49,25,37}。
交换后,原根节点(27)移动到下标1,需继续调整其左右子树(下标3、4,值18、28):- 比较
27与18(左子节点更小 ),因27 > 18,再次交换 → 数组变为{15,18,19,27,28,34,65,49,25,37}。 - 交换后,
27移动到下标3,其左右子节点下标7、8(值49、25),因27 < 49且27 < 25不成立(27 > 25),继续交换27与25→ 数组变为{15,18,19,25,28,34,65,49,27,37}。 - 交换后,
27移动到下标8,无有效子节点,调整结束。
代码实现(C 语言,小堆向下调整 ):
- 比较
void AdjustDown(int* a, int n, int parent) {int child = 2 * parent + 1; // 先默认左孩子while (child < n) {// 选左右孩子中更小的(小堆)if (child + 1 < n && a[child + 1] < a[child]) {child++;}// 孩子比父小,交换并继续调整if (a[child] < a[parent]) {swap(&a[child], &a[parent]);parent = child;child = 2 * parent + 1;} else {break; // 满足堆性质,结束调整}}
}
示例验证:
初始数组经调整后,满足小堆性质(父节点 ≤ 左右子节点 ),如根节点 15 ≤ 18 且 15 ≤ 19 ,下标 1 的 18 ≤ 25 且 18 ≤ 28 等。
1.3.2 堆的创建
核心逻辑:
若根节点左右子树不是堆,需从倒数第一个非叶子节点开始,从下往上、从右往左依次调整每棵子树,最终使整棵树满足堆性质。
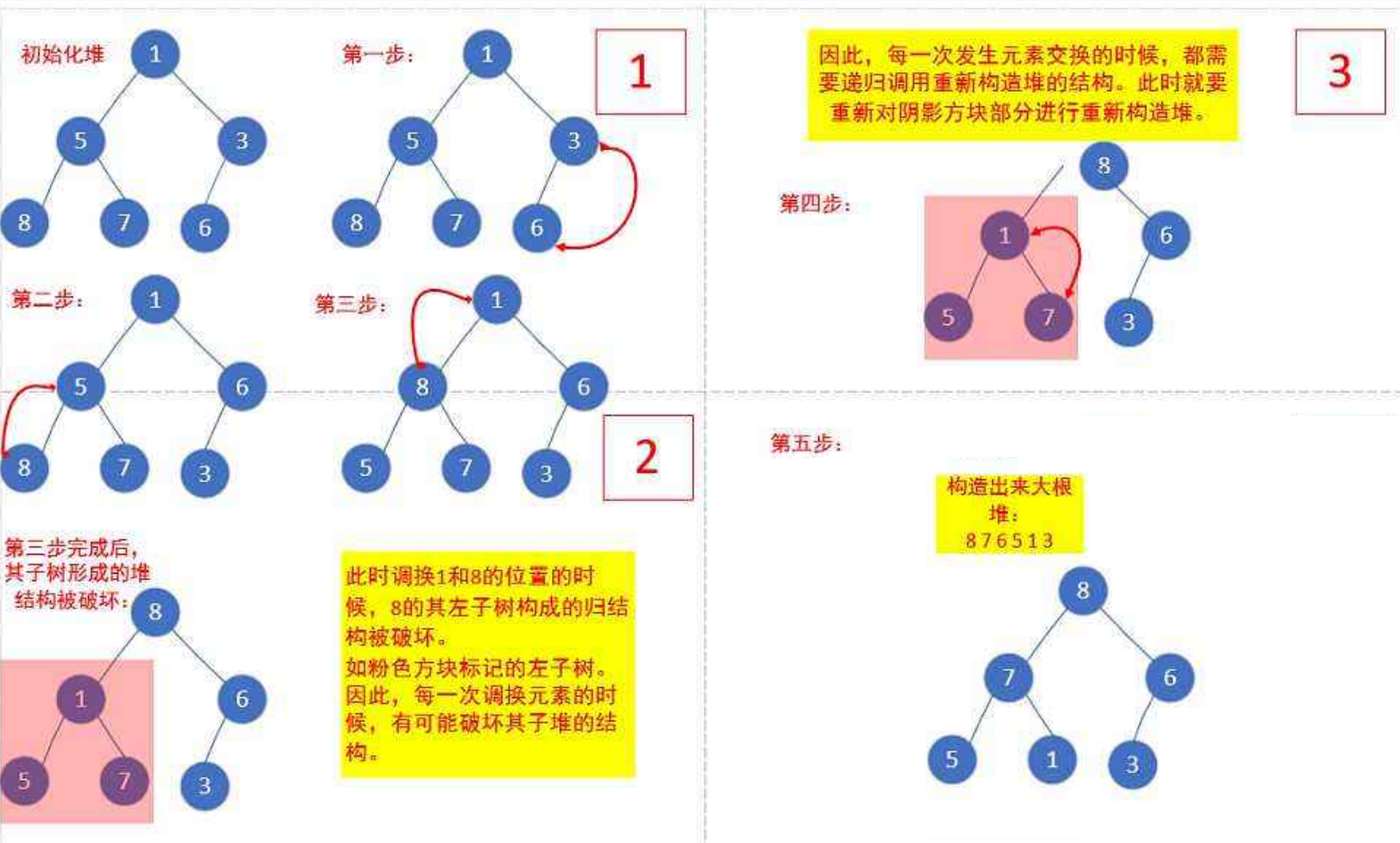
关键步骤(以数组 a[] = {1,5,3,8,7,6} 构建大堆为例 ):
- 定位倒数第一个非叶子节点:
数组长度n = 6,倒数第一个非叶子节点下标(n/2)-1 = 2(值3)。 - 从下往上调整子树:
- 调整下标 2(值
3)的子树:
左右子节点下标5(值6),因构建大堆需父 ≥ 子,3 < 6,交换 → 数组变为{1,5,6,8,7,3}。 - 调整下标 1(值
5)的子树:
左右子节点下标3(值8)、4(值7),选更大的8比较,5 < 8,交换 → 数组变为{1,8,6,5,7,3}。 - 调整下标 0(值
1)的子树:
左右子节点下标1(值8)、2(值6),选更大的8比较,1 < 8,交换 → 数组变为{8,1,6,5,7,3}。
交换后,下标1的1需继续调整其左右子树(下标3、4,值5、7):1 < 5,交换 → 数组变为{8,5,6,1,7,3}。- 下标
3的1继续调整,左右子节点无(或值更大 ),调整结束。
- 调整下标 2(值
代码实现(C 语言,大堆创建 ):
void CreateHeap(int* a, int n) {// 从倒数第一个非叶子节点开始调整for (int i = (n/2)-1; i >= 0; i--) {AdjustDown(a, n, i); // 复用向下调整函数(需适配大堆逻辑,修改比较符号)}
}
// 注意:AdjustDown 需修改为大堆逻辑(孩子比父大则交换)
示例验证:
调整后数组 {8,7,6,5,1,3}(最终大堆形态 ),满足大堆性质(父节点 ≥ 左右子节点 ),如根节点 8 ≥ 7 且 8 ≥ 6 ,下标 1 的 7 ≥ 5 且 7 ≥ 1 等。
3.2.3 建堆时间复杂度
因为堆是完全二叉树,而满二叉树也是完全二叉树,此处为了简化使用满二叉树来证明(时间复杂度本来看的就是近似值,多几个节点不影响最终结果):

因此:建堆的时间复杂度为O(N)。
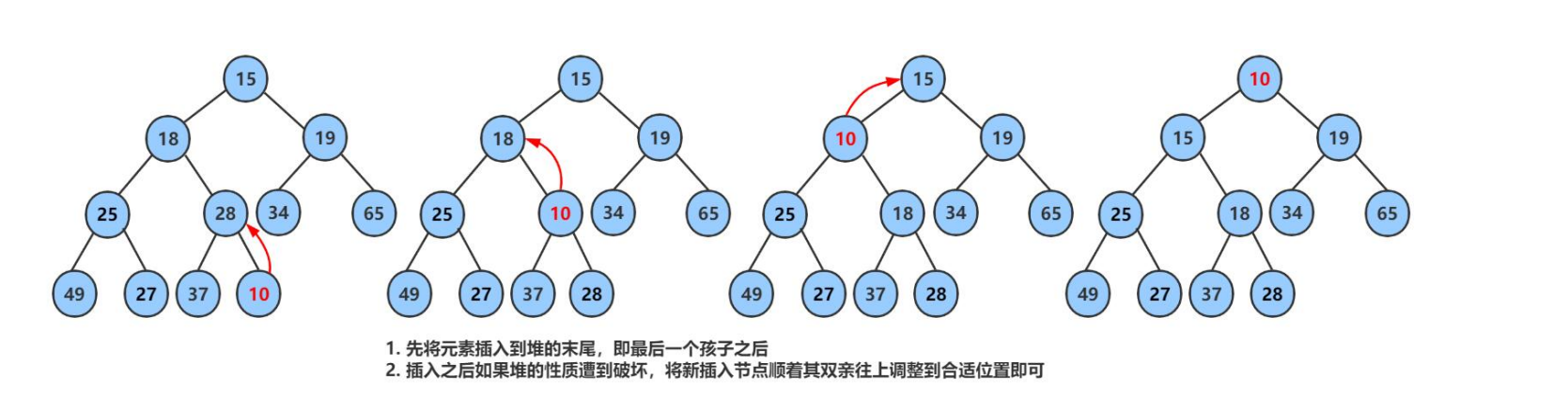
3.2.4 堆的插入
先插入一个10到数组的尾上,再进行向上调整算法,直到满足堆。
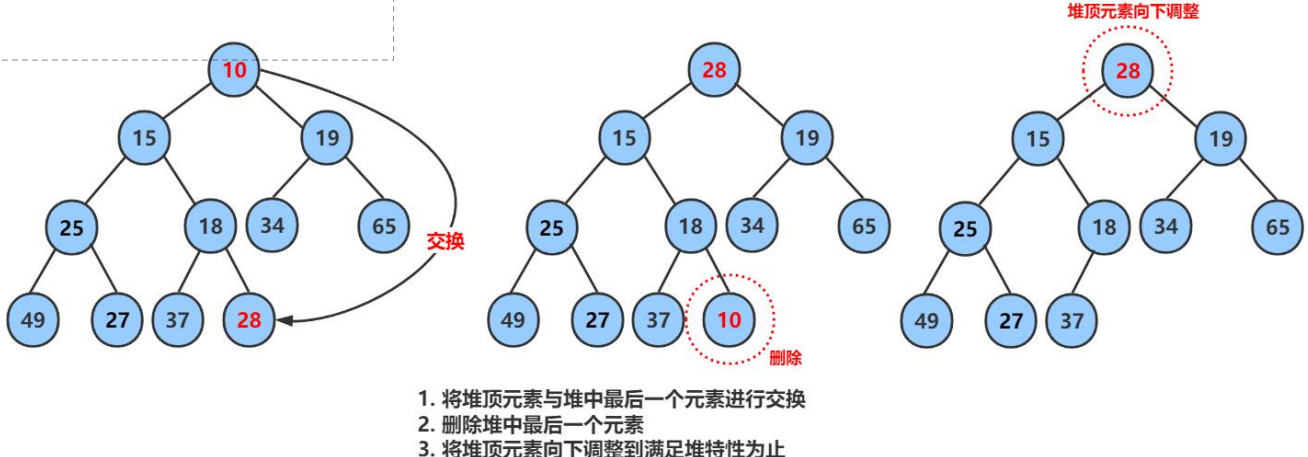
3.2.5 堆的删除
删除堆是删除堆顶的数据,将堆顶的数据根最后一个数据一换,然后删除数组最后一个数据,再进行向下调整算法。
3.2.6 堆的代码实现
一、代码功能模块梳理
模块划分:
代码实现了堆的基础操作,包含初始化、销毁、插入、删除、取堆顶、判空、size 获取,以及核心的 AdjustDown(向下调整 )和 AdjustUp(向上调整 )算法。
依赖关系:
AdjustDown/AdjustUp是堆结构维护的核心,用于保证堆的性质(小堆:父≤子 )。- 其他操作(
HeapPush/HeapPop)依赖这两个调整函数修复堆结构。
二、关键函数解析
1. 交换函数 Swap
作用:交换两个堆数据的值,为调整操作提供基础。
实现:
void Swap(HPDataType* p1, HPDataType* p2) {HPDataType tmp = *p1;*p1 = *p2;*p2 = tmp;
}
特点:直接操作指针,交换效率高,支持任意可赋值的 HPDataType(如 int、自定义结构体 )。
2. 向下调整 AdjustDown(小堆 )
作用:在“左右子树已是小堆”的前提下,从 root 开始向下调整,使当前子树满足小堆性质(父≤子 )。
实现逻辑:
- 定位左孩子
child = parent * 2 + 1。 - 选左右孩子中较小的(保证小堆 ):
if (child + 1 < n && a[child] > a[child + 1]) child++; - 若父节点 > 子节点,交换并递归调整子节点:
if (a[parent] > a[child]) {Swap(&a[parent], &a[child]);parent = child;child = parent * 2 + 1;
} else break;
示例验证:
数组{27,15,19,18,28,34,65,49,25,37},调整根节点(27 )后,逐步交换得到小堆。
3. 堆初始化 HeapInit
作用:从数组构建堆,需先拷贝数据,再通过 AdjustDown 从底层非叶子节点向上调整。
关键步骤:
- 动态分配内存并拷贝数据:
php->_a = (HPDataType*)malloc(sizeof(HPDataType)*n);memcpy(php->_a, a, sizeof(HPDataType)*n);
- 从倒数第一个非叶子节点开始调整(确保子树已为堆 ):
for (int i = (n - 1 - 1) / 2; i >= 0; i--) {AdjustDown((php->_a, n, i);
}
4. 堆销毁 HeapDestory
作用:释放堆的动态内存,重置成员变量。
实现:
void HeapDestory(Heap* php) {assert(php);free(php->_a);php->_a = NULL;php->_size = 0; php->_capacity = 0;
}
5. 向上调整 AdjustUp(小堆 )
作用:插入新节点后,从最后一个节点向上调整,修复堆性质(保证父≤子 )。
实现逻辑:
- 定位父节点
parent = (child - 1) / 2。 - 若子节点 < 父节点,交换并递归调整父节点:
if (a[child] < a[parent]) {Swap(&a[child], &a[parent]);child = parent;parent = (child - 1) / 2;} else break;
应用场景:
HeapPush 中插入新节点到数组末尾后,调用此函数调整堆。
6. 堆插入 HeapPush
作用:向堆中添加元素,自动扩容并修复堆性质。
步骤:
- 检查容量,满则扩容(
realloc):if (php->_capacity == php->_size) {php->_capacity *= 2;HPDataType* tmp = realloc(php->_a, sizeof(HPDataType)*php->_capacity);php->_a = tmp; }
- 插入元素到末尾,调用 AdjustUp 调整:
php->_a[php->_size] = x;
php->_size++;
AdjustUp(php->_a, php->_size, php->_size - 1);
注意:
扩容后需更新 _capacity,realloc 可能失败,需判断(代码中未处理,生产环境需完善 )。
7. 堆删除 HeapPop(删除堆顶 )
作用:删除堆顶元素(小堆的最小值 ),通过交换堆顶与最后一个元素、缩小规模、向下调整修复堆。
步骤:
- 交换堆顶与最后一个元素:
Swap(&php->_a[0], &php->_a[php->_size - 1]); php->_size--; - 从堆顶开始向下调整:
AdjustDown(php->_a, php->_size, 0);
8. 堆顶获取 HeapTop
作用:返回堆顶元素(小堆的最小值 )。
实现:
HPDataType HeapTop(Heap* php) {assert(php);return php->_a[0];
}
9. 判空与 size 获取
HeapEmpty:
bool HeapEmpty(Heap* php) {assert(php);return php->_size == 0; // 原代码 php->size 错误,成员是 _size
}
HeapSize:
int HeapSize(Heap* php) {assert(php);return php->_size;
}
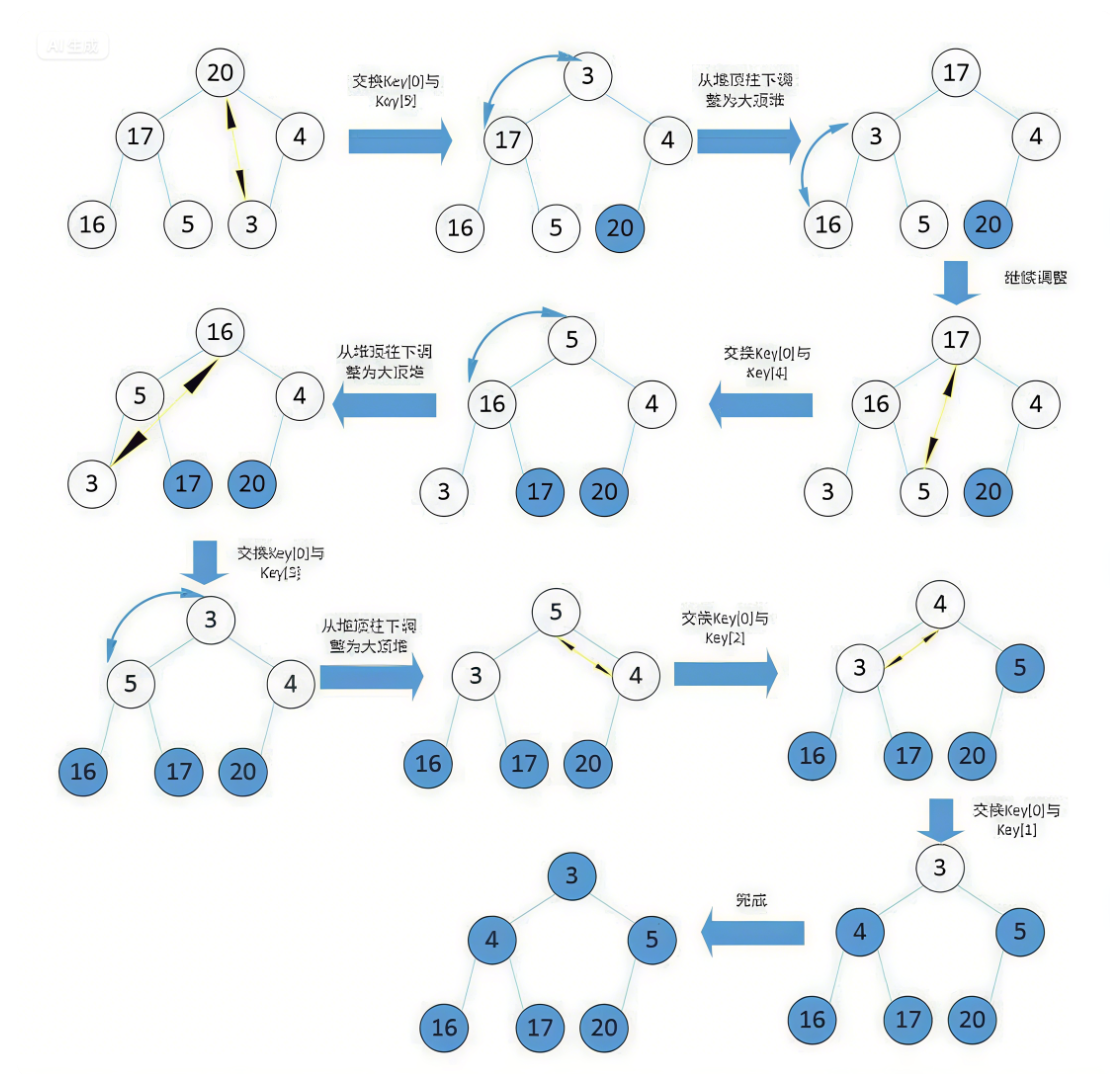
4. 堆的实际运用 - 堆排序
4.1 堆排序核心原理
核心逻辑:
堆排序借助堆的“选择极值高效性”,通过建堆 + 交换删除两个阶段,将无序数组转化为有序序列。利用大堆(升序)或小堆(降序)的特性,每次将当前极值(大堆的堆顶最大值)交换到数组末尾,逐步完成排序。
本质:
把堆结构的“极值提取”能力,转化为排序的“有序放置”过程,核心依赖 向下调整 算法维持堆性质。
4.2 升序排序 - 建大堆的必要性
若直接用小堆实现升序,逻辑上需每次提取最小元素(堆顶),然后对剩余元素重建堆。但存在关键缺陷:
-
小堆升序的时间复杂度问题:
- 建小堆:
O(n)(或O(n log n),取决于建堆方式 )。 - 每次提取最小元素后,重建堆需
O(log n),共n次 → 总复杂度O(n log n)。 - 但实际重建堆时,需频繁移动数据(如数组拷贝剩余元素 ),实际运行效率极低(甚至劣于冒泡排序 )。
- 建小堆:
-
大堆升序的优化逻辑:
- 建大堆:
O(n)(从底层非叶节点向上调整 )。 - 利用“堆删除思想”:交换堆顶(最大值)与数组末尾元素 → 最大值“归位”到正确位置;然后对剩余元素(前
n-1个 )向下调整重建大堆 → 时间复杂度O(log n)。 - 循环
n-1次后,数组完成升序排列。
- 建大堆:
对比示例(数组 [4,6,2,8,1] 升序排序 ):
- 小堆方案:
建小堆后堆顶是1,交换到末尾 → 剩余数组[4,6,2,8]需重建小堆(O(log 4));重复5次 → 低效。 - 大堆方案:
建大堆后堆顶是8(最大值 ),交换到末尾 → 剩余数组[4,6,2,1]向下调整重建大堆(O(log 4));重复4次 → 高效。
结论:
升序排序选大堆,可复用“交换堆顶 + 局部向下调整”逻辑,避免频繁全数组重建堆,时间复杂度稳定为 O(n log n) 。
4.3 堆排序完整流程(升序 - 大堆实现 )
步骤 1:建大堆
对无序数组,从倒数第一个非叶节点开始,依次 向下调整 ,构建大堆。
示例:
数组 [4,6,2,8,1] → 建大堆后: 对应数组:[8,6,2,4,1]
步骤 2:交换堆顶与末尾,缩小堆规模
- 交换堆顶(最大值
8)与数组末尾(1)→ 数组变为[1,6,2,4,8]。 - 堆规模减
1(仅需处理前4个元素 )。
步骤 3:向下调整重建大堆
对前 4 个元素([1,6,2,4] )从堆顶 向下调整 ,重建大堆: 对应数组:[6,4,2,1,8]
步骤 4:循环执行“交换 + 调整”
重复步骤 2-3,直到堆规模为 1:
- 第二次循环:交换
6与1→[1,4,2,6,8]→ 调整前3个元素 → 大堆[4,1,2]→ 数组[4,1,2,6,8]。 - 第三次循环:交换
4与2→[2,1,4,6,8]→ 调整前2个元素 → 大堆[2,1]→ 数组[2,1,4,6,8]。 - 第四次循环:交换
2与1→[1,2,4,6,8]→ 调整前1个元素(无需调整 )。
最终结果:
数组升序排列为 [1,2,4,6,8] 。
代码实现(C 语言 ):
// 向下调整(大堆)
void AdjustDown(int* a, int n, int root) {int parent = root;int child = parent * 2 + 1;while (child < n) {// 选左右孩子中较大的(大堆)if (child + 1 < n && a[child] < a[child + 1]) {child++;}if (a[parent] < a[child]) {Swap(&a[parent], &a[child]);parent = child;child = parent * 2 + 1;} else {break;}}
}// 堆排序(升序)
void HeapSort(int* a, int n) {// 步骤 1:建大堆for (int i = (n - 1 - 1) / 2; i >= 0; i--) {AdjustDown(a, n, i);}// 步骤 2-4:交换 + 调整int end = n - 1;while (end > 0) {Swap(&a[0], &a[end]); // 交换堆顶与末尾AdjustDown(a, end, 0); // 调整前 end 个元素end--;}
}
4.4 堆排序的时间与空间复杂度
时间复杂度:
- 建堆:
O(n)(从底层向上调整,实际操作次数少于n)。 - 排序阶段:
n-1次向下调整,每次O(log n)→ 总复杂度O(n log n)。 - 最终:堆排序整体时间复杂度为
O(n log n),优于冒泡、选择排序(O(n²))。
空间复杂度:
仅使用常数级额外空间(Swap 临时变量 ),空间复杂度为 O(1) ,属于原地排序。
稳定性:
因排序过程中存在“远距离交换”(如大堆顶与末尾元素交换 ),相同值可能改变相对位置 → 堆排序是不稳定排序。
示例:
数组 [5,5,3] 建大堆后交换堆顶(5 )与末尾(3 )→ [3,5,5] → 调整后大堆 [5,3] → 交换后 [3,5,5] → 最终有序数组 [3,5,5] 。若原数组是 [5a,5b,3] ,排序后可能变为 [3,5b,5a] → 破坏稳定性。
4.5 TOP-K 问题
4.5.1 问题定义与核心痛点
TOP-K问题:
从海量数据(数据量 N 极大,可能无法全部加载到内存)中,筛选出前 K 个最大元素(或最小元素)。
示例:从10亿条订单数据中找消费最高的前100名用户;从百万首歌曲中找播放量前50的歌曲。
核心痛点:
- 直接排序不可行:对
N个数据排序的时间复杂度为O(N log N),且N极大时内存无法容纳全部数据。 - 需高效、低空间消耗的方案:利用堆的“局部极值管理”特性,仅维护
K个元素的堆,实现流式处理。
4.5.2 堆解法核心思路
核心逻辑:
通过维护一个大小为 K 的堆,用剩余数据与堆顶元素比较,动态替换非目标元素,最终堆中保留的就是前 K 个目标元素。
具体策略:
-
求前
K个最大元素:- 用前
K个元素建小堆(堆顶是当前K个中最小的)。 - 剩余
N-K个元素依次与堆顶比较:若元素 > 堆顶,说明该元素比当前K个中最小的还大,应加入堆 → 替换堆顶,再向下调整维持小堆性质。 - 最终堆中
K个元素即为前K个最大元素(堆顶是这K个中最小的,其余均比它大)。
- 用前
-
求前
K个最小元素:- 用前
K个元素建大堆(堆顶是当前K个中最大的)。 - 剩余
N-K个元素依次与堆顶比较:若元素 < 堆顶,说明该元素比当前K个中最大的还小,应加入堆 → 替换堆顶,再向下调整维持大堆性质。 - 最终堆中
K个元素即为前K个最小元素(堆顶是这K个中最大的,其余均比它小)。
- 用前
为什么前K大建小堆?:
小堆的堆顶是当前 K 个元素的“门槛”,只有比门槛大的元素才配进入堆,保证堆中始终是候选的最大元素;若建大堆,堆顶是当前最大,无法有效筛选更大的元素(新元素比堆顶小仍可能是前K大,但无法判断)。
4.5.3 示例:求前 3 个最大元素
数据场景:
数组 a[] = {12, 3, 5, 7, 1, 9, 15, 8, 6},N=9,K=3(找前3个最大元素)。
步骤拆解:
-
取前K个元素建小堆:
前3个元素[12, 3, 5]→ 建小堆(堆顶为3):
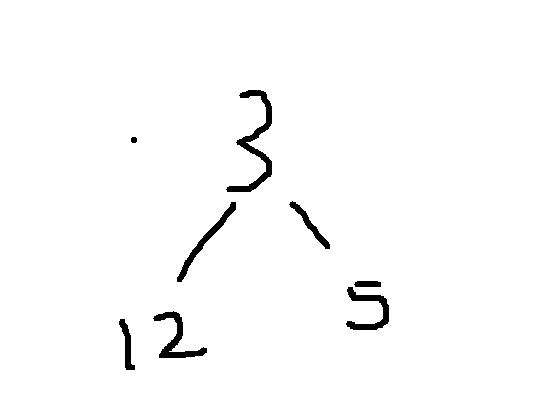
-
剩余元素依次比较替换:
- 元素7:7 > 堆顶3 → 替换堆顶 →
[7, 12, 5]→ 向下调整维持小堆: 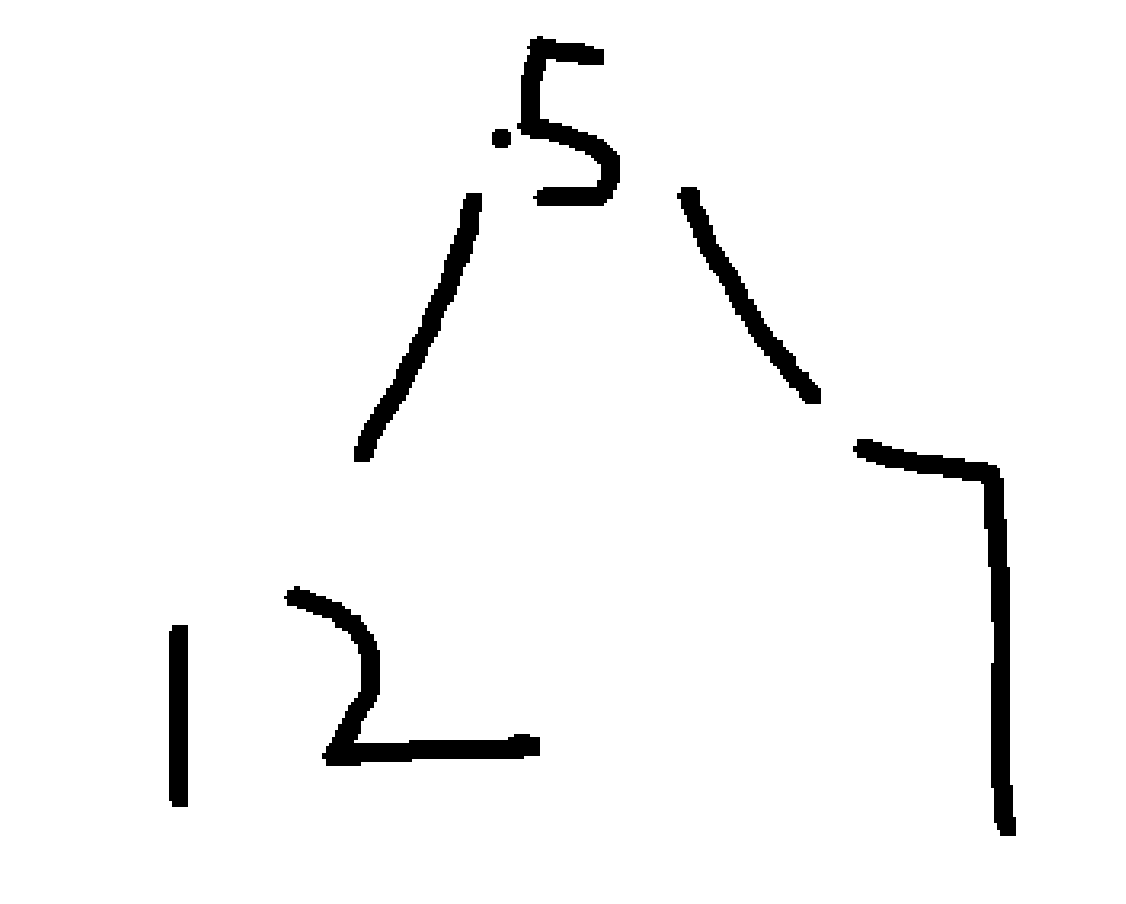
- 元素1:1 < 堆顶5 → 不替换。
- 元素9:9 > 堆顶5 → 替换堆顶 →
[9, 12, 7]→ 向下调整维持小堆: 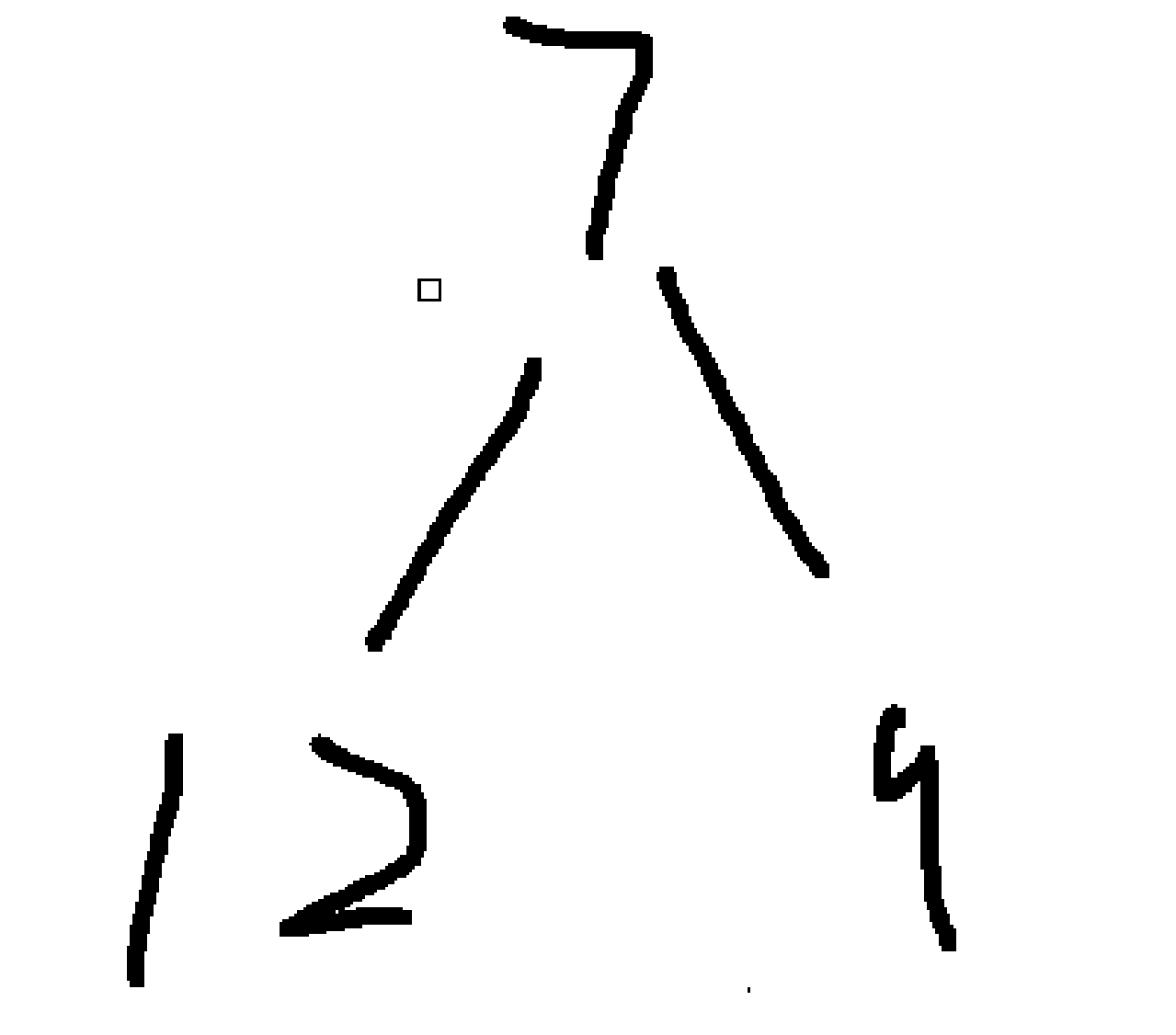
- 元素15:15 > 堆顶7 → 替换堆顶 →
[15, 12, 9]→ 向下调整维持小堆: 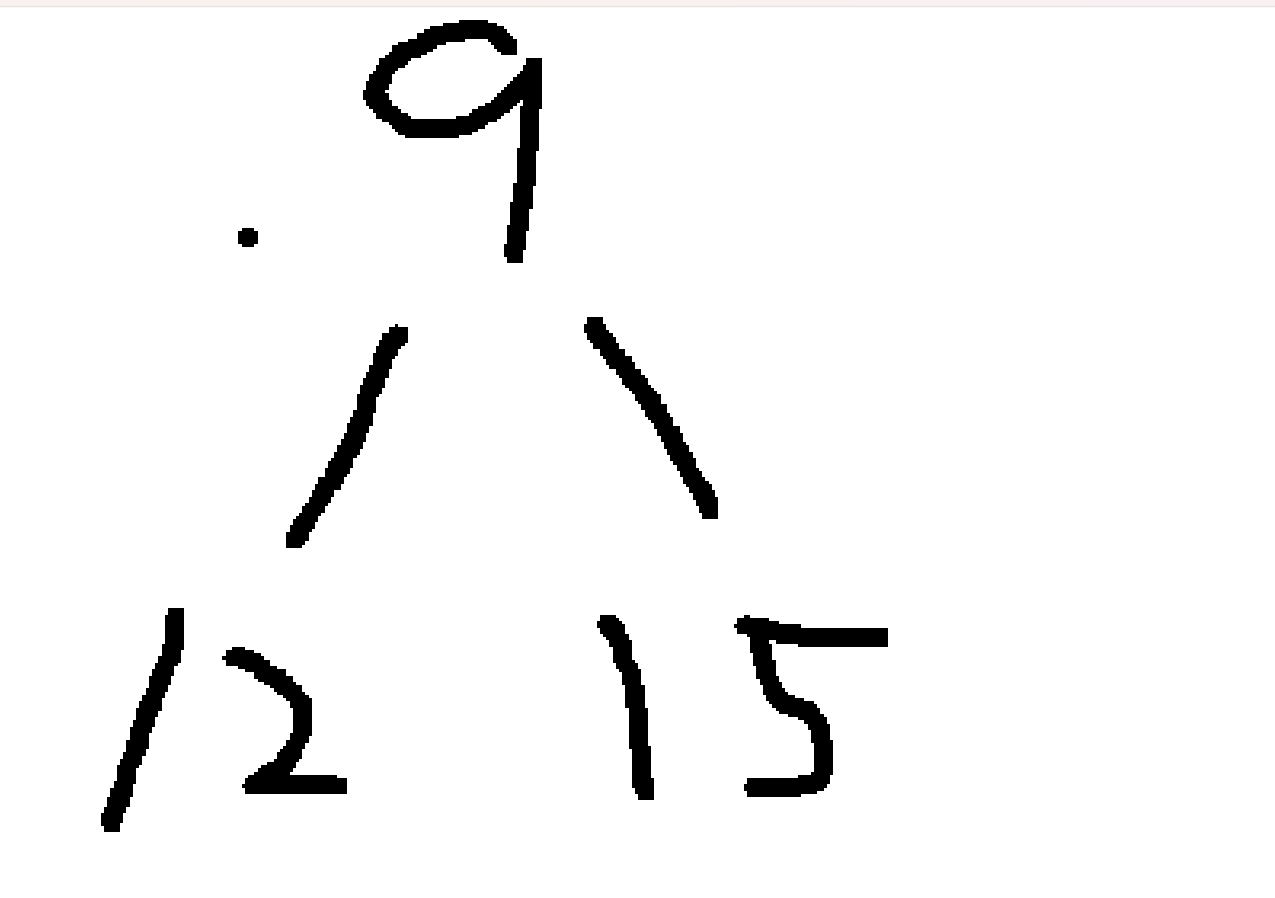
- 元素8:8 < 堆顶9 → 不替换。
- 元素6:6 < 堆顶9 → 不替换。
- 最终结果:
堆中元素[9, 12, 15]→ 前3个最大元素为9, 12, 15(实际排序后前3大为15,12,9,结果一致)。
4.5.4 代码实现:PrintTopK 函数
函数功能:
从数组 a(大小 n)中打印前 k 个最大元素(基于小堆实现)。
完整代码:
// 向下调整(小堆,用于维护前K大元素的堆)
void AdjustDown(int* a, int n, int root) {int parent = root;int child = parent * 2 + 1;while (child < n) {// 选左右孩子中较小的if (child + 1 < n && a[child] > a[child + 1]) {child++;}// 父 > 子,交换并继续调整if (a[parent] > a[child]) {Swap(&a[parent], &a[child]);parent = child;child = parent * 2 + 1;} else {break;}}
}// 打印前K个最大元素
void PrintTopK(int* a, int n, int k) {assert(a && n > 0 && k > 0 && k <= n);// 步骤1:用前k个元素建小堆(堆顶是当前k个中最小的)for (int i = (k - 1 - 1) / 2; i >= 0; i--) {AdjustDown(a, k, i);}// 步骤2:剩余n-k个元素依次与堆顶比较,满足条件则替换并调整for (int i = k; i < n; i++) {if (a[i] > a[0]) { // 当前元素比堆顶大,应加入候选集a[0] = a[i]; // 替换堆顶AdjustDown(a, k, 0); // 调整维持小堆}}// 打印堆中k个元素(前k个最大元素)for (int i = 0; i < k; i++) {printf("%d ", a[i]);}printf("\n");
}
代码解析:
- 建堆阶段:对前 k 个元素从底层非叶节点向上调整,构建小堆(O(k) 时间)。
- 筛选阶段:遍历剩余 n-k 个元素,每次比较替换后调整堆(O((n-k) log k) 时间)。
- 总时间复杂度:O(n log k),远优于排序的 O(n log n)(尤其 n 极大时)。
- 空间复杂度:O(1)(原地操作),适合大数据场景(无需加载全部数据到内存,可流式读取)。
4.5.5 堆解法的优势与适用场景
优势:
- 时间效率高:总时间复杂度
O(n log k),k远小于n时(如k=100,n=1e9),效率远高于排序。 - 空间消耗低:仅需维护
k个元素的堆,空间复杂度O(k),适合内存有限的场景。 - 支持流式处理:无需一次性加载全部数据,可从文件/网络流中逐批读取数据,边读边处理。
适用场景:
- 海量数据(
n极大,无法全量加载)。 - 只需前
k个极值,无需整体排序。 - 内存资源有限的嵌入式设备、服务器端数据处理等。
对比排序法:
| 方案 | 时间复杂度 | 空间复杂度 | 适合场景 |
|---|---|---|---|
| 直接排序 | O(n log n) | O(1) | 数据量小(n 较小) |
| 堆解法 | O(n log k) | O(k) | 数据量大(n 极大) |
