堆(Java实现)
一:堆(PriorityQueue)
1:堆的概念:
如果有一个关键码的集合K = {k0,k1, k2,…,kn-1},把它的所有元素按完全二叉树的顺序存储方式存储 在一个一维数组中,并满足:Ki <= K2i+1 且 Ki<= K2i+2 (Ki >= K2i+1 且 Ki >= K2i+2) i = 0,1,2…,则称为 小堆(或大堆)。将根节点最大的堆叫做最大堆或大根堆,根节点最小的堆叫做最小堆或小根堆。
2:堆的性质
1:堆中某个节点的值总是不大于或不小于其父节点的值;2:堆总是一棵完全二叉树
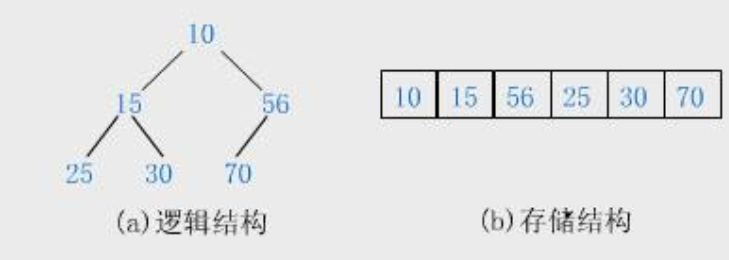
1:小根堆:
根的值总是小于左子树和右子树,存储结果是采用层序遍历的结果。
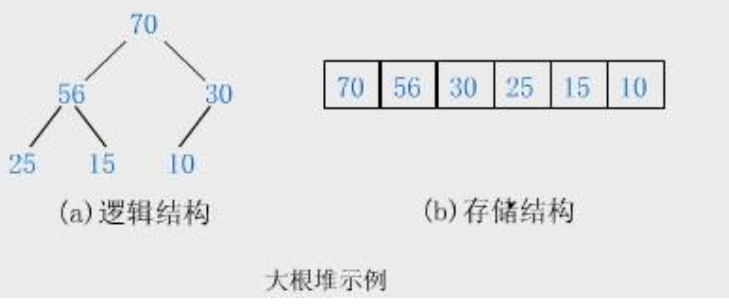
2:大根堆
根的值总是大于左子树和右子树,存储结构是采用层序遍历的结果。
3:堆的存储方式
从堆的概念可知,堆是一棵完全二叉树,因此可以层序的规则采用顺序的方式来高效存储,
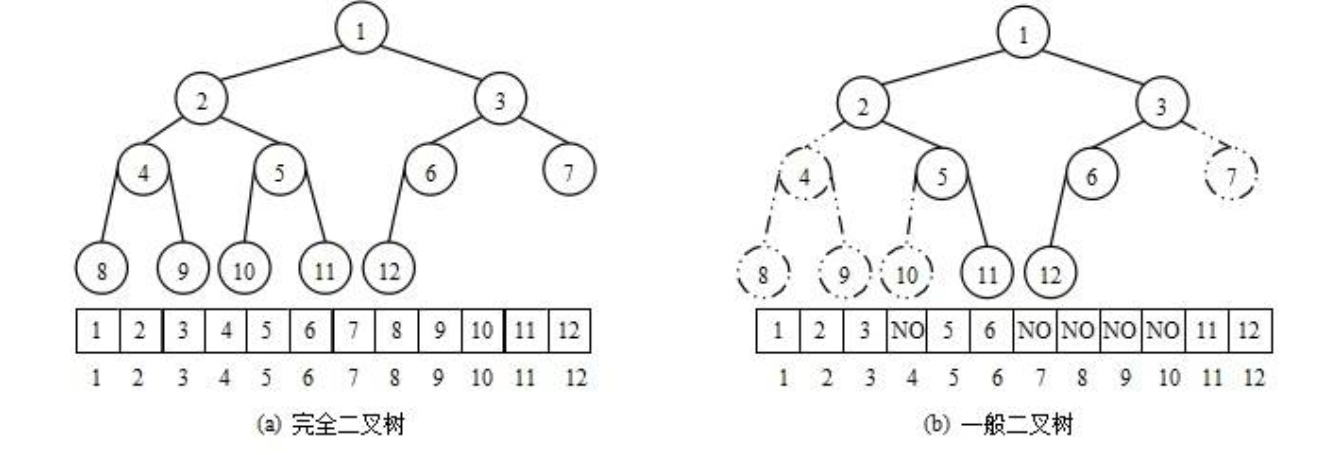
注意:对于非完全二叉树,则不适合使用顺序方式进行存储,因为为了能够还原二叉树,空间中必须要存储空节点,就会导致空间利用率比较低。
将元素存储到数组中后,可以根据二叉树章节的性质对树进行还原。假设i为节点在数组中的下标,则有:
1:如果i为0,则i表示的节点为根节点,否则i节点的双亲节点为 (i - 1)/2
2:如果2 * i + 1 小于节点个数,则节点i的左孩子下标为2 * i + 1,否则没有左孩子(左孩子表示方式是:2 * i + 1)
3:如果2 * i + 2 小于节点个数,则节点i的右孩子下标为2 * i + 2,否则没有右孩子(右孩子表示方式是:2 * i + 2)
4:堆的创建
4.1:采用向下调整的方式创建堆
4.1.1:大根堆(小根堆只需要将下述的if语句代码改为<即可):
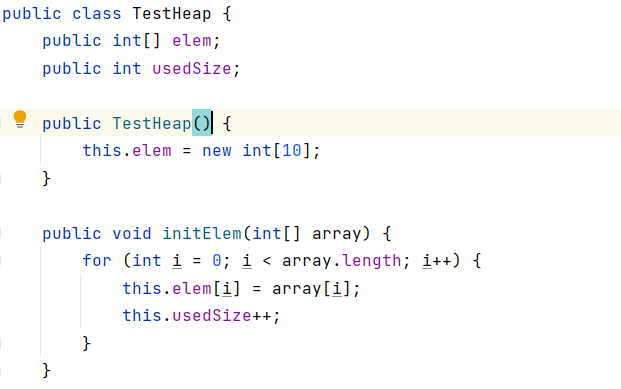
初始化数组:
对要排序的数组进行初始化,用userSize代表数组元素的个数,elem数组存储传入的数组元素。
4.1.2:向下调整(shifDown):
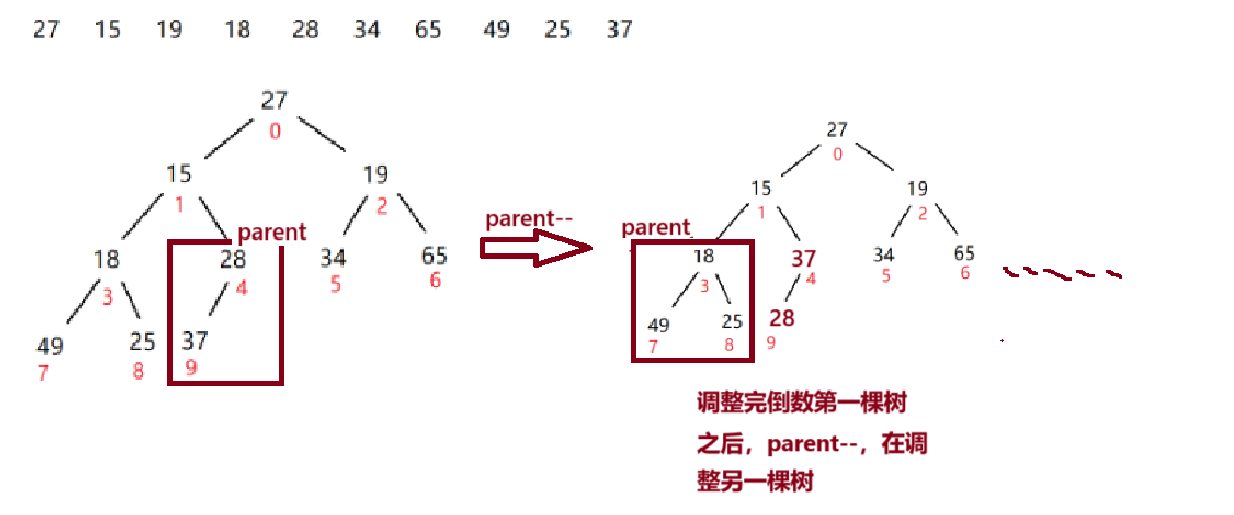
从最后一颗子树开始调整为大根堆,假设最后一棵树的根节点为parent,然后从parent所在的子树开始逐一调整,没调整一颗树parent就parent--,parent然后跳转到倒数第二课树,然后再将此树调整为大根堆。parent=(userSize-1-1)/2
注意:已知孩子节点下标为i 则双亲节点的值是多少?(i-1)/2
已知父亲节点下标为i
左孩子:2*i+1;右孩子:2*i+2

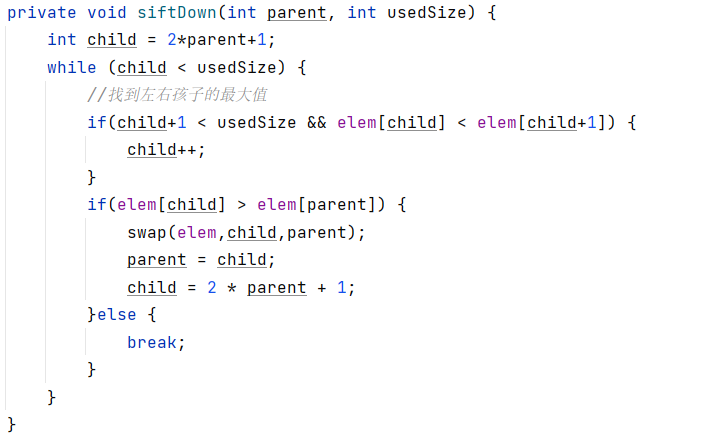
那么,siftDown方法如何编写呢,siftDown方法实现的是根节点与子节点的最大时比较,然后parent与子节点中的最大值交换位置,这样就实现了子树的大根堆。


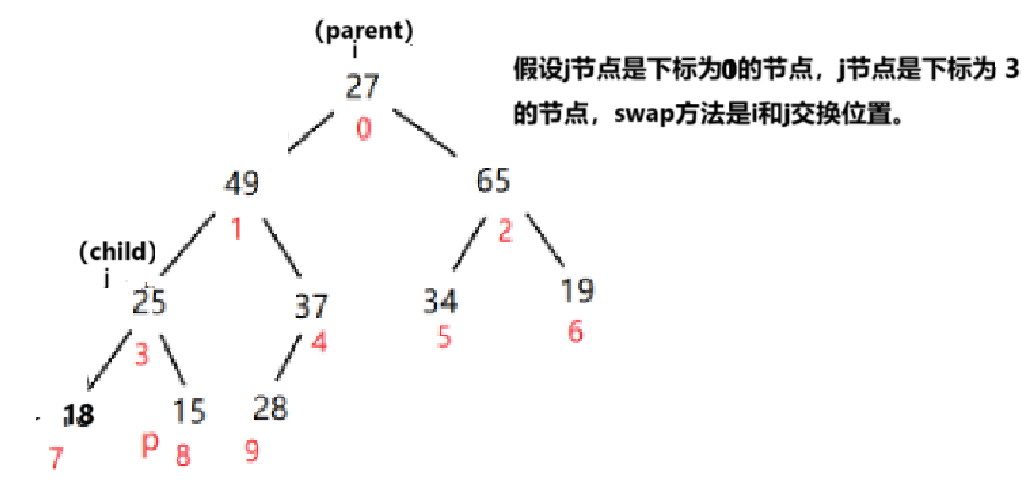
swap方法是任意两个传过来的节点都可以交换位置,不只parent节点和child节点:
整个过程: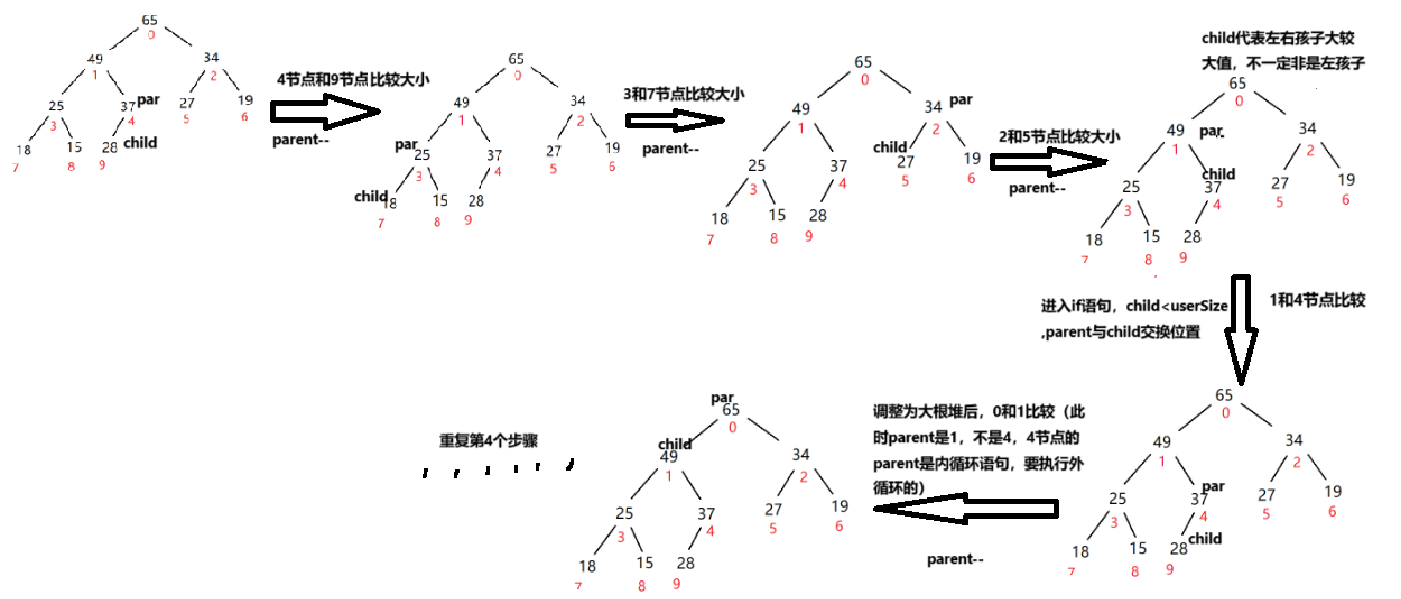
shifDown时间复杂度分析:
从根一路比较到叶子,比较的次数为完全二叉树的高度,即时间复杂度为logN
4.1.3:建根的时间复杂度:
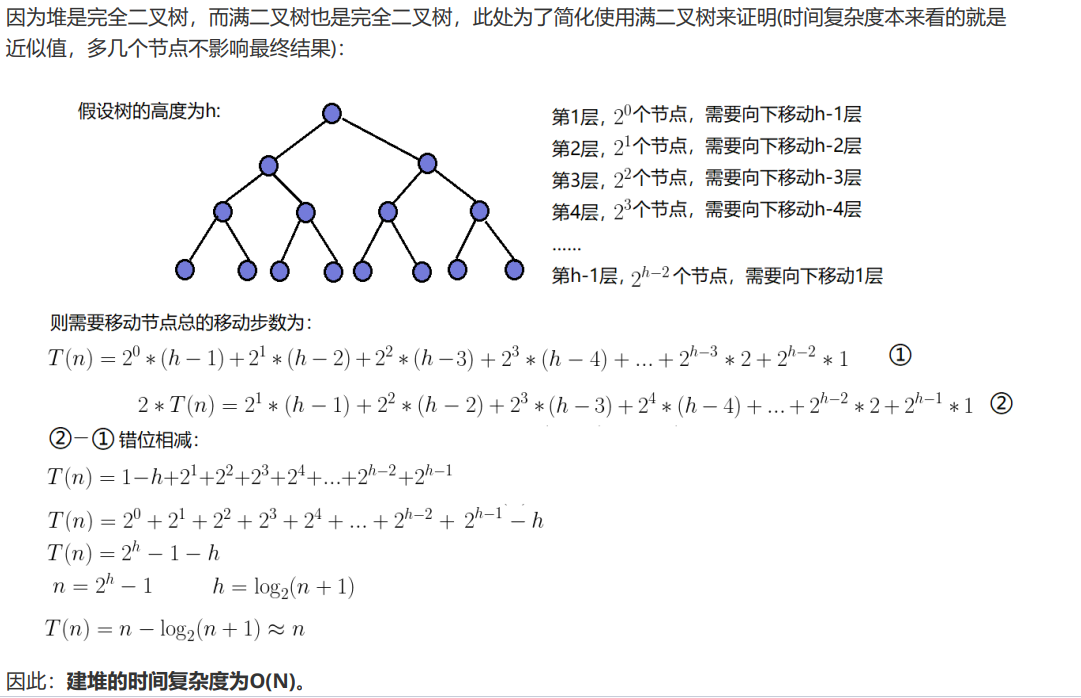
向上调整(shifUp):
向上调整是接收一个孩子节点的参数的位置,然后确定这个孩子节点的根节点parent,然后逐一遍历调整。
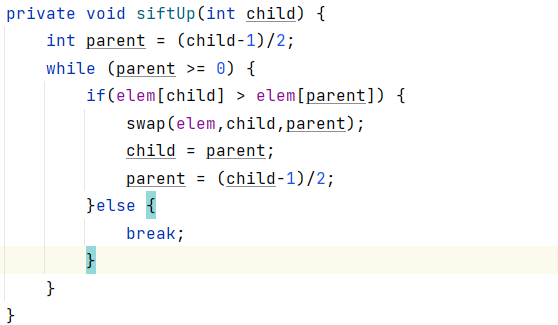
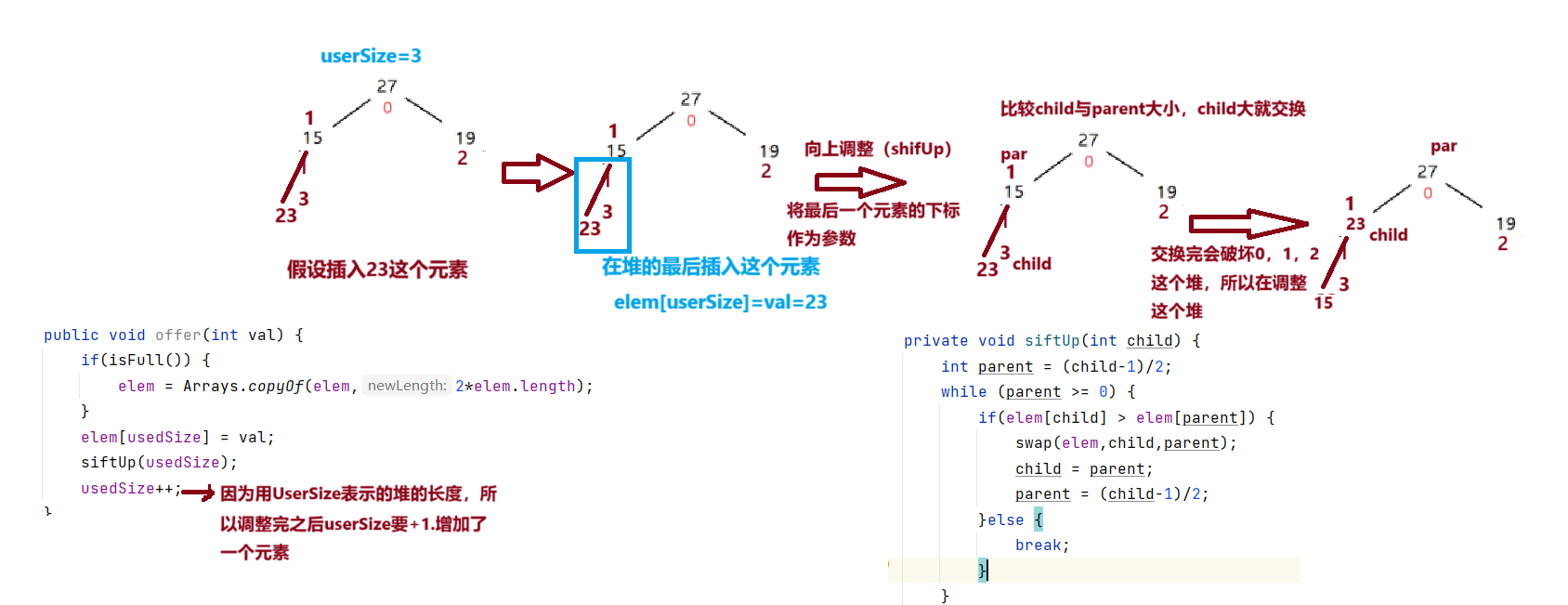
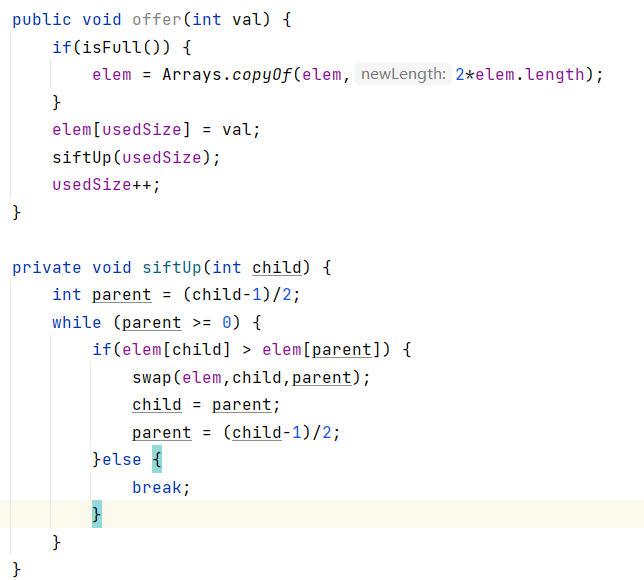
5:堆的插入(offer):
首先判断是否数组已满,已满扩容,然后在堆的末尾节点添加要插入val值,采用shifUp的形式对堆进行排序。
也可以直接用offer插入方法直接建大根堆,数组一开始为空,一个一个插入,然后一个一个调整。
![]()
6.堆的删除(delete)
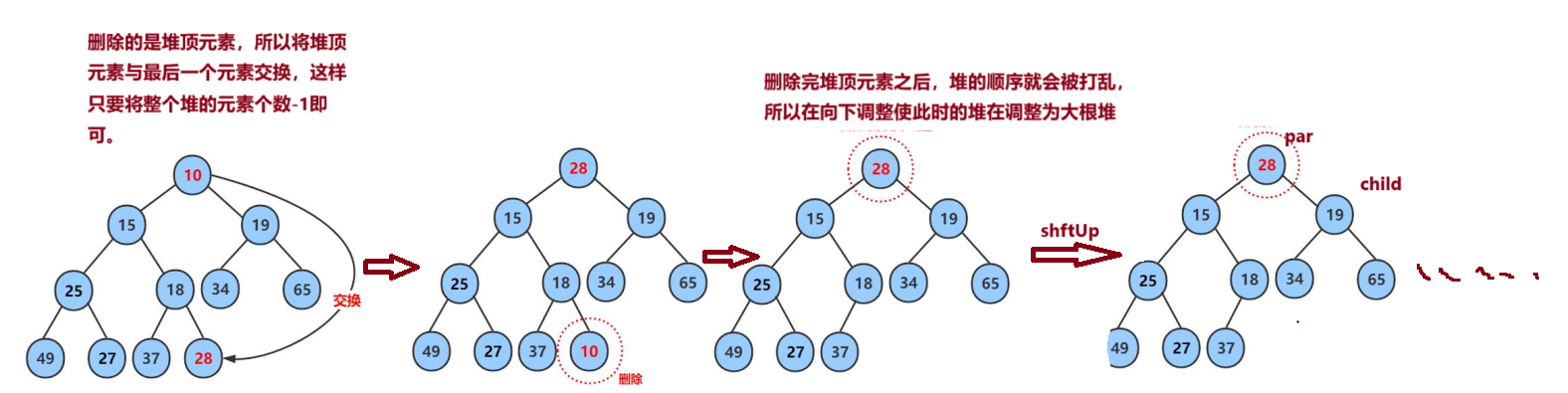
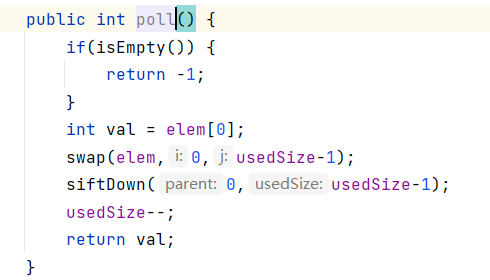
注意:堆的删除一定删除的是堆顶元素。具体如下:
1:将堆顶元素对堆中最后一个元素交换
2:将堆中有效数据个数减少一个
3:对堆顶元素进行向下调整
二 : 用接口介绍:
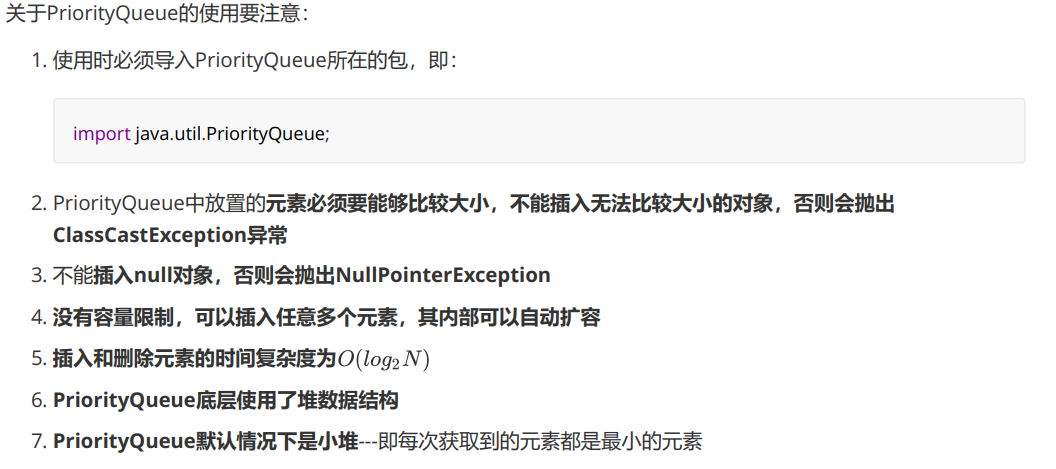
PriorityQueue的特性:
Java集合框架中提供了PriorityQueue和PriorityBlockingQueue两种类型的优先级队列,PriorityQueue是线程不安全的,PriorityBlockingQueue是线程安全的,主要介PriorityQueue。


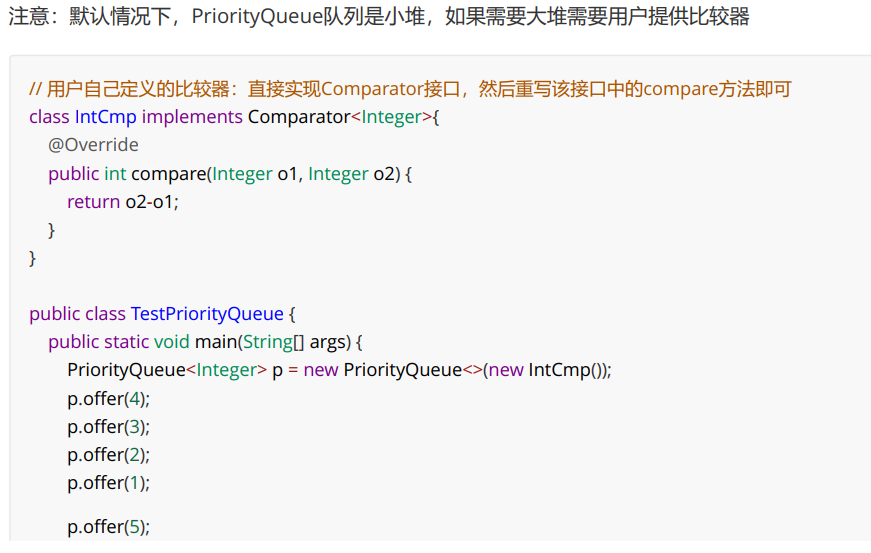
三:top-k问题:最大或者最小的前k个数据。
设计一个算法,找出数组中最小的k个数。以任意顺序返回这k个数均可。

求前k个最小的
1:整体排序
2:建立大小为k的小根堆
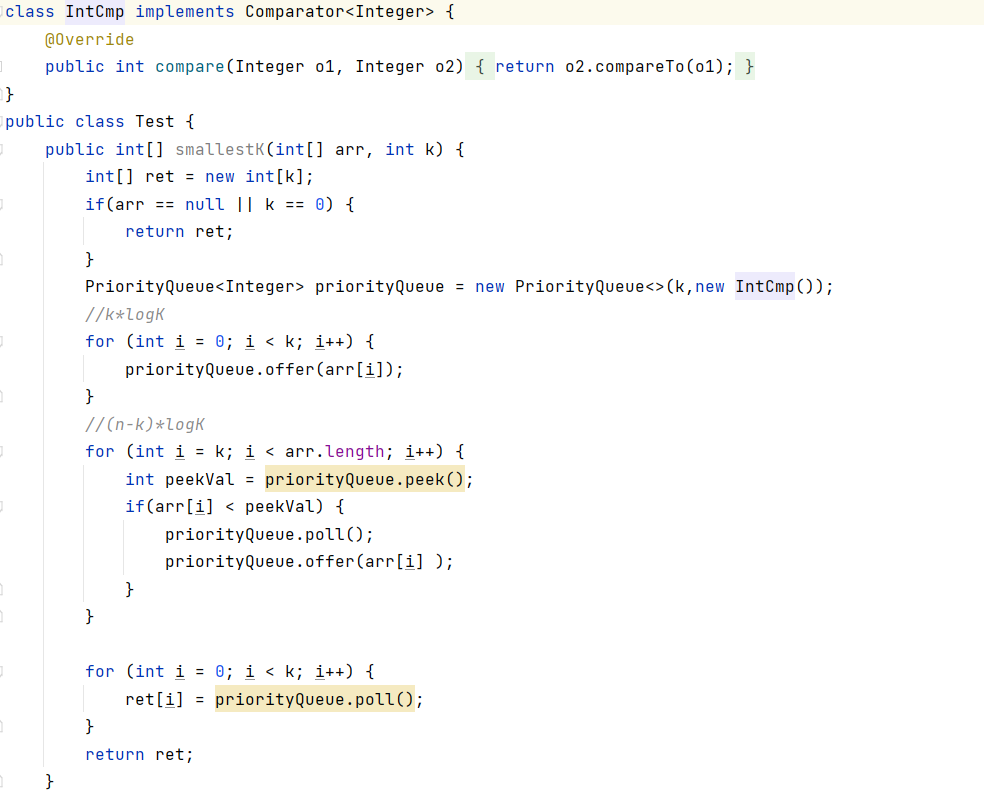
3:把前k个元素创建为大根堆,遍历剩下的N-k个元素,和堆顶比较,如果比堆顶小,则把堆顶删除,当前元素插入
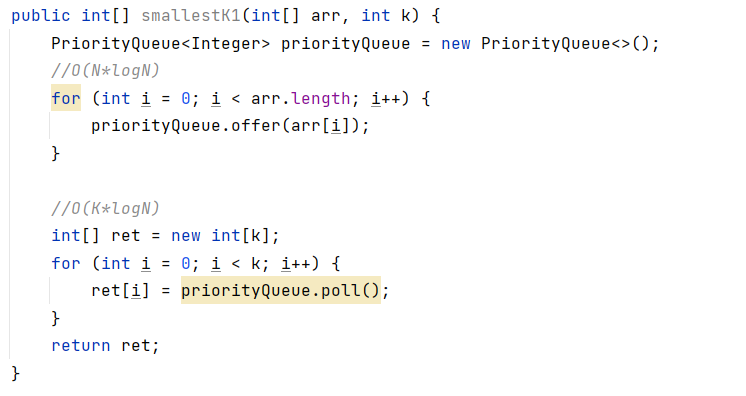
第二种方法实现:
直接建立小根堆,然后poll出前k个即可。
第三种方法的实现:

四:堆的应用
4.1 PriorityQueue的实现
用堆作为底层结构封装优先级队列
4.2 堆排序
堆排序即利用堆的思想来进行排序,总共分为两个步骤
1:建堆
升序: 建大堆
降序: 建小堆
2:利用堆删除思想来进行排序
建堆和堆删除中都用到了向下调整,因此掌握了向下调整,就可以完成堆排序
