diffusion原理和代码延伸笔记1——扩散桥，GOUB，UniDB

引言

扩散模型包含前向过程和反向过程，前向过程把数据分布映射成高斯分布，反向过程想复原之，不过这种映射是一整个分布和一整个分布之间的，学习的是如何从噪声中创造出新的数据。要是图像修复，去雨，超分，分子设计等需要点对点的任务，不怎么需要“创造”能力的任务，比如在药物设计中，我们可能需要生成一个起始构象和目标构象是固定的分子，在图像修复，去雨等问题上，可以理解为一对一的点任务。这一篇笔记介绍GOUB和更为广泛且纳入GOUB，VE，VP等为特殊情况的UniDB。

扩散桥

扩散桥，Diffusion Bridge，基于SDE，它要连接两个已知的端点，作为一个约束的限制。

与DDPM等基于马尔科夫链（离散化SDE）不同，扩散桥不再是关心$p({\mathbf{x}}_0)$，而是关心在已知 ${\mathbf{X}}_s={\mathbf{x}}_s$ 和 ${\mathbf{X}}_T={\mathbf{x}}_T$ 的情况下，中间状态 ${\mathbf{X}}_t,s<t<T$ 的条件概率分布$p({\mathbf{x}}_t|{\mathbf{x}}_s,{\mathbf{x}}_T)$。

从动态视角看，$p({\mathbf{x}}_t|{\mathbf{x}}_0,{\mathbf{x}}_T)$其实是一个随机过程，形象点说，描述了一个粒子从$t=0$的状态开始随机游走，最终被拉到${\mathbf{x}}_{\mathbf{T}}$这个终点。每一次实验下，路径都是随机的，这个粒子的位置也是不确定的。如果剖析一个时间点的话，就可以发现对于一个固定的${\mathbf{x}}_{\mathbf{t}}$，其概率分布是完全确定的，后文可以发现确定的是$p({\mathbf{x}}_t|{\mathbf{x}}_0,{\mathbf{x}}_T)\sim \mathcal{N}(mean,variance)$，这里先不给出平均值和方差的具体形式。

好，为了满足这个双端点约束，SDE方程需要做一些修改。
一个标准的SDE如下：
$$d{\mathbf{X}}_t=\mathbf{f}({\mathbf{X}}_t,t)dt+g_{t}d{\mathbf{W}}_t,{\mathbf{x}}_0\sim p({\mathbf{x}}_0)$$
其中 $\mathbf{f}({\mathbf{X}}_t,t)$ 是漂移项， $g(t)d{\mathbf{W}}_t$ 是扩散项。

接下来记录一种扩散桥的实现方式。

Doob’s h-transform

接下来是Generalized Ornstein-Uhlenbeck，一个基于OU方程扩展的sde，这是一个$t$趋于无穷会保持结果平稳的高斯-马尔可夫过程（线性上有wiener过程，线性组合是高斯分布，马尔可夫性质），任意时刻$t$的边际概率分布随时间$t$的增加会逐渐趋近于一个稳定的均值和方差：
$$\begin{array}{c}d{\mathbf{X}}_t={\theta }_t(\mathbf{\mu }-{\mathbf{X}}_t)dt+g_{t}d{\mathbf{W}}_t\end{array}$$

其中$\mathbf{\mu }$是给定的状态向量，${\theta }_t$表示标量漂移系数，$g_t$表示扩散系数。假定${\theta }_t$、$g_t$满足指定关系 $2{\lambda }^2=g_t^2/{\theta }_t$，其中 ${\lambda }^2$是给定的常量标量。因此，其转移概率具有一个封闭形式的解析解：
$$\begin{array}{rl}p(x_t|x_s)& =\mathcal{N}({\bar{m}}_{s:t},{\bar{\sigma }}_{s:t}^{2}I)\\ & =\mathcal{N}\left(\mu +(x_s-\mu )e^{-{\bar{\theta }}_{s:t}},\frac{g_t^2}{2{\theta }_t}\left(1-e^{-2{\bar{\theta }}_{s:t}}\right)I\right),\\ {\bar{\theta }}_{s:t}& ={\int }_s^t{\theta }_{z}dz\end{array}$$
随着时间$t$的推移，整个${\mathbf{X}}_{\mathbf{t}}$会收敛于$\mathcal{N}(\mathbf{\mu },{\lambda }^2)$.

这个是怎么推导的？Yue等人在Appendix C给出了推导，但没有对寻找的辅助函数进行说明。这里给一个证明。
一般地对于随机过程若有：
$$d{X}_t=(A_t{X}_t+B_t)dt+(C_t{X}_t+D_t)d{W}_t$$
有一个本身符合Ito过程的$I_t={\mu }_I(t)dt+{\sigma }_I(t)d{W}_t$，对于$d{Y}_t=d{X}_t{I}_t=I_{t}d{W}_t+W_{t}d{I}_t+d<I,X{>}_t$，$d<I,X{>}_t$为一个二次协变差，其为$({\sigma }_I(t)d{W}_t)(C_t{X}_{t}d{W}_t)={\sigma }_I(t)C_t{X}_{t}dt$，代入到$d{X}_t{I}_t$之中，消除让积分变得困难的随机过程$X_t$，则可以获得对应的$I_t$。

将我们找到的$I(t)$代回到$d{Y}_t$的表达式中。这里你甚至可以不用直接赵$I(t)$，而是找到一个表达式：$(I^{\prime }(t)-I(t){\theta }_t)x_t=0$，可以看到方程大大简化了：
$$d{Y}_t=(I(t){\theta }_t\mu )dt+I(t)g_{t}d{w}_t$$
现在$d{Y}_t$的漂移项和扩散项都只依赖于时间$t$，不依赖于随机过程本身。我们可以直接对两边从$s$到$t$进行积分：
$${\int }_s^{t}d{Y}_z={\int }_s^{t}I(z){\theta }_z\mu dz+{\int }_s^{t}I(z)g_{z}d{w}_z$$
左边等于$Y_t-Y_s$。根据$Y_t$的定义：
$Y_t=I(t){\mathbf{x}}_t=e^{{\bar{\theta }}_t}{\mathbf{x}}_t$
$Y_s=I(s){\mathbf{x}}_s=e^{{\bar{\theta }}_s}{\mathbf{x}}_s={\mathbf{x}}_s$

所以，积分后的方程为：
$e^{{\bar{\theta }}_t}{\mathbf{x}}_t-e^{{\bar{\theta }}_s}{\mathbf{x}}_s=\mathbf{\mu }{\int }_s^t{e}^{{\bar{\theta }}_z}{\theta }_{z}dz+{\int }_s^t{e}^{{\bar{\theta }}_z}{g}_{z}d{\mathbf{w}}_z$

这两个积分里，前者可以直接积分，后者需要使用Ito Isometry，简单来说就是其方差可以直接放在积分里面，推导需要条件期望公式和全方差公式。别忘记$d{\mathbf{w}}_z$本身是一个标准高斯分布，于是：
$$\begin{array}{rl}{\int }_s^t{e}^{{\bar{\theta }}_z}{g}_{z}d{\mathbf{w}}_z& =\mathcal{N}(0,{\int }_s^t{e}^{2{\bar{\theta }}_z}{g}_z^{2}dzI)\\ & =\mathcal{N}(0,{\lambda }^2{\int }_s^t{e}^{2{\bar{\theta }}_z}2{\theta }_{z}dzI)\\ & =\mathcal{N}(0,{\lambda }^2(e^{2{\bar{\theta }}_t}-e^{2{\bar{\theta }}_s})I)\end{array}$$
(5)到(6)是因为用了$2{\lambda }^2=g_t^2/{\theta }_t$，最后放在一起就可以推出(2)-(4)了。

Doob’s h-transform标准形式如下：
$$d{\mathbf{X}}_t=(\mathbf{f}({\mathbf{X}}_t,t)+g_t^2\mathbf{h}({\mathbf{X}}_t,t,{\mathbf{X}}_T,T)dt+g_{t}d{\mathbf{W}}_t,{\mathbf{x}}_0\sim p({\mathbf{x}}_0|{\mathbf{x}}_{\mathbf{T}})$$
Doob变换是一种随机过程里的数学技术。它通过将特定的 h函数纳入随机微分方程（SDE）的漂移项来变换原始过程，使该过程能够通过预定的终点。在漂移项额外加入$\mathbf{h}({\mathbf{X}}_t,t,{\mathbf{X}}_T,T)={\nabla }_{{\mathbf{x}}_{\mathbf{T}}}\log p({\mathbf{x}}_{\mathbf{T}}|{\mathbf{x}}_{\mathbf{t}})$，当$t=T$时，$p({\mathbf{x}}_t|{\mathbf{x}}_0,{\mathbf{x}}_T)=1$

GOUB

Yue等人发现，GOU过程(1)具有均值回归特性，即如果我们将初始状态 $x_0$视为高质量图像，将对应的低质量图像$x_T=\mu$作为最终条件，那么高质量图像将逐渐收敛于一个以低质量图像为均值、方差稳定为${\lambda }^2$的高斯分布。然而，逆向过程的初始状态需要人为地向低质量图像中添加噪声，这会导致一定的信息损失，从而影响性能。巧合的是，Doob’s h-transform可以修改随机微分方程，使其在终端时间 T时通过指定的 $x_T$。因此，需要着重指出的是，将 h -变换应用于GOU过程能有效消除终端噪声的影响，直接在高质量图像和低质量图像之间建立点对点的关系。

前向和反向过程

利用Doob’s h-transform和(2)-(4)，基于GOU这个方程，得到前向过程。
前向过程如下：
$$\begin{array}{c}d{\mathbf{x}}_{\mathbf{t}}=\left({\theta }_t+g_t^2\frac{e^{-2{\bar{\theta }}_{t:T}}}{{\bar{\sigma }}_{t:T}^2}\right)({\mathbf{x}}_T-{\mathbf{x}}_t)dt+g_{t}d{\mathbf{w}}_{\mathbf{t}}.\end{array}$$
其中${\bar{\sigma }}_{t:T}^2={\lambda }^2(1-e^{-2{\bar{\theta }}_{t:T}})$。具体推导比较长，在Yue等人的Appendix A.1里，大概过程是从(2)-(4)写出$p({\mathbf{x}}_t|{\mathbf{x}}_s)$的具体分布，依据${\nabla }_{{\mathbf{x}}_{\mathbf{T}}}\log p({\mathbf{x}}_{\mathbf{T}}|{\mathbf{x}}_{\mathbf{t}})$推导$h$，即可推导(8)，$\mathbf{h}({\mathbf{X}}_t,t,{\mathbf{X}}_T,T)=g_t^2\frac{e^{-2{\bar{\theta }}_{t:T}}}{{\bar{\sigma }}_{t:T}^2}({\mathbf{x}}_T-{\mathbf{x}}_t)$

$p({\mathbf{x}}_t|{\mathbf{x}}_0,{\mathbf{x}}_T)$的推导可以从贝叶斯公式推导。
$$\begin{array}{rl}p({\mathbf{x}}_t|{\mathbf{x}}_0,{\mathbf{x}}_T)& =\mathcal{N}({\bar{\mathbf{m}}}_t^{\prime },{\bar{\sigma }}_t^{\prime 2}\mathbf{I})\\ {\bar{\mathbf{m}}}_t^{\prime }=e^{-{\bar{\theta }}_t}\frac{{\bar{\sigma }}_{t:T}^2}{{\bar{\sigma }}_T^2}{\mathbf{x}}_0& +\left(1-e^{-{\bar{\theta }}_t}\frac{{\bar{\sigma }}_{t:T}^2}{{\bar{\sigma }}_T^2}+e^{-2{\bar{\theta }}_{t:T}}\frac{{\bar{\sigma }}_t^2}{{\bar{\sigma }}_T^2}\right){\mathbf{x}}_T\\ {\bar{\sigma }}_t^{\prime 2}& =\frac{{\bar{\sigma }}_t^2{\bar{\sigma }}_{t:T}^2}{{\bar{\sigma }}^2}\end{array}$$
有了SDE，我们就不用一步一步推导，而是直接一步到位，从${\mathbf{x}}_0,{\mathbf{x}}_T$直接到${\mathbf{x}}_t$，这是训练的第一步。训练的第二步是让模型学习到从${\mathbf{x}}_t$到${\mathbf{x}}_{t-1}$的演化。

反向SDE如下，有着$p({\mathbf{x}}_{\mathbf{t}}|{\mathbf{x}}_{\mathbf{T}})$的边际分布：
$$d{\mathbf{x}}_t=\left[({\theta }_t+g_t^2\frac{e^{-2{\bar{\theta }}_{t:T}}}{{\bar{\sigma }}_{t:T}^2})({\mathbf{x}}_T-{\mathbf{x}}_t)-g_t^2{\nabla }_{{\mathbf{x}}_t}\log p({\mathbf{x}}_t|{\mathbf{x}}_T)\right]dt+g_{t}d{\mathbf{w}}_t$$
并且存在一个概率流常微分方程：
$$d{\mathbf{x}}_t=\left[({\theta }_t+g_t^2\frac{e^{-2{\bar{\theta }}_{t:T}}}{{\bar{\sigma }}_{t:T}^2})({\mathbf{x}}_T-{\mathbf{x}}_t)-\frac{1}{2}{g}_t^2{\nabla }_{{\mathbf{x}}_t}\log p({\mathbf{x}}_t|{\mathbf{x}}_T)\right]dt$$
至于为什么这里ODE变成了$\frac{1}{2}$，有一个性质，为保持边际概率密度不变，这一项就得恰好减半。

损失函数

先回顾一下，依照Score based diffusion model，利用conditional score matching，损失函数如下：
$$L=\frac{1}{2}{\int }_0^T{\mathbb{E}}_{x_t}\left[\lambda (t){\Vert {\nabla }_{x_t}\log p(x_t)-s_{\theta }(x_t,t)\Vert }^2\right]dt\propto \frac{1}{2}{\int }_0^T{\mathbb{E}}_{x_0,x_t}\left[\lambda (t){\Vert {\nabla }_{x_t}\log p(x_t|x_0)-s_{\theta }(x_t,t)\Vert }^2\right]dt$$
其中$\lambda (t)$作为加权函数，若将其选为$g^2(t)$，则能在负对数似然上得到更优的上界（Song等，2021a）。而正比一行实际上是最常用的，因为条件概率$p(x_t|x_0)$通常是可获取的。最终，可以从先验分布 $p(x_T)\approx p_{\text{prior}}(x)$中采样得到 $x_T$，并通过迭代步骤对公式 (2)进行数值求解来得到 $x_0$，从而完成生成过程。

相应地，在GOUB里，得分项${\nabla }_{x_t}\log p({\mathbf{x}}_t|{\mathbf{x}}_T)$可以由神经网络 $s_{\theta }({\mathbf{x}}_t,{\mathbf{x}}_T,t)$进行参数化，并且可以使用上述score matching的损失函数进行估计。不幸的是，对随机微分方程的得分函数进行训练通常是一项重大挑战。作者没有明说，但我想有一个原因很重要，SDE是连续的，训练神经网络是离散的，为此，Yue等人是通过用反向SDE再用Euler Sampling得到的反向离散化的方程。而先前因为GOUB的解析解是知道的，作者于是推出了一个更为稳定的，使用ELBO的损失函数并推导证明之。

假设$x_T$是满足GOU方程的一个有限随机变量，对于固定的 x_T，对数似然函数$E_{p(x_0)}[\log p_{\theta }(x_0|x_T)]$具有一个ELBO：
$$\text{ELBO}={\mathbb{E}}_{p({\mathbf{x}}_0)}\left\{{\mathbb{E}}_{p({\mathbf{x}}_1|{\mathbf{x}}_0)}[\log p_{\mathbf{\theta }}({\mathbf{x}}_0|{\mathbf{x}}_1,{\mathbf{x}}_T)]-\sum _{t=2}^T{\mathbb{E}}_{p({\mathbf{x}}_t|{\mathbf{x}}_0)}[\text{KL}(p({\mathbf{x}}_{t-1}|{\mathbf{x}}_0,{\mathbf{x}}_t,{\mathbf{x}}_T)||p_{\mathbf{\theta }}({\mathbf{x}}_{t-1}|{\mathbf{x}}_t,{\mathbf{x}}_T))]\right\}$$

假设 $p_{\mathbf{\theta }}({\mathbf{x}}_{t-1}|{\mathbf{x}}_t,{\mathbf{x}}_T)$ 是一个具有恒定方差的高斯分布 $\mathcal{N}({\mathbf{\mu }}_{\mathbf{\theta },t-1},{\sigma }_{\mathbf{\theta },t-1}^2\mathbf{I})$，最大化ELBO等价于最小化：
$$L={\mathbb{E}}_{t,{\mathbf{x}}_0,{\mathbf{x}}_t,{\mathbf{x}}_T}\left[\frac{1}{2{\sigma }_{\mathbf{\theta },t-1}^2}\Vert {\mathbf{\mu }}_{t-1}-{\mathbf{\mu }}_{\mathbf{\theta },t-1}{\Vert }^2\right]$$
其中，${\mathbf{\mu }}_{t-1}$ 表示 $p({\mathbf{x}}_{t-1}|{\mathbf{x}}_0,{\mathbf{x}}_t,{\mathbf{x}}_T)$ 的均值：
$${\mu }_{t-1}=\frac{1}{{\bar{\sigma }}_t^{\prime 2}}\left[{\bar{\sigma }}_{t-1}^{\prime 2}(x_t-b{x}_T)a+({\bar{\sigma }}_t^{\prime 2}-{\bar{\sigma }}_{t-1}^{\prime 2}{a}^2){\bar{m}}_t^{\prime }\right]$$
其中，
$$a=e^{-{\bar{\theta }}_{t-1:t}}\frac{{\bar{\sigma }}_{t:T}^2}{{\bar{\sigma }}_{t-1:T}^2}$$
$$b=\frac{1}{{\bar{\sigma }}_T^2}\left\{(1-e^{-{\bar{\theta }}_t}){\bar{\sigma }}_{t:T}^2+e^{-2{\bar{\theta }}_{t:T}}{\bar{\sigma }}_t^2-\left[(1-e^{-{\bar{\theta }}_{t-1}}){\bar{\sigma }}_{t-1:T}^2+e^{-2{\bar{\theta }}_{t-1:T}}{\bar{\sigma }}_{t-1}^2\right]a\right\}$$

这个证明就比较多，感兴趣的可以参考参考文献第二篇。

根据反向SDE方程，离散化：
$${\mathbf{x}}_{t-1}={\mathbf{x}}_t-\left({\theta }_t+g_t^2\frac{e^{-2{\bar{\theta }}_{t:T}}}{{\bar{\sigma }}_{t:T}^2}\right)({\mathbf{x}}_T-{\mathbf{x}}_t)+g_t^2{\nabla }_{{\mathbf{x}}_t}\log p({\mathbf{x}}_t|{\mathbf{x}}_T)-g_t{\mathbf{ϵ}}_t$$
其中，${\mathbf{ϵ}}_t\sim \mathcal{N}(0,d_t\mathbf{I})$。
因此：
$${\mathbf{\mu }}_{\theta ,t-1}={\mathbf{x}}_t-\left({\theta }_t+g_t^2\frac{e^{-2{\bar{\theta }}_{t:T}}}{{\bar{\sigma }}_{t:T}^2}\right)({\mathbf{x}}_T-{\mathbf{x}}_t)+g_t^2{\nabla }_{{\mathbf{x}}_t}\log p_{\theta }({\mathbf{x}}_t|{\mathbf{x}}_T)$$
标准差就是：${\sigma }_{\theta ,t-1}=g_t$.
作者发现，L1范数损失在图像重构的结果上效果更好，故而采用L1范数，最后的损失函数结果太长就不写了，代入上面的结果即可。最后，如果我们得到最优的 ${\mathbf{ϵ}}_{\mathbf{\theta }}^{\ast }({\mathbf{x}}_t,{\mathbf{x}}_T,t)$，就可以计算反向过程的得分 ${\nabla }_{{\mathbf{x}}_t}\log p({\mathbf{x}}_t|{\mathbf{x}}_T)\approx \frac{-{\mathbf{ϵ}}_{\mathbf{\theta }}^{\ast }({\mathbf{x}}_t,{\mathbf{x}}_T,t)}{{\bar{\sigma }}_t^{\prime }}$，直接代入即可。

Mean-ODE

与普通的扩散模型不同，作者表示，对均值 ${\mu }_{\theta ,t-1}$ 的参数化是从随机微分方程的微分推导而来的，这有效地结合了离散扩散模型和基于连续分数的生成模型的特点。在反向过程中，每个采样步骤的值在训练期间会逼近真实均值。因此，作者提出了一个Mean - ODE模型，该模型省略了布朗漂移项，也就是直接在反向SDE上，从经验和实验结果的表现证明上直接删除了$d{\mathbf{W}}_{\mathbf{t}}$：
$$d{\mathbf{x}}_t=\left[{\theta }_t+g_t^2\frac{e^{-2{\bar{\theta }}_{t:T}}}{{\bar{\sigma }}_{t:T}^2}({\mathbf{x}}_T-{\mathbf{x}}_t)-g_t^2{\nabla }_{{\mathbf{x}}_t}\log p({\mathbf{x}}_t|{\mathbf{x}}_T)\right]dt(9)$$
作者在实验中也发现，Mean-ODE的表现比Score-ODE好。

UniDB

UniDB仅在GOUB代码的基础上做了极少的修改，而且也利用stochastic optimal control在数学上提供了diffusion bridge via Doob’s h-transform的情况的理解，也证明了这是UniDB的$\gamma \to \infty$的一种特殊情况，在超分辨率（DIV2K）、图像修复（CelebA - HQ）和去雨（Rain100H）上都表现到了SOTA级别。

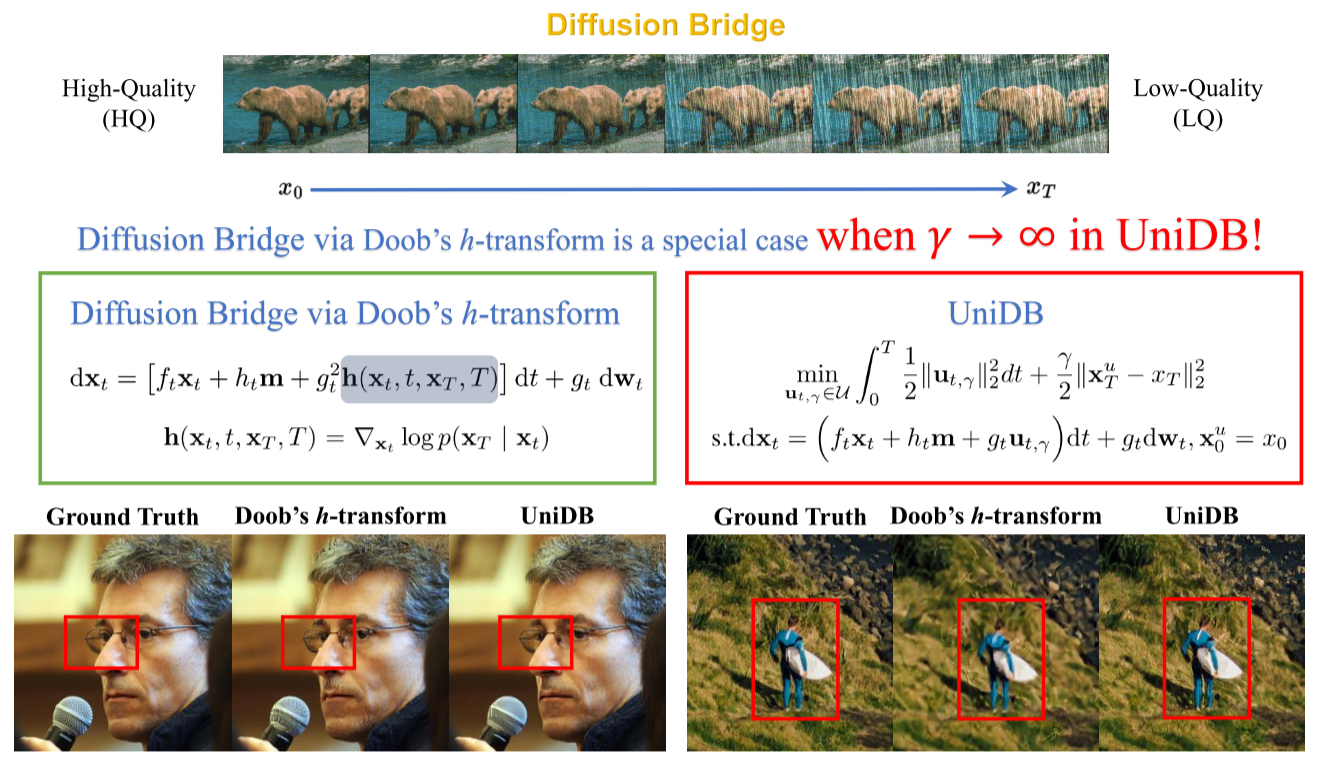
UniDB指出，GOUB其核心技术Doob’s h-transform是一种次优解。而且GOUB虽然性能好，但也有内在的细节模糊或扭曲问题，并通过理论实验帮助阐释了这一点。不过UniDB和GOUB都有着采样慢的通病，但我认为两者的采样速度不会有多少差距，UniDB是可以做到即插即用的，只在GOUB上做了极少量的修改，起到了统一和更深的insight。

注意到图上右边s.t.的部分，$f_t{\mathbf{x}}_{\mathbf{t}}$是drift项没错，不过多了一个$h_t\mathbf{m}$，$\mathbf{m}$是一个given state，一个给定的状态，比如${\mathbf{x}}_{\mathbf{t}-1}$或者别的。’
把之前GOUB的漂移项展开：
$${\theta }_t(\mathbf{\mu }-x_t)={\theta }_t\mathbf{\mu }-{\theta }_t{x}_t$$
然后再看UniDB的通用漂移项：
$$f_t{x}_t+h_t\mathbf{m}$$
只要进行如下的参数代换，两者就完全等价了：

• 令 $f_t=-{\theta }_t$
• 令 $h_t={\theta }_t$
• 令 $\mathbf{m}=\mathbf{\mu }$

这也是原文中提到的，还有VE,VP等。

UniDB中的一些proposition和GOUB很相似，这里阐述一下不同的部分。

1. 依据Theorem 4.1，可以得到一个从$x_0$连接到终端$x_T$邻域的最优控制正向随机微分方程，这个${\mathbf{u}}_{t,\gamma }^{\ast }$也是可以计算的，与$\mathbf{m},{\mathbf{x}}_{\mathbf{t}},{\mathbf{x}}_{\mathbf{T}}$有关，正向过程中$x_t$的转移情况也可以推出。
2. 对于SOC问题，当$\gamma \to \infty$时，最优控制器变为 $u_{t,\infty }^{\ast }=g_t{\nabla }_{{\mathbf{x}}_t}\log p({\mathbf{x}}_T|{\mathbf{x}}_t)$，并且对应于线性随机微分方程形式的前向和后向随机微分方程与 Doob 的 $h$-变换相同。
3. 记$\mathcal{J}({\mathbf{u}}_{t,\gamma },\gamma )\triangleq {\int }_0^T\frac{1}{2}\Vert {\mathbf{u}}_{t,\gamma }{\Vert }_2^2\mathrm{d}t+\frac{\gamma }{2}\Vert {\mathbf{x}}_T^u-x_T{\Vert }_2^2$为系统的总成本，$u_{t,\gamma }^{\ast }$为最优控制器，则有$\mathcal{J}({\mathbf{u}}_{t,\gamma }^{\ast },\gamma )\le \mathcal{J}({\mathbf{u}}_{t,\infty }^{\ast },\infty )$，这说明$\gamma \to \infty$的情况并非是最优解，后面作者根据实验发现$\gamma$的取值是随着不同的具体任务而有变化的。
4. 记初始状态分布为 $x_0$，由控制器产生的终端分布为 ${\mathbf{x}}_T^u$，以及预先定义的终端分布为 $x_T$，则
   $$\Vert {\mathbf{x}}_T^u-x_T{\Vert }_2^2=\frac{e^{-2{\bar{\theta }}_T}}{(1+\gamma {\lambda }^2(1-e^{-2{\bar{\theta }}_T}){)}^2}\Vert x_T-x_0{\Vert }_2^2$$
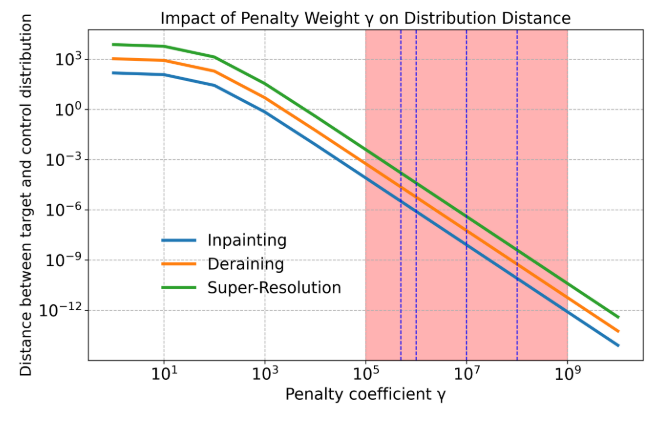
   这说明控制的终点和实际的终点是受到$\gamma$的调控的，如下图，红色区域是作者推荐的关注区域，蓝色点竖线是作者在后面的消融实验中的选取方式，在四倍超分，图像修复，去雨三个任务上，从PSNR,SSIM,LPIPS,FIDS四个指标看，$\gamma$的不同，分数也不同，而且同一个任务里也可能并非一个gamma能得到四个指标都有良好的结果。
   

与之前GOUB的类似，反向过程SDE和Mean-ODE如下：
$$\mathrm{d}{\mathbf{x}}_t=[f_t{\mathbf{x}}_t+h_t\mathbf{m}+g_t{\mathbf{u}}_{t,\gamma }^{\ast }-g_t^2{\nabla }_{{\mathbf{x}}_t}\log p({\mathbf{x}}_t|x_T)]\mathrm{d}t+g_t\mathrm{d}{\tilde{\mathbf{w}}}_t$$
$$\mathrm{d}{\mathbf{x}}_t=[f_t{\mathbf{x}}_t+h_t\mathbf{m}+g_t{\mathbf{u}}_{t,\gamma }^{\ast }-g_t^2{\nabla }_{{\mathbf{x}}_t}\log p({\mathbf{x}}_t|x_T)]\mathrm{d}t$$

整个训练中，以GOU为例子，项的差距与GOUB差距很小，可以看到几乎只是${\gamma }^{-1}$的引入：
$$e^{-{\bar{\theta }}_t}\frac{{\bar{\sigma }}_{t:T}^2}{{\bar{\sigma }}_T^2}\Rightarrow e^{-{\bar{\theta }}_t}\frac{{\gamma }^{-1}+{\bar{\sigma }}_{t:T}^2}{{\gamma }^{-1}+{\bar{\sigma }}_T^2}$$
$$\underset{\text{GOUB}}{\underbrace{g_t\mathbf{h}=\frac{g_t{e}^{-2{\bar{\theta }}_{t:T}}(x_T-{\mathbf{x}}_t)}{{\bar{\sigma }}_{t:T}^2}}}\Rightarrow \underset{\text{UniDB-GOU}}{\underbrace{{\mathbf{u}}_{t,\gamma }^{\ast }=\frac{g_t{e}^{-2{\bar{\theta }}_{t:T}}(x_T-{\mathbf{x}}_t)}{{\gamma }^{-1}+{\bar{\sigma }}_{t:T}^2}}}$$
下面是两个算法。算法一的思路就是，先随机抽取一对图像$({\mathbf{x}}_0,{\mathbf{x}}_{\mathbf{t}})$，然后在Uniform{1,…,T}Uniform\{1,\dots,T\}Uniform{1,…,T}抽取一个$t$，计算${\bar{\mathbf{\mu }}}_{t,\gamma },\gamma ,{\bar{\sigma }}_t^{\prime 2}$。为训练稳定，不直接预测分数，而是依据分数匹配理论，分数函数可以被参数化为：
$${\nabla }_{x_t}\log p(x_t|x_T)\approx -\frac{{ϵ}_{\theta }(x_t,x_T,t)}{{\bar{\sigma }}_t^{\prime }}$$
通过计算${\bar{\mathbf{\mu }}}_{t-1,\theta }$，再计算${\bar{\mathbf{\mu }}}_{t-1,\gamma }$，计算损失函数梯度，让算法收敛。整个算法其实和之前计算GOUB的${\mathbf{\mu }}_{\theta ,t-1}$和${\mathbf{\mu }}_{t-1}$挺像的。

算法二就是采样啦，解决新问题。

写到这里

参考文献

Zhu K, Pan M, Ma Y, et al. UniDB: A Unified Diffusion Bridge Framework via Stochastic Optimal Control[J]. arXiv preprint arXiv:2502.05749, 2025.
Yue C, Peng Z, Ma J, et al. Image restoration through generalized ornstein-uhlenbeck bridge[J]. arXiv preprint arXiv:2312.10299, 2023.