数据结构:集合操作(Set Operations): 并集(Union)、交集(Intersection)、 差集(Difference)
目录
并集(Union)A ∪ B
未排序数组的并集
已排序数组的并集
交集(Intersection) A ∩ B
未排序数组的交集
已排序数组的交集
差集(Difference)A - B
未排序数组的差集
已排序数组的差集
并集(Union)A ∪ B
给定两个数组 A 和 B,求一个数组 C,其中包含 A 和 B 的所有元素,不重复。
未排序数组的并集
我们现在处理的是 两个未排序数组 A 和 B 的并集,将它们的所有 不重复元素 放入数组 C 中。
输入:A = {3, 5, 10, 4, 6} (长度 m = 5)B = {12, 4, 7, 2, 5} (长度 n = 5)期望输出 C:C = {3, 5, 10, 4, 6, 12, 7, 2}
🧠 算法分解
步骤一:创建一个结果数组 C,长度最大是 m+n(极限情况下所有元素都不同)
int C[m + n]; // 最多 m+n 个不重复元素
int k = 0; // C 的当前长度
步骤二:把 A 中的所有元素直接复制到 C
for (int i = 0; i < m; i++) {C[k++] = A[i];
}
此时 C 中已经有 A 的全部元素,长度为 m。
步骤三:遍历 B 中的每个元素,逐个与 C 中已有元素比较,若不存在,则添加
for (int i = 0; i < n; i++) {bool found = false;for (int j = 0; j < k; j++) {if (B[i] == C[j]) {found = true;break;}}if (!found) {C[k++] = B[i];}
}
完整代码
#include <iostream>
using namespace std;int main() {int A[] = {3, 5, 10, 4, 6};int B[] = {12, 4, 7, 2, 5};int m = 5, n = 5;int C[100]; // 足够大,防止越界int k = 0; // 当前C的长度// Step 1: 复制A到Cfor (int i = 0; i < m; i++) {C[k++] = A[i];}// Step 2: 将B中不在C中的元素添加进Cfor (int i = 0; i < n; i++) {bool found = false;for (int j = 0; j < k; j++) {if (B[i] == C[j]) {found = true;break;}}if (!found) {C[k++] = B[i];}}// 输出结果cout << "并集 C = ";for (int i = 0; i < k; i++) {cout << C[i] << " ";}cout << endl;return 0;
}
📊 时间复杂度分析
我们来逐步分析每一部分的时间消耗:
步骤一:复制 A 中所有元素到 C
for (int i = 0; i < m; i++)C[k++] = A[i];
-
时间复杂度 = O(m)
-
每个元素复制一次,共 m 次操作。
步骤二:检查 B 中的每个元素是否已在 C 中
for (int i = 0; i < n; i++) {for (int j = 0; j < k; j++) {...}
}
-
最坏情况:B 中所有元素都不在 A 中
-
每添加一个元素,
k会增加 -
所以:
-
第1个 B 元素最多比较 m 次
-
第2个 B 元素最多比较 m+1 次
-
...
-
第n个 B 元素最多比较 m + n − 1 次
-
这是一个等差数列求和问题:
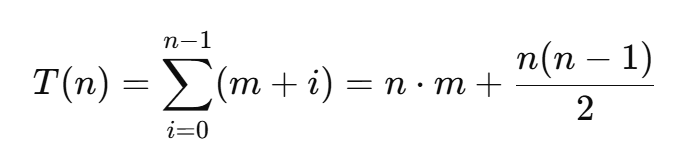
因此,总时间复杂度 = O(m + n×m + n²) = O(n² + n×m) = O( n^2 )
空间复杂度分析:
-
使用了一个新数组 C,其最大长度为
m + n -
空间复杂度 = O(m + n)
已排序数组的并集
给定两个升序排序数组 A 和 B,构造一个新数组 C,包含它们的所有元素(不重复)。
-
输入:
-
排序数组 A,长度 m
-
排序数组 B,长度 n
-
-
输出:
-
新数组 C,其中包含 A 和 B 的所有元素,不重复,且仍为升序。
-
问题特点
-
输入数组 已经排序 ⇒ 可以用“双指针法”快速处理
-
输出结果数组需要 去重
🧠 核心思路:双指针合并 + 去重
我们借助两个指针 i 和 j 分别指向数组 A 和 B 的当前元素,用一个结果指针 k 构建 C。
🔹 Step 1:初始化
int i = 0, j = 0, k = 0;
🔹 Step 2:主循环,遍历 A 和 B,直到有一个数组走完
while (i < m && j < n) {...
}
我们在循环中对比 A[i] 和 B[j]:
✅ 情况一:A[i] < B[j]
说明 A[i] 较小,可以直接放进 C。别忘了先检查是否重复:
if (k == 0 || C[k - 1] != A[i]) {C[k++] = A[i];
}
i++;
✅ 情况二:A[i] > B[j]
说明 B[j] 较小,处理逻辑与上面一样:
if (k == 0 || C[k - 1] != B[j]) {C[k++] = B[j];
}
j++;
✅ 情况三:A[i] == B[j]
两数组当前元素相同 → 只加入一个,跳过重复:
if (k == 0 || C[k - 1] != A[i]) {C[k++] = A[i];
}
i++;
j++;
🔹 Step 3:处理剩下的 A 或 B 的元素
可能其中一个数组还有剩余未处理的元素,需要单独补上(仍然要去重):
while (i < m) {if (k == 0 || C[k - 1] != A[i])C[k++] = A[i];i++;
}while (j < n) {if (k == 0 || C[k - 1] != B[j])C[k++] = B[j];j++;
}
完整代码
#include <iostream>
using namespace std;void unionSorted(int A[], int m, int B[], int n) {int C[200]; // 结果数组 Cint i = 0, j = 0, k = 0; // 指针初始化// 主循环:合并两个已排序数组while (i < m && j < n) {if (A[i] < B[j]) {if (k == 0 || C[k - 1] != A[i])C[k++] = A[i];i++;}else if (A[i] > B[j]) {if (k == 0 || C[k - 1] != B[j])C[k++] = B[j];j++;}else { // A[i] == B[j]if (k == 0 || C[k - 1] != A[i])C[k++] = A[i];i++;j++;}}// 处理 A 剩余部分while (i < m) {if (k == 0 || C[k - 1] != A[i])C[k++] = A[i];i++;}// 处理 B 剩余部分while (j < n) {if (k == 0 || C[k - 1] != B[j])C[k++] = B[j];j++;}// 输出并集结果cout << "并集 C = ";for (int p = 0; p < k; p++) {cout << C[p] << " ";}cout << endl;
}int main() {int A[] = {1, 3, 5, 7};int B[] = {2, 3, 5, 6, 8};int m = sizeof(A) / sizeof(A[0]);int n = sizeof(B) / sizeof(B[0]);unionSorted(A, m, B, n);return 0;
}
模拟过程
A = {1, 3, 5, 7}
B = {2, 3, 5, 6, 8}
| A[i] | B[j] | 比较结果 | 插入C | C数组状态 |
|---|---|---|---|---|
| 1 | 2 | A < B | 1 | {1} |
| 3 | 2 | A > B | 2 | {1, 2} |
| 3 | 3 | A == B | 3 | {1, 2, 3} |
| 5 | 5 | A == B | 5 | {1, 2, 3, 5} |
| 7 | 6 | A > B | 6 | {1, 2, 3, 5, 6} |
| 7 | 8 | A < B | 7 | {1, 2, 3, 5, 6, 7} |
| - | 8 | A 完了 | 8 | {1, 2, 3, 5, 6, 7, 8} |
📊 时间复杂度:
-
每次迭代最多移动一次指针 i 或 j → 总最多 m+n 次操作
-
去重检查仅需
C[k - 1],时间为 O(1)
总时间复杂度 = O(m + n)
空间复杂度:
-
新数组 C 最多 m + n 个元素
-
空间复杂度 = O(m + n)
交集(Intersection) A ∩ B
未排序数组的交集
目标: 从两个无序数组 A 和 B 中找出共同存在的元素(不重复),保存到数组 C。
❗️问题特点:
-
无序数组:不能使用排序、二分、双指针等优化技巧。
-
只能使用逐一比较(暴力匹配)。
-
为避免重复,必须手动检查结果数组 C 中是否已经包含某个元素。
🧠 核心思路
我们采用一个构造式方法来思考交集,步骤如下:
步骤 1:初始化辅助数组
-
创建结果数组
C[m + n],足够大 -
设置变量
k = 0表示结果数组长度
int C[m + n];
int k = 0;
步骤 2:遍历 A 中的每个元素
for (int i = 0; i < m; i++) {...
}
我们要判断 A[i] 是否也出现在 B 中。
步骤 3:对每个 A[i],检查它是否存在于 B 中
这是通过一个内层循环完成的:
bool found_in_B = false;
for (int j = 0; j < n; j++) {if (A[i] == B[j]) {found_in_B = true;break;}
}
步骤 4:如果 A[i] 在 B 中,还要检查是否已添加到 C
避免重复添加元素,使用一个辅助函数:
bool existsInC = false;
for (int x = 0; x < k; x++) {if (C[x] == A[i]) {existsInC = true;break;}
}
步骤 5:如果 A[i] 在 B 中,且未在 C 中,添加到结果数组
if (found_in_B && !existsInC) {C[k++] = A[i];
}
完整代码实现
#include <iostream>
using namespace std;// 判断一个元素是否存在于数组中
bool exists(int arr[], int size, int val) {for (int i = 0; i < size; i++) {if (arr[i] == val)return true;}return false;
}// 求未排序数组交集
void intersectionUnsorted(int A[], int m, int B[], int n) {int C[100]; // 假设最大100个交集元素int k = 0;for (int i = 0; i < m; i++) {// 判断 A[i] 是否存在于 Bbool foundInB = false;for (int j = 0; j < n; j++) {if (A[i] == B[j]) {foundInB = true;break;}}// 如果在B中,且不在C中,加入Cif (foundInB && !exists(C, k, A[i])) {C[k++] = A[i];}}// 输出交集结果cout << "交集 A ∩ B = ";for (int i = 0; i < k; i++) {cout << C[i] << " ";}cout << endl;
}int main() {int A[] = {3, 5, 10, 4, 6};int B[] = {12, 4, 7, 2, 5};int m = sizeof(A) / sizeof(A[0]);int n = sizeof(B) / sizeof(B[0]);intersectionUnsorted(A, m, B, n);return 0;
}
模拟过程
A = {3, 5, 10, 4, 6};
B = {12, 4, 7, 2, 5};
我们按顺序处理每个 A[i]:
| A[i] | 是否在B中 | 是否已在C中 | 是否加入C | C数组内容 |
|---|---|---|---|---|
| 3 | 否 | - | 否 | |
| 5 | 是 | 否 | ✔ | {5} |
| 10 | 否 | - | 否 | {5} |
| 4 | 是 | 否 | ✔ | {5, 4} |
| 6 | 否 | - | 否 | {5, 4} |
📊 复杂度分析
✅ 时间复杂度
我们有两个嵌套循环:
-
外层:遍历 A → O(m)
-
内层:查找 A[i] 是否在 B → O(n)
-
再加一次遍历 C → 最坏 O(m)
总复杂度为:
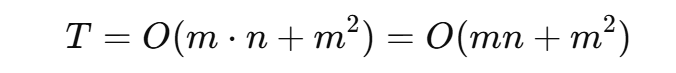
若 m ≈ n,则为 O(n²),属于平方级别的暴力方法。
✅ 空间复杂度
-
新建一个结果数组 C,最多 m 个元素
-
空间复杂度 = O(m)
已排序数组的交集
给定两个 已排序数组 A 和 B,我们要找出它们的交集,即那些同时出现在 A 和 B 中的元素(不重复),并保存在一个新数组 C 中。
-
输入:
-
A[] = 已排序数组,长度为 m
-
B[] = 已排序数组,长度为 n
-
-
输出:
-
C[] = 存储 A 和 B 中都出现的元素,不重复
-
📌 特点
-
数组是 已排序的
-
可以使用“双指针法”进行高效遍历(参考合并数组:数据结构:数组:合并数组(Merging Arrays)-CSDN博客)
-
相同的元素只取一次,不重复添加
🧠 核心思路:双指针扫描
我们使用两个下标 i 和 j:
-
i指向数组 A 的当前位置 -
j指向数组 B 的当前位置
我们从头遍历两个数组,逐步比较当前指向的元素:
步骤流程如下:
-
初始化 i = 0,j = 0,k = 0(k 是结果数组 C 的长度)
-
当 i < m 且 j < n 时:
-
若 A[i] < B[j]:说明 A[i] 小于 B[j],A[i] 不可能是交集元素 →
i++ -
若 A[i] > B[j]:说明 B[j] 小于 A[i],B[j] 不可能是交集元素 →
j++ -
若 A[i] == B[j]:
-
检查是否已添加过该元素(去重)
-
如果没添加过,加入到 C[k++],然后
i++,j++
-
-
-
循环结束,C 就是交集结果
模拟过程
A = {2, 4, 6, 8, 10}
B = {4, 6, 8, 12, 14}
我们用两个指针逐步比对:
| i | j | A[i] | B[j] | 比较结果 | C |
|---|---|---|---|---|---|
| 0 | 0 | 2 | 4 | 2 < 4 → i++ | |
| 1 | 0 | 4 | 4 | 相等 → 加入4 | C = {4} |
| 2 | 1 | 6 | 6 | 相等 → 加入6 | C = {4, 6} |
| 3 | 2 | 8 | 8 | 相等 → 加入8 | C = {4, 6, 8} |
| 4 | 3 | 10 | 12 | 10 < 12 → i++ | |
| 5 | 3 | — | — | i >= m → 结束 |
最终结果:C = {4, 6, 8}
💡 代码实现
🔹 步骤1:定义函数 intersectionSorted()
void intersectionSorted(int A[], int m, int B[], int n) {int C[100]; // 足够大的数组int i = 0, j = 0, k = 0;}🔹 步骤 2:开始主循环,条件是两个指针都没越界
while (i < m && j < n) {...
}
🔹 情况 A:A[i] < B[j]
说明当前 A[i] 比 B[j] 小,因此不可能等于 B 中任何剩下的元素。
我们可以跳过 A[i]:
if (A[i] < B[j]) {i++;
}
🔹 情况 B:A[i] > B[j]
同理,B[j] 更小,也不可能出现在 A 后面,所以跳过 B[j]:
else if (A[i] > B[j]) {j++;
}
🔹 情况 C:A[i] == B[j]
找到了一个交集元素!
但我们还需要 去重,也就是防止重复元素写入 C。
else {if (k == 0 || C[k - 1] != A[i]) {C[k++] = A[i]; // 添加到交集结果数组 C 中}i++;j++;
}
说明:
-
k == 0:是第一个元素,直接添加 -
C[k - 1] != A[i]:当前值没重复才添加
🔹 步骤 3:循环结束,交集数组 C 已完成
你可以用一个循环输出 C:
for (int p = 0; p < k; p++) {cout << C[p] << " ";
}
完整代码
#include <iostream>
using namespace std;void intersectionSorted(int A[], int m, int B[], int n) {int C[100]; // 足够大的数组int i = 0, j = 0, k = 0;while (i < m && j < n) {if (A[i] < B[j]) {i++; // A[i] 小了,不可能在交集中}else if (A[i] > B[j]) {j++; // B[j] 小了,也不在交集中}else {// 元素相等,可能是交集,但要去重if (k == 0 || C[k - 1] != A[i]) {C[k++] = A[i]; // 添加到结果数组}i++;j++;}}// 输出结果数组 Ccout << "交集 C = ";for (int p = 0; p < k; p++) {cout << C[p] << " ";}cout << endl;
}
📊 算法复杂度分析
时间复杂度:
使用的是 双指针遍历:
-
每次最多移动 i 或 j 中的一个
-
最多移动 m + n 次
时间复杂度 = O(m + n),这是最优的方式之一,适用于已排序数组。
空间复杂度:
-
使用了一个新数组 C,最多 m+n 个元素(极限情况是 A 和 B 完全相同)
-
但实际上,交集最多是 min(m, n)
空间复杂度 = O(min(m, n))
差集(Difference)A - B
差集 A - B 表示:在数组 A 中出现,但在数组 B 中没有出现的所有元素(去重),存入数组 C。
未排序数组的差集
问题定义
-
输入:
-
无序数组 A(长度 m)
-
无序数组 B(长度 n)
-
-
输出:
-
数组 C:A 中存在但 B 中没有的所有元素(不重复)
-
🧠 差集本质分析(以 A - B 为例)
对于 A 中的每个元素:
-
判断它是否出现在 B 中
-
如果 没有出现在 B 中,再判断它是否已经加入过 C(避免重复)
-
满足条件 → 加入 C
🪜 算法步骤
🔹 Step 1:初始化结果数组 C
int C[m]; // 最多 m 个差集元素
int k = 0; // 当前结果长度
🔹 Step 2:遍历 A 中的每个元素
for (int i = 0; i < m; i++) {...
}
🔹 Step 3:判断 A[i] 是否在 B 中出现
bool foundInB = false;
for (int j = 0; j < n; j++) {if (A[i] == B[j]) {foundInB = true;break;}
}
🔹 Step 4:若 A[i] 不在 B 中,还需判断是否已加入 C
bool existsInC = false;
for (int x = 0; x < k; x++) {if (C[x] == A[i]) {existsInC = true;break;}
}
🔹 Step 5:满足条件,加入结果数组 C
if (!foundInB && !existsInC) {C[k++] = A[i];
}
完整代码实现
#include <iostream>
using namespace std;// 判断某个值是否在数组中
bool exists(int arr[], int size, int val) {for (int i = 0; i < size; i++) {if (arr[i] == val)return true;}return false;
}// 求未排序数组的差集 A - B
void differenceUnsorted(int A[], int m, int B[], int n) {int C[100]; // 差集结果数组int k = 0;for (int i = 0; i < m; i++) {bool foundInB = false;// 检查 A[i] 是否出现在 B 中for (int j = 0; j < n; j++) {if (A[i] == B[j]) {foundInB = true;break;}}// 如果不在 B 中,且还没加入过 Cif (!foundInB && !exists(C, k, A[i])) {C[k++] = A[i];}}// 输出结果cout << "差集 A - B = ";for (int i = 0; i < k; i++) {cout << C[i] << " ";}cout << endl;
}int main() {int A[] = {3, 5, 10, 4, 6};int B[] = {12, 4, 7, 2, 5};int m = sizeof(A) / sizeof(A[0]);int n = sizeof(B) / sizeof(B[0]);differenceUnsorted(A, m, B, n);return 0;
}
🔁 模拟过程
A = {3, 5, 10, 4, 6};
B = {12, 4, 7, 2, 5};
| A[i] | 是否在B中 | 是否在C中 | 是否加入C | C内容 |
|---|---|---|---|---|
| 3 | 否 | 否 | ✔ | {3} |
| 5 | 是 | - | ✘ | {3} |
| 10 | 否 | 否 | ✔ | {3, 10} |
| 4 | 是 | - | ✘ | {3, 10} |
| 6 | 否 | 否 | ✔ | {3, 10, 6} |
📊 时间复杂度分析
✅ 时间复杂度:
我们有三层循环:
-
外层遍历 A:O(m)
-
内层查找是否在 B 中:O(n)
-
再查一遍是否在 C 中:最坏 O(m)
所以:
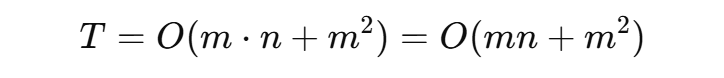
若 m ≈ n ⇒ 最坏为 O(n²),为暴力算法
✅ 空间复杂度:
-
新数组 C,最多 m 个元素
-
空间复杂度 = O(m)
已排序数组的差集
输入特点:
-
两个数组 A 和 B 都是升序排列
-
可以使用 双指针法 高效比较
🧠 思路分析:双指针遍历差集 A - B
使用两个指针:
-
i遍历数组 A(长度 m) -
j遍历数组 B(长度 n) -
k指向结果数组 C 的当前位置
🪜 步骤讲解
🔹 Step 1:初始化指针
int i = 0, j = 0, k = 0;
🔹 Step 2:同时遍历两个数组,判断 A[i] 是否在 B 中
while (i < m && j < n) {...
}
✅ 情况 1:A[i] < B[j]
说明 A[i] 小于 B[j],它不可能在 B 中出现 → A[i] 应该加入差集 C
if (k == 0 || C[k - 1] != A[i])C[k++] = A[i];
i++;
✅ 情况 2:A[i] > B[j]
说明 B[j] 小于 A[i],还不能判断 A[i] 是否在 B 中,需要继续推进 j
j++;
✅ 情况 3:A[i] == B[j]
说明这个元素在 A 和 B 中都有 → 不应加入差集 → 同时跳过 A[i] 和 B[j]
i++;
j++;
🔹 Step 3:处理 A 剩下的元素(B 已走完)
while (i < m) {if (k == 0 || C[k - 1] != A[i])C[k++] = A[i];i++;
}
完整代码实现
#include <iostream>
using namespace std;void differenceSorted(int A[], int m, int B[], int n) {int C[100]; // 结果数组 Cint i = 0, j = 0, k = 0;while (i < m && j < n) {if (A[i] < B[j]) {if (k == 0 || C[k - 1] != A[i])C[k++] = A[i];i++;}else if (A[i] > B[j]) {j++;}else { // A[i] == B[j]i++;j++;}}// 把 A 中剩余未处理的元素加入 Cwhile (i < m) {if (k == 0 || C[k - 1] != A[i])C[k++] = A[i];i++;}// 输出差集结果cout << "差集 A - B = ";for (int p = 0; p < k; p++) {cout << C[p] << " ";}cout << endl;
}int main() {int A[] = {2, 4, 6, 8, 10};int B[] = {4, 6, 12};int m = sizeof(A) / sizeof(A[0]);int n = sizeof(B) / sizeof(B[0]);differenceSorted(A, m, B, n);return 0;
}
🔁 示例模拟
A = {2, 4, 6, 8, 10}
B = {4, 6, 12}
| i | j | A[i] | B[j] | 比较结果 | 加入C | C数组内容 |
|---|---|---|---|---|---|---|
| 0 | 0 | 2 | 4 | A[i] < B[j] | ✔ | {2} |
| 1 | 0 | 4 | 4 | 相等 | ✘ | {2} |
| 2 | 1 | 6 | 6 | 相等 | ✘ | {2} |
| 3 | 2 | 8 | 12 | A[i] < B[j] | ✔ | {2, 8} |
| 4 | 2 | 10 | 12 | A[i] < B[j] | ✔ | {2, 8, 10} |
| 5 | - | - | - | i >= m,结束 |
📊 复杂度分析
✅ 时间复杂度:
-
双指针最多移动 m+n 次
-
每次处理最多一次操作(比较/复制)
总时间复杂度:O(m + n)
✅ 空间复杂度:
-
新数组 C 最多 m 个元素(全部保留的极端情况)
-
空间复杂度 = O(m)
