聚类算法原理与应用(一)：K-means聚类算法原理

聚类

聚类，就是将一个数据集中具有相似特征的数据自动归类到一起，例如柯基犬，金毛犬，哈士奇等不同的犬种都具有犬科的特征，所以可以统一归为狗的一类，而蓝猫，缅因，暹罗等不同的猫也都具有猫科的特征，所以都可以归为狗的一类。

在聚类中每一个猫，狗这样的一个大类称为一个簇(cluster)，簇内的对象越相似，聚类的效果越好，它是一种无监督的学习(Unsupervised Learning)方法。

聚类与分类最大的区别就是分类的目标事先已知。例如猫狗识别，在分类之前已经知道要将它分为猫、狗两个种类；而在聚类中目标是未知的，同样以动物为例，对于一个动物集来说，你并不清楚这个数据集内部有多少种类的动物，你能做的只是利用数据去找到相似的特征，然后根据特征将数据集分为多类，然后人为给出这个聚类结果的定义（即簇识别）。例如，你将一个动物集进行聚类，最终可能根据翅膀的特征分为两个簇（类），起名为有翅膀的动物和没有翅膀的动物；也可能根据更细致的特征分为了五簇（类），然后通过观察这五类动物的特征，你为每一个簇起一个名字，如大象、狗、猫，鸡，鱼等，这就是聚类的基本思想。

K-Means 算法

簇和质心

上面介绍到聚类是将相似的对象归为一个类，聚类算法中称为一簇。K-Means之所以称为K-均值，其中的K就是结果中簇的个数，它是一个超参数，需要人为输入来确定。每个簇对应的中心位置称为质心，一般是通过计算簇中所有数据的均值来确定的。

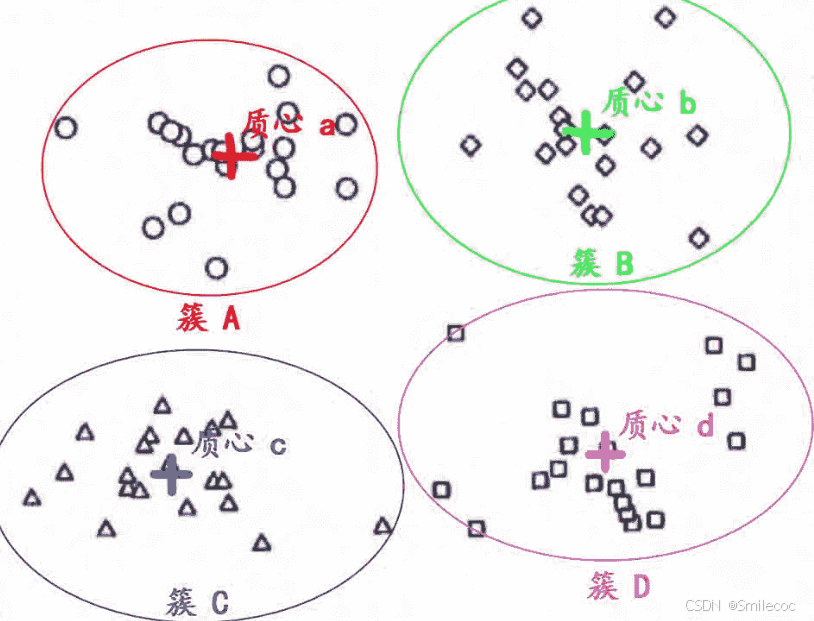
那么如何界定“相似”这一概念呢？在K-Means 算法中是利用距离这个评价标准来量化衡量的，我们通过计算对象与对象之间的距离远近来判断，距离较近的点就是相似的。在K-Means中使用的是欧式距离，可以理解为直线距离。
二维情况下两点的欧式距离为：
$$d(A,B)=\sqrt{(x_2-x_1{)}^2+(y_2-y_1{)}^2}$$
多维情况下距离如下：
$$d(A,B)=\sqrt{(x_2-x_1{)}^2+(y_2-y_1{)}^2+\cdots +(z_2-z_1{)}^2}$$

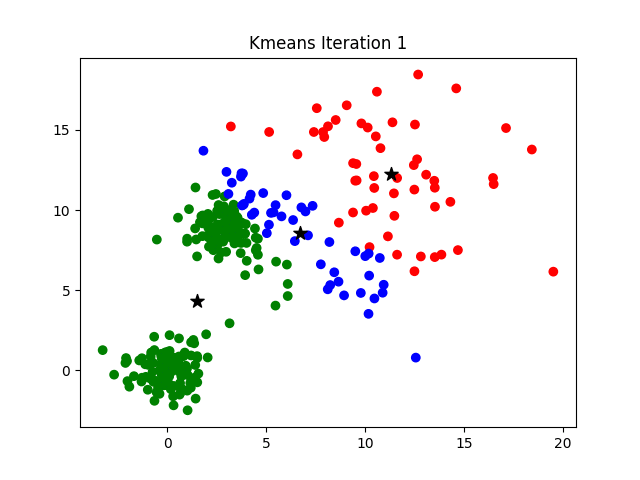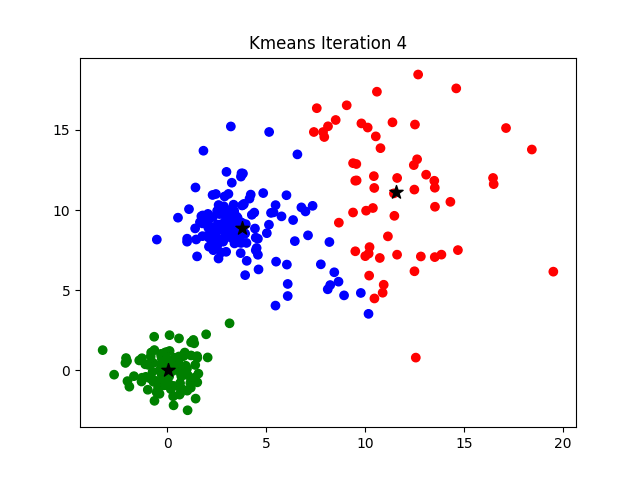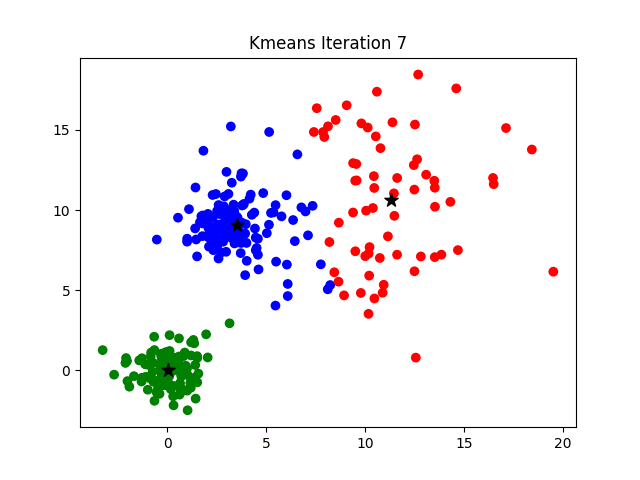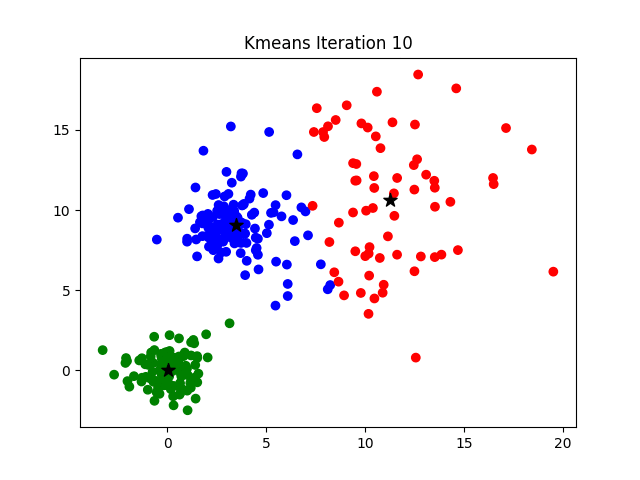
K-Means 工作流程

1. 首先, 随机确定 K 个初始点作为质心（不必是数据集中的点）。
2. 然后将数据集中的每个点分配到一个簇中, 具体来讲, 就是为每个点找到距其最近的质心, 并将其分配该质心所对应的簇.
3. 根据结果重新计算每个簇的质心.
4. 重复上述过程直到直到聚类结果不再发生变化时结束。

损失函数

假设簇划分为$(C_1,C_2,...C_k)$，则我们的目标是最小化所有簇内点到质心的距离平方和SSE：

$$SSE=\sum _{i=1}^k\sum _{x\in C_i}||x-{\mu }_i|{|}_2^2$$
其中

• ${\mu }_i=\frac{1}{|C_i|}\sum _{x\in C_i}x$是簇$C_i$的均值向量，也就是质心
• $||x-{\mu }_i|{|}_2^2$代表样本点到均值点的距离,这里其实就是欧式距离的平方，用范数的方式表示。

聚类个数K的问题

由于 K-means算法需要人为指定最终的簇（类别）的个数K,且K 值的选取对结果影响很大，如果错误地指定了簇的数量，则聚类结果的效果就会变得很差

所以在事先不知道分成多少簇的情况下我们需要通过一些方法来确定最终的K值。常见的选取 K 值的方法有：
肘部法（The elbow method），轮廓系数法 ，间隔量统计（The gap statistic）

聚类结果效果的评价标准

首先如何定量评估聚类结果是好还是坏？ 想象以下场景，相同的数据集分为三个簇。 左侧的聚类定义良好，而右侧的聚类识别不佳。

聚类的目标是对聚类中的数据点进行分组，要求：
(1) 聚类内的点尽可能相似
(2) 属于不同聚类的点尽可能不同。
这意味着，在理想的聚类中，簇内间距小，而簇间间距大。因此，一个好的聚类质量度量应该能够定量地总结以上两点

肘部法

假设最佳的分类数目为$k$，考虑前面损失函数中给出的所有簇内点到质心的距离平方和。由于要求簇内间距小，而簇间间距大，所以当设定的簇数量小于$k$时，距离和会包括簇间间距，导致距离平方和较大。同时增加分类数量会减少参与计算的簇间间距，使距离和快速减小，而大于$k$时速度下降很慢，因为这时计算的平方和与最佳分类$k$时相比都是计算簇内间距。所以总体上减小趋势会出现先快后慢的特点。

所以可以计算一定范围内的$k$对应的距离平方和，找到由快到慢的点就是最佳的分类个数。一般选取分类数目的最大值为$\sqrt{n}$

但是肘部法依赖于人工判断，例如上图中有些人可能会选择$k=4$作为最优分类数，有些人则会选择$k=6$作为最优分类数.

轮廓系数法

轮廓系数可以提供更客观的方法来确定最佳聚类数。

一个样本的轮廓系数的定义为：
$$S_i=\frac{b_i-a_i}{max(a_i,b_i)}$$
其中$a_i$是样本i与其所在簇内其他样本的平均距离（即簇内间距）,$b_i$是样本i到与其他簇样本的平均距离（即簇间间距），值得范围在[-1,1]之间.

总体的轮廓系数SC为：
$$SC=\frac{1}{N}\sum _{i=1}^N{S}_i$$
即将所有样本的轮廓系数均值作为聚类结果的轮廓系数，用于衡量聚类效果的好坏。之前说过理想的聚类中，簇内间距小，而簇间间距大，所以轮廓系数越接近1则聚类效果越好。但是由于簇内间距$a_i$一般不为0，所以轮廓系数最终一般也取不到1.

调整兰德系数

首先介绍一下兰德系数(Rand index, RI)

假设U是外部评价标准，即true_label， 而V是聚类结果，设定4个统计量
TP ：在U中为同一类，且在V中也为同一类别的数据点对数，即将相似的样本归为同一个簇(同–同)，正确的决策
TN ：在U中不在同一类，且在V中也不属于同一类别的数据点对数，将不相似的样本归入不同的簇(不同–不同)，正确的决策
FP ：在U中不在同一类，但在V中维同一类的数据点对数，将不相似的样本归为同一个簇(不同–同)，错误的决策
FN ：在U中为同一类，但在V中却隶属于不同类别的数据点对数，将相似的样本归入不同的簇(同–不同)，错误的决策

则RI的计算公式为：
$$RI=\frac{TP+TN}{TP+FP+TN+FN}=\frac{TP+TN}{C_N^2}=\frac{TP+TN}{C_2^{n_{samples}}}$$

RI的范围为[0,1]，分母$C_N^2$和$C_2^{n_{samples}}$表示任意两个样本为一类有多少种组合，是数据集中可以组成的总元素对数

调整兰德指数(Adjusted Rand index, ARI)计算公式为：
$$ARI=\frac{RI-E(RI)}{max(RI)-E(RI)}$$
ARI的范围为[-1,1]。调整兰德系数也是越接近于1，则说明聚类效果越好。

Kmeans算法优化

Kmeans++算法

原始Kmeans算法最开始随机选取数据集中k个点作为聚类中心，k个初始化的质心的位置选择对最后的聚类结果和运行时间都有很大的影响，因此需要选择合适的k个质心。如果仅仅是完全随机的选择，有可能导致算法收敛很慢。例如初始的k个点全部选在了同一个簇内，那么可能会导致分类结果错误。Kmeans++算法主要对对K-Means初始值选取的方法的优化。

Kmeans++算法初始点的选择过程如下：

1. 从数据集中随机选择一个中心。
2. 接着计算每个样本与当前已有聚类中心之间的最短距离，用$D(x)$表示；然后计算每个样本点被选为下一个聚类中心的概率$P(x)$,其中$P(x)=\frac{D(x{)}^2}{\sum D(x{)}^2}$，最后选择最大概率值（或者概率分布）所对应的样本点作为下一个簇中心；。
3. 重复步骤2，直到选择了K个中心。
   其余训练过程与KMeans一致。

从计算概率距离$P(x)$的公式可以看出，离现有簇中心越远的样本点，越可能被选为下一个簇中心

二分 K-Means 聚类算法

二分K-Means算法流程为：

1. 初始化：将所有数据点视为一个簇。
2. 分裂：从当前的簇中选择一个簇进行分裂。选择的标准通常是选择那些分裂后可以最大程度减少误差平方和（SSE）的簇。
3. 应用K-Means：对选定的簇应用标准的K-Means算法，将其分成两个簇。
4. 评估：检查是否达到了所需的聚类数目。如果没有，返回步骤2；如果达到了，算法结束

二分 K-Means 聚类算法可以以更快的速度收敛。

总结

最后总结一下K-means算法的适用条件及优缺点。

适用条件

K-means算法适合使用数值型属性的数据集（可用于欧式距离计算），而非使用类别型属性。

优点

• 实现原理简洁易懂。
• 算法属于无监督学习。

缺点

• 可能存在数据点使得聚类计算无法收敛，这就需要人为指定最大迭代次数。
• 需要给定期望将数据分为几个群簇(组)的初始K值。
  K-means算法需要提前设定聚类数K，这个值的选择往往需要根据具体问题和数据特点来确定。如果K值选择不当，可能会导致聚类结果不符合实际情况或无法有效揭示数据的内在结构。在实际应用中，可以通过一些评估指标（如轮廓系数、肘部法则等）来辅助确定合适的K值。
• K-means算法对初始聚类中心敏感
  K-means算法的聚类结果在很大程度上受到初始聚类中心选择的影响。如果初始聚类中心选择不当，可能会导致聚类结果出现偏差或迭代次数较多导致计算结果不稳定。为了缓解这一问题，可以采用一些启发式方法（如K-means++算法）来优化初始聚类中心的选择。