深度学习前置知识
文章目录
- 介绍
- 数据操作
- 张量
- 张量的定义
- 1. **张量的维度(Rank)**
- 2. **张量的形状(Shape)**
- 简单的数据预处理(插值
- 线性代数
- 微积分
- 概率论
- 1. 基本概念
- (1) 随机试验与事件
- (2) 概率公理(Kolmogorov公理)
- 2. 概率公式
- (1) 条件概率
- (2) 全概率公式
- (3) 贝叶斯定理
- 3. 随机变量与分布
- (1) 随机变量类型
- (2) 常见分布
- (3) 期望与方差
- 4. 极限定理
- (1) 大数定律
- (2) 中心极限定理(CLT)
- 5. 联合分布与独立性
- (1) 联合概率
- (2) 独立性
- (3) 协方差与相关系数
课程学习自李牧老师B站的视频和网站文档
https://zh-v2.d2l.ai/chapter_preliminaries
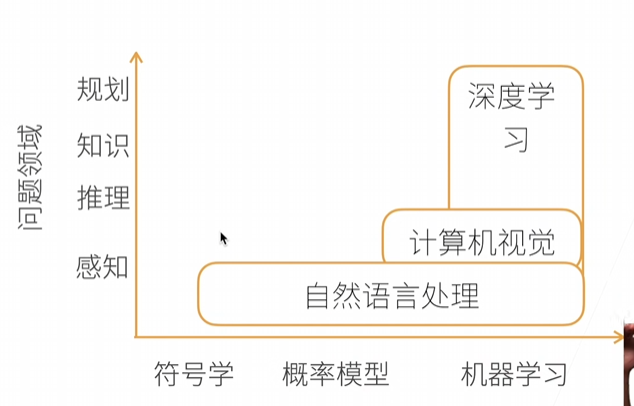
介绍
深度学习是机器学习的一种,可以做计算机视觉,可以做自然语言处理
- 在图片分类出现了较大的突破
- 可以物体检测和分割
- 可以样式迁移(类似换背景
- 可以人脸合成(随机生成的
- 可以文字生成图片
- 文字生成模型(AI大模型
数据操作
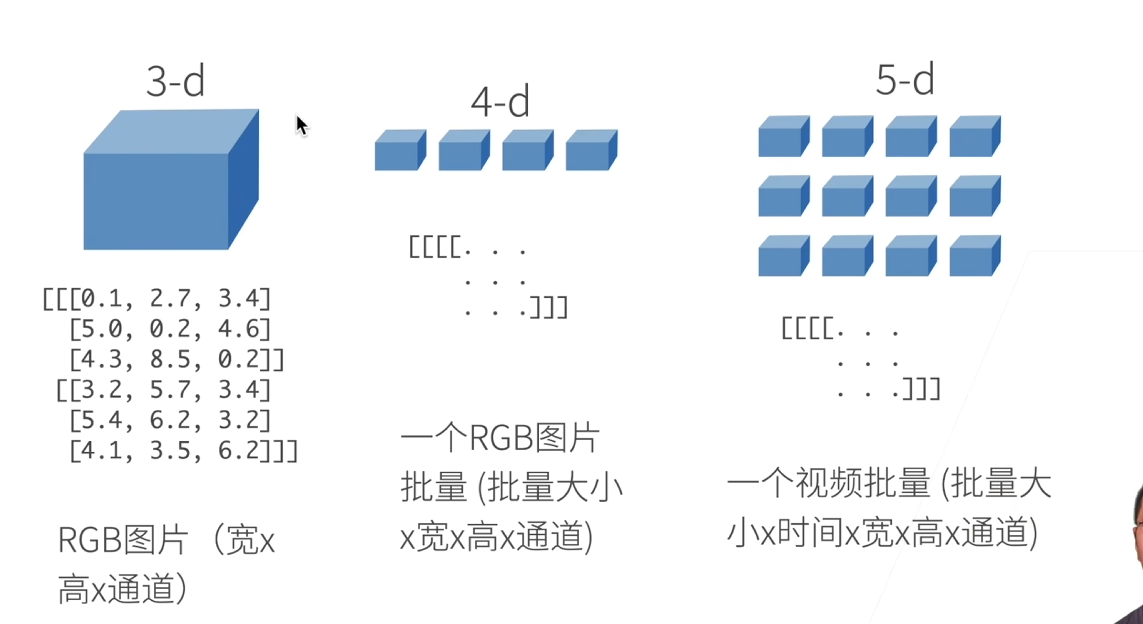
N维数组时机器学习和神经网络的主要数据结构
- 0-d:标量(1.0这样的一个类别
- 1-d:向量(【1.0,2.7,3.4】这样的一个特征向量
- 2-d:矩阵(一个样本,也就是特征矩阵
访问元素:
- 【1:】把第一行拿出来
- 【::3】每三行一跳
张量
张量的定义
- 标量:0维张量,例如一个数字(如 5)。
- 向量:1维张量,例如 [1, 2, 3]。
- 矩阵:2维张量,例如 [[1, 2], [3, 4]]。
- 高维张量:3维或更高,例如表示图像的张量(宽×高×通道)。
1. 张量的维度(Rank)
- 维度指的是张量的轴(axes)数量,表示张量是几维的。
- 例如:
- 0维:标量(如 5),无轴。
- 1维:向量(如 [1, 2, 3]),1个轴。
- 2维:矩阵(如 [[1, 2], [3, 4]]),2个轴。
- 3维及以上:高维张量(如 [[[1, 2], [3, 4]], [[5, 6], [7, 8]]]),3个轴或更多。
- 维度也叫阶(rank),例如2维张量的阶是2。
2. 张量的形状(Shape)
-
形状是一个元组,描述张量在每个轴上的元素数量。
-
例如:
- 标量:形状是 ()(空元组)。
- 向量 [1, 2, 3]:形状是 (3,),表示1个轴有3个元素。
- 矩阵 [[1, 2], [3, 4]]:形状是 (2, 2),表示2行2列。
- 3维张量 [[[1, 2], [3, 4]], [[5, 6], [7, 8]]]:形状是 (2, 2, 2),表示2个矩阵,每个矩阵2行2列。
import torch# 标量(0维) scalar = torch.tensor(5) print(scalar.shape) # 输出:torch.Size([])# 向量(1维) vector = torch.tensor([1, 2, 3]) print(vector.shape) # 输出:torch.Size([3])# 矩阵(2维) matrix = torch.tensor([[1, 2], [3, 4]]) print(matrix.shape) # 输出:torch.Size([2, 2])# 3维张量 tensor_3d = torch.tensor([[[1, 2], [3, 4]], [[5, 6], [7, 8]]]) print(tensor_3d.shape) # 输出:torch.Size([2, 2, 2])x.reshape函数只改变张量的形状
tensor.zeros创建全0的张量
cat函数将张量连结在一起

x.sum()函数求和
两个张量维度一样,但形状不一样,可以通过广播机制执行(每个张量自动复制自己比另一个张量低的形状
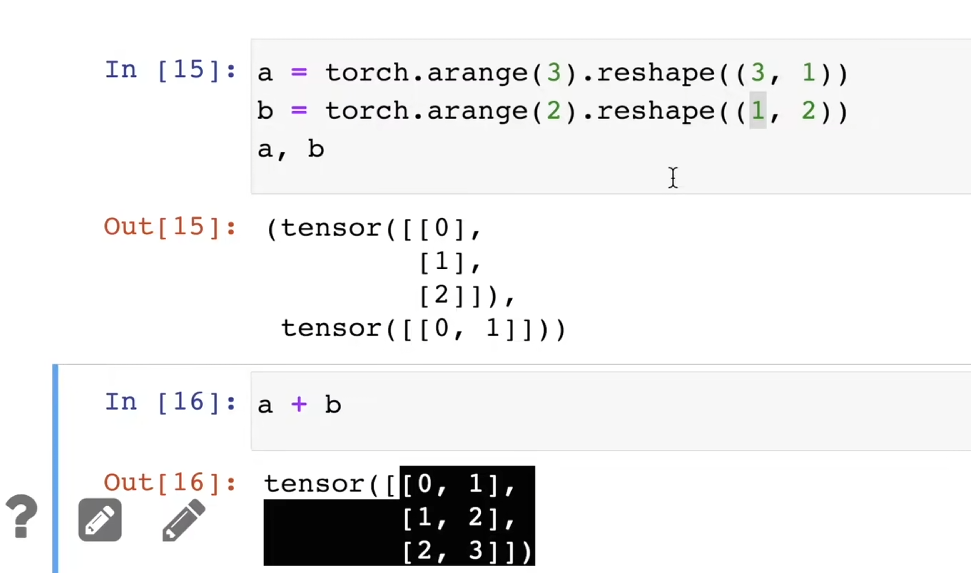
python用id标识元素地址,类似指针,在pytorch中有一些原地操作的函数
原地操作直接修改张量的值,而不是返回一个新张量。
在 PyTorch 中,原地操作通常以方法名后加下划线 _ 标记,例如 .add_()、.mul_()。
转换为numpy张量
A = X.numpy()
B = torch.tensor(A)
type(A), type(B)
(numpy.ndarray, torch.Tensor)
简单的数据预处理(插值
假设我们有这样的一个csv文件
import pandas as pddata = pd.read_csv(data_file)
print(data)NumRooms Alley Price
0 NaN Pave 127500
1 2.0 NaN 106000
2 4.0 NaN 178100
3 NaN NaN 140000
这里我们使用插值的方式处理,假设price可能缺失,我们就把它单独分出来作为output,其他作为input
input中如果是数值类,则将NaN替换为其他数的平均值
inputs, outputs = data.iloc[:, 0:2], data.iloc[:, 2]
inputs = inputs.fillna(inputs.mean())
print(inputs)NumRooms Alley
0 3.0 Pave
1 2.0 NaN
2 4.0 NaN
3 3.0 NaN
如果是字符类,我们采用数字01来代替存在
inputs = pd.get_dummies(inputs, dummy_na=True)
print(inputs)NumRooms Alley_Pave Alley_nan
0 3.0 1 0
1 2.0 0 1
2 4.0 0 1
3 3.0 0 1
线性代数
一些基本的概念



对某一维求和,其实就是沿着选择的方向做一个压缩
保持维度:用 keepdim=True 保留求和后的维度,便于后续操作


微积分
在深度学习中,我们“训练”模型,不断更新它们,使它们在看到越来越多的数据时变得越来越好。 通常情况下,变得更好意味着最小化一个损失函数(loss function), 即一个衡量“模型有多糟糕”这个问题的分数。 最终,我们真正关心的是生成一个模型,它能够在从未见过的数据上表现良好。 但“训练”模型只能将模型与我们实际能看到的数据相拟合。 因此,我们可以将拟合模型的任务分解为两个关键问题:
- 优化(optimization):用模型拟合观测数据的过程;
- 泛化(generalization):数学原理和实践者的智慧,能够指导我们生成出有效性超出用于训练的数据集本身的模型。

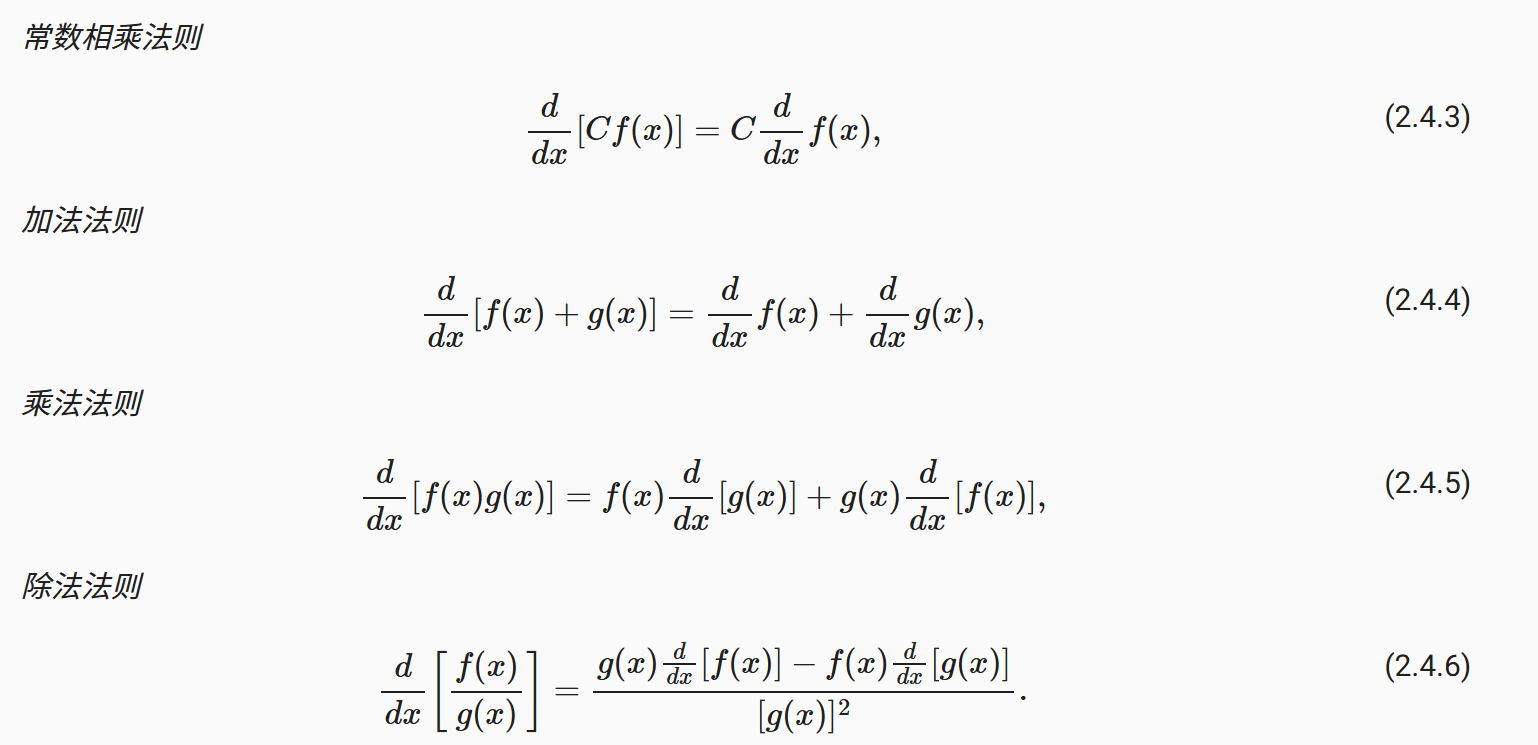
偏导数:假如y有多个变量x1,x2,x3等,对其中一个变量求导,其余变量视为常数
梯度:对每个变量求偏导数,结果合成一个向量


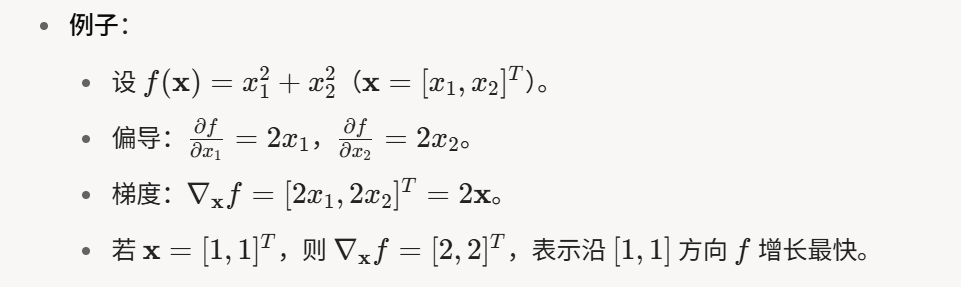
fx是一个输入x1和x2这两个向量得到一个标量(固定结果,可能数数字)的标量函数,而x可能是向量,求标量函数关于向量的梯度,其实就是说求fx这函数的每个x的偏导数
链式法则求导


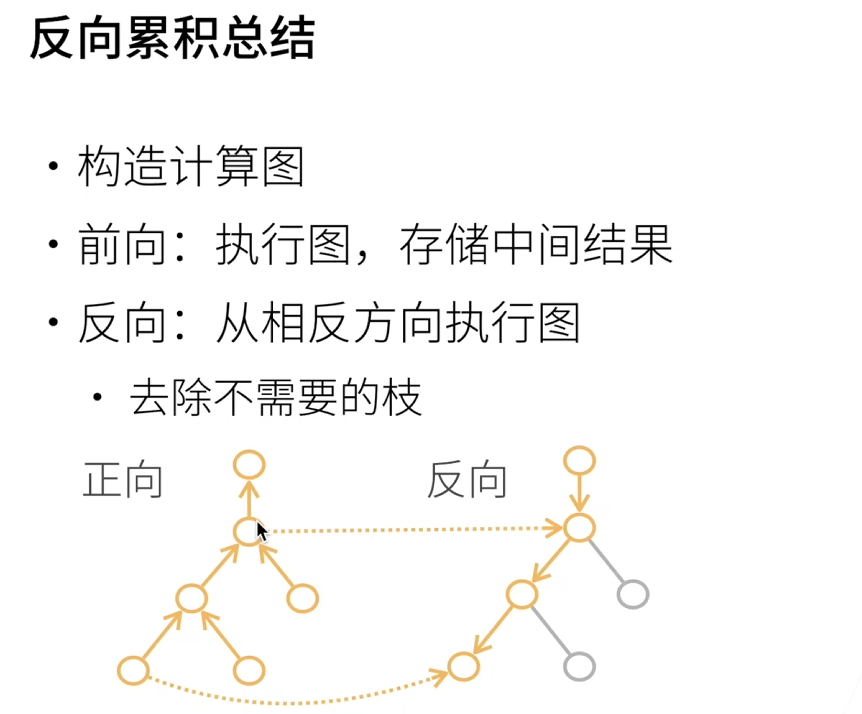
反向需要把正向存储的中间结果拿过来用
非标量反向传播依赖自动微分工具(如 PyTorch 的 .backward()),手动推导需注意维度匹配。
梯度累积可能需要清零(如 optimizer.zero_grad())。
计算图的概念:

分离计算:假如我们希望将y视为一个常数,可以引入变量u
x.grad.zero_()
y = x * x
u = y.detach()
z = u * xz.sum().backward()
x.grad == u
由于记录了y的计算结果,我们可以随后在y上调用反向传播, 得到y=x*x关于的x的导数,即2*x
x.grad.zero_()
y.sum().backward()
x.grad == 2 * x
使用自动微分的一个好处是: 即使构建函数的计算图需要通过Python控制流(例如,条件、循环或任意函数调用),我们仍然可以计算得到的变量的梯度。 在下面的代码中,while循环的迭代次数和if语句的结果都取决于输入a的值。
def f(a):b = a * 2while b.norm() < 1000:b = b * 2if b.sum() > 0:c = belse:c = 100 * breturn c
a = torch.randn(size=(), requires_grad=True)
d = f(a)
d.backward()
概率论
1. 基本概念
(1) 随机试验与事件
- 样本空间:Ω={所有可能结果}\Omega = \{\text{所有可能结果}\}Ω={所有可能结果}
例:掷骰子的样本空间 Ω={1,2,3,4,5,6}\Omega = \{1, 2, 3, 4, 5, 6\}Ω={1,2,3,4,5,6}。 - 事件:A⊆ΩA \subseteq \OmegaA⊆Ω,如“掷出偶数”对应 A={2,4,6}A = \{2, 4, 6\}A={2,4,6}。
(2) 概率公理(Kolmogorov公理)
对任意事件 AAA:
- 非负性:P(A)≥0P(A) \geq 0P(A)≥0
- 规范性:P(Ω)=1P(\Omega) = 1P(Ω)=1
- 可列可加性:若 A1,A2,…A_1, A_2, \dotsA1,A2,… 互斥,则 P(⋃iAi)=∑iP(Ai)P\left(\bigcup_{i} A_i\right) = \sum_i P(A_i)P(⋃iAi)=∑iP(Ai)。
2. 概率公式
(1) 条件概率
P(A∣B)=P(A∩B)P(B)(P(B)>0)P(A \mid B) = \frac{P(A \cap B)}{P(B)} \quad (P(B) > 0) P(A∣B)=P(B)P(A∩B)(P(B)>0)
(2) 全概率公式
若 B1,B2,…,BnB_1, B_2, \dots, B_nB1,B2,…,Bn 是 Ω\OmegaΩ 的划分:
P(A)=∑i=1nP(A∣Bi)P(Bi)P(A) = \sum_{i=1}^n P(A \mid B_i) P(B_i) P(A)=i=1∑nP(A∣Bi)P(Bi)
(3) 贝叶斯定理
P(Bi∣A)=P(A∣Bi)P(Bi)∑jP(A∣Bj)P(Bj)P(B_i \mid A) = \frac{P(A \mid B_i) P(B_i)}{\sum_j P(A \mid B_j) P(B_j)} P(Bi∣A)=∑jP(A∣Bj)P(Bj)P(A∣Bi)P(Bi)
3. 随机变量与分布
(1) 随机变量类型
- 离散型:X∈{x1,x2,…}X \in \{x_1, x_2, \dots\}X∈{x1,x2,…}
- 连续型:X∈RX \in \mathbb{R}X∈R,概率密度函数 f(x)f(x)f(x) 满足 P(a≤X≤b)=∫abf(x)dxP(a \leq X \leq b) = \int_a^b f(x) dxP(a≤X≤b)=∫abf(x)dx。
(2) 常见分布
| 分布名称 | 概率质量/密度函数 | 参数 |
|---|---|---|
| 伯努利分布 | P(X=k)=pk(1−p)1−kP(X=k) = p^k (1-p)^{1-k}P(X=k)=pk(1−p)1−k | k∈{0,1}k \in \{0,1\}k∈{0,1} |
| 二项分布 | P(X=k)=(nk)pk(1−p)n−kP(X=k) = \binom{n}{k} p^k (1-p)^{n-k}P(X=k)=(kn)pk(1−p)n−k | k≤nk \leq nk≤n |
| 泊松分布 | P(X=k)=λke−λk!P(X=k) = \frac{\lambda^k e^{-\lambda}}{k!}P(X=k)=k!λke−λ | λ>0\lambda > 0λ>0 |
| 正态分布 | f(x)=1σ2πe−(x−μ)22σ2f(x) = \frac{1}{\sigma\sqrt{2\pi}} e^{-\frac{(x-\mu)^2}{2\sigma^2}}f(x)=σ2π1e−2σ2(x−μ)2 | μ,σ\mu, \sigmaμ,σ |
(3) 期望与方差
- 期望:E[X]=∑xP(x)\mathbb{E}[X] = \sum x P(x)E[X]=∑xP(x) 或 ∫xf(x)dx\int x f(x) dx∫xf(x)dx
- 方差:Var(X)=E[(X−E[X])2]\text{Var}(X) = \mathbb{E}[(X - \mathbb{E}[X])^2]Var(X)=E[(X−E[X])2]
4. 极限定理
(1) 大数定律
1n∑i=1nXi→PE[X]当 n→∞\frac{1}{n} \sum_{i=1}^n X_i \overset{P}{\to} \mathbb{E}[X] \quad \text{当} \ n \to \infty n1i=1∑nXi→PE[X]当 n→∞
(2) 中心极限定理(CLT)
∑i=1nXi−nμσn→dN(0,1)\frac{\sum_{i=1}^n X_i - n\mu}{\sigma \sqrt{n}} \overset{d}{\to} N(0, 1) σn∑i=1nXi−nμ→dN(0,1)
5. 联合分布与独立性
(1) 联合概率
- 离散型:P(X=x,Y=y)P(X=x, Y=y)P(X=x,Y=y)
- 连续型:fX,Y(x,y)f_{X,Y}(x,y)fX,Y(x,y)
(2) 独立性
XXX 与 YYY 独立 ⟺\iff⟺ P(X,Y)=P(X)P(Y)P(X,Y) = P(X)P(Y)P(X,Y)=P(X)P(Y) 或 fX,Y(x,y)=fX(x)fY(y)f_{X,Y}(x,y) = f_X(x) f_Y(y)fX,Y(x,y)=fX(x)fY(y)。
(3) 协方差与相关系数
- 协方差:Cov(X,Y)=E[(X−E[X])(Y−E[Y])]\text{Cov}(X,Y) = \mathbb{E}[(X-\mathbb{E}[X])(Y-\mathbb{E}[Y])]Cov(X,Y)=E[(X−E[X])(Y−E[Y])]
- 相关系数:ρX,Y=Cov(X,Y)σXσY∈[−1,1]\rho_{X,Y} = \frac{\text{Cov}(X,Y)}{\sigma_X \sigma_Y} \in [-1, 1]ρX,Y=σXσYCov(X,Y)∈[−1,1]
