当前位置：首页 > ds >正文

多边形生成立面点云

ds 2025/5/8 10:15:31

1、背景介绍

在进行机载点云三维重建时，墙面点云缺失，可采用根据外轮廓线生成立面，根据立面与屋顶面相交，进行三维重建，即可生成三维模型。如下图，屋顶点云完整，但立面点缺失。


屋顶点云分割	三维模型

2、ply格式介绍

polyfit算法默认点云格式为ply，ply格式大体如下：

文件头+数据内容，文件头从 ply 一行开始，到 end_header 为止，里面定义了此 ply文件中数据的组织形式，包括数据类型和个数。

如下为polyfit中ply格式，分别为坐标（x y z），点颜色（r g b），后续为点的标号segment_index，属于同一面的点标号相同，标号从1开始，第二个面标号为3，以此类推。

格式为ascii 1.0版本；

顶点数：4056，总共包含的点数为4056，每个点包含点坐标、点的颜色rgb、面片编号。

cloudcompare软件可以打开ply点云格式，在加载点云时，需要设置字段，如r g b 等，加载进来可以查看点的相关属性。

3、生成原理与步骤

生成点集大体是对每一线段，根据等距离生成点集，具体步骤如下：

（1）定义多边形顶点：

建筑物外轮廓线实际是有多个有序顶点构成，因此需要事先定义多边形顶点，顶点z坐标相同。

（2）任意顶点间距离

通过计算两点之间的距离，并根据指定的间距在直线上均匀地生成点，即等距离生成点集。点之间间距可根据实际点间距来设置，如机载点云间距，可设置成0.3m。

（3）多边形内部点生成

通过遍历多边形内部的网格点，使用射线法判断点是否在多边形内部，从而生成顶部和底部的内部点集。

（4）点集保存。

4、代码测试

4.1 点集生成测试

只保留了点的x y z r g b idx_segments。假设要生成的立面点集的多边形如下图所示，各点坐标分别为（0,0）、（1,0）、（1,2）、（3,3）、（3,5）、（-2,5）、（-2,3）、（0,2）。

基于PCL的完整代码如下：

#include <iostream>
#include <vector>
#include <cmath>
#include <fstream>
#include <algorithm>
#include <pcl/point_types.h>
using namespace std;// 计算两点之间的距离
double distance2pts(pcl::PointXYZ p1, pcl::PointXYZ p2) {return std::sqrt(std::pow(p2.x - p1.x, 2) + std::pow(p2.y - p1.y, 2));
}// 生成直线上的点，确保间距相同
std::vector<pcl::PointXYZ> generatePointsOnLineWithEqualSpacing(pcl::PointXYZ start, pcl::PointXYZ end, double spacing) {std::vector<pcl::PointXYZ> points;double dist = distance2pts(start, end);int numPoints = static_cast<int>(dist / spacing);for (int i = 0; i <= numPoints; ++i) {double t = static_cast<double>(i) / numPoints;pcl::PointXYZ p;p.x = start.x + t * (end.x - start.x);p.y = start.y + t * (end.y - start.y);p.z = start.z + t * (end.z - start.z);points.push_back(p);}return points;
}// 生成过直线段的竖直平面点集
std::vector<pcl::PointXYZ> generateVerticalPlanePoints(pcl::PointXYZ linePoint, double z_low, double z_high, double spacing) {std::vector<pcl::PointXYZ> points;int numPoints = static_cast<int>((z_high - z_low) / spacing);for (int i = 0; i <= numPoints; ++i) {double z = z_low + static_cast<double>(i)* spacing;pcl::PointXYZ p;p.x = linePoint.x;p.y = linePoint.y;p.z = z;points.push_back(p);}return points;
}// 检查点是否在多边形内部
bool isPointInsidePolygon(pcl::PointXYZ p, std::vector<pcl::PointXYZ> vertices) {int i, j;bool inside = false;for (i = 0, j = vertices.size() - 1; i < vertices.size(); j = i++) {if ((vertices[i].y > p.y) != (vertices[j].y > p.y) &&(p.x < (vertices[j].x - vertices[i].x) * (p.y - vertices[i].y) / (vertices[j].y - vertices[i].y) + vertices[i].x)) {inside = !inside;}}return inside;
}// 生成多边形内部点集
std::vector<pcl::PointXYZ> generatePointsInsidePolygonTop(std::vector<pcl::PointXYZ> vertices, double spacing, double top_z) {std::vector<pcl::PointXYZ> pointsInside;double minX = vertices[0].x, maxX = vertices[0].x, minY = vertices[0].y, maxY = vertices[0].y;for (const auto& p : vertices) {if (p.x < minX) minX = p.x;if (p.x > maxX) maxX = p.x;if (p.y < minY) minY = p.y;if (p.y > maxY) maxY = p.y;}for (double y = minY; y <= maxY; y += spacing) {for (double x = minX; x <= maxX; x += spacing) {pcl::PointXYZ p;p.x = x;p.y = y;p.z = top_z;if (isPointInsidePolygon(p, vertices)) {pointsInside.push_back(p);}}}return pointsInside;
}// 生成底部多边形
std::vector<pcl::PointXYZ> generatePointsInsidePolygonBottom(std::vector<pcl::PointXYZ> vertices, double spacing, double bottom_z) {std::vector<pcl::PointXYZ> pointsInside;double minX = vertices[0].x, maxX = vertices[0].x, minY = vertices[0].y, maxY = vertices[0].y;for (const auto& p : vertices) {if (p.x < minX) minX = p.x;if (p.x > maxX) maxX = p.x;if (p.y < minY) minY = p.y;if (p.y > maxY) maxY = p.y;}for (double y = minY; y <= maxY; y += spacing) {for (double x = minX; x <= maxX; x += spacing) {pcl::PointXYZ p;p.x = x;p.y = y;p.z = bottom_z;if (isPointInsidePolygon(p, vertices)) {pointsInside.push_back(p);}}}return pointsInside;
}// 保存生成ply格式的带颜色、面片属性的点集
int main()
{// 多边形的顶点std::vector<pcl::PointXYZ> vertices = {pcl::PointXYZ(0, 0, -1), pcl::PointXYZ(1, 0, -1), pcl::PointXYZ(1, 2, -1), pcl::PointXYZ(3, 3, -1),pcl::PointXYZ(3, 5, -1), pcl::PointXYZ(-2, 5, -1), pcl::PointXYZ(-2, 3, -1), pcl::PointXYZ(0, 2, -1)};double lineSpacing = 0.1; // 线上点的间距double z_lowest = -1; // 竖直平面的高度double z_high = -0.5; // 竖直平面的高度double verticalSpacing = 0.1; // 竖直平面上点的间距std::ofstream outFile("D:\\points.ply");outFile << "ply" << endl;outFile << "format ascii 1.0" << endl;outFile << "element vertex 4056" << endl;outFile << "property float x" << endl;outFile << "property float y" << endl;outFile << "property float z" << endl;outFile << "property int r" << endl;outFile << "property int g" << endl;outFile << "property int b" << endl;outFile << "property int segment_index" << endl;//面片的编号从1开始计数outFile << "end_header" << endl;//面片的编号从1开始计数// 生成多边形立面的点集int idx_segments = 1;for (size_t i = 0; i < vertices.size(); ++i){int r = rand() % 255;int g = rand() % 255;int b = rand() % 255;pcl::PointXYZ start = vertices[i];pcl::PointXYZ end = vertices[(i + 1) % vertices.size()]; // 循环回到第一个点std::vector<pcl::PointXYZ> linePoints = generatePointsOnLineWithEqualSpacing(start, end, lineSpacing);vector<pcl::PointXYZ> planeallpts;//计算面的方程//(1)先统计所有点for (pcl::PointXYZ p : linePoints){planeallpts.push_back(p);std::vector<pcl::PointXYZ> verticalPoints = generateVerticalPlanePoints(p, z_lowest, z_high, verticalSpacing);for (pcl::PointXYZ vp : verticalPoints){planeallpts.push_back(vp);}}for (pcl::PointXYZ p : linePoints){outFile << p.x << " " << p.y << " " << p.z << " "   << r << " " << g << " " << b << " " << idx_segments << endl;std::vector<pcl::PointXYZ> verticalPoints = generateVerticalPlanePoints(p, z_lowest, z_high, verticalSpacing);for (pcl::PointXYZ vp : verticalPoints){outFile << vp.x << " " << vp.y << " " << vp.z << " " << r << " " << g << " " << b << " " << idx_segments << endl;}}idx_segments = idx_segments + 1;}// 生成多边形内部的点集    顶部std::vector<pcl::PointXYZ> pointsInside = generatePointsInsidePolygonTop(vertices, lineSpacing, z_high);int r = rand() % 255;int g = rand() % 255;int b = rand() % 255;for (const auto& p : pointsInside) {outFile << p.x << " " << p.y << " " << p.z  << " " << r << " " << g << " " << b << " " << idx_segments << endl;}idx_segments = idx_segments + 1;// 生成多边形内部的点集   底部pointsInside = generatePointsInsidePolygonBottom(vertices, lineSpacing, z_lowest);r = rand() % 255;g = rand() % 255;b = rand() % 255;for (pcl::PointXYZ p : pointsInside) {outFile << p.x << " " << p.y << " " << p.z  << " " << r << " " << g << " " << b << " " << idx_segments << endl;}outFile.close();return 0;
}

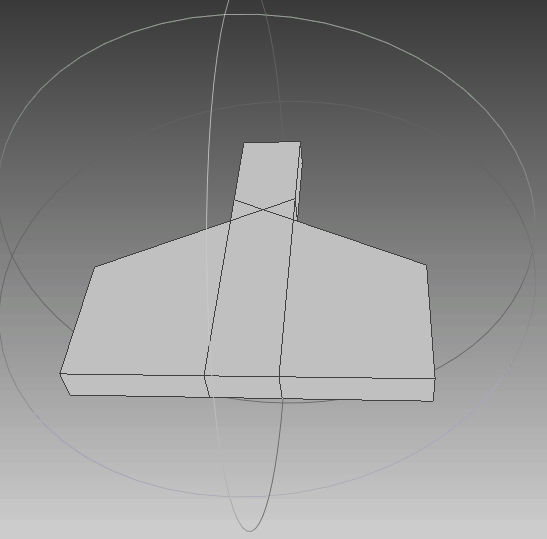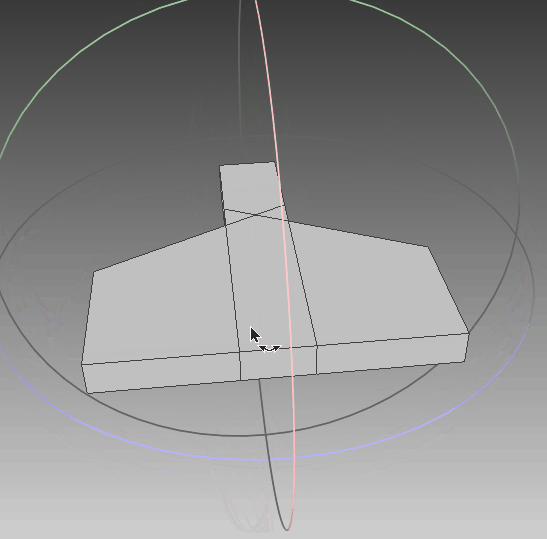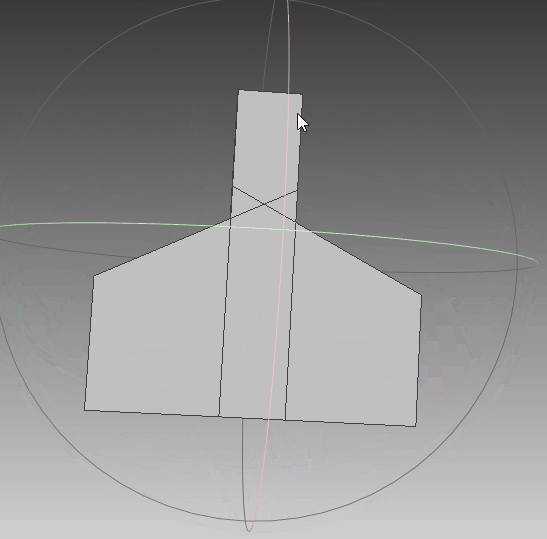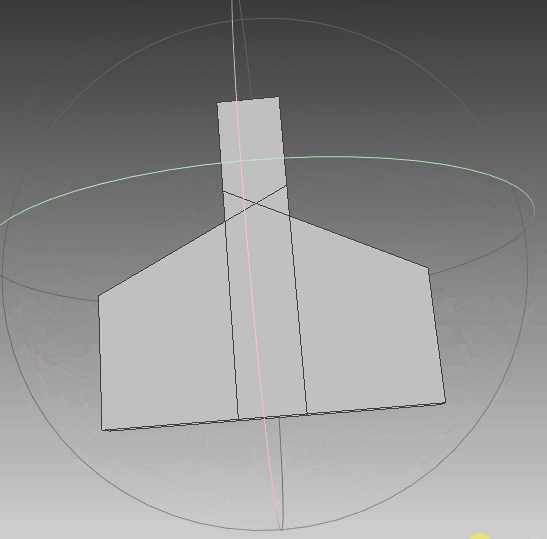
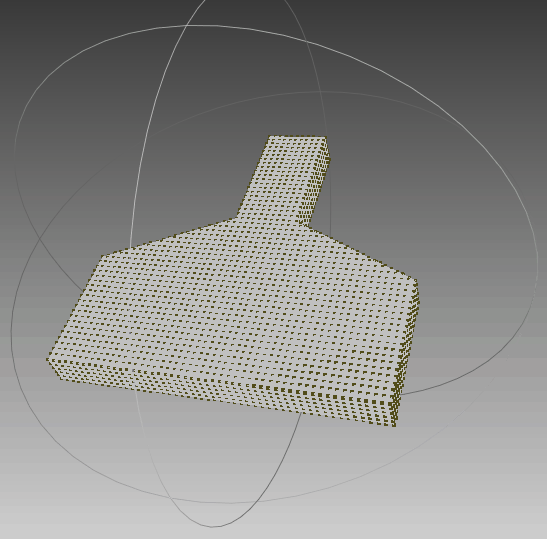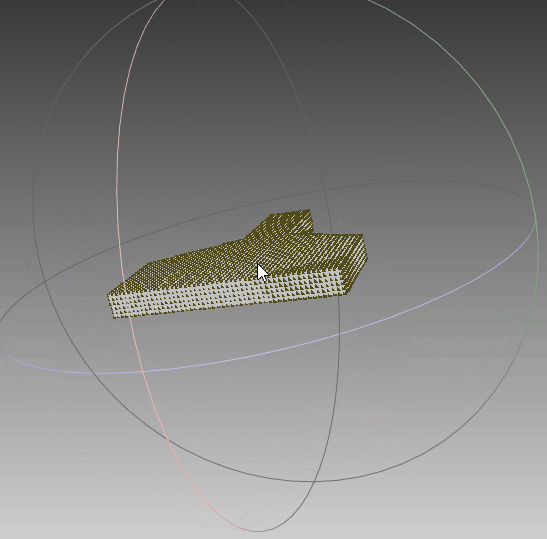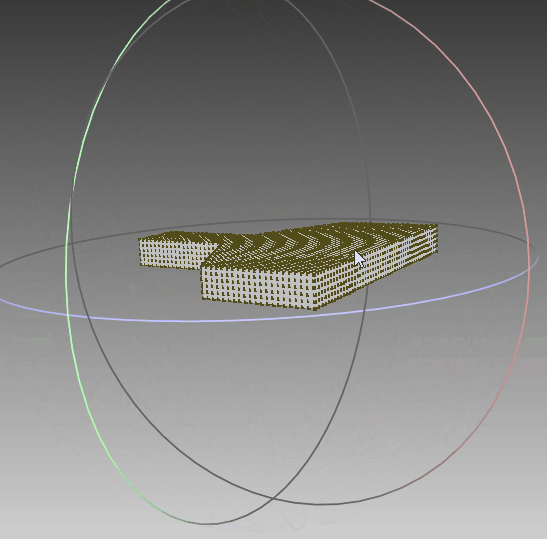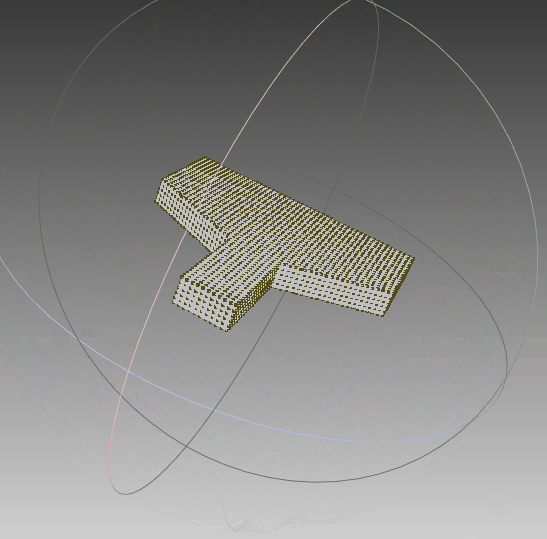
依据上述多边形，生成的点集如下图所示，可以发现生成的点集符合要求。