论文学习日志——忆阻器与神经网络——part1

一、关键词

1.忆阻器

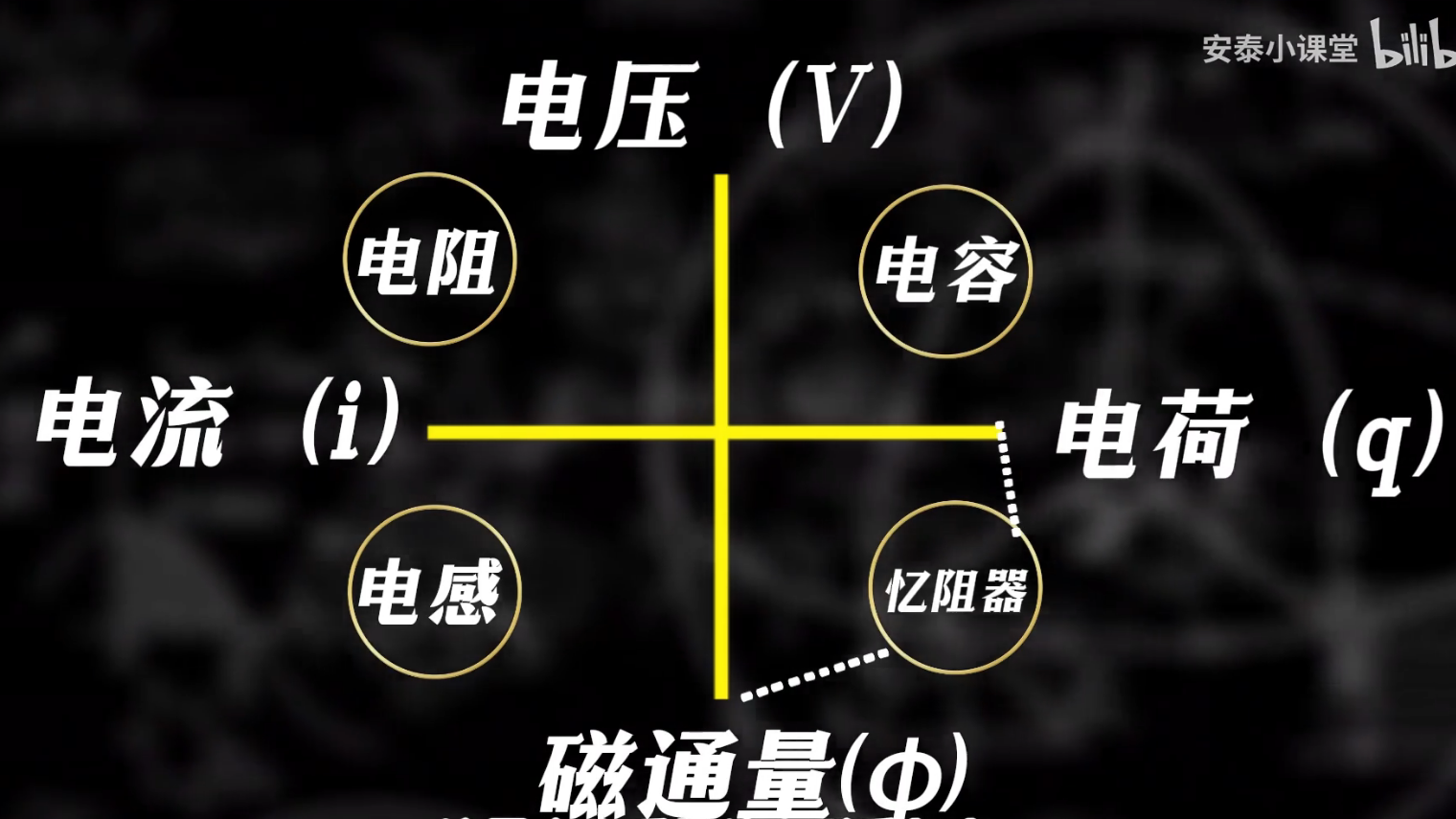
【忆阻器到底是什么？刷爆朋友圈的忆阻器究竟是个啥？】忆阻器到底是什么？刷爆朋友圈的忆阻器究竟是个啥？_哔哩哔哩_bilibili

【领跑芯片圈、高效类脑计算|忆阻器是如何发展至今的？】领跑芯片圈、高效类脑计算|忆阻器是如何发展至今的？_哔哩哔哩_bilibili

（1）特性

①电学特性

• 非易失性：电阻状态改变后能长期保持

• 电阻动态可调性：电阻值可通过外加电信号实现多阻态连续可调

• 滞回特性：

②功能特性

• 原位储存与计算:忆阻器可在存储电阻状态的同时完成计算

• 突触模拟特性：人脑的学习能力源于突触（神经元间连接）的 “可塑性”（即连接强度随信号传递历史变化），而忆阻器的电阻态随电荷历史变化的特性，可完美模拟突触可塑性

• 抗辐射与环境稳定性：部分忆阻器（如基于金属氧化物、相变材料的器件）具有抗辐射、耐高温的特性

（2）双稳态VS三稳态

（3）有源\无源\局部有源忆阻器

类型	能量依赖（核心区别）	功能范围	典型应用场景
无源忆阻器	仅依赖输入信号，无独立电源	双稳态（高 / 低阻）、低功耗记忆	高密度存储（如 RRAM 芯片）、简单逻辑门
有源忆阻器	需外部独立电源持续供电	多稳态、动态调控、信号放大	复杂神经网络（如深度学习加速器）、自适应电路
局部有源忆阻器	无需独立电源，仅在局部信号区间临时供能	多稳态、非线性振荡、低功耗调控	低功耗神经网络、混沌电路、传感器

二、函数

1.btanh（）函数

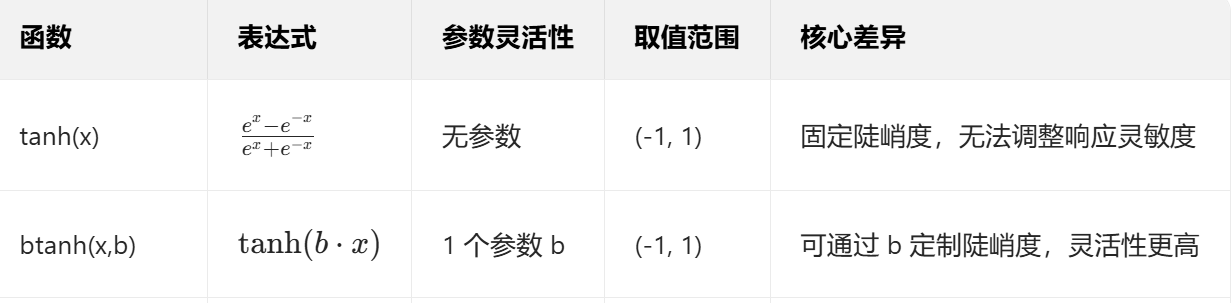
 三、专业术语解释

1.哈密顿能量

领域	形式	核心变量	物理 / 抽象意义	核心方程 / 作用
经典力学	函数 H(q,p,t)	广义坐标 q、广义动量 p	系统总机械能（动能 + 势能）	哈密顿正则方程，描述演化与能量守恒
量子力学	算符 H^	波函数 ψ	系统总能量（量子化）	薛定谔方程，求解能量本征值
神经网络	能量函数 H(s,w)	神经元状态 s、权重 w	网络状态的稳定性度量	引导网络收敛到能量极小值
非线性系统	函数 H(x,p)	状态变量 x、共轭变量 p	系统能量特性（可能非守恒）	分析相位空间演化与混沌行为

领域	形式	核心变量	物理 / 抽象意义	核心方程 / 作用
经典力学	函数 H(q,p,t)	广义坐标 q、广义动量 p	系统总机械能（动能 + 势能）	哈密顿正则方程，描述演化与能量守恒
量子力学	算符 H^	波函数 ψ	系统总能量（量子化）	薛定谔方程，求解能量本征值
神经网络	能量函数 H(s,w)	神经元状态 s、权重 w	网络状态的稳定性度量	引导网络收敛到能量极小值
非线性系统	函数 H(x,p)	状态变量 x、共轭变量 p	系统能量特性（可能非守恒）	分析相位空间演化与混沌行为

2.引力盆地

3.稳态

“稳态”（Steady State）是从器件电阻状态的稳定性角度定义的，核心是：忆阻器在没有外部激励（如电压、电流）持续作用时，能长期、稳定保持的电阻值状态。

4.相图

5.拓扑

拓扑最直观的理解是 “橡皮泥几何”—— 假设物体是可以无限拉伸、挤压、弯曲的橡皮泥（但不能撕裂、粘连或打洞 / 填洞），在这种 “连续变形” 下，物体保持不变的性质，就是 “拓扑性质”。

后续还会更新哒！！距离返校还有8天！！！