2 梯度下降算法
所学习的B站视频链接 2 梯度下降算法
文章目录
- 0 复习
- 1 模型原理
- 1.1 分治思路
- 1.2 梯度下降算法
- 1.3 梯度下降算法的数学模型推导
- 2 代码编撰
- 2.1 分块解答
- 2.2 代码综合
0 复习
上一次课堂中我们采用了最简单的线性模型进行了尝试,当时我们的输入维度和输出的维度均是一维的。
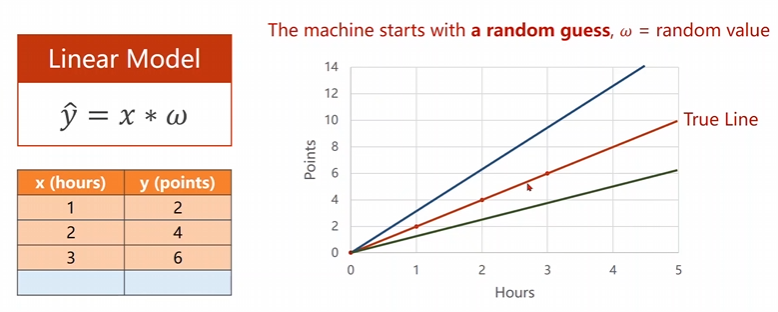
我们随机猜测我们的权重,看看什么样子的权重是可以让我们的损失函数MSEMSEMSE达到最小,采用的是一个暴力枚举法,来得到咱们的曲线。
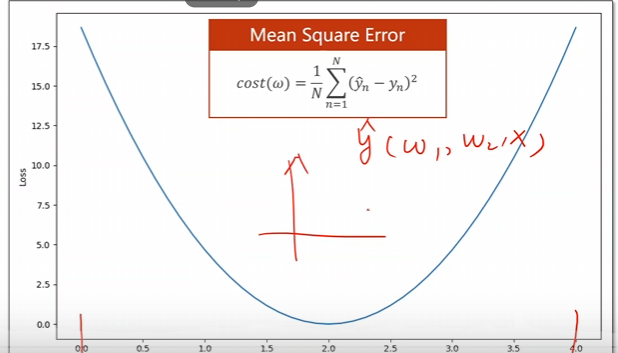
但是这仅仅只是单一权重的方法,一旦咱们的权重组合多了,这个时候咱们的程序便非常的难以运行,这个时候需要采用其他的方法和思路进行处理。
1 模型原理
1.1 分治思路
假设有W1和W2W_1和W_2W1和W2这两个权重需要寻找,在进行搜索的时候先进行一些稀疏的计算,找到可能的最小区块,然后在那个区块里面进行搜索,不断重复几轮即可。
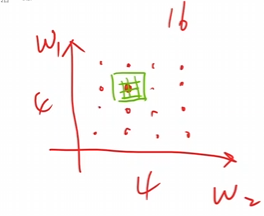
但是这个东西也不一定,因为实际上咱们的真实函数长得是非常的抽象的,而非普通的凸函数。上面的那个方法仅仅对比较好的凸函数才是可以使用的。对于下面这种函数而言,采用分治法很有可能会错过一些优秀点。

因此需要其他的方法进行使用。这种问题就是优化问题罢了。
1.2 梯度下降算法
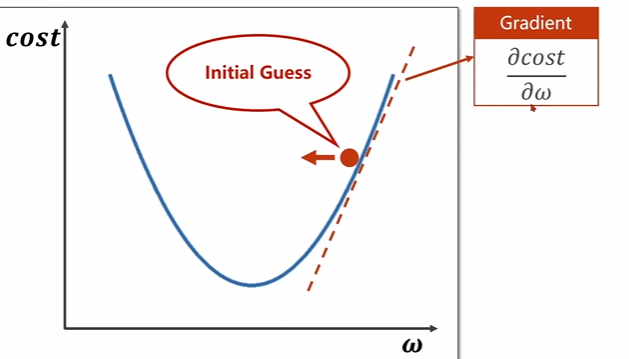
仔细看上面这个图片,咱们的红点是所需要进行下降的点,我们需要寻找使得这个点下降的方向,向左还是向右。
对函数的自变量求偏导,得到的方向是函数上升的方向,因此我们需要取导数的一个负方向进行下降,即,
w=w−α∂cost∂ww = w - \alpha\frac{\partial cost}{\partial w} w=w−α∂w∂cost
可以看出他一直向着下降速度最快的方向进行跑动-贪心,但是这个不一定能找到最优解,只能找到一定区间内的局部最优点。例如下面这个函数
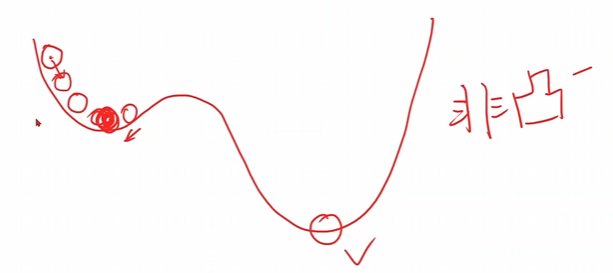
存在很多的局部最优点,这个时候采用咱们的梯度下降算法的时候是只能找到局部最优点,不能找到全局最优点。
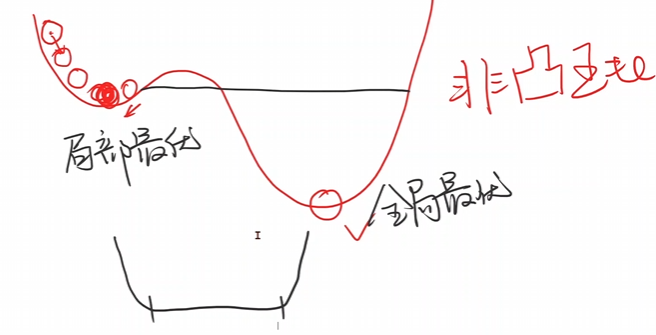
但是实际使用的过程中,咱们在进行深度学习的过程中,局部最优点是比较少的,因此大量的使用梯度下降算法。
但是会存在鞍点也就是所谓的f′=0f'=0f′=0的点
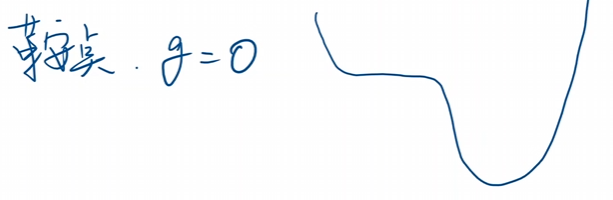
对于这个位置一旦到达时刻,便会停止迭代,此时会陷入到鞍点无法进行运动。毕竟导数为零了,学习率不论是多少都已经没有用了。
w=w−α∂cost∂w=w−0αw = w - \alpha\frac{\partial cost}{\partial w}=w - 0\alpha w=w−α∂w∂cost=w−0α
可见最大的问题就是鞍点的问题了,我们要尽可能的避免鞍点。
1.3 梯度下降算法的数学模型推导
首先先给出上一次课程的损失函数,咱们用这个函数进行推导
1N∑n=1N(xn⋅ω−yn)2\frac{1}{N}\sum_{n=1}^{N}(x_{n}\cdot\omega-y_{n})^{2} N1n=1∑N(xn⋅ω−yn)2
对这个损失函数进行求导可以得到
∂cost(ω)∂ω=∂∂ω1N∑n=1N(xn⋅ω−yn)2=1N∑n=1N∂∂ω(xn⋅ω−yn)2=1N∑n=1N2⋅(xn⋅ω−yn)∂(xn⋅ω−yn)∂ω=1N∑n=1N2⋅xn⋅(xn⋅ω−yn)\begin{aligned}\frac{\partial cost(\omega)}{\partial\omega}&=\frac{\partial}{\partial\omega}\frac{1}{N}\sum_{n=1}^{N}(x_{n}\cdot\omega-y_{n})^{2}\\&=\frac{1}{N}\sum_{n=1}^N\frac{\partial}{\partial\omega}(x_n\cdot\omega-y_n)^2\\&=\frac{1}{N}\sum_{n=1}^{N}2\cdot(x_{n}\cdot\omega-y_{n})\frac{\partial(x_{n}\cdot\omega-y_{n})}{\partial\omega}\\&=\frac{1}{N}\sum_{n=1}^{N}2\cdot x_{n}\cdot(x_{n}\cdot\omega-y_{n})\end{aligned} ∂ω∂cost(ω)=∂ω∂N1n=1∑N(xn⋅ω−yn)2=N1n=1∑N∂ω∂(xn⋅ω−yn)2=N1n=1∑N2⋅(xn⋅ω−yn)∂ω∂(xn⋅ω−yn)=N1n=1∑N2⋅xn⋅(xn⋅ω−yn)
最后可以求出来咱们的训练过程进行更新
ω=ω−α∂cost∂ω=ω−α1N∑n=1N2⋅xn⋅(xn⋅ω−yn)\begin{aligned} \omega&=\omega-\alpha\frac{\partial cost}{\partial\omega}\\ &=\omega-\alpha\frac{1}{N}\sum_{n=1}^{N}2\cdot x_{n}\cdot(x_{n}\cdot\omega-y_{n}) \end{aligned} ω=ω−α∂ω∂cost=ω−αN1n=1∑N2⋅xn⋅(xn⋅ω−yn)
这就是咱们的更新函数UpdateUpdateUpdate
2 代码编撰
2.1 分块解答
import numpy as np
import matplotlib.pyplot as plt
引入两个库函数
x_data = [1.0 , 2.0 , 3.0]
y_data = [2.0 , 4.0 , 6.0]
引入需要使用的训练集数据
global w
w = 1.0
定义一个猜测,初始化权重
def forward(x):return x*w
定义 y^\hat{y}y^ 的公式,令y^=χ∗ω\hat{y}=\chi*\omegay^=χ∗ω
def cost(xs , ys):sum = 0for x , y in zip(x_data , y_data):sum += forward(x)**2return sum/len(xs)
定义这个平均损失函数MSEMSEMSE,cost(ω)=1N∑n=1N(y^n−yn)2cost(\omega)=\frac{1}{N}\sum_{n=1}^N(\hat{y}_n-y_n)^2cost(ω)=N1∑n=1N(y^n−yn)2
def grad(xs , ys):sum = 0for x , y in zip(xs , ys):sum += 2*x*(forward(x) - y)return sum/len(xs)
定义这个梯度函数GradientGradientGradient,∂cost∂ω=1N∑n=1N2⋅xn⋅(xn⋅ω−yn)\frac{\partial cost}{\partial\omega}=\frac{1}{N}\sum_{n=1}^N2\cdot x_n\cdot(x_n\cdot\omega-y_n)∂ω∂cost=N1∑n=1N2⋅xn⋅(xn⋅ω−yn)
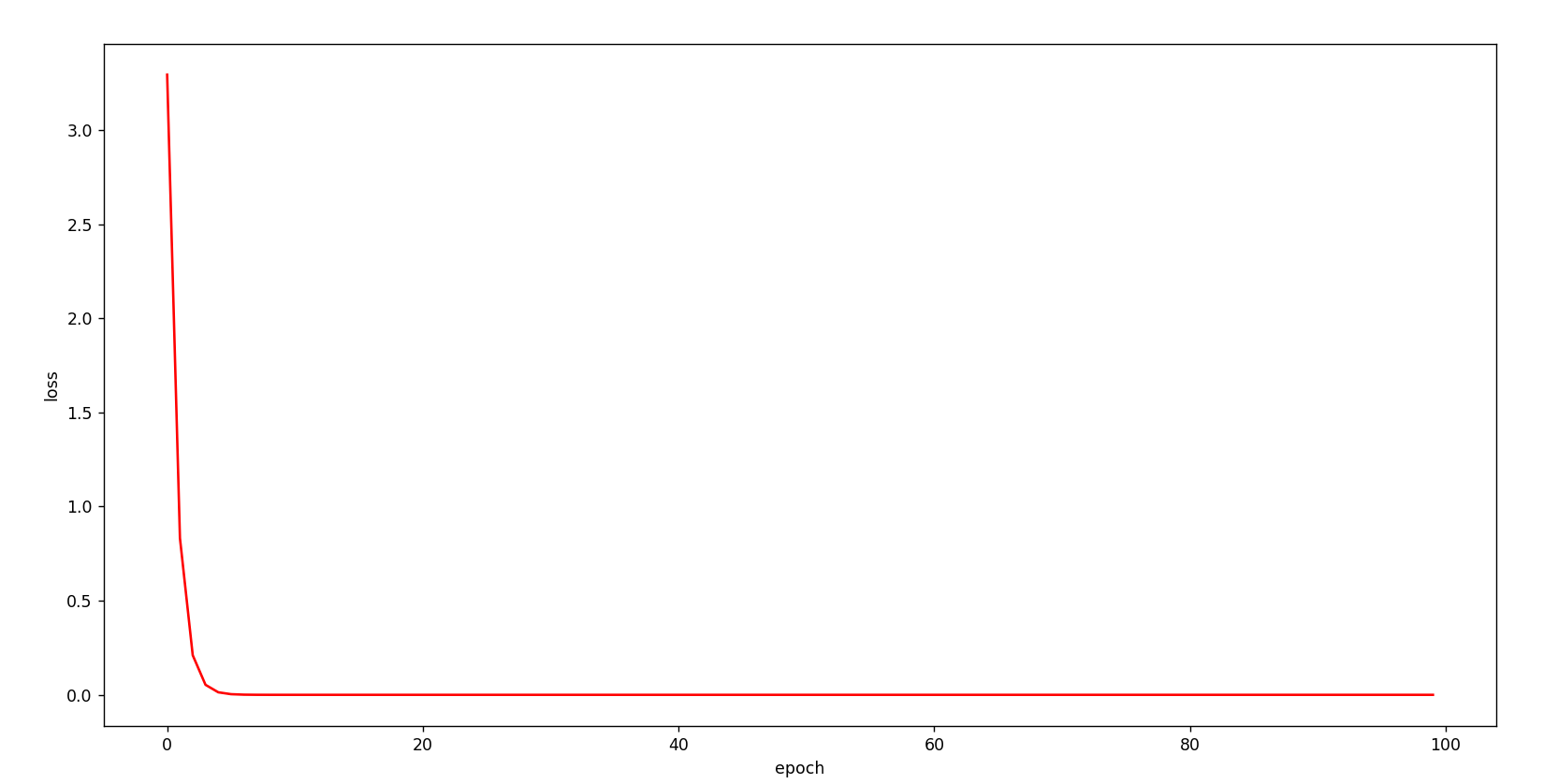
for epoch in range(100):cost_val = cost(x_data , y_data)grad_val = grad(x_data , y_data)w -= 0.01*grad_val
开始进行学习拟合处理,ω=ω−α∂cost∂ω\omega=\omega-\alpha\frac{\partial cost}{\partial\omega}ω=ω−α∂ω∂cost
训练更新的过程,这个0.0010.0010.001是学习率,这个是自己取得,凭感觉把。
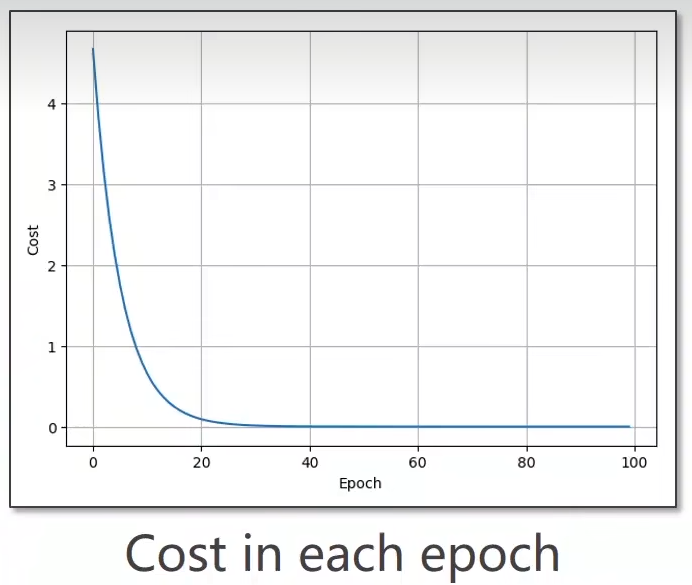
不难看出这个玩意儿是收敛到w=2w=2w=2的。
只要是总体收敛便就可以了。
当然实际上可以采用指数均值的方式将这个图像变得更加的平滑。

如果你的训练图像,学着学着,成下面这个样子,那么你就训练失败了,可以适当降低学习率。
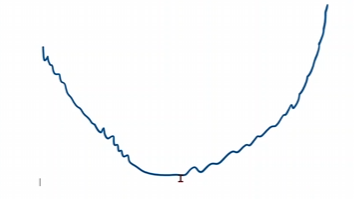
实际上我们梯度下降用的不多用的是随机梯度下降多一些。
-
更新函数
-
GradientDescent:ω=ω−α∂cost∂ωGradient Descent : \omega=\omega-\alpha\frac{\partial cost}{\partial\omega}GradientDescent:ω=ω−α∂ω∂cost
-
$ Stochastic Gradient Descent : \omega=\omega-\alpha\frac{\partial loss}{\partial\omega}$
-
-
梯度求导
-
DeribativeofCostFunction:∂cost∂ω=1N∑n=1N2⋅xn⋅(xn⋅ω−yn)Deribative of Cost Function : \frac{\partial cost}{\partial\omega}=\frac{1}{N}\sum_{n=1}^N2\cdot x_n\cdot(x_n\cdot\omega-y_n)DeribativeofCostFunction:∂ω∂cost=N1∑n=1N2⋅xn⋅(xn⋅ω−yn)
-
DerivativeofLossFunction:∂lossn∂ω=2⋅xn⋅(xn⋅ω−yn)Derivative of Loss Function : \frac{\partial loss_n}{\partial\omega}=2\cdot x_n\cdot(x_n\cdot\omega-y_n)DerivativeofLossFunction:∂ω∂lossn=2⋅xn⋅(xn⋅ω−yn)
-

从里面随机选择一个就可以了,就直接拿上单个损失直接用,注意随机二字
这个有可能可以跨过去鞍点哈,也是有点运气成分的额。
看看相对于梯度下降而言,这个随机梯度下降的代码做了些修改
def loss(x , y):y_pred = forward()return (y_pred - y)**2
重新计算损失函数,loss=(y^−y)2=(x∗ω−y)2loss=(\hat{y}-y)^{2}=(x*\omega-y)^{2}loss=(y^−y)2=(x∗ω−y)2
def grad(x , y)return 2 * x * (x*w - y)
重新计算梯度函数,∂lossn∂ω=2⋅xn⋅(xn⋅ω−yn)\frac{\partial loss_n}{\partial\omega}=2\cdot x_n\cdot(x_n\cdot\omega-y_n)∂ω∂lossn=2⋅xn⋅(xn⋅ω−yn)
for epoch in range(100):for x,y in zip(x_data , y_data):gradient = grad(x , y)w = w - 0.001 * gradientprint("\tgradient:" , x , y , gradient)l = loss(x , y)
重新进行学习更新
不过在真正的深度学习的过程中,梯度下降中每一个f(Xi)f(X_i)f(Xi)是相互独立的,是可以并行求解的。因此他的时间复杂度低,代码的效率高。但是由于计算量过大因此性能很低。

但是随机梯度下降中的www是从上一个哪来的,前后两个是由依赖的,算法的效率过低时间复杂度高,但是他的性能比较高
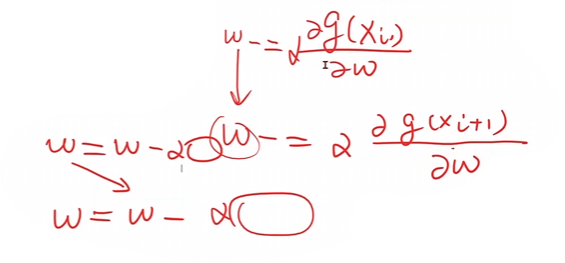
因此我们会使用Batch或是Mini−BatchBatch或是Mini-BatchBatch或是Mini−Batch进行两种算法的一个这种,一部分进行随机梯度下降,一部分进行梯度下降。分组进行使用。
2.2 代码综合
首先是最原始的梯度下降算法的代码
'''
@name: 梯度下降算法
'''import numpy as np
import matplotlib.pyplot as pltx_data = [1.0 , 2.0 , 3.0 , 4.0]
y_data = [2.0 , 4.0 , 6.0 , 8.0]w = 1.0def forward(x):# 前馈相乘求假设global wreturn x*wdef cost(xs , ys):# 计算平均误差和res = 0for x,y in zip(xs , ys):res += (x*w - y)**2res = res /len(xs)return resdef gradient(xs , ys):# 求解相应的梯度sum = 0for x , y in zip(xs , ys):sum = 2*x*(x*w-y)sum = sum/len(xs)return sum epc_list = []
cos_list = []for epoch in range(0 , 100 , 1):# 进行程序深度学习epc_list.append(epoch)cost_val = cost(x_data , y_data)cos_list.append(cost_val)grad_val = gradient(x_data , y_data)w -= alpha * grad_valplt.plot(epc_list , cos_list , 'r')
plt.xlabel('epoch')
plt.ylabel('MSE')
plt.show()
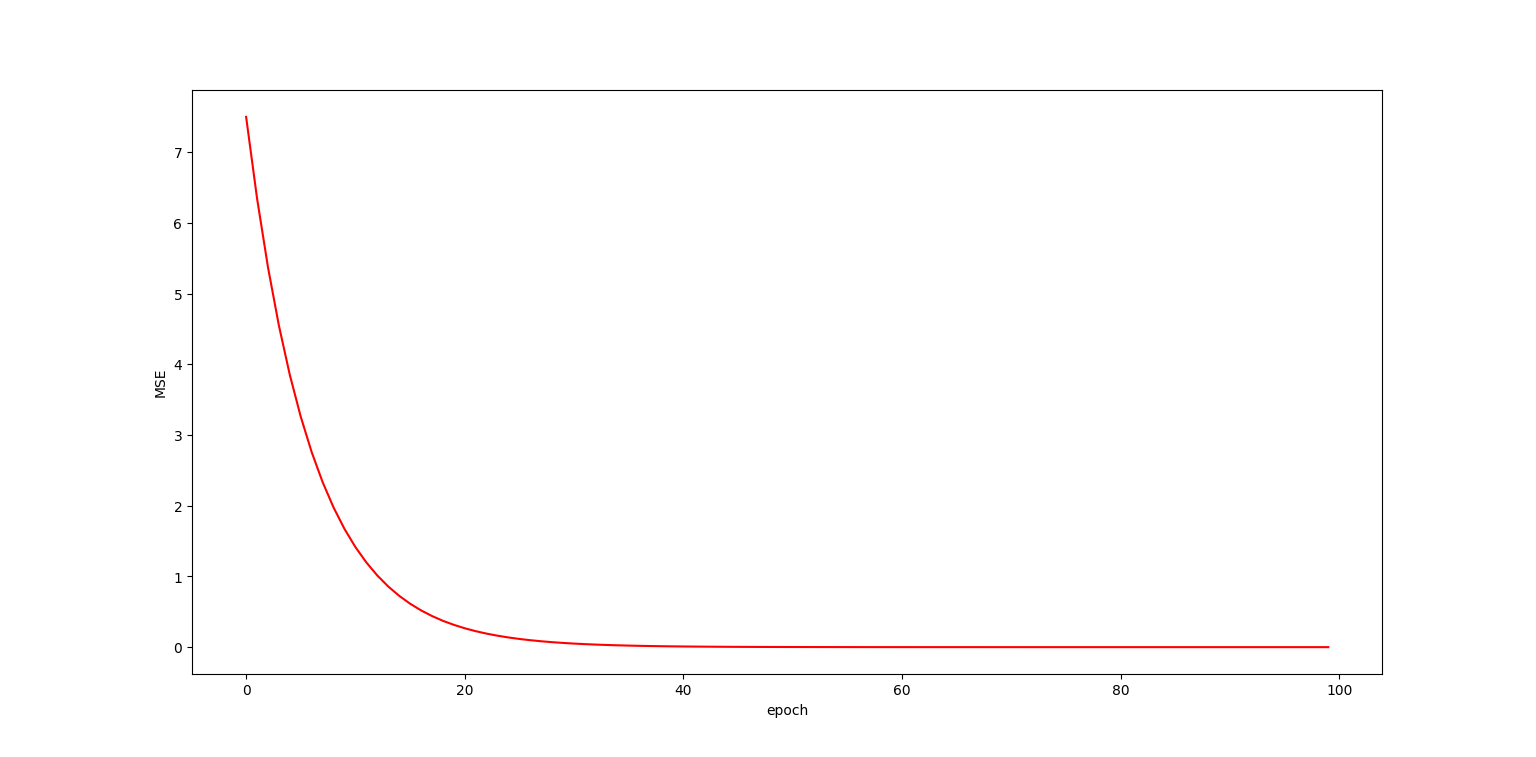
其次是更新后的随机梯度下降算法的代码
'''
@name: 随机梯度下降算法
'''import numpy as np
import matplotlib.pyplot as pltdef forward(x):# 前馈相乘求假设global wreturn x*wdef loss(x , y):# 计算平均误差和return (forward(x) - y)**2def gradient(x , y):# 求解相应的梯度return (2*x*(forward(x) - y))x_data = [1.0 , 2.0 , 3.0 , 4.0]
y_data = [2.0 , 4.0 , 6.0 , 8.0]w = 1.0
alpha = 0.01 # learning rateepc_list = []
loss_list = []
for epoch in range(0 , 100 , 1):# 进行程序深度学习epc_list.append(epoch)n = 0.0sum = 0.0for x,y in zip(x_data , y_data):n+=1grad = gradient(x , y)w = w - 0.01 * gradl = loss(x , y)sum += lsum =sum / nloss_list.append(sum)plt.plot(epc_list , loss_list , 'r')
plt.xlabel('epoch')
plt.ylabel('loss')
plt.show()