GRPO算法:告别PPO内存炸弹,无需价值函数,用组内排名代替绝对评分
GRPO算法:告别PPO内存炸弹,无需价值函数,用组内排名代替绝对评分
- 论文大纲
- 1. 按照逻辑关系中文拆解【GRPO解法】
- 技术拆解(公式形式)
- 与同类算法的主要区别
- 2. 子解法逻辑链(决策树形式)
- 3. 隐性方法分析
- 4. 隐性特征分析
- 5. 潜在局限性
- 6. 多题一解的通用解题思路
- 2. 全流程优化分析
- 多题一解特征分析
- 一题多解分析
- 更优解法探索
- 3. 医疗领域应用示例
- 输入输出定义
- 医疗GRPO全流程
论文:DeepSeekMath: Pushing the Limits of Mathematical Reasoning in Open Language Models
代码:https://github.com/deepseek-ai/DeepSeek-Math
DeepSeekMath通过三阶段方法实现数学推理突破:从Common Crawl收集120B高质量数学tokens进行预训练,用776K样本进行指令微调,创新GRPO算法进行强化学习优化。
核心机制是迭代数据收集管道和组相对策略优化(GRPO算法),最终在竞赛级MATH基准上达到51.7%准确率,逼近GPT-4性能。
GRPO通过组内奖励均值替代PPO的价值函数基线估计,使用归一化优势函数Âᵢ,ₜ=(rᵢ-mean®)/std®配合直接KL散度正则化,在零额外参数开销下将强化学习内存消耗降低80%同时保持性能。
论文大纲
├── DeepSeekMath【数学推理语言模型】
│ ├── 1. 研究背景【问题定义】
│ │ ├── 数学推理的挑战性【现状描述】
│ │ │ ├── 复杂结构化特征【技术难点】
│ │ │ └── 开源模型性能落后【性能差距】
│ │ └── 研究动机【目标设定】
│ │ ├── 逼近GPT-4性能【性能目标】
│ │ └── 推动开源发展【社区贡献】
│ │
│ ├── 2. 数学预训练【核心方法】
│ │ ├── DeepSeekMath语料库【数据构建】
│ │ │ ├── 120B数学tokens【数据规模】
│ │ │ ├── Common Crawl来源【数据源】
│ │ │ └── 迭代收集管道【收集方法】
│ │ │ ├── fastText分类器【技术工具】
│ │ │ └── 四轮迭代优化【优化过程】
│ │ └── DeepSeekMath-Base 7B【基础模型】
│ │ ├── DeepSeek-Coder初始化【起点选择】
│ │ ├── 500B tokens训练【训练规模】
│ │ └── 代码训练的益处【关键发现】
│ │ ├── 提升工具使用能力【能力增强】
│ │ └── 改善推理能力【能力增强】
│ │
│ ├── 3. 监督微调【模型优化】
│ │ ├── SFT数据集【训练数据】
│ │ │ ├── 776K训练样本【数据量】
│ │ │ └── 多种解决方案格式【数据类型】
│ │ │ ├── 思维链(CoT)【推理格式】
│ │ │ ├── 程序思维(PoT)【编程格式】
│ │ │ └── 工具集成推理【混合格式】
│ │ └── DeepSeekMath-Instruct 7B【微调模型】
│ │ ├── MATH 46.8%准确率【性能指标】
│ │ └── 超越开源模型【相对性能】
│ │
│ ├── 4. 强化学习【进阶优化】
│ │ ├── GRPO算法【创新方法】
│ │ │ ├── PPO变体【算法基础】
│ │ │ ├── 无需价值模型【效率优化】
│ │ │ └── 组相对优势估计【核心创新】
│ │ │ ├── 基线从组分数计算【技术细节】
│ │ │ └── 减少训练资源【实际效益】
│ │ └── DeepSeekMath-RL 7B【最终模型】
│ │ ├── MATH 51.7%准确率【峰值性能】
│ │ ├── GSM8K 88.2%准确率【基础性能】
│ │ └── 域外性能提升【泛化能力】
│ │
│ ├── 5. 关键发现【经验总结】
│ │ ├── 预训练洞察【数据层面】
│ │ │ ├── 网页数据潜力巨大【正面发现】
│ │ │ ├── arXiv论文效果有限【反直觉发现】
│ │ │ └── 多语言数据有益【数据多样性】
│ │ └── 强化学习洞察【算法层面】
│ │ ├── 统一范式理解【理论贡献】
│ │ ├── 在线vs离线采样【对比分析】
│ │ └── 提升Maj@K而非Pass@K【性能分析】
│ │
│ └── 6. 贡献与局限【总体评价】
│ ├── 主要贡献【正面成果】
│ │ ├── 接近闭源模型性能【性能突破】
│ │ ├── 高效RL算法【方法创新】
│ │ └── 开源社区推动【社区影响】
│ └── 当前局限【待改进点】
│ ├── 几何和定理证明较弱【能力短板】
│ ├── 模型规模限制【资源约束】
│ └── few-shot能力不足【泛化限制】
问1:DeepSeekMath预训练的目的是什么?
答1:让语言模型获得强大的数学推理能力。
问2:怎么让模型获得数学能力?
答2:用大量数学文本训练模型。
问3:数学文本从哪里来?
答3:从互联网Common Crawl中筛选出来。
问4:Common Crawl是什么?
答4:公开的网页存档,包含数十亿个网页的原始数据。
针对数据不足,Common Crawl中藏着大量未被利用的数学内容,但需要精确识别。
问5:怎么从海量网页中筛选数学内容?
答5:用fastText分类器识别数学相关网页。
问6:fastText分类器是什么?
答6:Facebook开发的文本分类工具,能快速判断文本属于哪个类别。
问7:分类器怎么知道什么是数学内容?
答7:先用已知的数学文本(OpenWebMath)训练它,让它学会识别特征。
问8:训练分类器需要什么?
答8:需要正样本(数学文本)和负样本(非数学文本)。
问9:为什么需要负样本?
答9:让分类器学会区分"是数学"和"不是数学"的差异。
问10:训练一次就够了吗?
答10:不够,需要迭代四轮来提高覆盖率。
问11:为什么要迭代?
答11:每轮发现新的数学网站和模式,用新数据改进分类器。
问12:收集到数据后直接用吗?
答12:不,需要去污染,避免包含测试题答案。
问13:为什么要避免测试题?
答13:防止模型"背答案"而非真正理解,影响评估的公平性。
问14:最后用这些数据做什么?
答14:训练DeepSeek-Coder模型500B个token,得到DeepSeekMath-Base。
问15:为什么选择Coder模型作为基础?
答15:代码训练让模型更擅长逻辑推理和工具使用。
核心就是:找数学数据→训练分类器→迭代改进→清洗数据→训练模型。
问:每个缺失怎么对应到具体问题特征?
答:
- 数据问题→模型没见过足够的数学模式
- 指令问题→模型不会按步骤解题
- 优化问题→模型输出不够稳定可靠
为什么要同时用CoT和PoT?
答:CoT适合推理过程,PoT适合计算密集题,两者互补。
针对"不会解题步骤",解法是什么?
答:用776K个标注好的解题过程训练,包含思维链(CoT)和程序思维(PoT)。
1. 按照逻辑关系中文拆解【GRPO解法】
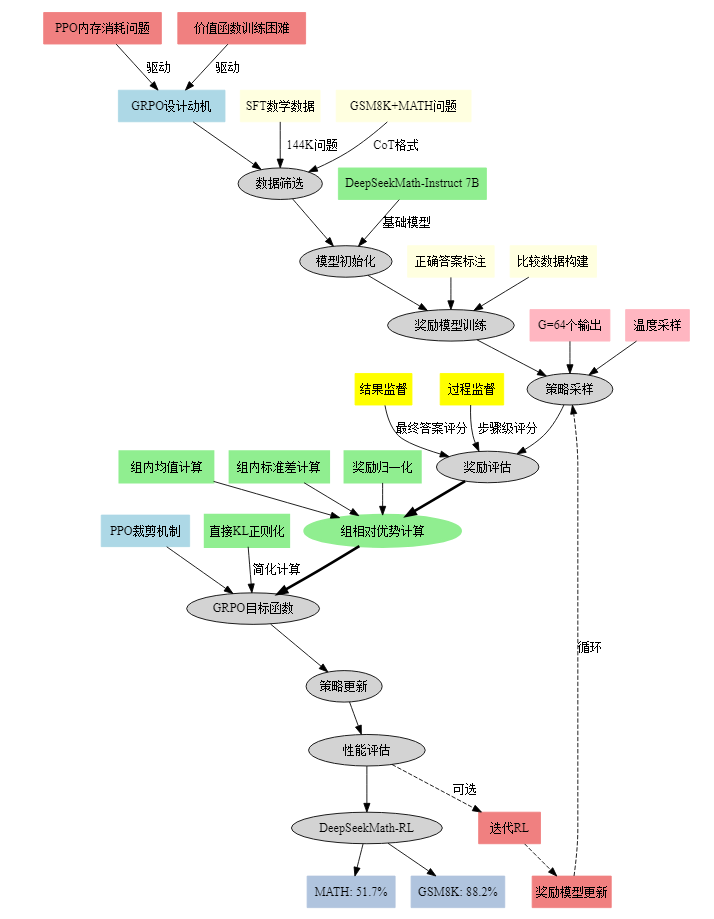
技术拆解(公式形式)
GRPO解法 = 子解法1(组内基线估计法)+ 子解法2(相对优势计算法)+ 子解法3(直接KL正则化法)
子解法1:组内基线估计法
- 公式:使用同一问题q的G个采样输出{o₁, o₂, …, oG}的平均奖励作为基线
- 之所以用组内基线估计法,是因为价值函数训练困难特征(在LLM中通常只有最后一个token有奖励分数,这使得训练准确的token级价值函数变得复杂)
子解法2:相对优势计算法
- 公式:Âᵢ,ₜ = (rᵢ - mean®)/std® (结果监督)或 Âᵢ,ₜ = Σ r̂ⁱⁿᵈᵉˣ⁽ʲ⁾ᵢ (过程监督)
- 之所以用相对优势计算法,是因为奖励模型比较性特征(奖励模型通常在同一问题的不同输出比较数据集上训练,具有比较性质)
子解法3:直接KL正则化法
- 公式:在损失中直接添加KL散度DKL(πθ||πref)而非在奖励中添加KL惩罚
- 之所以用直接KL正则化法,是因为简化计算特征(避免复杂化优势函数Âᵢ,ₜ的计算)
与同类算法的主要区别
与PPO的区别:
- 无需价值模型:GRPO不需要训练额外的价值函数,PPO需要
- 组相对基线:GRPO使用组内平均作为基线,PPO使用学习的价值函数
- 内存效率:GRPO显著减少了训练资源消耗
2. 子解法逻辑链(决策树形式)
GRPO决策树:
│
├─ 是否需要价值函数?
│ │
│ ├─ 否 → 使用组内基线估计法
│ │ │
│ │ ├─ 采样G个输出
│ │ └─ 计算平均奖励作为基线
│ │
│ └─ 是 → 转向PPO(不符合GRPO特征)
│
├─ 如何计算优势?
│ │
│ ├─ 结果监督 → 归一化最终奖励
│ └─ 过程监督 → 累积后续步骤奖励
│
└─ 如何正则化?│└─ 直接KL散度 → 避免奖励中的复杂计算
逻辑关系:链条型 - 三个子解法按顺序执行,前一个的输出是后一个的输入。
3. 隐性方法分析
关键隐性方法:组相对优势估计
通过逐行对比解法发现的隐性步骤:
- 对同一问题采样多个输出(第7行)
- 计算组内奖励分布统计量(第8行)
- 使用统计量进行奖励归一化(第9行)
- 将归一化奖励作为所有token的优势(结果监督)
这个隐性方法的关键在于:将个体奖励转换为群体相对排名,这不是传统强化学习教科书中明确定义的标准步骤。
4. 隐性特征分析
隐性特征:奖励模型的比较性本质
逐行对比发现的隐性特征:
- 论文第13页提到:“The group relative way that GRPO leverages to calculate the advantages, aligns well with the comparative nature of rewards models”
- 这个特征不在问题描述中,而是在解法的第8-9行之间形成的中间状态
- 关键隐性方法定义:比较性优势对齐法 - 利用奖励模型天然的比较性质,通过组内相对排名而非绝对值来指导学习
5. 潜在局限性
- 采样效率依赖性:需要为每个问题采样多个输出(论文中是64个),增加了推理成本
- 组大小敏感性:组内样本数量G可能影响基线估计的稳定性
- 分布偏移脆弱性:当策略显著改变时,组内基线可能不再准确
- 奖励稀疏性限制:在奖励极其稀疏的任务中,组内可能没有正奖励样本
- 泛化能力受限:论文显示GRPO提升了Maj@K但未提升Pass@K,说明可能只是改善了输出分布而非根本能力
6. 多题一解的通用解题思路
通用解题模式:相对比较强化学习范式
共用特征:具有比较性奖励信号的序列决策问题
- 数学推理任务
- 代码生成任务
- 文本生成质量评估任务
解题流程:
- 识别比较性特征 → 判断是否存在同问题多输出比较的可能
- 构建比较群体 → 为每个输入采样多个候选输出
- 相对排名评估 → 使用群体统计量而非绝对值评估优劣
- 梯度权重调整 → 基于相对排名调整参数更新方向
适用题目类型:
- 存在明确正确答案的生成任务
- 可以通过比较判断质量优劣的任务
- 奖励函数具有比较性质的强化学习问题
- 需要降低训练资源消耗的大模型优化场景
核心洞察:通过将个体表现置于群体环境中评估,利用相对位置而非绝对数值来指导学习,这种思路可推广到任何具有比较性评估标准的优化问题。
2. 全流程优化分析
多题一解特征分析
共用特征:比较性奖励评估特征
- 特征名称:相对排名可比较性
- 解法名称:群体相对优势估计法
- 适用题目:数学推理、代码生成、文本质量评估、机器翻译
共用特征:资源受限优化特征
- 特征名称:内存计算约束性
- 解法名称:无价值函数强化学习法
- 适用题目:大模型微调、边缘设备部署、实时交互系统
一题多解分析
针对"减少PPO内存消耗"这一核心问题,存在多种解法:
- GRPO解法(本文)→ 对应特征:奖励比较性 + 内存敏感性
- 简化PPO解法 → 对应特征:模型压缩性 + 梯度累积性
- 离线RL解法(如DPO)→ 对应特征:数据静态性 + 偏好可比性
- 蒸馏学习解法 → 对应特征:知识传递性 + 模型轻量性
更优解法探索
发现的隐性特征:奖励信号的时序依赖性
- 当前GRPO将所有时刻的优势设为相同值(结果监督)
- 优化方向:引入时序权重衰减,近期步骤获得更高权重
更直接的特征:样本效率vs计算效率权衡
- 当前解法:固定采样64个候选
- 优化解法:自适应采样量 - 根据奖励方差动态调整采样数
替换解法优化:
原始环节:固定组大小G=64
↓ 优化
自适应组大小:G = max(8, min(64, 2×std(previous_rewards)))原始环节:简单奖励归一化
↓ 优化
稳健归一化:使用中位数和四分位距代替均值和标准差原始环节:每步相同优势值
↓ 优化
时序加权优势:Â_t = normalized_reward × decay^(T-t)
3. 医疗领域应用示例
输入输出定义
输入:医疗诊断推理问题
问题:患者男性,45岁,主诉胸痛3小时,伴出汗、恶心。
心电图显示ST段抬高。肌钙蛋白升高。
请给出诊断和治疗建议。
输出:结构化医疗推理答案
诊断推理:
1. 根据ST段抬高+肌钙蛋白升高 → 急性ST段抬高型心肌梗死
2. 胸痛+出汗+恶心 → 典型心梗症状三联征
3. 中年男性 → 心血管疾病高危人群治疗建议:
1. 立即急诊PCI或溶栓治疗
2. 双抗血小板聚集治疗
3. β受体阻滞剂+ACEI类药物
4. 他汀类调脂治疗
医疗GRPO全流程
- 问题收集:从医学教材、病例库收集诊断推理题
- 专家标注:多位医生对答案质量评分(1-10分)
- 模型采样:为每个病例生成64个诊断方案
- 医疗奖励模型:基于诊断准确性+治疗合理性训练
- 组相对评估:同一病例的64个方案内部排名
- 优势计算:(个体得分 - 组平均分) / 组标准差
- 策略更新:提升高分方案概率,降低低分方案概率
- 迭代优化:根据新的医疗知识更新奖励模型
关键优势:
- 安全性:通过组内比较避免生成极端错误的医疗建议
- 一致性:确保同类病例的诊断逻辑保持一致
- 效率性:避免训练复杂的医疗价值函数,降低计算成本
潜在风险:
- 如果组内样本都存在系统性偏误,相对排名仍可能导致错误诊断
- 需要高质量的医疗奖励模型,否则会放大医疗错误
