Deep Unfolding Net(LR到HR)
论文
Zhang, Kai et al. "Deep Unfolding Network for Image Super-Resolution",Computer Vision and Pattern Recognition (2020): 3214-3223.
Deep Unfolding 基于MAP最大后验概率框架来做
原论文也是求解低分辨率到高分辨率图像问题
由贝叶斯原理,高分辨率图像(HR)表示为x,低分辨率图像(LR)表示为y,实际求解时P(y)为常数,求解低分辨率到高分辨率图像问题转化为最大化后验概率P(x|y)= P(y|x)P(x)问题,x经过退化后与y越一致,P(x|y)越大:
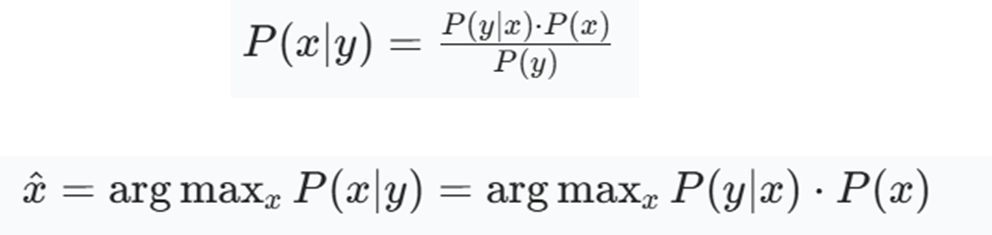
由于概率乘积的最大化等价于 “负对数概率之和的最小化”(对数函数为单调递增函数,负对数可将乘积转化为求和、最大化转化为最小化),论文将 MAP 目标进一步转化为能量函数最小化问题:
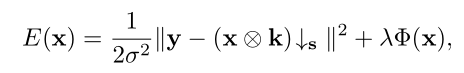
该函数包含两个耦合的目标:“数据保真项”(第一项,确保x经退化后贴近 LR 图像y)和 “先验项”(第二项,确保x符合自然图像规律);直接优化x需同时满足两个目标,数学上无闭式解(无法通过简单矩阵运算求解),只能通过复杂数值迭代逼近,且效率低、参数调优困难 —— 这也是传统模型驱动方法的核心缺陷。
为解决这一问题,论文采用HQS 算法,通过引入辅助变量z(可理解为 “HR 图像x的中间估计草稿”),将上述公式的单目标优化拆分为下面公式的双变量优化,实现 “分而治之” 的求解思路。