人工智能之数学基础：离散随机变量和连续随机变量

本文重点

随机变量是概率论与统计学中的核心概念，用于将随机现象的抽象结果转化为可量化的数值。根据取值特性的不同，随机变量可分为离散型和连续型两大类。

在前面的课程中我们学习了随机变量，随机变量可以理解为一个函数，通过这个函数我们就可以将随机试验中的结果数值化了，随机变量有两种类型，一种类型是离散型随机变量，另外一种类型是连续型随机变量。

随机变量的类型

离散型随机变量

离散型随机变量是指其可能取值为有限个或可数无限个的随机变量。其取值可以按一定次序一一列出，例如掷骰子的结果（1至6）、某商店一天内的顾客数量（0,1,2,…）等。

核心特性：

• 可列性：取值范围为可数集，如自然数或有限个具体数值。
• 概率质量函数（PMF）：通过概率质量函数描述每个可能取值的概率，满足：

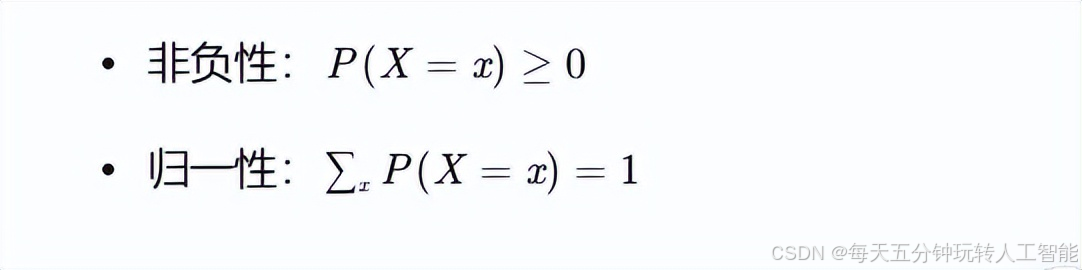
连续型随机变量