Games 101 第四讲 Transformation Cont（视图变换和投影变换）

三维变换

三种变换

下面分别是放缩，旋转，平移


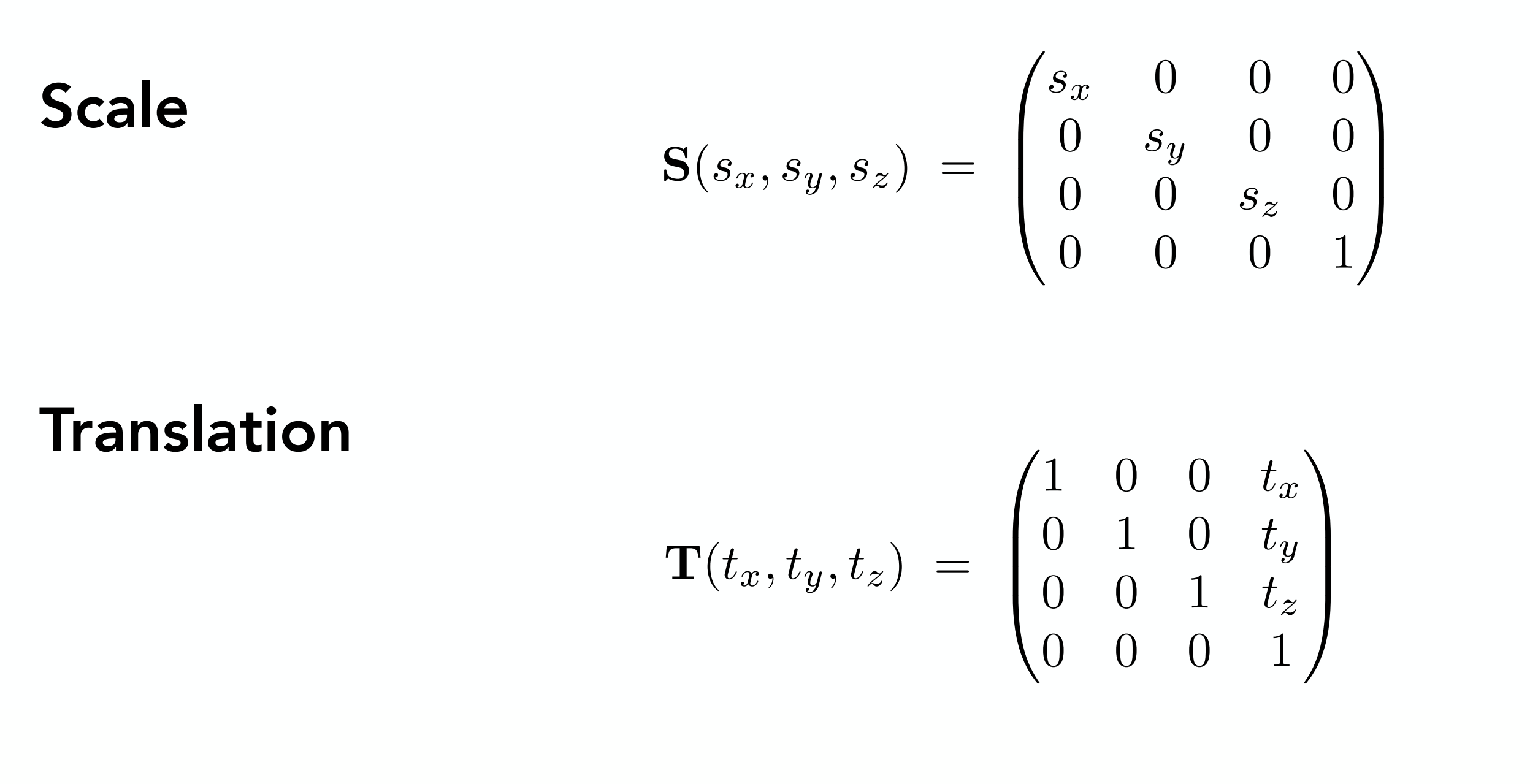
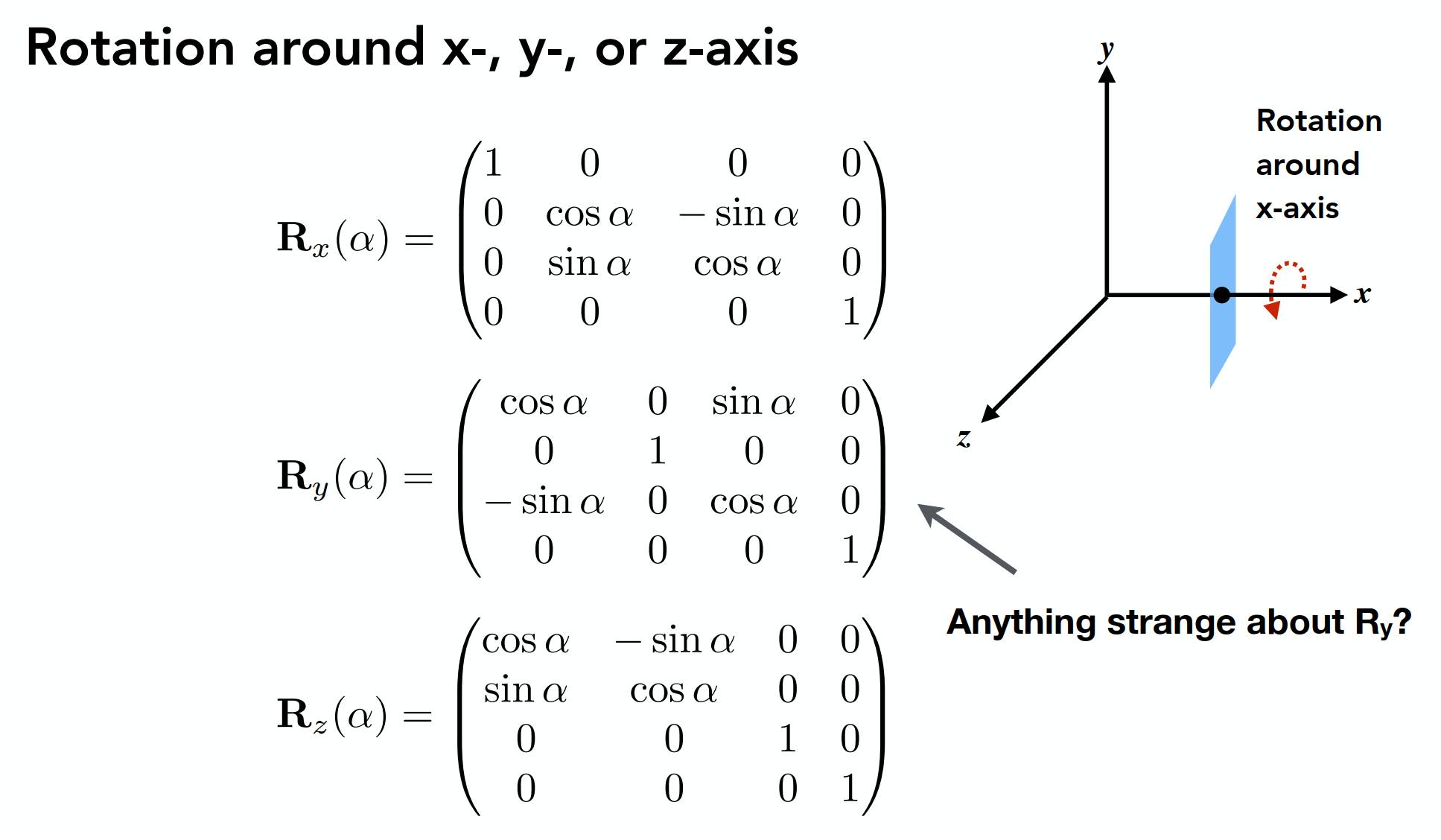
在旋转当中，绕着y轴旋转矩阵的顺序不一样，因为绕着y轴转在右手坐标系中
，z是第一轴，x是第二轴，而负号会加在第一轴上，因此负号在下面。

罗德里格斯公式

旋转能够分解成绕三轴旋转的组合，如图：

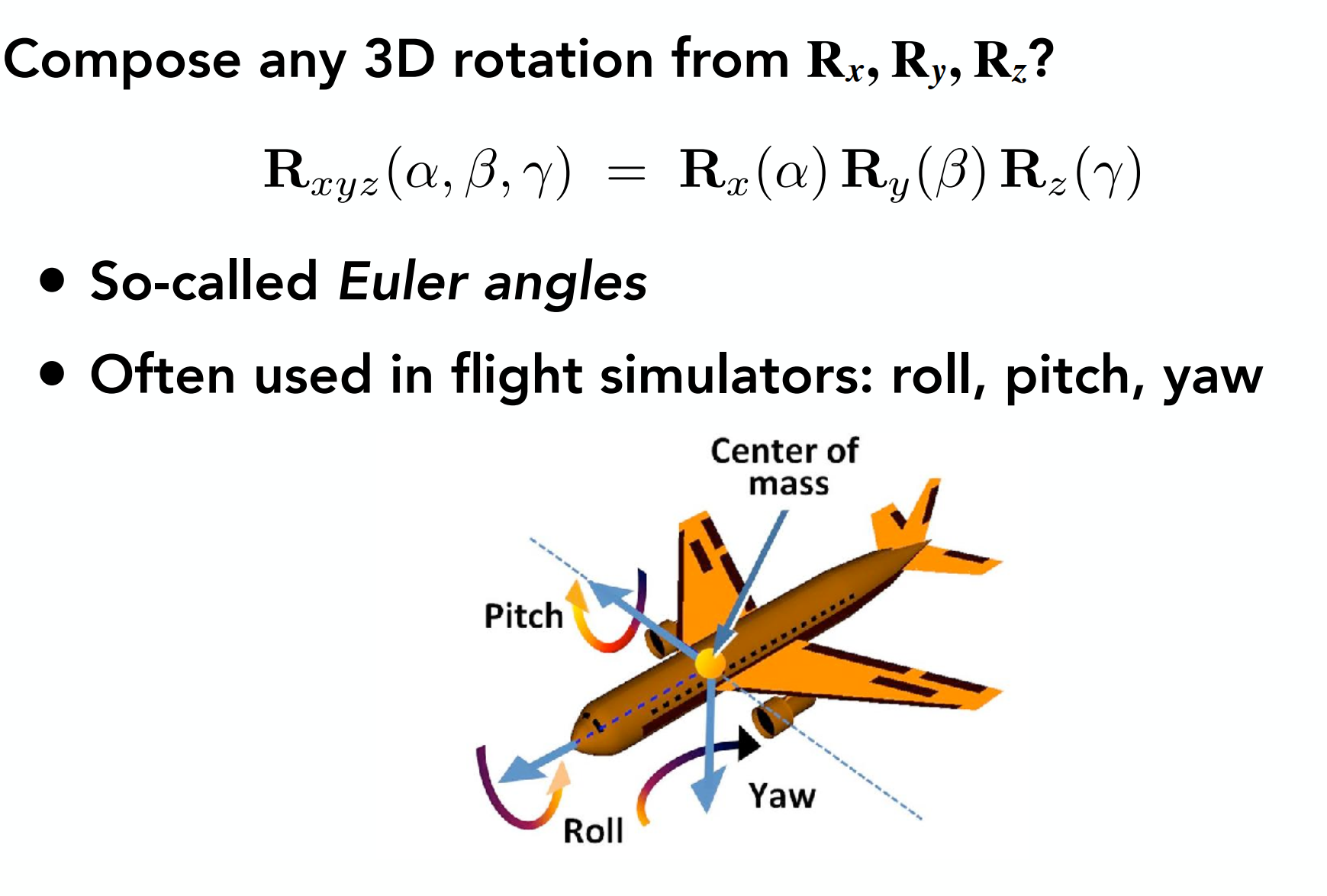
而罗德里格斯公式给出的是绕任意轴旋转的公式：

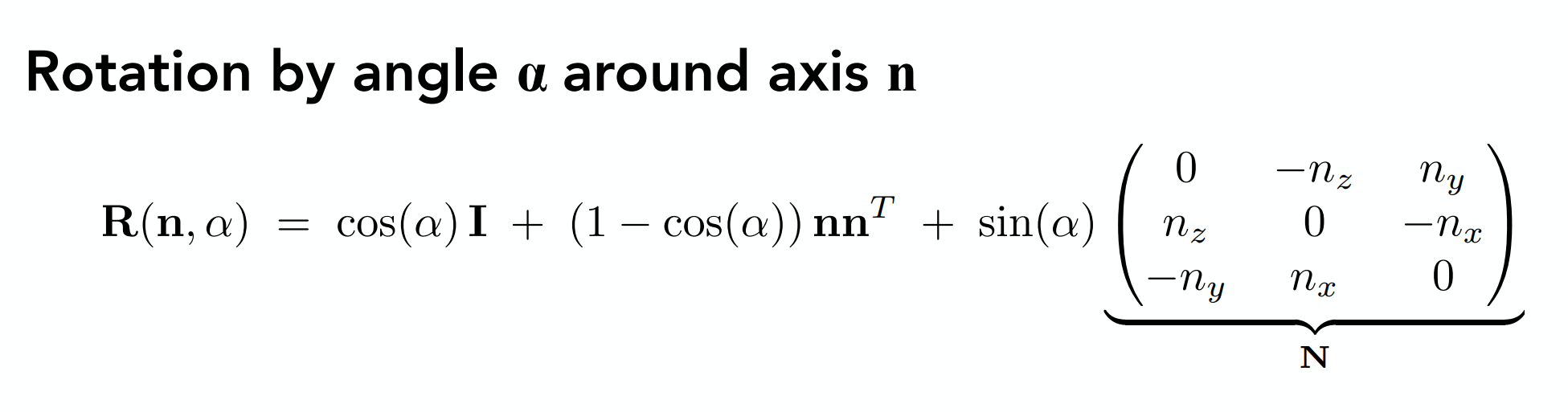
另外，旋转矩阵并不方便做插值：15°的旋转矩阵与25°的旋转矩阵相加除二并不是20°，因此引入了四元数。

相机原理

此部分原Games101没有，为更好展示变换场景引入：

相机成像

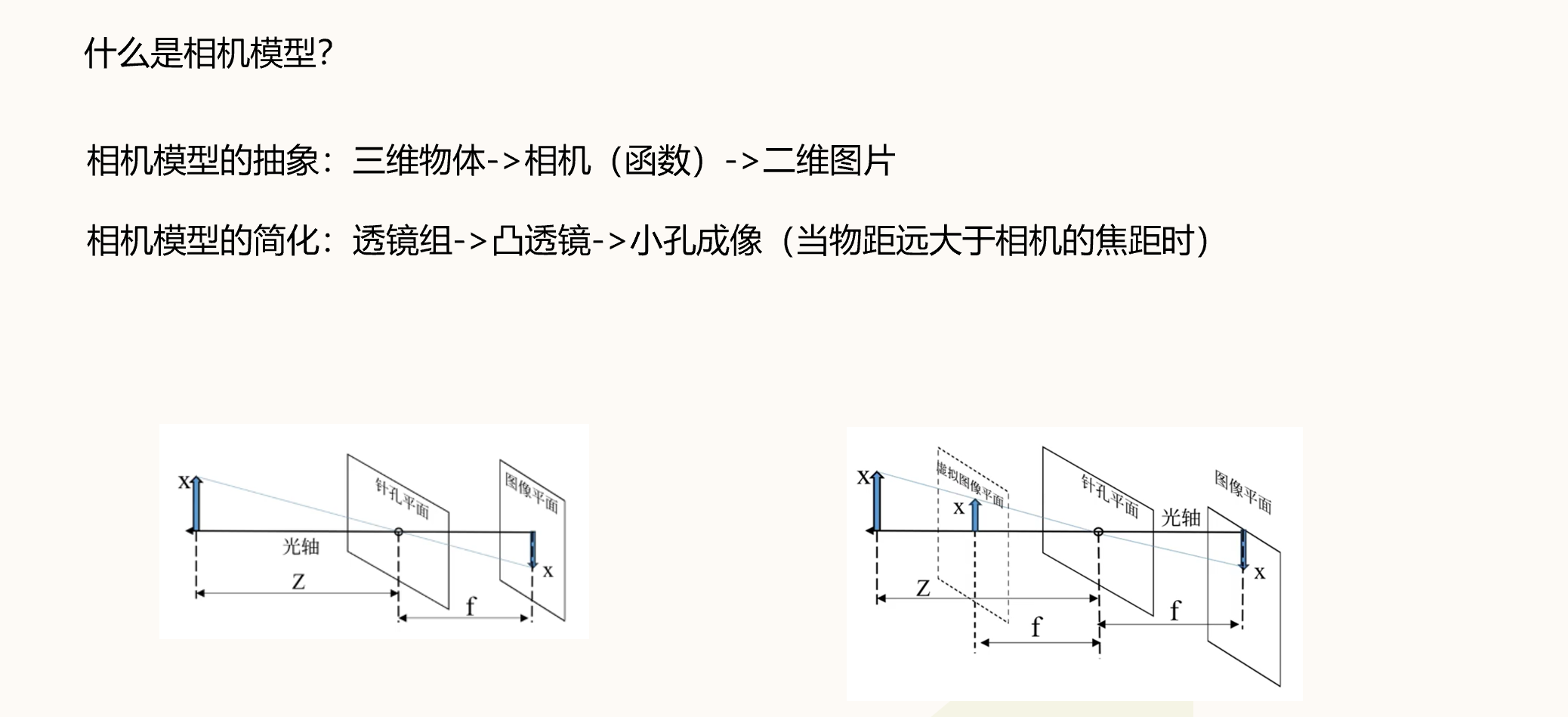
由上图所示，相机模型可以看成小孔成像模型，而为了方便研究，一般将成像面对称放到光心的前面，也就有了下图：

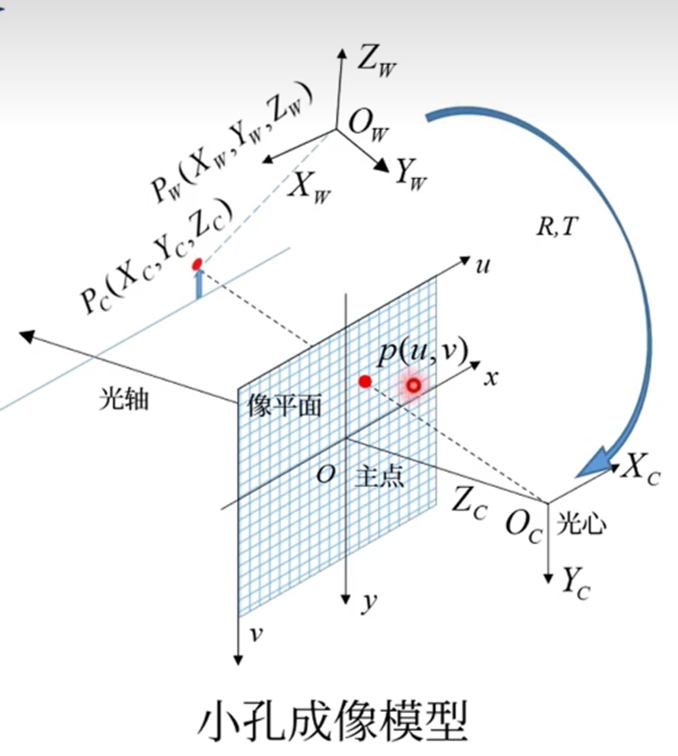
四大坐标系

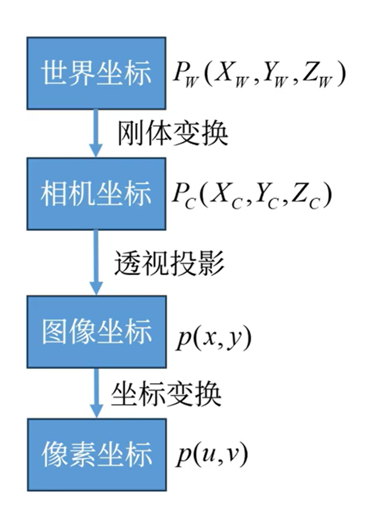
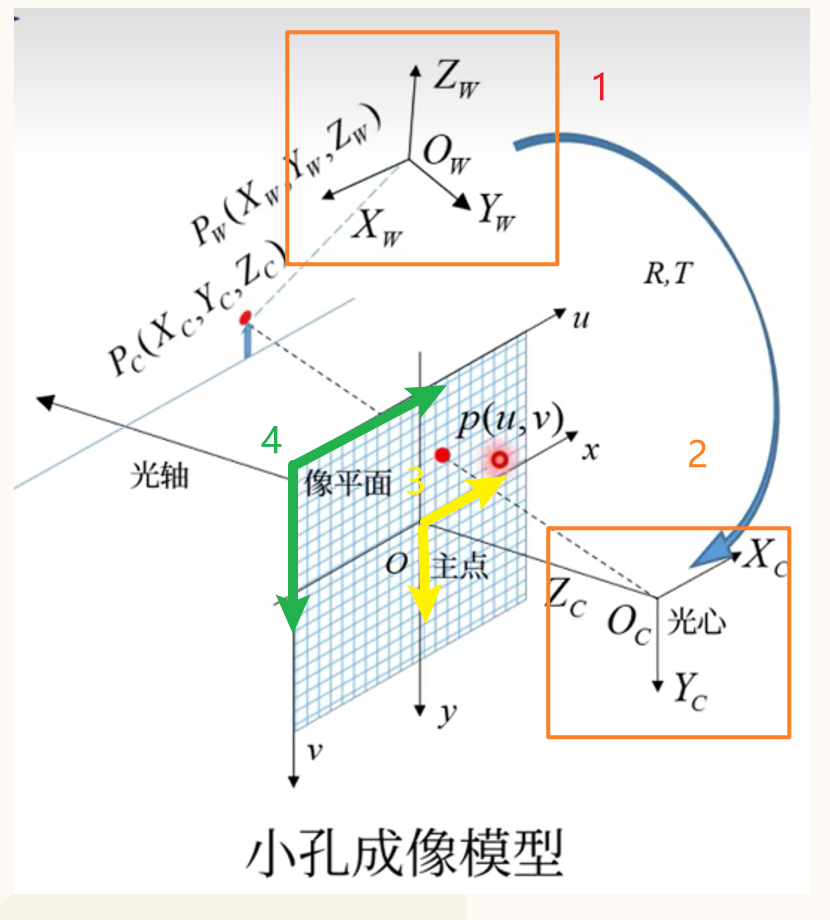
四大坐标系与图中的编号一次对应

刚体变换（世界坐标->相机坐标）

刚体变换在图形学中也称观测变换：
我们一般用三个向量描述摄像机的方向：

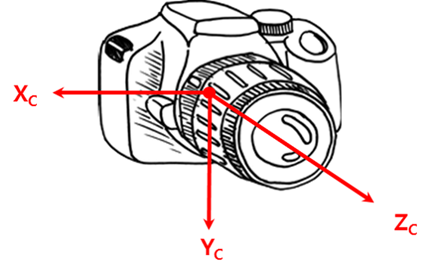
已知在世界坐标系下的位置和方向，将相机坐标坐标系原点即可完成观测变换。

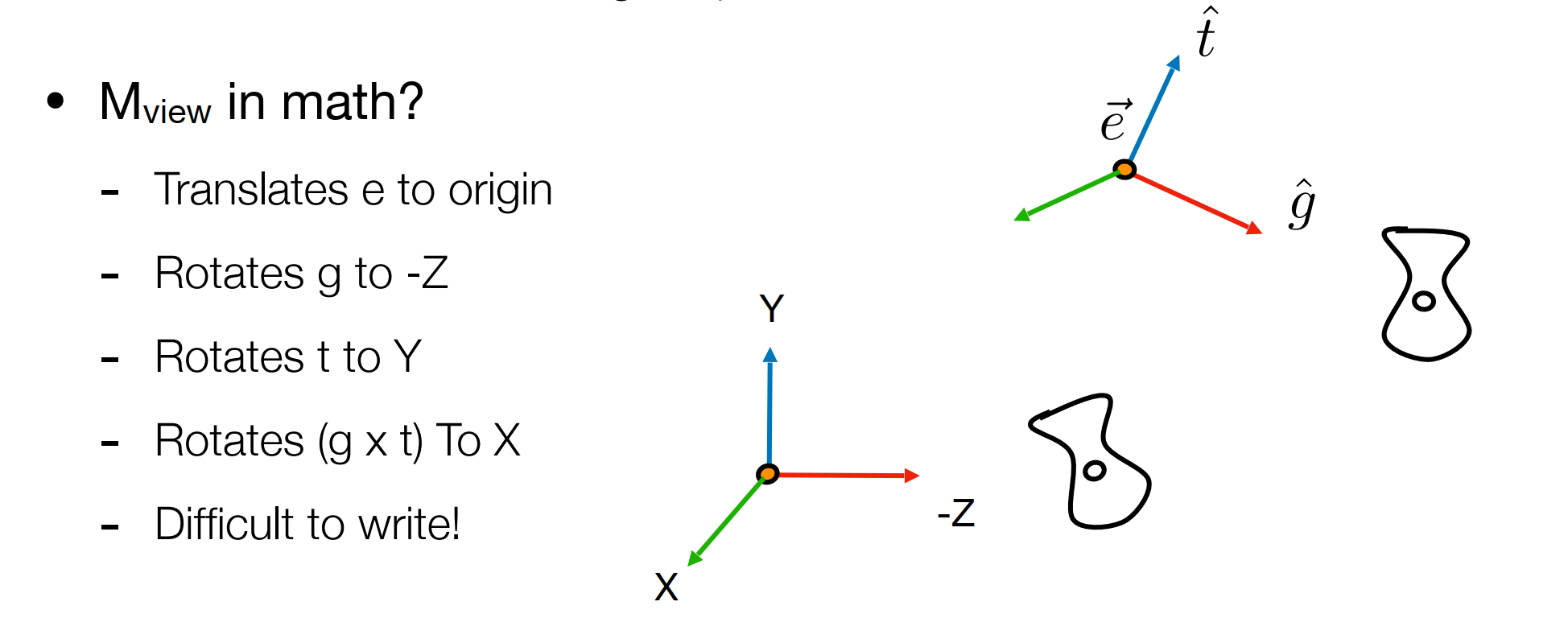
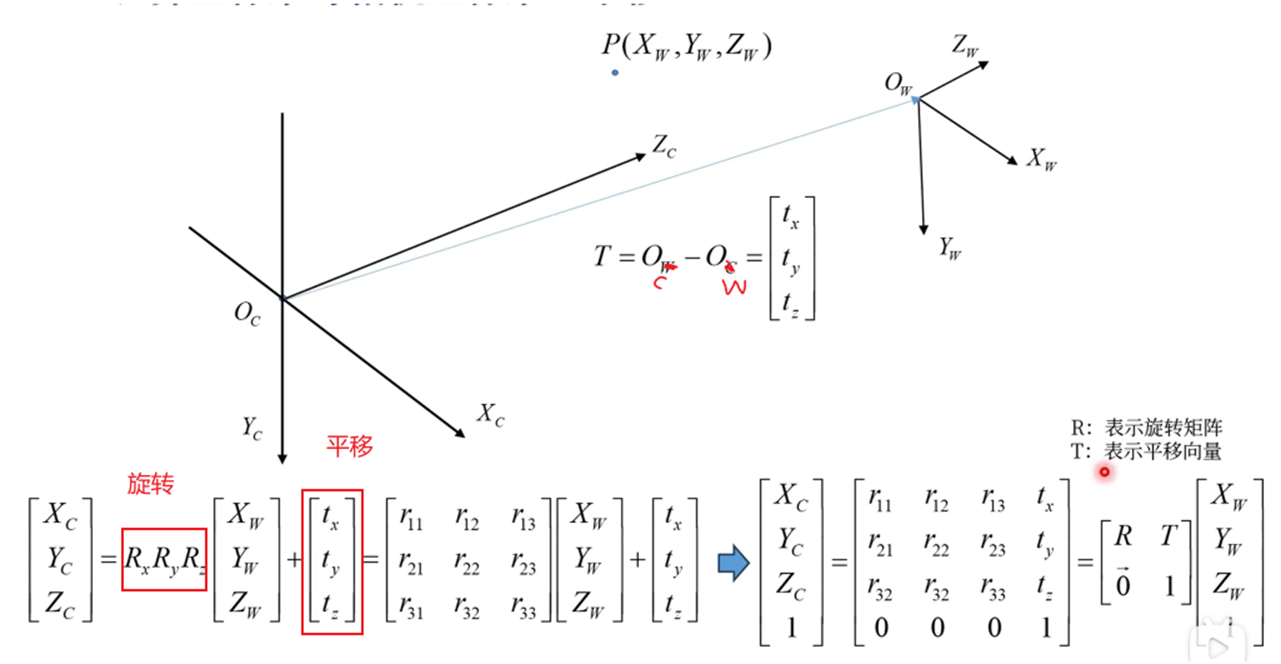
首先完成位置变换：先平移

然后完成旋转：再旋转

为方便先求旋转矩阵的逆变换，在逆变换中x，y，-z三条轴均会变成摄像机方向的三个向量。又由于是正交矩阵（因为是刚体变换），矩阵的逆就是矩阵的转置，由此求出。

透视变换与正交变换

由于摄像机其实是小孔成像（跟人眼一样），因此会有近大远小。

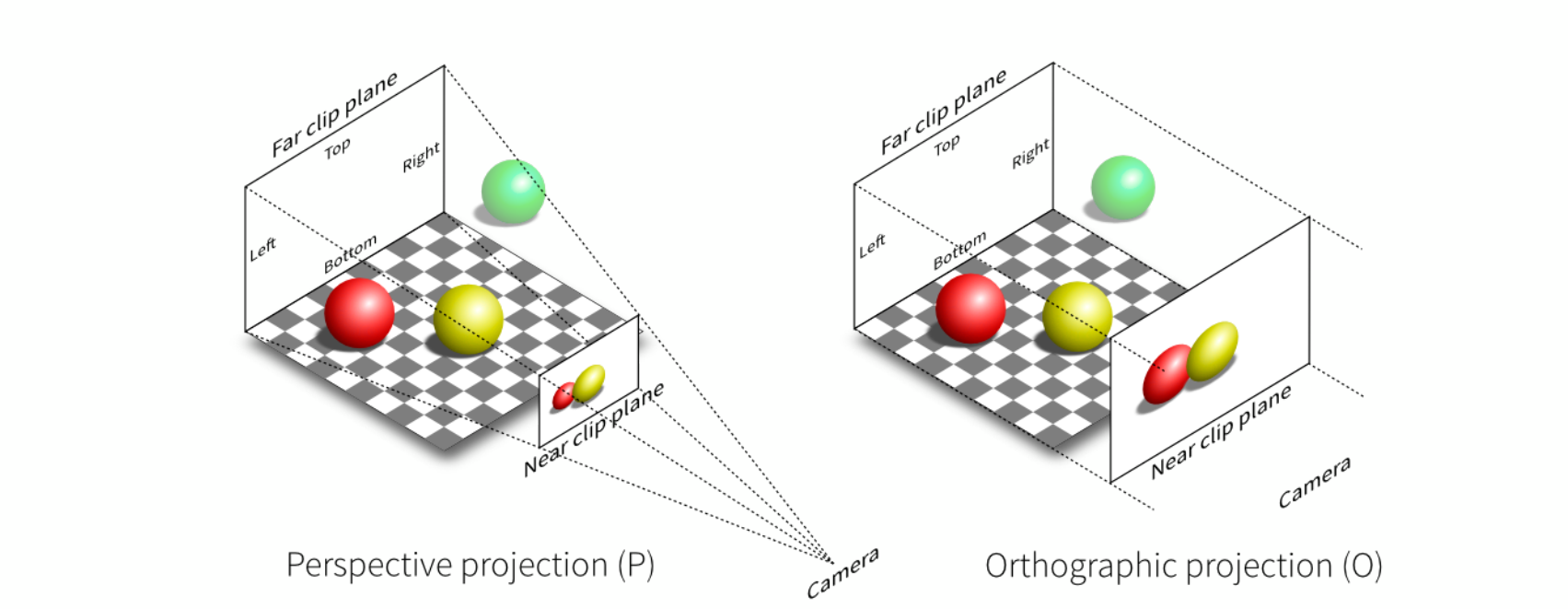
上图中两球大小相等，但在透视投影下大小由差异，而在正交投影下相同。
这是由于透视投影不同位置的光线进入光心的方向不同，不是平行的。

正交变换

在说明透视变换前先需要说明正交变换

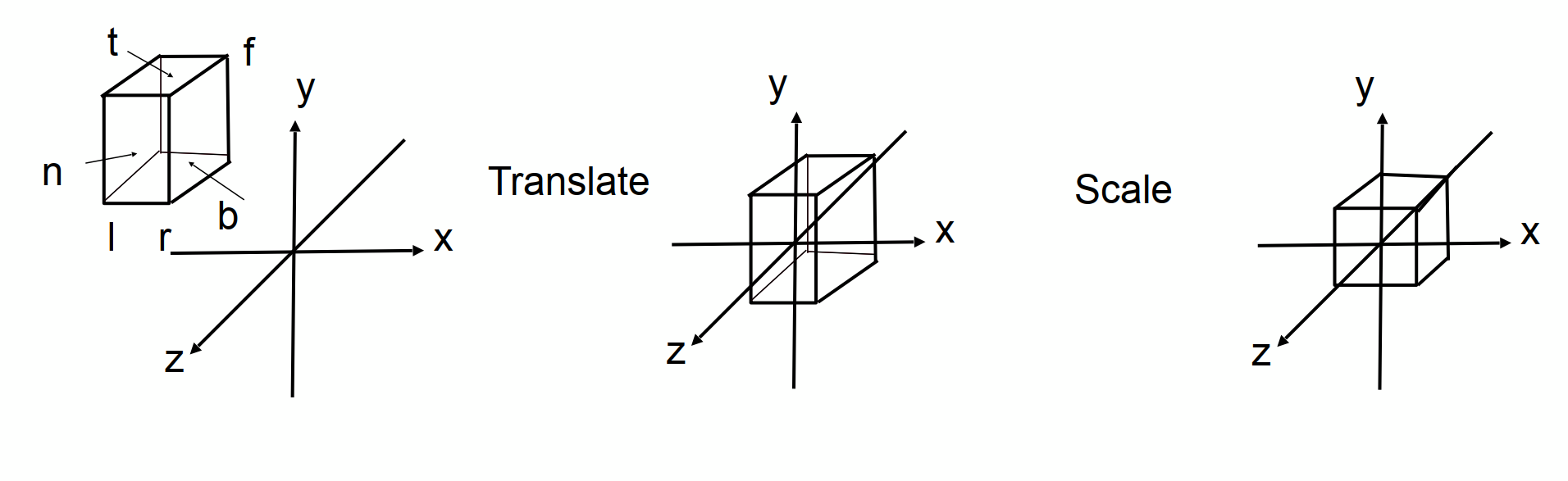
如图所示，正交变换要做的事情其实是将要投影的空间压缩成一个以原点为中心，边长为2的立方体。
由此，定义空间的前后，左右，上下三组数据如图所示，可得到如下的矩阵：

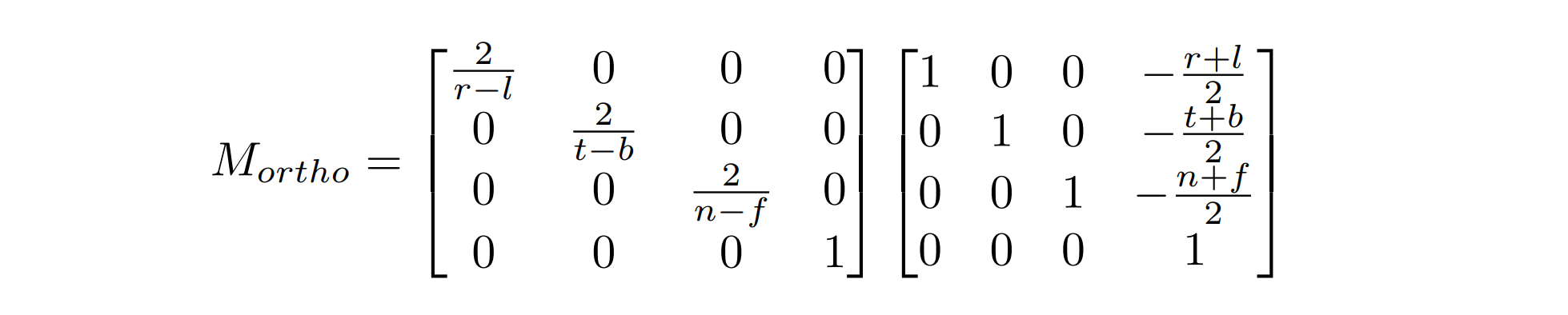
注意，由于z轴是负的，前后的顺序是颠倒的。

投影变换

我们采用改良正交投影的方法实现透视投影。

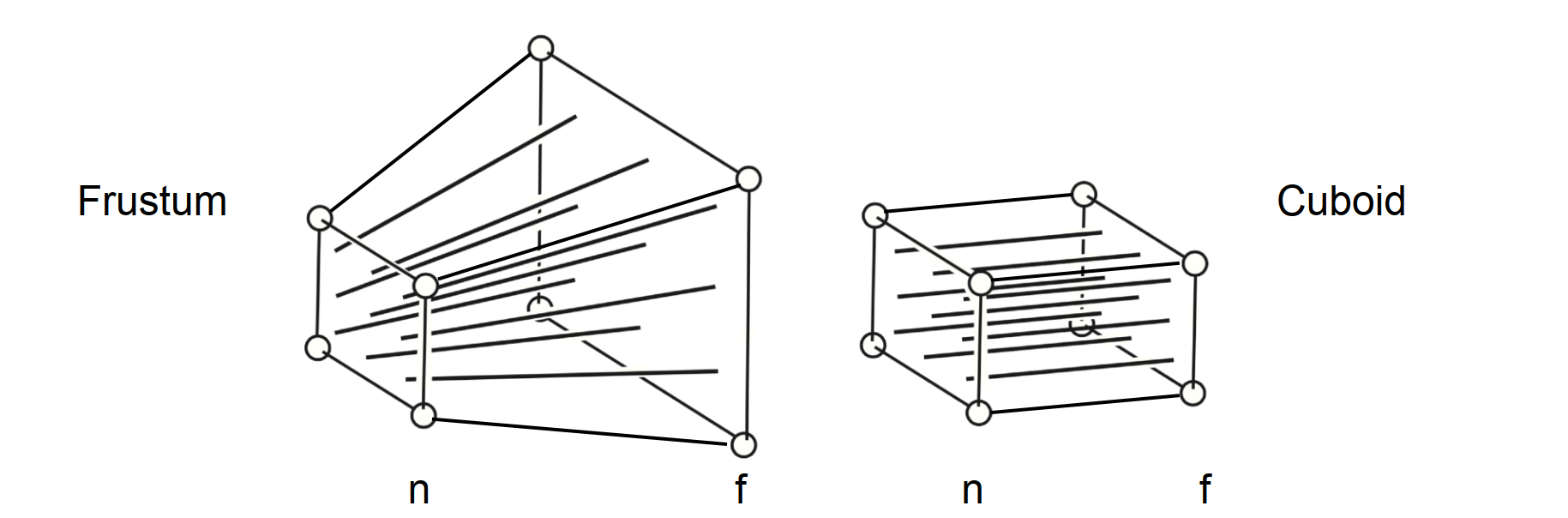
如图所示，我们将原来是视锥的透视投影压成一个长方体，也就是正交投影。
但是压缩的方式不唯一，也就是不确定能压成哪一个长方体。
因此在压缩前需要确定几个参数：

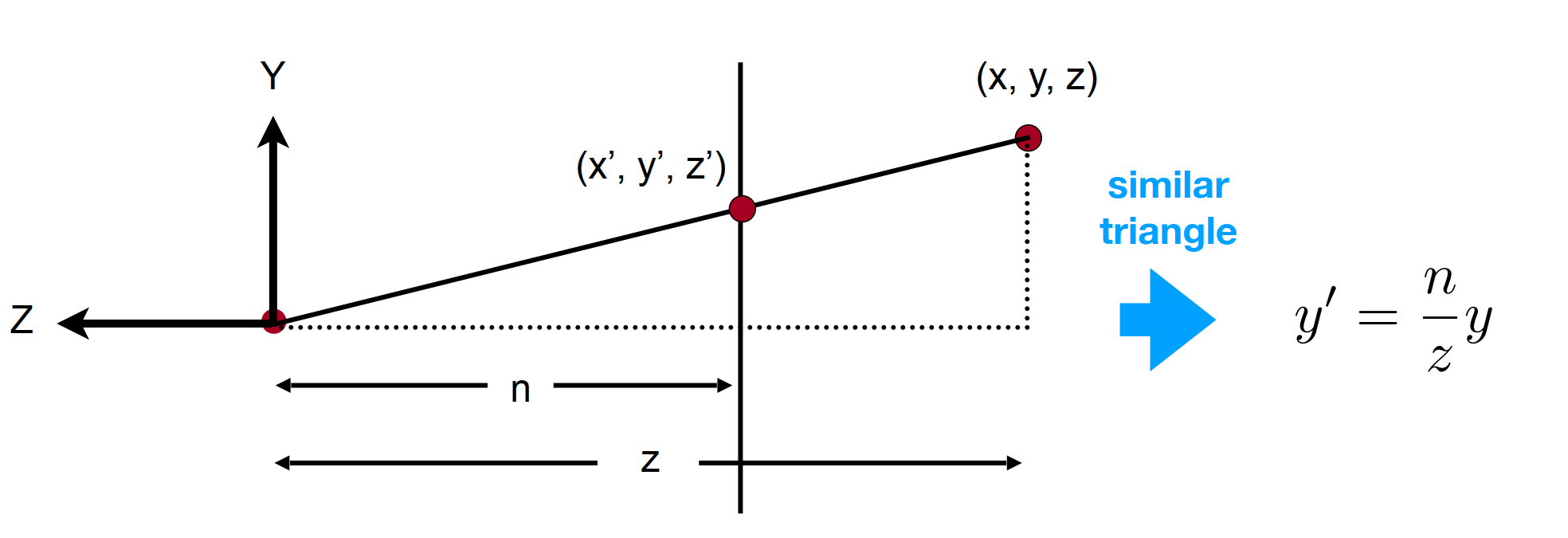
首先要确定两个平面，近平面和远平面，知道这两个平面与原点的距离，分别为n和f。
然后确定这两个平面的性质，近平面变换前后位置不变大小不变，原平面位置不变。
由此，我们列出以下式子：

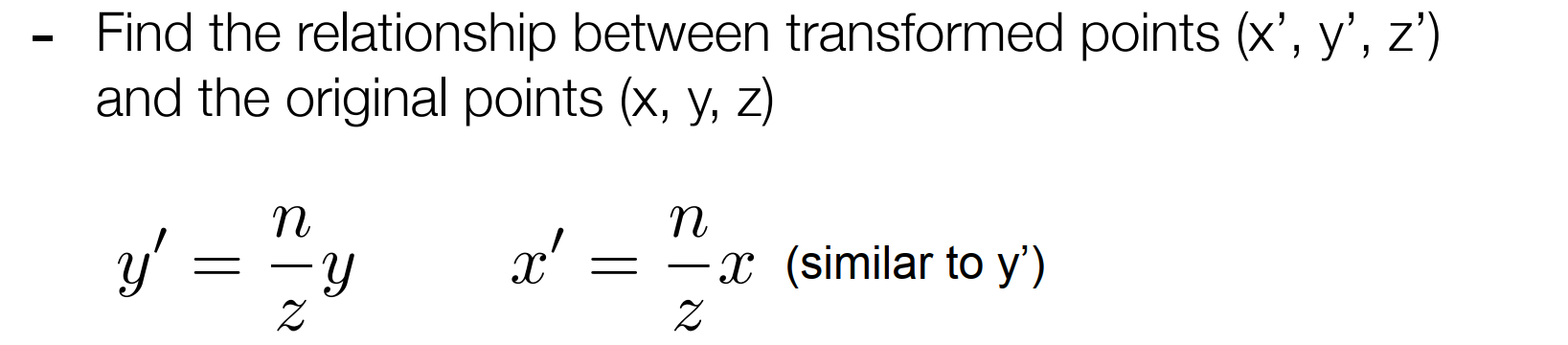
这里的z其实是n到f的任意一值

这样就确定了这个矩阵的三行。
这一步利用的条件是变换后远离近处的平面会变得和近处的平面一样大（x，y方向上）。
然后，再利用近处的平面不变：将n带入z

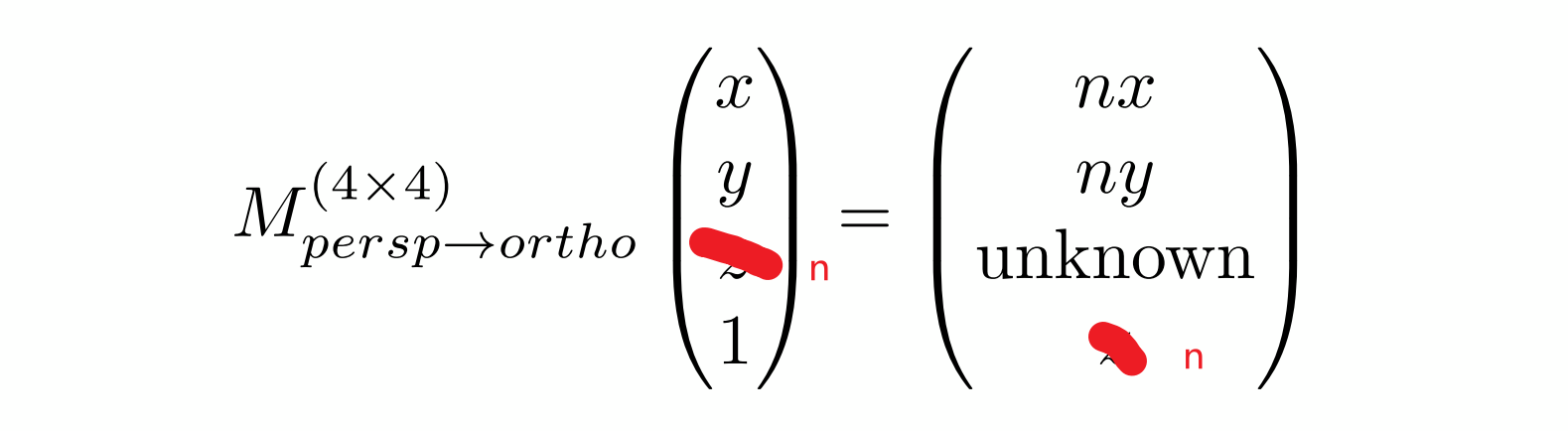
推断出在近处，unknow是$n^2$,由此：

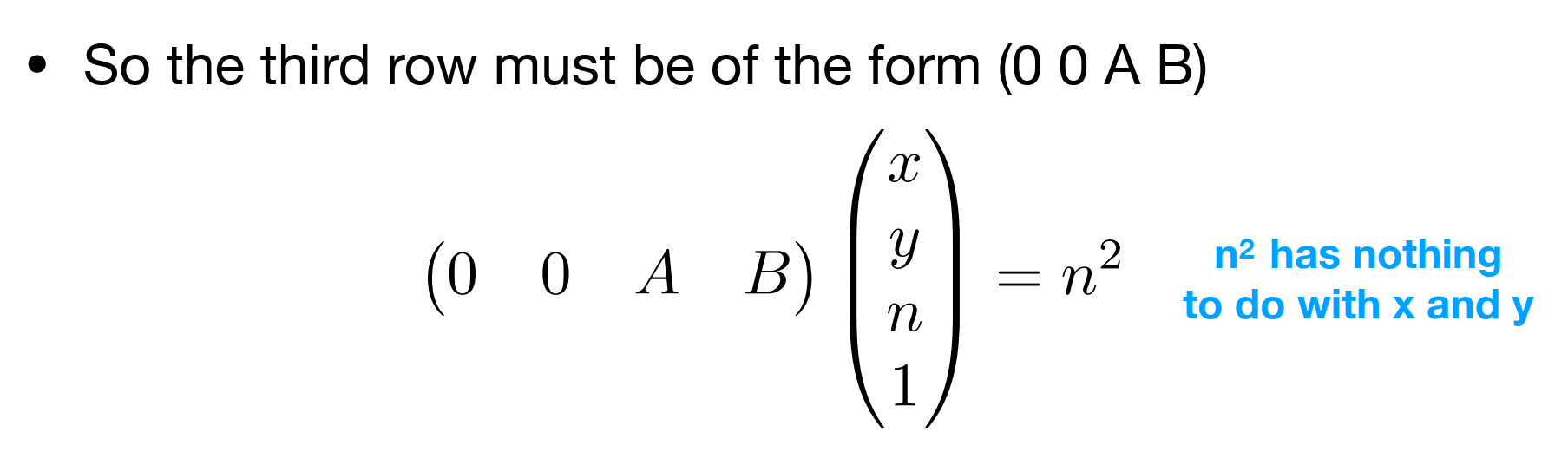
再由远平面中心不变得：



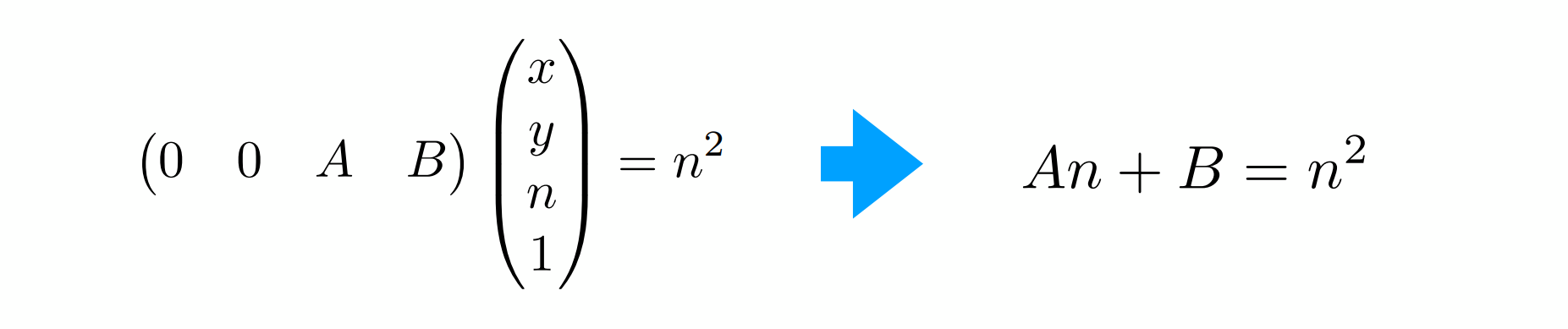
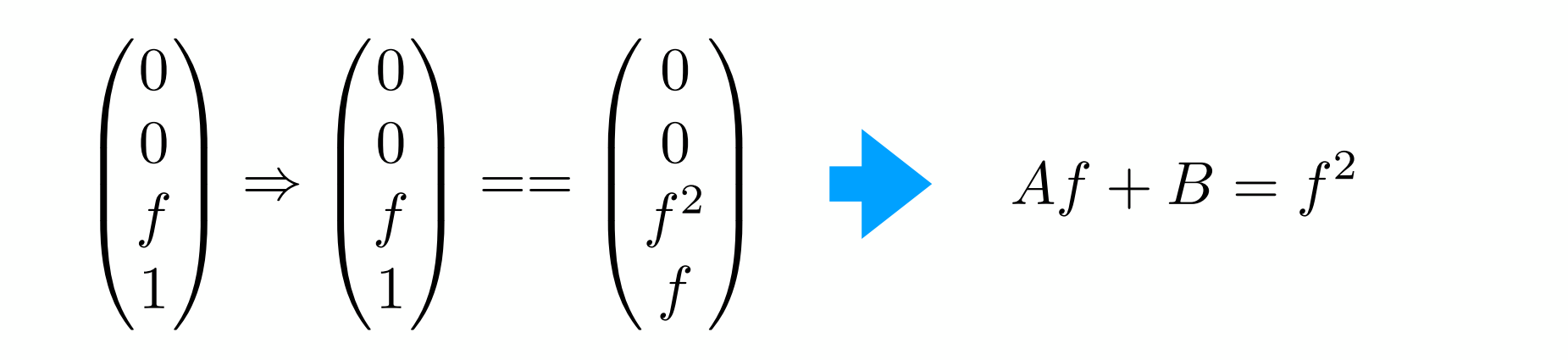
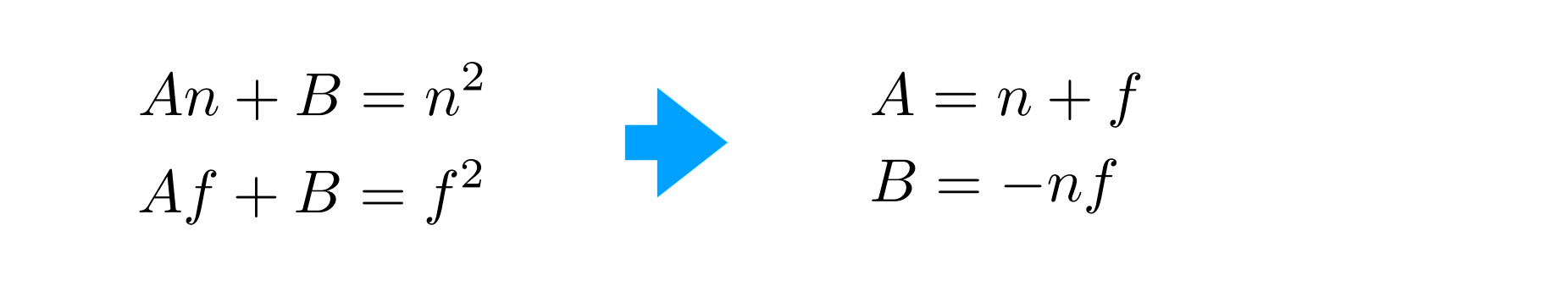
得：

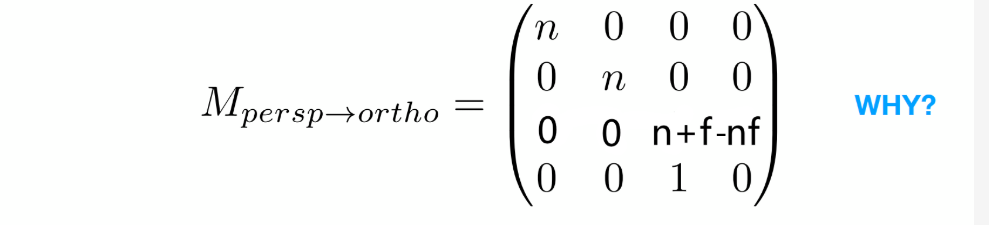
然后再进行正交投影。