算法概述篇
目录
文章目录
前言
一、算法是什么?
二、算法复杂性分析
1.时间复杂性T(n)
1.1渐近复杂性
1.2渐近记号
2.空间复杂性S(n)
常见情况
三、NP完全性理论
1.基本概念
2.一些典型的NP完全问题
总结
前言
注意:此后将更新有关算法分析与设计的相关知识点和练习,大家可以关注一下,敬请期待下一集~
本篇文章将主要讲述有关算法的基本概念还有分析方法,将从五个部分来分别讲述,有任何疑问和建议欢迎大家在评论区留言~
一、算法是什么?
算法是指解决问题的一种方法或者一个过程
算法是若干指令的有穷序列,满足以下性质:
- 输入:有外部提供的量作为算法的输入
- 输出:算法产生至少一个量作为输出
- 确定性:组成算法的每条指令都是清晰,无歧义的
- 有限(穷)性:算法种每条指令的执行次数是有限的,执行每条指令的时间也是有限的
注意:这里算法的第四条性质是与程序的重要区别,程序可以是无穷的,比如你自己写了一个死循环~
二、算法复杂性分析
算法复杂性=算法所需要的计算机资源
1.时间复杂性T(n)
影响时间复杂度的因素:问题规模n,输入序列I,算法本身A
1.1渐近复杂性
概念:设算法的运行时间为T(n),如果存在T*(n),使得,当n趋近于∞时,就称T*(n)为算法的渐近性态或渐近(时间)复杂性
秒杀口诀:要求渐近复杂性,就取最高次项
这里我们来举个例子:
已知算法的运行时间为T(n)=2n^3+5n^2+n+9,利用高等数学的知识我们得知当n趋于0时,低次幂除以高次幂取极限为0,如果我们想要整体极限为0,则T*(n)中必须有T(n)中的最高次项,这里我们不用考虑系数,则T*(n)=n^3
1.2渐近记号
- 渐近上界记号(O):若存在两个正数c和n0,使得n>=n0,都有0<=T(n)<=cf(n),则称T(n)=O(f(n)),即f(n)是T(n)的上界
这里f(n)一般取T(n)的最高阶,这里最简单的一个办法就是把T(n)中所有阶都升高到最高阶,此时每一项的系数之和=c,f(n)=最高阶,取n0=1时即使得T(n)=cf(n)
eg:2n^2+4n<=2n^2+4n^2=6n^2
即T(n)=O(n^2)
- 渐近下界记号(Ω):若存在两个正数c和n0,使得n>=n0,都有T(n)>=cf(n)>=0,则称T(n)=Ω(f(n)),即f(n)是T(n)的下界
这里有一个小tips就是去掉其他多余项,只保留最高项,此时最高项的系数=c,f(n)=最高阶,取一个满足条件的n,令n0=n
eg:T(n)=7n^3+5n^2+8n>=7n^3,此时我取n=1,满足条件,则我可以直接令n0=n=1
即T(n)=Ω(n^3)
- 渐近精确界记号(⊝):通俗来讲就是同时满足既是T(n)的渐近上界又是T(n)的渐近下届的函数
秒杀口诀:要求渐近精确界,就取最高次项
注意:上述的方法都是如何求得一些界的简单方法,只要是符合概念的都可以是T(n)的界,在判断的时候要特别注意
2.空间复杂性S(n)
空间复杂性指的是算法在运行过程中临时占用的存储空间大小。(可以理解为算法需要多少额外的“内存”才能完成任务。)
比如计算时需要用到的变量、数组、数据结构等占用的空间。
常见情况
- O(1): 算法只需要固定大小的空间,与输入数据规模无关。比如交换两个变量的值。
- O(n): 算法需要的空间与输入数据规模成正比。比如需要存储一个长度为n的数组。
- O(n²): 算法需要的空间与输入数据规模的平方成正比。比如需要存储一个n×n的矩阵。
三、NP完全性理论
1.基本概念
- P类问题:可以在多项式时间内求解的判定问题
- NP类问题:非多项式时间内可解的判定问题。即目前没有多项式时间解决的算法,但是如果给出一个候选答案,可以在多项式时间里验证这个答案是不是正确。
- NPC(NP完全问题):满足两个性质:
- 可以在多项式时间验证候选答案(是NP问题)
- 任何一个NP问题可在多项式时间内规约到该问题
- NP—Hard:任何一个NP问题可在多项式时间内规约到该问题,但无法证明问题本身是NP问题。NP—Hard至少和NP问题一样难。
大家如果觉得上面的过于复杂则记住下面这张图即可
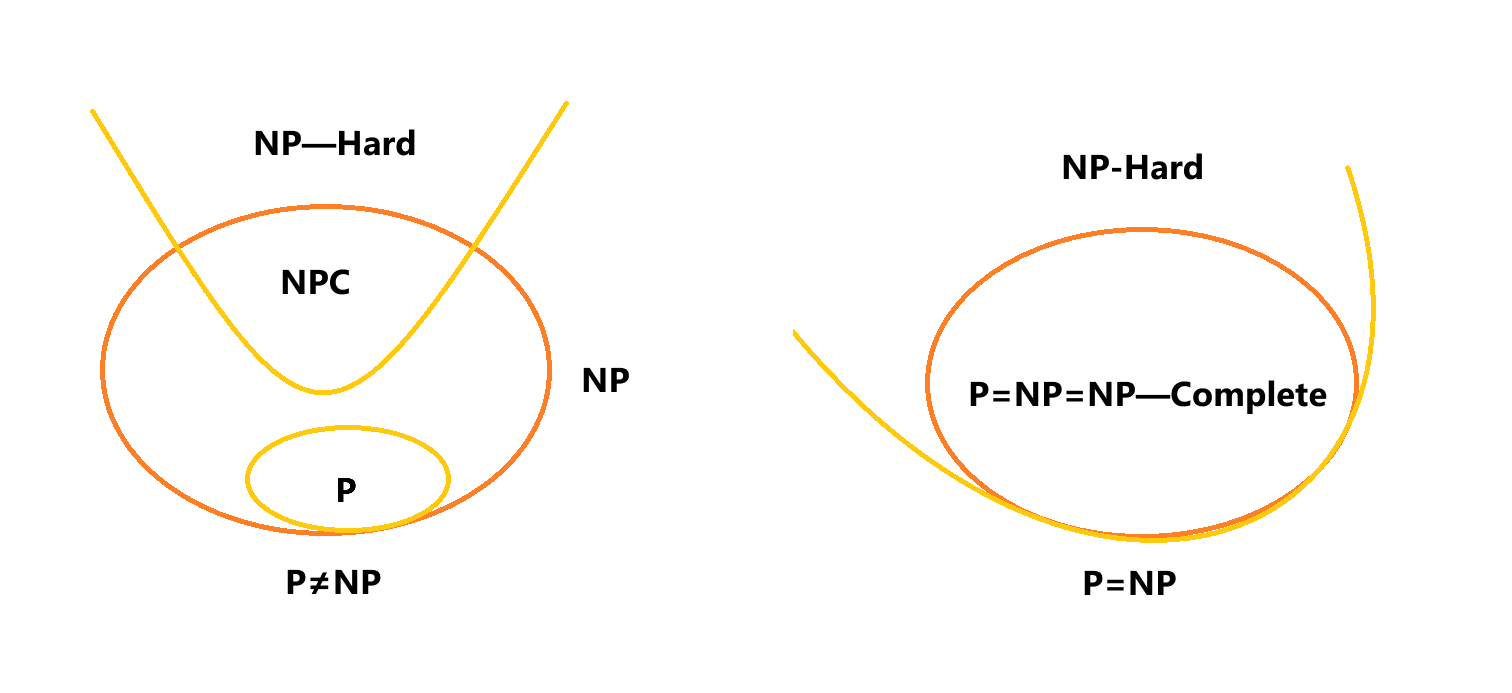
2.一些典型的NP完全问题
- 布尔表达式的可满足问题
- 合取范式的可满足问题
- 三元合取范式的可满足问题
- 哈密顿回路问题
- 旅行售货商问题
- 团问题
- 顶点覆盖问题
- 子集和问题
总结
本文系统介绍了算法的基本概念、时间与空间复杂性分析方法,以及NP完全性理论的核心内容,为算法学习提供了基础框架。下一期将详解分治算法的设计思想与经典案例。
