人工智能机器学习入门——线性回归
一、机器学习概述
什么是机器学习?(Machine Learning)
机器学习是一种实现人工智能的方法。
从数据中寻找规律、建立关系,根据建立的关系去解决问题。
机器学习是机器从数据中自动分析获得模型,并利用模型对未知数据进行预测。
二、机器学习类别
- 监督式学习
- 无监督式学习
- 半监督式学习
- 强化学习
- 生成式 AI
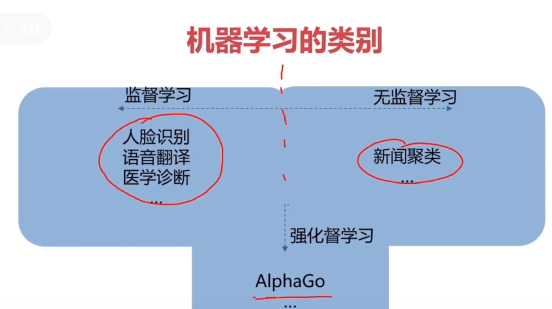
监督学习
- 线性回归
- 逻辑回归
- 决策树
- 神经网络、卷积神经网络、循环神经网络
无监督学习
- 聚类算法
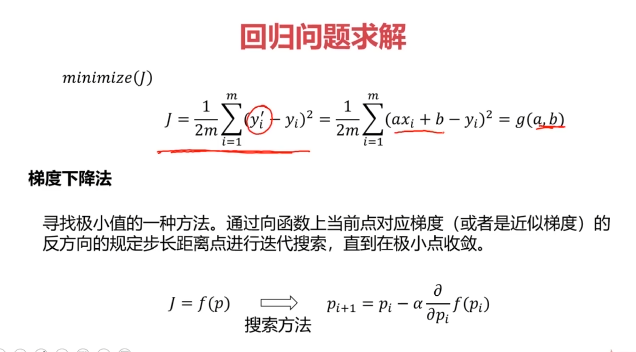
三、线性回归
什么是回归分析?(Regression Analysis)
回归分析
回归分析:根据数据确定两种或两种以上变量间相互依赖的定量关系
函数表达式:
y =f(x1,x2… xn)
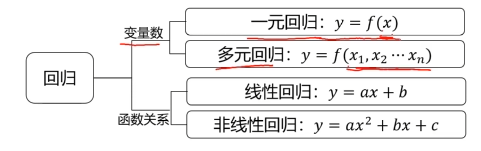
线性回归
线性回归:回归分析中,变量与因变量存在线性关系

Scikit-learn
Python语言中专门针对机器学习应用而发展起来的一款开源框架(算法库),可以实现数据预处理、分类、回归、降维、模型选择等常用的机器学习算法
Scikit-learn特点:
- 集成了机器学习中各类成熟的算法,容易安装和使用,样例丰富,教程和文档也非常详细
- 不支持Python之外的语言,不支持深度学习和强化学习
Scikit-learn官网:https://scikit-learn.org/stable/index.html
Scikit-learn中文社区:https://scikit-learn.org.cn/

pip install scikit-learn -i https://pypi.tuna.tsinghua.edu.cn/simple/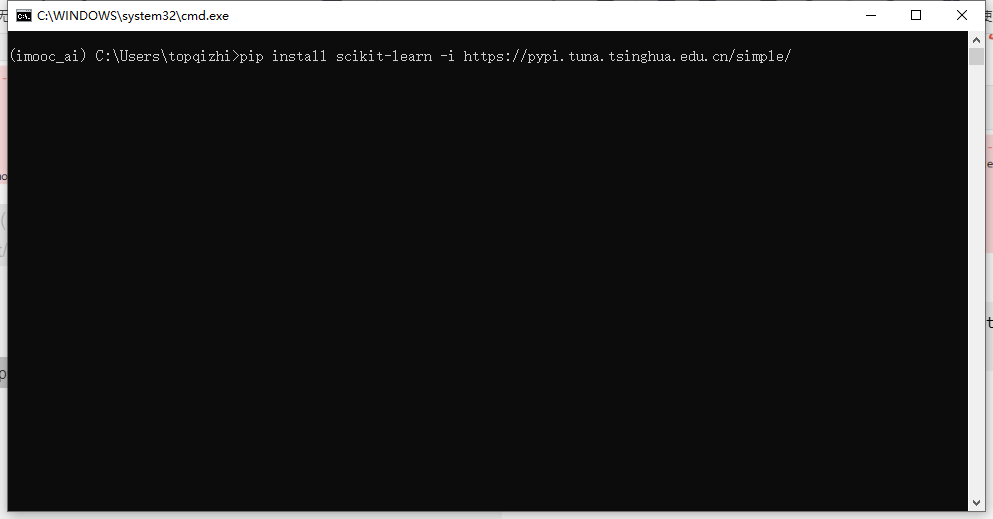
四、单因子线性回归实战
data_single.csv的内容如下:
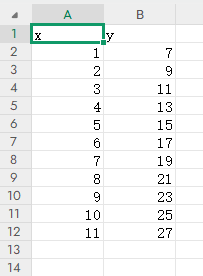
#Python调用Sklearn实现线性回归#数据加载
import pandas as pd
data = pd.read_csv("data_single.csv")
print(type(data),data.shape)
data.head()

#数据赋值
x = data.loc[:,'x']
y = data.loc[:,'y']
print(x,y)
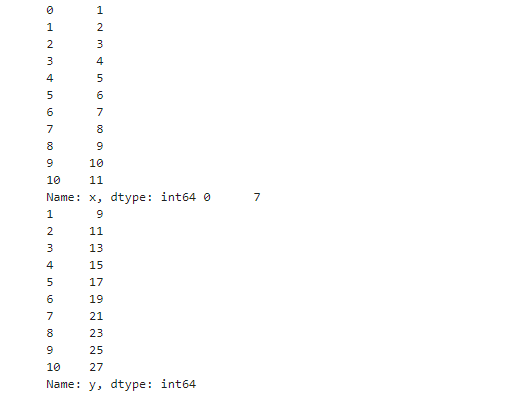
#展示图形
from matplotlib import pyplot as plt
plt.figure(figsize=(3,3))
plt.scatter(x,y)
# plt.show()
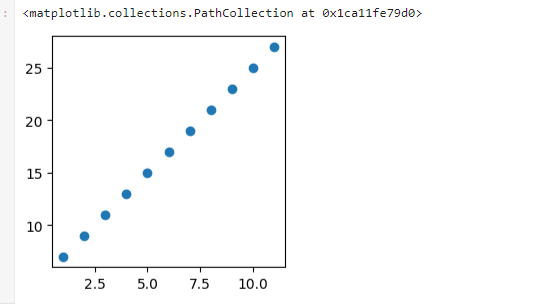
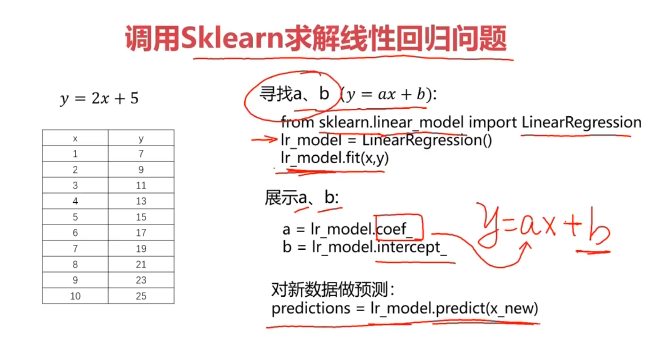
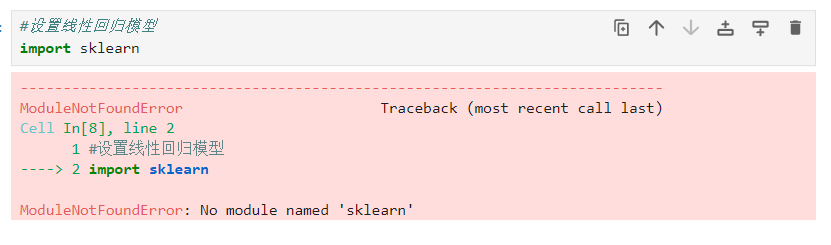
#设置线性回归模型
from sklearn.linear_model import LinearRegression
lr_model = LinearRegression()
#转换维度
import numpy as np
x = np.array(x)
x = x.reshape(-1,1)
print(type(x),x.shape)
y = np.array(y)
y = y.reshape(-1,1)
print(type(y),y.shape)

#训练模型
lr_model.fit(x,y)
#预测x对应的y
y_predict = lr_model.predict(x)
print(y_predict)
print(data)

#使用模型预测x=3.5时y的值
y_3 = lr_model.predict([[3.5]])
print(y_3)

#打印a,b (y = ax + b)
a = lr_model.coef_
b = lr_model.intercept_
print(a,b)

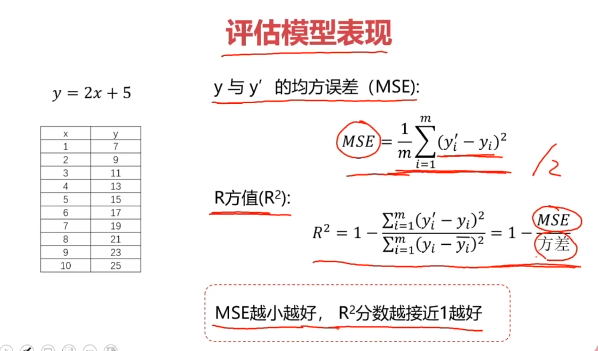
#评估模型的表现
from sklearn.metrics import mean_squared_error,r2_score
MSE = mean_squared_error(y,y_predict)
R2 = r2_score(y,y_predict)
print(MSE,R2)
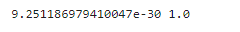
- MSE越小越好,R2分数越接近1越好
- y vs y_predict集中度越高越好(越接近直线分布)
#画图展示 y vs y_predict集中度
plt.figure()
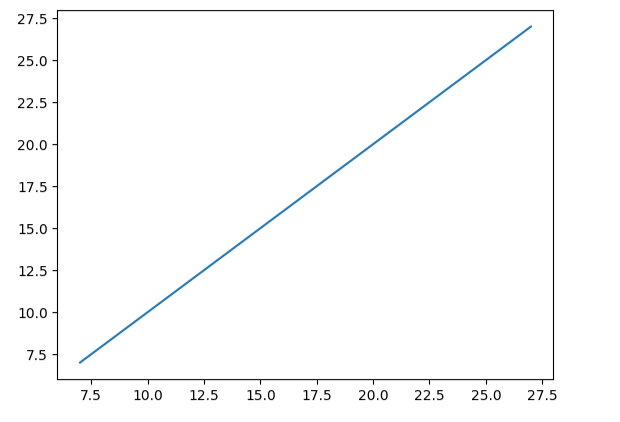
plt.plot(y,y_predict)
plt.show()
四、多因子线性回归实战
预测房价问题,数据集:usa_housing_price.csv
#加载数据
import pandas as pd
import numpy as np
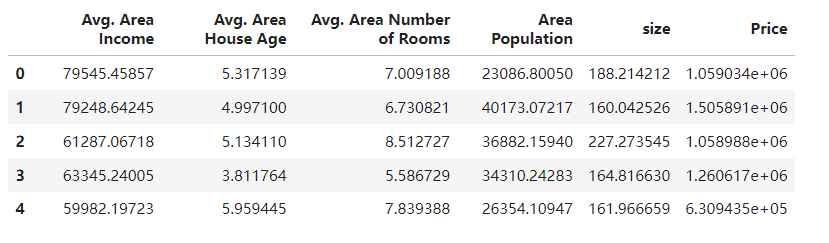
data = pd.read_csv('usa_housing_price.csv')
data.head()
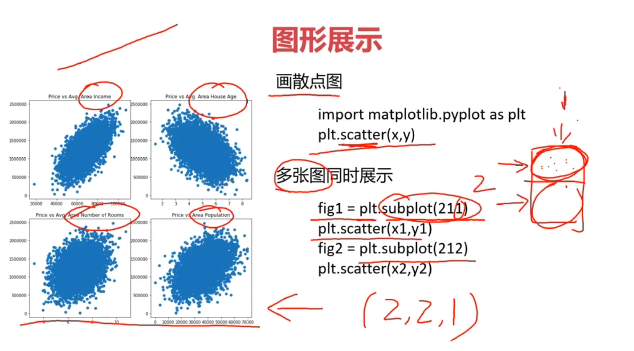
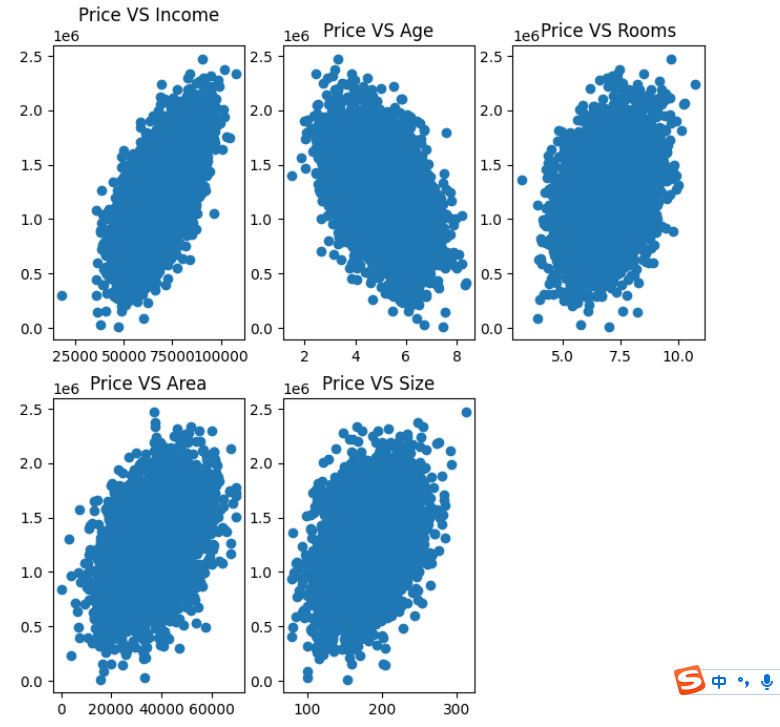
#画图展示(展示在一幅图中,2行3列图)
from matplotlib import pyplot as plt
fig = plt.figure(figsize=(8,8))
fig1 = plt.subplot(231)
plt.scatter(data.loc[:,'Avg. Area Income'],data.loc[:,'Price'])
plt.title('Price VS Income')fig2 = plt.subplot(232)
plt.scatter(data.loc[:,'Avg. Area House Age'],data.loc[:,'Price'])
plt.title('Price VS Age')fig3 = plt.subplot(233)
plt.scatter(data.loc[:,'Avg. Area Number of Rooms'],data.loc[:,'Price'])
plt.title('Price VS Rooms')fig4 = plt.subplot(234)
plt.scatter(data.loc[:,'Area Population'],data.loc[:,'Price'])
plt.title('Price VS Area')fig5 = plt.subplot(235)
plt.scatter(data.loc[:,'size'],data.loc[:,'Price'])
plt.title('Price VS Size')
plt.show()
#定义 x 和 y
x = data.loc[:,'size']
y = data.loc[:,'Price']
x.head()
y.head()
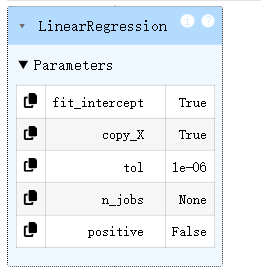
#创建线性回归模型
from sklearn.linear_model import LinearRegression
LR1 = LinearRegression()
#数组进行维度转换
x = np.array(x).reshape(-1,1)
print(x.shape)

#训练模型
LR1.fit(x,y)
#计算单因子对应的价格
y_predict_1 = LR1.predict(x)
print(y_predict_1)
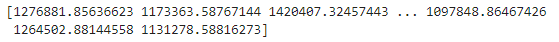
#评估预测模型
from sklearn.metrics import mean_squared_error,r2_score
mean_squared_error_1 = mean_squared_error(y,y_predict_1)
r2_score_1 = r2_score(y,y_predict_1)
print(mean_squared_error_1,r2_score_1)
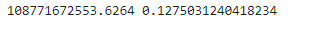
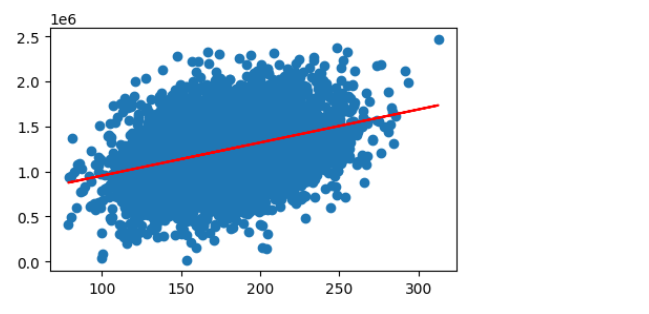
#可视化预测结果
fig6 = plt.figure(figsize=(5,3))
plt.scatter(x,y)
plt.plot(x,y_predict_1,'r')
plt.show()
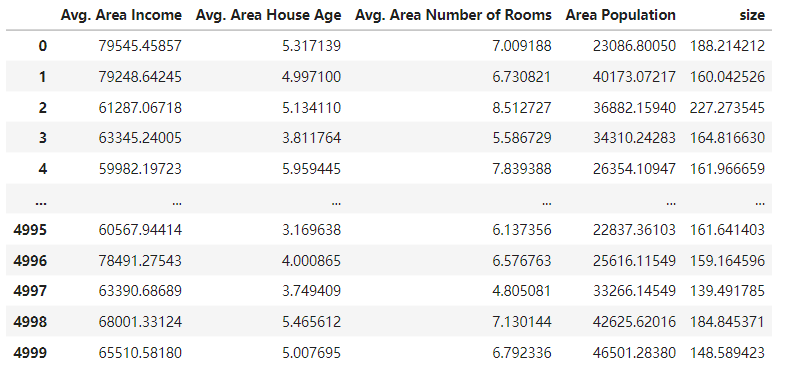
#多因子
x_multi = data.drop(['Price'],axis=1)
x_multi
#创建多因子回归模型
LR_multi = LinearRegression()
#训练模型
LR_multi.fit(x_multi,y)
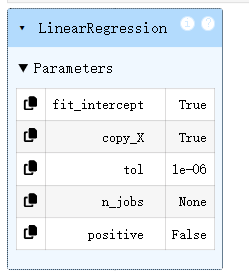
#模型的预测
y_predict_multi = LR_multi.predict(x_multi)
print(y_predict_multi)

#评估预测模型
mean_squared_error_multi = mean_squared_error(y,y_predict_multi)
r2_score_multi = r2_score(y,y_predict_multi)
print(mean_squared_error_1,r2_score_1)
print(mean_squared_error_multi,r2_score_multi)

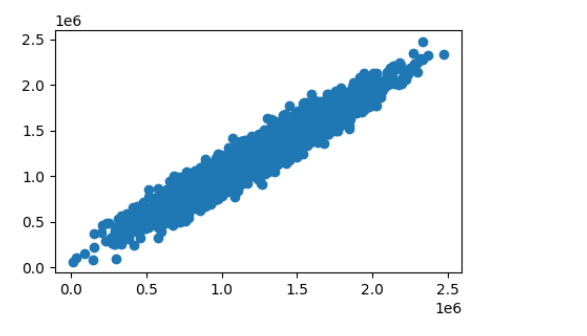
#多因子y,y_predict_multi对比
fig7 = plt.figure(figsize=(5,3))
plt.scatter(y,y_predict_multi)
plt.show()
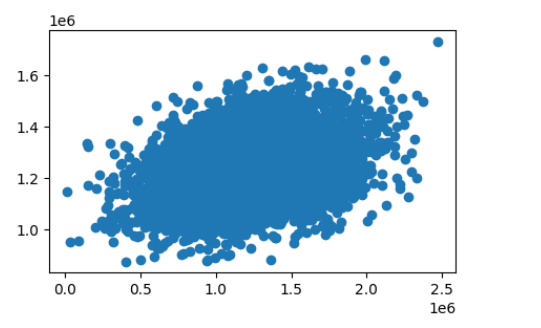
#单因子y,y_predict_1对比
fig8 = plt.figure(figsize=(5,3))
plt.scatter(y,y_predict_1)
plt.show()
#测试多因子模型效果
X_test = [65000,5,5,30000,200]
# X_test = np.array(X_test).reshape(1,-1)X_test = pd.DataFrame(np.array(X_test).reshape(1,-1),columns=['Avg. Area Income','Avg. Area House Age','Avg. Area Number of Rooms','Area Population','size',])
print(X_test)
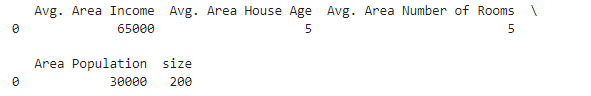
#预测房价
y_test_predict = LR_multi.predict(X_test)
print(y_test_predict)


