Mip-splatting
论文名称:Mip-Splatting: Alias-free 3D Gaussian Splatting
作者:Zehao Yu Anpei Chen Binbin Huang Torsten Sattler Andreas Geiger
论文地址:arxiv.org/pdf/2311.16493
Motivation:
经典3DGS训练的时候会学出来许多很薄的高斯,但在屏幕空间里再用2D dilation把能量铺开,在训练分辨率下看不到问题;但是一旦改变采样率就会出现 zoom-in、zoom-out、高频振铃等伪影。作者把这个问题归结到了:
没有3D频率约束+2D dilation不符合物理积分
3D频率约束:
针孔模型里面,在相机深度为d的位置,一个像素对应的世界尺度大概是T=d/f(f是相机焦距)。
所以相机只能可靠的看到与
成正比的世界频率
对于单个的Gaussian 不管是做傅里叶变换还是高斯,越窄(Σ的特征值越小)就代表频谱越宽。更精确地说:
沿着某个特征向量e的空间标准差时 (λ是该方向的特征值),这个方向上的有效带宽大致与
成正比
-
所以对于针一样的Gaussian:空间域很尖-->频域极宽,包含一堆超过
的高频
-
而对于片状或者薄壳结构:在较薄的法向上也是同理的,也会带来超带宽
经典的3DGS的训练目标是图像域的重建损失(MSE/LPIPS等),没有对3D模型在世界域的频率进行限制,
不论是在边缘处不断地 densification&split 还是 把相近的Gaussian染上交错的颜色,都会导致超带宽的发生
所以标准的3DGS训练会导致学出比T还要精细的结构,结果就是:
在训练视角下,看可能起来还行
但缩放分辨率后,超出采样带宽的细节就会以亮度漂移、锯齿、闪烁的方式表现出来
2D dilation不符合物理积分:
理想的针孔成像模型中,一个像素p的读数不是在像素中心取样,而是对其面积进行积分:
是p的足迹
由采样定理得知的是,当一个连续信号离散化时,如果直接在中心点取样,就会把超过带宽的高频混叠到低频,就会表现出相应的锯齿、闪烁、亮度漂移。
而在传统的3DGS中,是直接进行了dilation,也就是
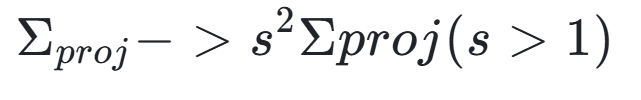
也就是人工将屏幕核放大。但这不是面积积分
Methods:
对于3D频率问题
做法是给每一3D高斯与一个各向同性的3D低通高斯做卷积。两个高斯经过卷积仍然是高斯,等价于给协方差加上一个各项同性项,并用一个行列式比值做能量归一。
具体来说:
先寻找最大采样率,对于第k个高斯中心 ,在训练集的N个相机里取可见视角的v的最大值为
之后进行低通卷积
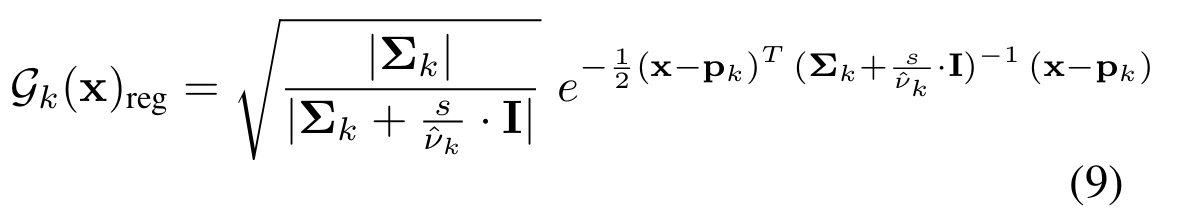
这样虽然协方差变“胖”,但是前面的行列式比值项保证了整体能量的守恒
这个卷积是怎么做的?
可以从一维进行拓展到高维,实际结果是均值相加,方差/协方差相加
简单的做法是推导高斯的特征函数,在相应的协方差矩阵后加上A(Σ的分解上三角矩阵)
令X=μ+AU U服从I的正态分布,之后进行简单的指数运算就可以得到
在高维下,结果依然成立
对于2D dilation 问题
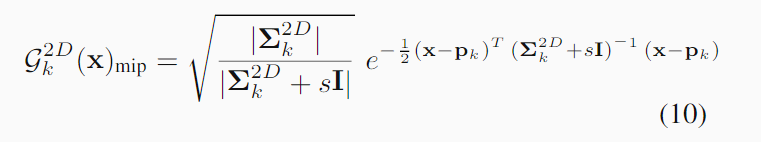
其中s的单位是$pixel^2 I是2*2单位阵
其实整体思路是一致的,前面的行列式比值项同样是为了保证能量守恒
后面是使用一个同位置的标准差为0.3~0.5的各向同性高斯(近似1px的盒滤)与投影到屏幕上的2D Gaussain做卷积运算,来近似真实的像素面积积分,这样达到更精准的目的
Train
Train上简单的来说也就只是将传统的2D dilation更换为像素足迹积分,并周期性的进行3D频率限制
Result
就是通过这样简单的操作,却取得了优秀的效果
