当前位置：首页 > ai >正文

机器学习（二）特征工程

ai 2025/8/27 13:12:59

一、概率

特征工程就是对特征进行相关的处理。就是将任意数据，如文本或图像，转换为可用于机器学习的数字特征，比如字典特征提取也就是特征离散化、文本特征提取、图像特征提取。

一般使用pandas来进行数据清洗和数据处理、使用sklearn进行特征工程。

二、步骤

1、特征提取

不是像dataframe那样的数据，就要进行特征提取，例如文本特征提取、图像特征提取。

2、无量纲化，也就是预处理

归一化、标准化

3、降维

底方差过滤特征选择；主成分分析-PCA降维。

三、特征工程API

转换器类：

DictVectorizer     字典特征提取
CountVectorizer    文本特征提取
TfidfVectorizer    TF-IDF文本特征词的重要程度特征提取
MinMaxScaler        归一化
StandardScaler        标准化
VarianceThreshold    底方差过滤降维
PCA                 主成分分析降维

转换器对象调用fit_transform()进行转换, 其中fit用于计算数据，transform进行最终转换；

fit_transform()可以使用fit()和transform()代替。

data_new = transfer.fit_transform(data)
#可写成
transfer.fit(data)
data_new = transfer.transform(data)

1 DictVectorizer 字典列表特征提取

稀疏矩阵是指一个矩阵中大部分元素为零，只有少数元素是非零的矩阵。

由于稀疏矩阵中零元素非常多，存储和处理稀疏矩阵时，通常会采用特殊的存储格式，以节省内存空间并提高计算效率。

三元组表就是一种稀疏矩阵类型数据,存储非零元素的行索引、列索引和值:

(行,列) 数据
(0,0) 10
(0,1) 20
(2,0) 90
(2,20) 8
(8,0) 70

表示除了列出的有值, 其余全是0

非稀疏矩阵（稠密矩阵）是指矩阵中非零元素的数量与总元素数量相比接近或相等。

在这种情况下，矩阵的存储通常采用标准的二维数组形式，因为非零元素密集分布，不需要特殊的压缩或优化存储策略。

两者比较：

存储：稀疏矩阵使用特定的存储格式来节省空间，而稠密矩阵使用常规的数组存储所有元素，无论其是否为零。

计算：稀疏矩阵在进行计算时可以利用零元素的特性跳过不必要的计算，从而提高效率。而稠密矩阵在计算时需要处理所有元素，包括零元素。

应用领域：稀疏矩阵常见于大规模数据分析、图形学、自然语言处理、机器学习等领域，而稠密矩阵在数学计算、线性代数等通用计算领域更为常见。

1.1 API

sklearn.feature_extraction.DictVectorizer(sparse=True)

参数:

sparse=True返回类型为csr_matrix的稀疏矩阵

sparse=False表示返回的是数组,数组可以调用.toarray()方法将稀疏矩阵转换为数组

转换器对象调用fit_transform(data)函数，参数data为一维字典数组或一维字典列表,返回转化后的矩阵或数组；转换器对象get_feature_names_out()方法获取特征名。

from sklearn.feature_extraction import DictVectorizer
import pandas
data = [{'city':'成都', 'age':30, 'temperature':200}, {'city':'重庆','age':33, 'temperature':60}, {'city':'北京', 'age':42, 'temperature':80}]
#创建DictVectorizer对象
transfer = DictVectorizer(sparse=False)#sparse=True，就是可以输出稀疏矩阵
#转换器对象调用这个函数进行转换，fit用于计算数据，transform用于最终转换
data_new = transfer.fit_transform(data)
# data_new的类型为ndarray
#特征数据
print("data_new:\n", data_new)
#特征名字 
print("特征名字：\n", transfer.get_feature_names_out())
#提取稀疏矩阵对应的数组
pandas.DataFrame(data_new, columns=transfer.get_feature_names_out())

结果：
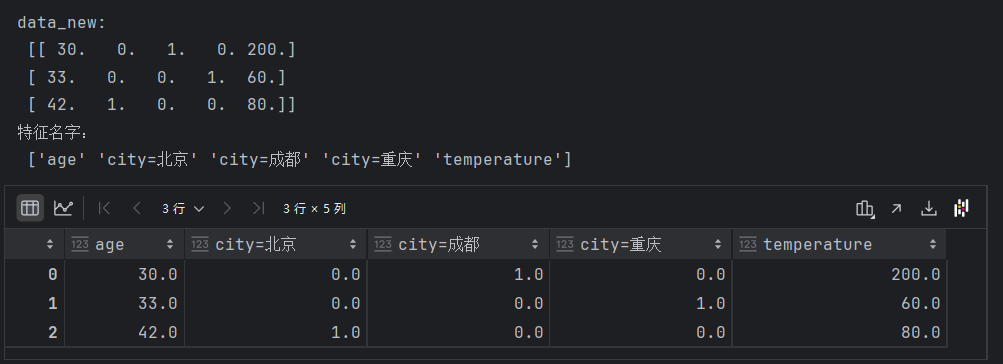稀疏矩阵对象调用toarray()函数，得到类型为ndarray的二维稀疏矩阵。

2 CountVectorizer 文本特征提取

1.1 API

sklearn.feature_extraction.text.CountVectorizer

构造函数关键字参数stop_words，值为list，表示词的黑名单(不提取的词)，fit_transform函数的返回值为稀疏矩阵。

1.2 英文文本提取

from sklearn.feature_extraction.text import CountVectorizer
import pandas
data=["stu is well, stu is great", "You like stu"]
#创建转换器对象, you和is不提取
transfer = CountVectorizer(stop_words=["you","is"])#进行提取,得到稀疏矩阵
data_new = transfer.fit_transform(data)
print(data_new)pandas.DataFrame(data_new.toarray(), index=["第一个句子","第二个句子"],columns=transfer.get_feature_names_out())

结果：

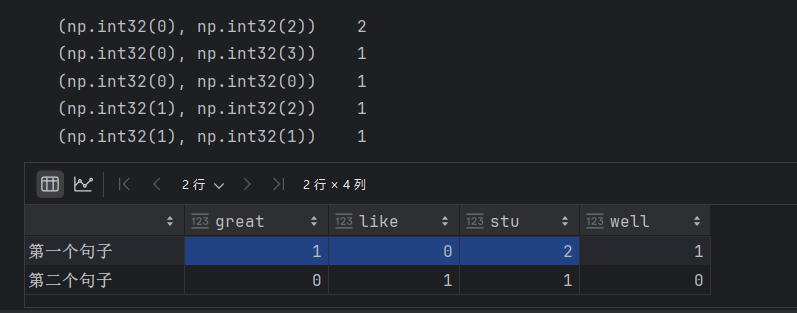
1.3 中文文本提取

中文文本文字之间没有空格，所以要先分词，一般使用jieba分词。

import jieba
import pandas as pd
from sklearn.feature_extraction.text import CountVectorizer
'''使用jieba封装一个函数，就是把汉语字符串中进行分词。'''
def cut(text):return " ".join(list(jieba.cut(text)))data = ["教育学会会长期间坚定支持民办教育事业！","热忱关心、扶持民办学校发展","事业做出重大贡献！"]
data_new = [cut(v) for v in data]
#创建转换器对象
transfer = CountVectorizer(stop_words=['期间', '做出']) 
#转换器对象调用这个函数进行转换，fit用于计算数据，transform用于最终转换
data_final = transfer.fit_transform(data_new)print(data_final.toarray())#把非稀疏矩阵转变为稀疏矩阵
print(transfer.get_feature_names_out())#特征名称
#提取稀疏矩阵对应的数组
pd.DataFrame(data_final.toarray(), columns=transfer.get_feature_names_out())

结果：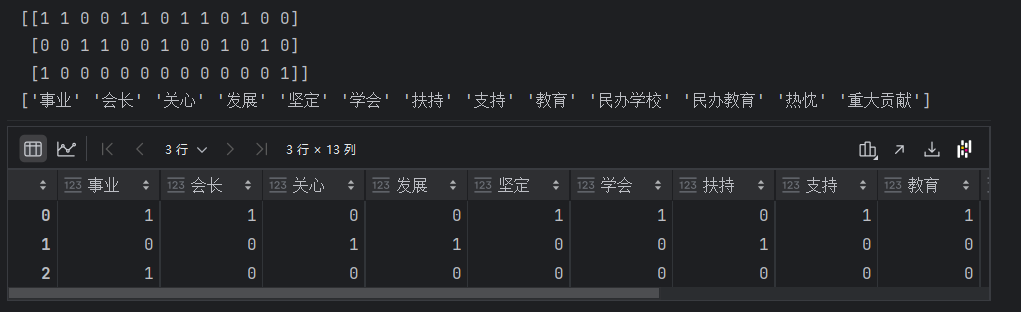

3TfidfVectorizer TF-IDF文本特征词的重要程度特征提取

TF(词频）：某个词在文章中出现的次数/文章总次数；

词频是指一个词在文档中出现的频率。

原始词频：一个词在文档中出现的次数除以文档中总的词数。
平滑后的词频：为了防止高频词主导向量空间，有时会对词频进行平滑处理，例如使用 1 + log(TF)。
在 TfidfVectorizer 中，TF 默认是：直接使用一个词在文档中出现的次数也就是CountVectorizer的结果

IDF(逆文档频率）:lg(语料库的文档总数/包含该词的文档数+1);

但在TfidfVectorizer 中，IDF 的默认计算公式需要在后面+1。

逆文档频率衡量一个词的普遍重要性。如果一个词在许多文档中都出现，那么它的重要性就会降低。

在 TfidfVectorizer 中还会进行归一化处理(采用的L2归一化)

1.1 API

sklearn.feature_extraction.text.TfidfVectorizer()

构造函数关键字参数stop_words，表示词特征黑名单;fit_transform函数的返回值为稀疏矩阵。

1.2 代码示例

import jieba
import pandas as pd
from sklearn.feature_extraction.text import TfidfVectorizerdef cut_words(text):return " ".join(list(jieba.cut(text)))data = ["教育学会会长期间，坚定支持民办教育事业！",  "扶持民办,学校发展事业","事业做出重大贡献！"]
data_new = [cut_words(v) for v in data]
#只在这里修改成为TfidfVectorizer
transfer = TfidfVectorizer(stop_words=['期间', '做出',"重大贡献"]) 
data_final = transfer.fit_transform(data_new)pd.DataFrame(data_final.toarray(), columns=transfer.get_feature_names_out())

结果：

四、无量纲化-预处理

无量纲就是没有单位的数据。

1 MinMaxScaler归一化

通过对原始数据进行变化把数据映射到指定区间，默认为0-1。

1.1 公式

$Xscaled=\frac{X-Xmin}{Xmax-Xmin}$

𝑥min 和 𝑥max 分别是每种特征中的最小值和最大值，而 𝑥是当前特征值，𝑥scaled 是归一化后的特征值。

1.2 API

sklearn.preprocessing.MinMaxScaler(feature_range)

参数:feature_range=(0,1) 归一化后的值域,可以自己设定；fit_transform函数归一化的原始数据类型可以是list、DataFrame和ndarray, 不可以是稀疏矩阵；fit_transform函数的返回值为ndarray。

1.3代码实例

from sklearn.preprocessing import MinMaxScaler
data=[[12,22,4],[22,23,1],[11,23,9]]
#feature_range=(0, 1)表示归一化后的值域,可以自己设定
transfer = MinMaxScaler(feature_range=(0, 1))
#data_new的类型为<class 'numpy.ndarray'>
data_new = transfer.fit_transform(data)
print(data_new)

结果：
[[0.09090909 0. 0.375 ]
[1. 1. 0. ]
[0. 1. 1. ]]

1.4 缺点

最大值和最小值最容易收到异常点影响，所以鲁棒性较差。

我们一般使用标准化的无量纲化。

2 normalize归一化

2.1 L1归一化

绝对值相加为分母，特征值为分子；

2.2 L2归一化

平方相加作为分母，特征值作为分子。

2.3 max归一化

max值为分母，特征值为分子。

from sklearn.preprocessing import normalize
normalize(data, norm='l2', axis=1)
"""data是要归一化的数据,norm是使用那种归一化:l1\l2\max,axis=0是列  axis=1是行"""

3 StandardScaler标准化

标准化是一种数据预处理技术，也称为数据归一化或特征缩放。是将不同特征的数值范围缩放到统一的标准范围，特别是那些对输入数据的尺度敏感的算法。

3.1 标准化公式

Z-score标准化，也称为零均值标准化。它通过对每个特征的值减去其均值，再除以其标准差，将数据转换为均值为0，标准差为1的分布。

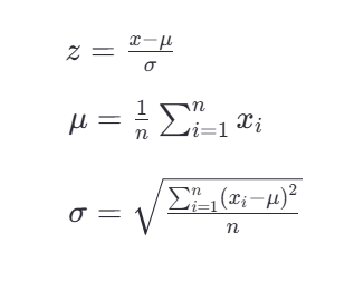
z是转换后的数值，x是原始数据值，u是该特征的均值， $\sigma$ 是该特征的标准差。

1.1 API

sklearn.preprocessing.StandardScale

与MinMaxScaler一样，原始数据类型可以是list、DataFrame和ndarray，fit_transform函数的返回值为ndarray, 归一化后得到的数据类型都是ndarray。

import pandas as pd
import numpy as np
from sklearn.preprocessing import StandardScaler
# 1、获取数据
df_data = pd.read_csv("src/dating.txt")
print(type(df_data)) #<class 'pandas.core.frame.DataFrame'>
print(df_data.shape) #(1000, 4)# 2、实例化一个转换器类
transfer = StandardScaler()# 3、调用fit_transform#把DateFrame数据进行归一化
new_data = transfer.fit_transform(df_data)
print("DateFrame数据被归一化后:\n", new_data[0:5])#把DateFrame转为ndarray
nd_data = df_data.values#把ndarray数据进行归一化
new_data = transfer.fit_transform(nd_data)
print("ndarray数据被归一化后:\n", new_data[0:5])#把DateFrame转为list
nd_data = df_data.values.tolist()#把ndarray数据进行归一化
new_data = transfer.fit_transform(nd_data)
print("list数据被归一化后:\n", new_data[0:5])

结果：
<class 'pandas.core.frame.DataFrame'>
(1000, 4)
DateFrame数据被归一化后:
[[ 0.33193158 0.41660188 0.24523407 1.24115502]
[-0.87247784 0.13992897 1.69385734 0.01834219]
[-0.34554872 -1.20667094 -0.05422437 -1.20447063]
[ 1.89102937 1.55309196 -0.81110001 -1.20447063]
[ 0.2145527 -1.15293589 -1.40400471 -1.20447063]]
ndarray数据被归一化后:
[[ 0.33193158 0.41660188 0.24523407 1.24115502]
[-0.87247784 0.13992897 1.69385734 0.01834219]
[-0.34554872 -1.20667094 -0.05422437 -1.20447063]
[ 1.89102937 1.55309196 -0.81110001 -1.20447063]
[ 0.2145527 -1.15293589 -1.40400471 -1.20447063]]
list数据被归一化后:
[[ 0.33193158 0.41660188 0.24523407 1.24115502]
[-0.87247784 0.13992897 1.69385734 0.01834219]
[-0.34554872 -1.20667094 -0.05422437 -1.20447063]
[ 1.89102937 1.55309196 -0.81110001 -1.20447063]
[ 0.2145527 -1.15293589 -1.40400471 -1.20447063]]

不使用API的实现过程：

#数据
data=np.array([[5],[20],[40],[80],[100]])
#API实现标准化
data_news=scaler.fit_transform(data)
print("API实现:\n",data_news)#标准化自己实现
mu=np.mean(data)
sum=0
for i in data:sum+=((i[0]-mu)**2)
d=np.sqrt(sum/(len(data)))
print("自己实现:\n",(data[3]-mu)/d)

1.2 注意点

在数据预处理中，fit、fit_transform和transform这三个方法各自有不同的作用。

fit:用来计算数据的统计信息，比如均值和标准差（在StandardScaler的情况下）。这些统计信息随后会被用于数据的标准化，应当仅在训练集上使用fit方法。

fit_transform:先调用fit再调用transform，但内部执行得更高效。仅在训练集上使用，计算训练集的统计信息并立即应用到该训练集上。

transform通过fit方法计算出的统计信息来转换数据。应用于任何数据集，包括训练集、验证集或测试集，但是应用时使用的统计信息必须来自于训练集。

在预处理数据时，首先在训练集X_train上使用fit_transform，一次性完成统计信息的计算和数据的标准化。

一旦scaler对象在X_train上被fit，它就已经知道了如何将数据标准化。

这时测试集X_test只需要使用transform方法，因为不希望在测试集上重新计算任何统计信息，也不希望测试集的信息影响到训练过程。如果我们对X_test也使用fit_transform，测试集的信息就可能会影响到训练过程。

总结:先fit_transform(x_train),然后再transform(x_text)。

五、特征降维

降维就是去掉一些特征,或者转化多个特征为少量个特征，减少数据集的维度，同时尽可能保留数据的重要信息。

1 特征降维的好处

减少计算成本：在高维空间中处理数据可能非常耗时且计算密集。降维可以简化模型，降低训练时间和资源需求。

去除噪声：高维数据可能包含许多无关或冗余特征，可能引入噪声并导致过拟合。降维可以帮助去除这些不必要的特征。

2 特征降维的方式

特征选择
- 从原始特征集中挑选出最相关的特征
主成份分析(PCA)
- 主成分分析就是把之前的特征通过一系列数学计算，形成新的特征，新的特征数量会小于之前特征数量

3 特征选择

3.1 VarianceThreshold 低方差过滤特征选择

Filter(过滤式): 主要探究特征本身特点，特征与特征、特征与目标值之间关联

低方差特征过滤，如果一个特征的方差很小，这个特征的值在样本中几乎相同或变化不大，包含的信息量很少，模型很难通过该特征区分不同的对象。

1、计算方差：对于每个特征，计算其在训练集中的方差(每个样本值与均值之差的平方,在求平均)。

2、设定阈值：选择一个方差阈值，任何低于这个阈值的特征都将被视为低方差特征。

3、过滤特征：移除所有方差低于设定阈值的特征。

from sklearn.feature_selection import VarianceThreshold
import pandas as pd
def variance_demo():# 1、获取数据,data是一个DataFrame,可以是读取的csv文件data=pd.DataFrame([[10,1],[11,3],[11,1],[11,5],[11,9],[11,3],[11,2],[11,6]])print("data:\n", data)   # 2、实例化一个转换器类'''创建对象，方差为小于等于0.1的去掉，threshold的缺省值为0.1'''transfer = VarianceThreshold(threshold=1)# 3、调用fit_transform"""把data_new中低方差特征去掉，类型可以是DataFrame、ndarray和list"""data_new = transfer.fit_transform(data)print("data_new:\n",data_new)return None
variance_demo()

结果：

data:
0 1
0 10 1
1 11 3
2 11 1
3 11 5
4 11 9
5 11 3
6 11 2
7 11 6
data_new:
[[1]
[3]
[1]
[5]
[9]
[3]
[2]
[6]]

3.2 根据相关系数的特征选择

3.2.1 相关性

在正相关的关系中，两个变量的变化趋势是同向的。

当两个变量正相关时，意味着：如果第一个变量增加，第二个变量也有很大的概率会增加；同样，如果第一个变量减少，第二个变量也很可能会减少。

正相关性并不意味着一个变量的变化直接引起了另一个变量的变化，仅指出了两个变量之间存在的一种统计上的关联性。这种关联性可以是因果关系，也可以是由第三个未观察到的变量引起的，或者是纯属巧合。

正相关性通常用正值的相关系数来表示，值介于0和1之间。当相关系数等于1时，表示两个变量之间存在完美的正相关关系，即一个变量的值可以完全由另一个变量的值预测。

负相关性与正相关性刚好相反,不相关指两者的相关性很小,一个变量变化不会引起另外的变量变化,只是没有线性关系。

3.2.2 皮尔逊相关系数

一种度量两个变量之间线性相关性的统计量。它提供了两个变量间关系的方：正相关、负相关，还有和强度的信息。

皮尔逊相关系数的取值范围是 [−1,1]，相关系数 $\rho$ 的绝对值为0-1之间，绝对值越大，表示越相关，其中：

$\rho$ =1 表示完全正相关，即随着一个变量的增加，另一个变量也线性增加。
$\rho$ =-1 表示完全负相关，即随着一个变量的增加，另一个变量线性减少。
$\rho$ =0 表示两个变量之间不存在线性关系。

当两特征完全相关时，两特征的值表示的向量是在同一条直线上，当两特征的相关系数绝对值很小时，两特征值表示的向量接近在同一条直线上。当相关系值为负数时，表示负相关

pearsonr相关系数计算公式, 该公式出自于概率论，对于两组数据 𝑋={𝑥1,𝑥2,...,𝑥𝑛} 和 𝑌={𝑦1,𝑦2,...,𝑦𝑛}，皮尔逊相关系数可以用以下公式计算：

$\rho=\frac{\operatorname{Cos}(x, y)}{\sqrt{D x} \cdot \sqrt{D y}}=\frac{E[(x_-E x)(y-E y)]}{\sqrt{D x} \cdot \sqrt{D y}}=\frac{\sum_{i=1}^{n}(x-\tilde{x})(y-\bar{y}) /(n-1)}{\sqrt{\sum_{i=1}^{n}(x-\bar{x})^{2} /(n-1)} \cdot \sqrt{\sum_{i=1}^{n}(y-\bar{y})^{2} /(n-1)}}$

$\bar{x}$ 和 $\bar{y}$ 分别是𝑋和𝑌的平均值。

|ρ|<0.4为低度相关; 0.4<=|ρ|<0.7为显著相关； 0.7<=|ρ|<1为高度相关；

API

计算两特征之间的相关性

scipy.stats.personr(x, y)

返回对象有两个属性:

statistic皮尔逊相关系数[-1,1]

pvalue零假设(了解),统计上评估两个变量之间的相关性,越小越相关

variance_demo()
#%%
from scipy.stats import pearsonr
import numpy as np
# 1、获取数据
data1=[12,22,4,22,23,1,11,23,9]
data2=[8,20,4,20,26,8,12,66,9]
# 计算某两个变量之间的相关系数
r1 = pearsonr(np.array(data1), np.array(data2))
print(r1.statistic) #相关性, 负数表示负相关,正数表示正相关
print(r1.pvalue) #相关性,越小越相关
r2 = pearsonr(data1, data2)
print(r2.statistic)

结果：

0.6776362669868862
0.04489418667952034
0.6776362669868862

tips：但是我们开发一般不使用求相关系数的方法，由于主成分分析过程中包含相关系数，一般使用主成分分析。

4 主成分分析

从原始特征空间中找到一个新的坐标系统，使得数据在新坐标轴上的投影能够最大程度地保留数据的方差，同时减少数据的维度。

使用两个维度表示(x0,y0),将数据映射到红色线上，用线性变换的方式。

从信息损失来看，a不是越大越好或者越小越好，二当a=β时损失最小。

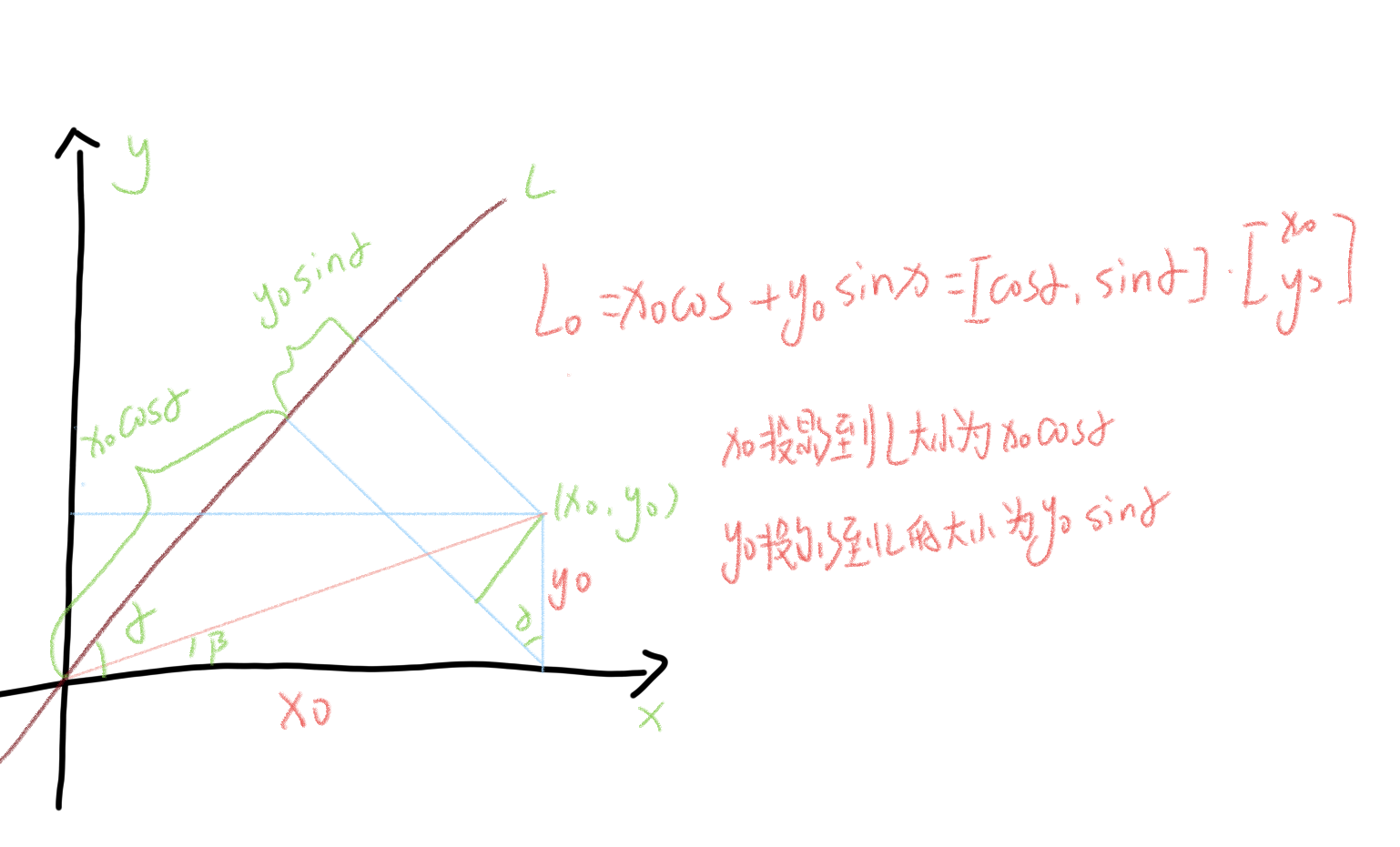
使用(x_0,y_0)表示一个点，表明该点有两个特征，而映射到L上有一个特征就可以表示这个点了。

投影到L上的值就是降维后保留的信息，投影到与L垂直的轴上的值就是丢失的信息。保留信息/原始信息=信息保留的比例。

我们需要找到数据最重要的方式，也就是方差最大的方向。

4.1 步骤

得到矩阵；

用矩阵P对原始数据进行线性变换，得到新的数据矩阵Z,每一列就是一个主成分, 如下图就是把10维降成了2维,得到了两个主成分；

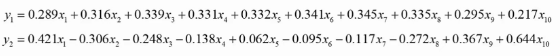
根据主成分的方差，确定最终保留的主成分个数， 方差大的要留下。一个特征的多个样本的值如果都相同，则方差为0，则说明该特征值不能区别样本，所以该特征没有用。

4.2 API

from sklearn.decomposition import PCAPCA(n_components=None)

实参为小数时：表示降维后保留百分之多少的信息

实参为整数时：表示减少到多少特征主成分分析n_components:

1、实参为小数

from sklearn.decomposition import PCA
data = [[2,8,4,5], [6,3,0,8], [5,4,9,1]]
'''1、实例化一个转换器类， 降维后还要保留原始数据0.95%的信息,最后的结果中发现由4个特征降维成2个特征了'''
transfer = PCA(n_components=0.95)'''2、调用fit_transform'''
data_new = transfer.fit_transform(data)
print("data_new:\n", data_new)

结果：
data_new:
[[-1.28620952e-15 3.82970843e+00]
[-5.74456265e+00 -1.91485422e+00]
[ 5.74456265e+00 -1.91485422e+00]]

2、实参为整数

from sklearn.decomposition import PCA
data = [[2,8,4,5], [6,3,0,8], [5,4,9,1]]
'''1、实例化一个转换器类， 降维到只有3个特征'''
transfer = PCA(n_components=3)'''2、调用fit_transform'''
data_new = transfer.fit_transform(data)
print("data_new:\n", data_new)

结果：
data_new:
[[-1.28620952e-15 3.82970843e+00 5.26052119e-16]
[-5.74456265e+00 -1.91485422e+00 5.26052119e-16]
[ 5.74456265e+00 -1.91485422e+00 5.26052119e-16]]

查看全文

http://www.xdnf.cn/news/18760.html