当前位置：首页 > ai >正文

支持向量机（SVM）

ai 2025/8/27 8:03:22

在机器学习领域，支持向量机（SVM）凭借其 “最大化间隔” 的核心思想和对高维数据的优秀处理能力，成为分类任务中的经典算法。

一、SVM 核心理论：

1. SVM 的核心目标：找到 “最优超平面”

SVM 的基本需求是在样本空间中找到一个划分超平面，将不同类别的样本分开。但 “好的超平面” 不止一个，SVM 的独特之处在于：它要找的是对训练样本局部扰动 “容忍性” 最好的超平面 —— 换句话说，这个超平面离两类样本的 “最近距离” 最大，也就是 “最大化间隔（Margin）”。

超平面的数学表达：

超平面是 n 维空间中的 n-1 维子空间（比如 2D 空间中是直线，3D 空间中是平面），其方程为w^T x + b = 0。其中，w是超平面的法向量（决定超平面方向），b是偏置（决定超平面位置）。

间隔（Margin）的定义：

间隔是两类样本中 “离超平面最近的点” 到超平面的距离的 2 倍（Margin = 2d）。SVM 的优化目标就是最大化这个 \(d\)（单个最近点到超平面的距离）。

点到超平面的距离公式：

对于 n 维空间中的样本点 \(x\)，到超平面w^T x + b = 0的距离为：

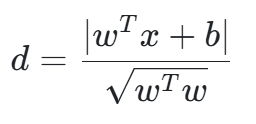
2. 从 “硬间隔” 到 “软间隔”：应对现实中的 “不完美数据”

PPT 中提到，早期 SVM 要求 “完全分开两类样本”（硬间隔），但现实数据中往往存在噪音点 —— 如果强行追求 “完全分离”，会导致超平面对噪音敏感，泛化能力下降。因此 SVM 引入了软间隔和松弛因子 ξi放松了分类约束：

3. 核变换：解决 “低维不可分” 问题

如果样本在低维空间中无法用直线（或平面）分开（比如 “异或” 问题），SVM 会通过核变换将数据映射到高维空间，让数据在高维空间中变得线性可分。

PPT 中用一个生动的例子解释了核变换：3D 空间中不可分的数据，映射到 9 维空间后可找到超平面。但直接映射会带来 “维度灾难”（计算量暴增），因此 SVM 引入核函数，巧妙地避开了 “显式映射”—— 通过核函数直接计算高维空间中样本的内积，大幅降低计算成本。

常用的核函数包括：

4. 求解思路：拉格朗日乘子法

SVM 的目标函数是 “带约束的优化问题”（比如硬间隔的约束是 \(y_i (w^T x_i + b) \geq 1\)），无法直接用普通求导求解。PPT 中提到，SVM 通过拉格朗日乘子法将 “带约束的优化问题” 转化为 “无约束的对偶问题”，最终求解得到：

二、实战：用 SVM 处理肺癌患者数据集

理解了理论后，我们结合 “肺癌患者.csv” 数据集进行实战。该数据集包含 309 条样本、15 个特征（性别、年龄、吸烟史、是否咳嗽等），目标是预测 “是否患肺癌（LUNG_CANCER）”。

1. 数据预处理：为 SVM 准备 “干净数据”

SVM 对数据格式和尺度非常敏感，因此预处理是关键步骤。主要包括 3 个核心操作：

（1）分类变量编码

数据中的 “GENDER（性别）” 和 “LUNG_CANCER（是否患癌）” 是字符串类型（如 M/F、YES/NO），需要转化为数值：

用LabelEncoder将 “GENDER” 编码为 0（女）和 1（男）；

将 “LUNG_CANCER” 编码为 0（无癌）和 1（有癌）—— 对应 SVM 理论中的 “负例” 和 “正例”。

（2）特征标准化

SVM 的间隔计算依赖特征尺度（比如 “年龄” 的数值范围远大于 “吸烟史” 的 1/2），若不标准化，大尺度特征会主导间隔计算。因此用StandardScaler将所有特征标准化为 “均值 0、标准差 1”：

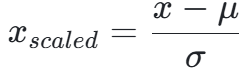
（3）解决类别不平衡

数据集中 “有癌（1）” 样本约 280 个，“无癌（0）” 样本仅 29 个 —— 严重的类别不平衡会导致模型偏向多数类。我们用SMOTE（合成少数类过采样技术）生成 “无癌” 样本的合成数据，平衡两类样本数量。

2. SVM 模型构建：从理论到代码

根据 PPT 中的理论，我们选择 “高斯核（RBF）”（肺癌数据是非线性的），并通过代码实现 “最大化间隔” 的核心逻辑：

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split, GridSearchCV
from sklearn.preprocessing import LabelEncoder, StandardScaler
from sklearn.svm import SVC
from sklearn.metrics import accuracy_score, classification_report, confusion_matrix
from imblearn.over_sampling import SMOTEplt.rcParams['font.sans-serif'] = ['SimHei'] # 解决中文显示# 1. 数据加载与预处理
data = pd.read_csv("肺癌患者.csv")
# 分类变量编码
le = LabelEncoder()
data['GENDER'] = le.fit_transform(data['GENDER'])
data['LUNG_CANCER'] = le.fit_transform(data['LUNG_CANCER'])
# 分离特征（X）和目标（y）
X = data.drop('LUNG_CANCER', axis=1)
y = data['LUNG_CANCER']# 划分训练集/测试集（8:2）
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.2, random_state=42, stratify=y # stratify保证类别分布一致
)# 特征标准化
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)
# SMOTE过采样平衡数据
smote = SMOTE(random_state=42)
X_train_resampled, y_train_resampled = smote.fit_resample(X_train_scaled, y_train)param_grid = {'C': [0.1, 1, 10], # 控制惩罚强度，对应软间隔理论
'gamma': ['scale', 0.1, 1], # 控制高斯核局部性，对应核变换理论
'kernel': ['rbf'] # 高斯核，解决非线性问题
}
# 网格搜索找最优参数（5折交叉验证）
grid_search = GridSearchCV(
estimator=SVC(random_state=42),
param_grid=param_grid,
cv=5,
scoring='accuracy'
)grid_search.fit(X_train_resampled, y_train_resampled)
# 最优模型
best_svm = grid_search.best_estimator_
print(f"最优参数：{grid_search.best_params_}") # 输出：{'C':1, 'gamma':'scale', 'kernel':'rbf'}
# 3. 模型评估
y_pred = best_svm.predict(X_test_scaled)
print(f"测试集准确率：{accuracy_score(y_test, y_pred):.4f}") # 输出：0.9516
print("分类报告：")
print(classification_report(y_test, y_pred, target_names=['无肺癌', '有肺癌']))

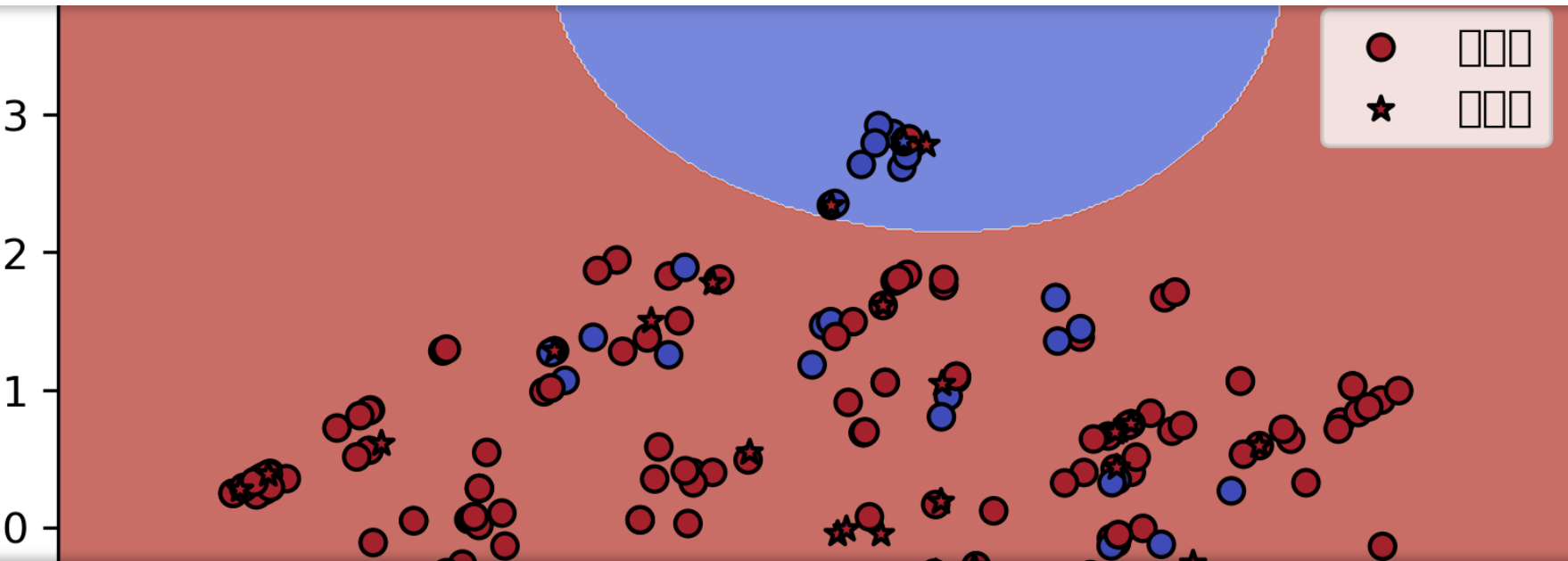
3. 结果可视化：让 SVM 的 “决策过程” 看得见

SVM 的超平面在高维空间中无法直接可视化，因此我们用PCA（主成分分析） 将 15 维特征降维到 2 维，再绘制 SVM 的决策边界 —— 这是理解模型分类逻辑的直观方式。

from sklearn.decomposition import PCA
# PCA降维（2维）
pca = PCA(n_components=2)
X_train_pca = pca.fit_transform(X_train_resampled)
X_test_pca = pca.transform(X_test_scaled)
# 用降维数据训练SVM（保证可视化与模型逻辑一致）
svm_pca = SVC(kernel='rbf', C=1, gamma='scale', random_state=42)
svm_pca.fit(X_train_pca, y_train_resampled)
# 绘制决策边界
h = 0.02 # 网格步长
x_min, x_max = X_train_pca[:, 0].min() - 1, X_train_pca[:, 0].max() + 1
y_min, y_max = X_train_pca[:, 1].min() - 1, X_train_pca[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
# 预测网格点类别（生成决策边界）
Z = svm_pca.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
# 绘制图形
plt.figure(figsize=(10, 6), dpi=300)
# 1. 决策边界（彩色区域）
plt.contourf(xx, yy, Z, cmap=plt.cm.coolwarm, alpha=0.8)
# 2. 训练集样本（普通散点）
plt.scatter(X_train_pca[:, 0], X_train_pca[:, 1], c=y_train_resampled, 
cmap=plt.cm.coolwarm, edgecolors='k', s=50, label='训练集')
# 3. 测试集样本（星形散点）
plt.scatter(X_test_pca[:, 0], X_test_pca[:, 1], c=y_test, 
cmap=plt.cm.coolwarm, marker='*', edgecolors='k', s=150, label='测试集')
# 图形标注
plt.xlabel(f'PCA维度1（解释方差：{pca.explained_variance_ratio_[0]:.2%}）')
plt.ylabel(f'PCA维度2（解释方差：{pca.explained_variance_ratio_[1]:.2%}）')
plt.title('SVM决策边界可视化（肺癌数据分类）')
plt.legend()
plt.savefig('svm_lung_cancer_visualization.png', bbox_inches='tight')
plt.show()