DFS序与树链剖分入门
DFS 序列
定义
DFS 序是指:每个节点在 DFS 深度优先遍历中的进出栈的时间序列。
所以它有什么用呢
我们知道,树是一种非线性的数据结构,它的一些数据调用肯定是没有线性结构来得方便的。所以这个时候,dfs站了出来。基于dfs函数,我们可以在遍历的同时记录下每个节点进出栈的时间序列。比如有这样一颗树:
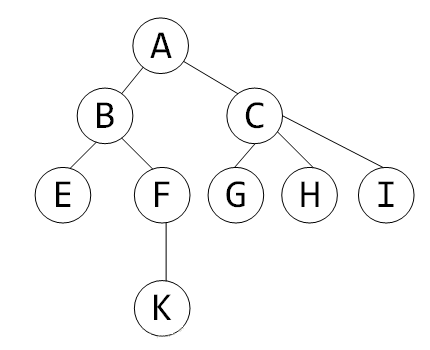
那么它的 DFS 序列就是:
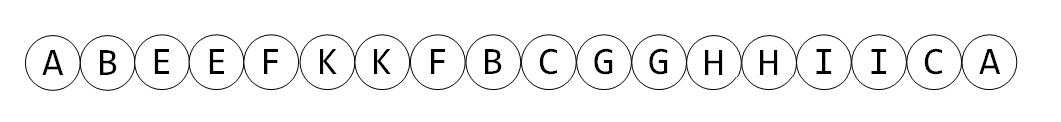
性质
DFS 序列有一些非常有用的性质:
- 如果一个点的起始时间和终结时间被另一个点包括,这个点肯定是另一个点的子节点。(简称括号化定理)
- 一颗子树的所有节点在 DFS 序内是连续的一段;
- 对于求任意点对 (a,b)(a,b) 之间的路径的问题,可分为两种情况,首先是令 lcalca 是 a,ba,b 的最近公共祖先:
- 若 lcalca 是 a,ba,b 之一,则 a,ba,b 之间的 inin 时刻的区间或者 outout 时刻区间就是其路径。例如
AK之间的路径就对应区间ABEEFK或者KFBCGGHHIICA。 - 若 lcalca 不为 aa 或 bb ,则 a,ba,b 之间的路径为 In[a]In[a] 、 Out[b]Out[b] 之间的区间或者 In[b]In[b] 、 Out[a]Out[a] 之间的区间。另外,还需额外加上 lcalca 。比如上图中的
EK路径,对应为EFK再加上B。考虑EH之间的路径,对应为EFKKFBCGGH再加上A。
- 若 lcalca 是 a,ba,b 之一,则 a,ba,b 之间的 inin 时刻的区间或者 outout 时刻区间就是其路径。例如
我们发现,一个点的进出栈的时间点之间的时间段就是它的子树在栈中的所有时间。也就是说,子树的 DFS 序肯定大于根节点的进栈时间小于根节点的出栈时间,这就成了一个 区间问题 。所以我们就把一个树上的问题转换到了一个线性的数据结构上面。区间问题就比较好做了,有各种强大的数据结构可以用来维护区间,例如线段树,树状数组。然后我们可以 随便搞了 。
因为我们发现每个节点在 DFS 序中均会出现 22 次,第一次是进入 DFS 的时刻,第二次是离开 DFS 的时刻。分别称之为 inin 与 outout 。在区间操作中,如果某个节点出现了 22 次,则该节点将会出现被“抵消”。所以通常会将 outout 时刻对应的点设置为 负数 。那么, 根节点到任意节点的权值和就是 DFS 序上对应的一个前缀和 。
利用这些性质,可以利用 DFS 序列完成子树操作和路径操作,同时也有可能将莫队算法应用到树上从而得到树上莫队。
时间戳
时间戳是 DFS 序的另外一种形式,它记录第节点的一次 开始 访问这个点的时间和和最后 结束 访问的时间。
void dfs(int u, int fa) {seq[++cnt] = u; // 记录 dfs 序列in[u] = cnt;for(auto v : g[u]) {if(v == fa) continue;dfs(v, u);}// seq[++cnt] = u; // 和标准 DFS 序列不同,时间戳不重复保存元素out[u] = cnt;// siz[u] = out[u] - in[u] + 1; // 子树元素数量
}
练习题:P4785 树的 DFS - TopsCoding
模板题
模板题:P4065 DFS 序 1 - TopsCoding
思路:
我们考虑 DFS 序的另外一种形式,当访问到一个节点时记下当前的时间戳,我们设它为 in[x]in[x] ,结束访问一个节点时当前的时间戳设为 out[x]out[x] 。
则以 xx 为根的子树刚好是 in[x]in[x] 和 out[x]out[x] 中间的点。我们看下面这个例子。
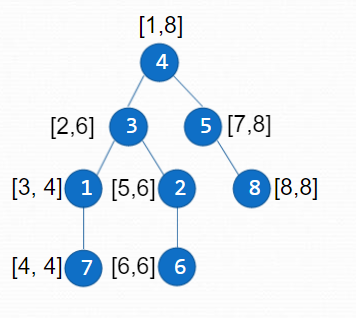
有了DFS序这个性质我们就可以将这个问题转化成一个区间求和问题。每一次询问的复杂度就是 O(logn)O(logn) 级别
的,完全可以接受。
练习题
- P4785 树的 DFS - TopsCoding —— 热身题
- P4065 DFS 序 1 - TopsCoding —— 模板题
- P4066 DFS 序 2 - TopsCoding —— 区间修改+区间查询
- P4769 「一本通 4.5 练习 1」树上操作 - TopsCoding ——
树链剖分
引入
我们已经学会了利用 DFS 序将树上子树的操作转化成区间操作了,所以思考如何将链也转化成一个个区间,这就需要用到树链剖分了。
我们可以发现, 在 DFS 序中,也存在一些链是连续的 ,所以我们可以思考怎样利用这些链( 这就是树链剖分的思想 )。
可以将每一条链存起来,如果直接进行操作,会快一点,但是依然不够,所以要继续优化。
因为我们直接对整条连续链操作,所以尝试让操作次数更多的链长度更长,发现链的尾部子树越大,操作次数可能越多。
所以让连续的链尽量向子树大的儿子延伸,是最优的。这就是树链剖分中, 重链剖分 的思想。
简介
树链剖分的核心思想:将树上的节点重新编号并转化为一条链(DFS 序),使得树上的任意一条路径,都可以转化为该 树链 上的 O(logn)O(logn) 段的连续区间。这样树上路径的问题,就可以转化成区间上的问题。转化为区间问题后,就可以用线段树、树状数组等数据结构来处理。
重难点:
- 如何将树转化为一个序列;
- 如何将树上的路径转化为不超过 lognlogn 段的连续区间。
树链剖分通常用于解决一些维护静态树上路径信息的问题,如:
- 修改 树上两点之间的路径上 所有点的值;
- 查询 树上两点之间的路径上 节点权值的 和/极值/其它(在序列上可以用数据结构维护,便于合并的信息) ;
- 修改 树上某节点的子树内的所有节点 ;(DFS 序上的修改)
- 查询 树上某节点的子树内的所有节点的和/极值/其他 。(DFS 序上的查询)
除了配合数据结构来维护树上路径信息,树剖还可以用来 O(logn)O(logn) (且 常数较小 )地求 LCA。在某些题目中,还可以利用其性质来灵活地运用树剖。
具体来说,树链剖分的思想是将整棵树剖分为若干条链,使它组合成线性结构,然后用其他的数据结构维护信息。
树链剖分的核心重难点是如何恰当地将树剖分成若干条链。当链的划分方式确定后,我们只要将它们看做是一个个序列,将所有序列按顺序拼接起来,每条链就成为了一段区间,而序列上的区间问题就是我们所熟悉和擅长解决的了。
剖分有多种形式,如 重链剖分 , 长链剖分 和用于 Link/cut Tree 的剖分(有时被称作“实链剖分”),大多数情况下(没有特别说明时),“树链剖分”都指“重链剖分”。
重链剖分
重链剖分可以将树上的任意一条路径划分成不超过 O(logn)O(logn) 条连续的链,每条链上的点深度互不相同(即是自底向上的一条链,链上所有点的 LCA 为链的一个端点)。
重链剖分还能保证划分出的每条链上的节点 DFS 序连续,因此可以方便地用一些维护序列的数据结构(如线段树)来维护树上路径的信息。
基本的定义
我们给出重链剖分中的一些基本的定义:
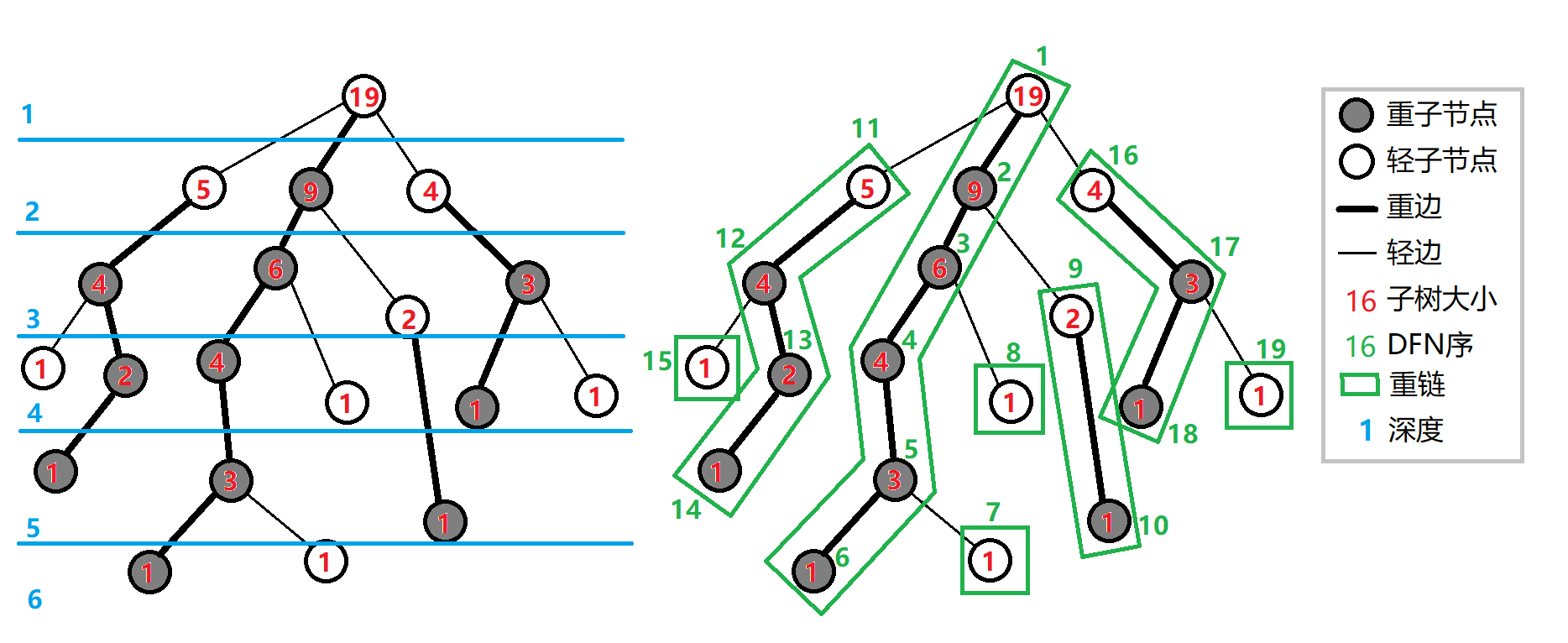
重儿子/重子节点 :表示其子节点中子树最大的子结点。如果有多个子树最大的子结点,任取其一即可。如果没有子节点,就无重子节点。
轻儿子/轻子节点 :对于父节点,除重儿子外剩余的所有子结点就是其轻儿子,根节点是轻儿子。
重边 :父节点到重子节点的边为 重边 。
轻边 :父节点到轻子节点的边为 轻边 。
重链/重路径 :若干条首尾衔接的 重边 构成 重链 ,特殊地, 落单的结点也当作重链 。
那么整棵树就被剖分成若干条重链,然后我们在深度优先遍历地时候,记录各个节点的访问编号( DFSDFS 序),并且在访问一个节点的所有儿子时, 最先访问它的重儿子 ,这样一来就有如下结论:
- 重儿子在从其父节点往下的重链中;
- 每一条重链都以轻儿子作为起点;
- 对于叶子节点,若其为轻儿子,则有一条以自己为起点的长度为 11 的链(落单的结点构成的重链)。
- 每条重链上的节点编号在 DFSDFS 序中是连续的
如图:

基本的性质
我们以任意点为根,然后记 size(u)size(u) 为以 uu 为根的子树的节点个数,那么有如下几个性质:
性质 11 : 如果 (u,v)(u,v) 为轻边,则 size(v)≤size(u)/2size(v)≤size(u)/2 。
证明:反证法。假设 size(v)>size(u)/2size(v)>size(u)/2 ,则 size(v)size(v) 必然比其他儿子的 sizesize 要大,那么 (u,v)(u,v) 必然为重边,这与 (u,v)(u,v) 是轻边矛盾,所以假设不成立。
性质 22 :从根到某一点 vv 的路径上的轻边个数不多于 O(logn)O(logn) 。
证明: vv 为叶子节点时轻边数量最多。由性质 11 可知,每经过一条轻边,子树的节点个数至少减少一半,因此,至多经过 O(logn)O(logn) 条轻边就到达叶子节点。
性质 33 :对于每个点到根的路径上都有不超过 O(logn)O(logn) 条轻边和 O(logn)O(logn) 条重链。
证明:显然,这条路径可以划分重链和轻边的交错序列,即一条重链、一条轻边、一条重链、一条轻边、......、最后一条重链(可能是不完整)。而由性质 22 可知,路径上的轻边的条数为 O(logn)O(logn) ,所以重链的条数也为 O(logn)O(logn) 。
性质4 :所有的重链将整棵树 完全剖分 ,不会有节点遗漏。
证明:因为除叶子节点外,每个节点都有一个重儿子,所以对于除叶子节点外的所有点,从其往下必然有一条重链。而是重儿子的叶节点必然在一条重链内,是轻儿子的叶节点单独成为一条重链。因此,得证。
性质5 :将整棵树剖分成若干条重链后,树中任意一条路径 (u,v)(u,v) 均可拆分成 O(logn)O(logn) 条重链,也即 O(logn)O(logn) 个连续区间。
证明:我们可以分别处理 u,vu,v 两个点到其最近的公共祖先的路径,根据性质 33 ,这条路径分解成最多 O(logn)O(logn) 条的重链和最多 O(logn)O(logn) 条轻边。 如此,我们只需要考虑如何维护这两种对象。
DFS 序列
在剖分时 重边优先遍历 ,最后树的 DFSDFS 序上,重链内的 DFSDFS 序是连续的,且所有的重链将整棵树 完全剖分 。因此,按 DFSDFS 排序后的序列即为整棵树剖分后的链。
对于重链,因为使用如上的 DFSDFS 序,因此,此时重链相当于一个区间,我们只需用线段树(树状数组等亦可)来维护。而对于轻边,我们可以直接跳过,访问下一条重链。为什么呢?因为轻边的两个端点一定在某两条重链上。这两种操作的时间复杂度分别为 O(log2n)O(log2n) 和 O(logn)O(logn) ,因此总复杂度为 O(log2n)O(log2n) 。
轻重剖分的过程可以用两次 dfs 实现,有时为了防止栈溢出,也可以用 bfs 实现,下面介绍如何实现。
实现
模板题:P4780 树链剖分 I - TopsCoding
剖分过程中要用到如下 77 个值:
- fa(x)fa(x) 表示节点 xx 在树上的父亲。
- dep(x)dep(x) 表示节点 xx 在树上的深度。
- siz(x)siz(x) 表示节点 xx 的子树的节点个数。
- son(x)son(x) 表示节点 xx 的 重儿子 。
- top(x)top(x) 表示节点 xx 所在 重链 的顶部节点(深度最小)。
- seg(x)seg(x) 表示节点 xx 的 DFS 序 ,也是其在线段树中的编号。
- rev(i)rev(i) 表示 DFS 序中第 ii 个元素所对应的节点编号,有 rev(seg(x))=xrev(seg(x))=x 。
1. 预处理
第一个 dfsdfs ,预处理上面的前 44 个值:所有节点的 重儿子 son(u)son(u) 以及 子树节点的数量 siz(u)siz(u) 和 每个节点的 父节点 fa(u)fa(u) 。
void dfs1(int u, int f) {fa[u] = f; dep[u] = dep[f] + 1;siz[u] = 1;for(auto v : g[u]) {if(v != f) {dfs1(v, u);siz[u] += siz[v];if(siz[son[u]] < siz[v]) // 更新重儿子son[u] = v;}}
}
2. 树链剖分
第一个 dfsdfs ,预处理上面的后 33 个值:节点所在重链的 链顶 ( top(u)top(u) ,应初始化为结点本身)、重边优先遍历时的 DFS 序 ( seq(u)seq(u) )、DFS 序对应的 节点编号 ( rev(u)rev(u) )。
void dfs2(int u, int t) { // t: 重链链顶seg[++cnt] = u;rev[u] = cnt; nw[cnt] = a[u]; // nw[]: 新的节点编号对应的权值top[u] = t;if(!son[u]) return; // 是叶子节点dfs2(son[u], t); // 优先对重儿子进行 DFS,可以保证同一条重链上的点 DFS 序连续for(auto v : g[u]) {if(v == fa[u] || v == son[u]) continue;dfs2(v, v); // 新的重链的开头,top[v] = v}
}
3. 更新/查询
问题:如何将一条路径转化成需要的 O(logn)O(logn) 个区间?
思路:类似爬山法求最近公共祖先。通过重链向上爬,找到最近公共重链,最后加上在 相同重链 里的区间部分,如下图所示:
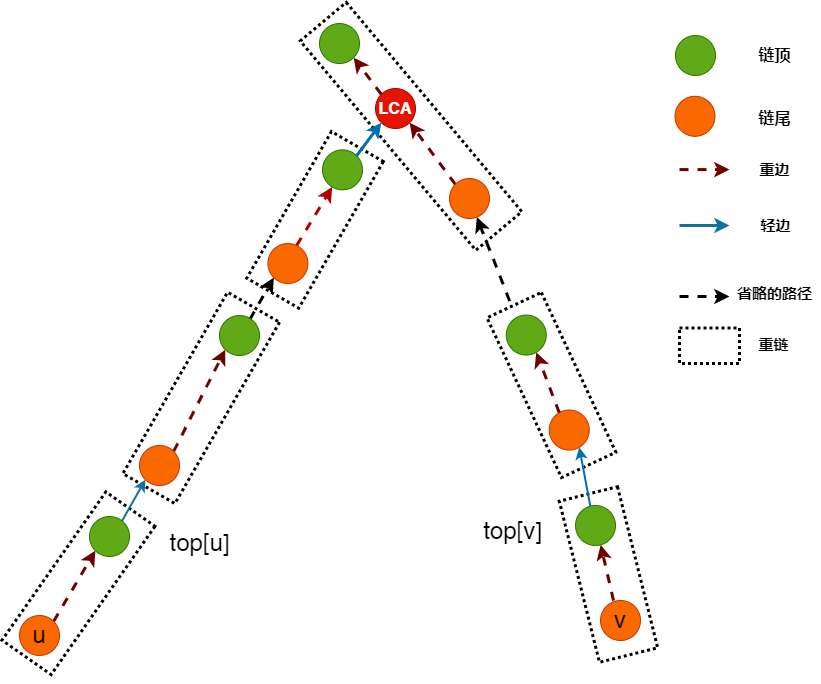
修改这些区间 维护的信息 的时间复杂度为 O(logn)O(logn) (分块来维护的话是 nn )
类型1. 维护树上两点间的路径
思路即上面的爬山法。
// 修改:u,v 间路径上各点权值增加 k
void update_path(int u, int v, int k) {while(top[u] != top[v]) { // 还没跳到同一条重链上if(dep[top[u]] < dep[top[v]]) swap(u, v); // 找到链顶更深的那条链update(1, rev[top[u]], rev[u], k); // 区间更新其中深度更深的重链上的权值u = fa[top[u]];}if(dep[u] < dep[v]) swap(u, v); // 最后一条不完整的重链,保证 v 是 u 的祖先update(1, rev[v], rev[u], k); // 在同一重链中,处理剩余区间
}
// 查询同理
LL query_path(int u, int v) {LL res = 0;while(top[u] != top[v]) {if(dep[top[u]] < dep[top[v]]) swap(u, v);res += query(1, rev[top[u]], rev[u]) % mod; // 累加当前更深的重链上的权值和u = fa[top[u]];}if(dep[u] < dep[v]) swap(u, v);res += query(1, rev[v], rev[u]) % mod; // 累加剩余区间和return res % mod;
}
类型2. 维护树上节点的子树
根据 DFS 序的性质,子树在 DFS 序上是连续的,直接利用 DFS 序的 rev[]rev[] 和 siz[]siz[] 确定子树对应的区间范围后,进行区间修改/区间查询即可。
void update_tree(int u, int k) {update(1, rev[u], rev[u]+siz[u]-1, k); // 利用子树 DFS 序连续处理即可
}
LL query_tree(int u) {return query(1, rev[u], rev[u]+siz[u]-1) % mod; // 利用子树 DFS 序连续处理即可
}
4. 完整示例代码
模板题:P4780 树链剖分 I - TopsCoding
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 1e5+5;
int n, m, root, mod, a[N], nw[N];
vector<int> g[N];
int seg[N], rev[N], cnt; // DFS 序列
int dep[N], fa[N], siz[N], son[N], top[N]; // 树剖
struct Tree{ // 线段树int l, r;LL tag, sum;
} tr[N<<2];
/********** 预处理部分 **********/
void dfs1(int u, int f) {fa[u] = f; dep[u] = dep[f] + 1;siz[u] = 1;for(auto v : g[u]) {if(v != f) {dfs1(v, u);siz[u] += siz[v];if(siz[son[u]] < siz[v])son[u] = v;}}
}
void dfs2(int u, int t) {seg[++cnt] = u; nw[cnt] = a[u];rev[u] = cnt;top[u] = t;if(!son[u]) return; // 是叶子节点dfs2(son[u], t); // 优先对重儿子进行 DFS,可以保证同一条重链上的点 DFS 序连续for(auto v : g[u]) {if(v == fa[u] || v == son[u]) continue;dfs2(v, v);}
}
/********** 线段树部分 **********/
void push_up(int p) {tr[p].sum = tr[p*2].sum + tr[p*2+1].sum;
}
void push_down(int p) {if(!tr[p].tag) return;auto < = tr[p*2], &rt = tr[p*2+1];lt.tag += tr[p].tag;rt.tag += tr[p].tag;lt.sum += tr[p].tag * (lt.r - lt.l + 1);rt.sum += tr[p].tag * (rt.r - rt.l + 1);tr[p].tag = 0;
}
void build(int l, int r, int p) {tr[p] = {l, r, 0, nw[l]};if(l == r) return;int mid = (l+r) / 2;build(l, mid, p*2);build(mid+1, r, p*2+1);push_up(p);
}
void update(int p, int ql, int qr, int k) {if(ql <= tr[p].l && tr[p].r <= qr) {tr[p].tag += k;tr[p].sum += k * (tr[p].r - tr[p].l + 1);return;}push_down(p);int mid = (tr[p].l + tr[p].r) / 2;if(ql <= mid) update(p*2, ql, qr, k);if(mid < qr) update(p*2+1, ql, qr, k);push_up(p);
}
LL query(int p, int ql, int qr) {if(ql <= tr[p].l && tr[p].r <= qr) return tr[p].sum;push_down(p);int mid = (tr[p].l + tr[p].r) / 2;LL res = 0;if(ql <= mid) res += query(p*2, ql, qr) % mod;if(mid < qr) res += query(p*2+1, ql, qr) % mod;return res % mod;
}
/********** 路径/子树更新和查询部分 **********/
void update_path(int u, int v, int k) {while(top[u] != top[v]) {if(dep[top[u]] < dep[top[v]]) swap(u, v); // 找到链顶更深的那条链update(1, rev[top[u]], rev[u], k); // 更新其中深度更深的重链上的权值u = fa[top[u]];}if(dep[u] < dep[v]) swap(u, v); // 最后一条不完整的重链update(1, rev[v], rev[u], k);
}
LL query_path(int u, int v) {LL res = 0;while(top[u] != top[v]) {if(dep[top[u]] < dep[top[v]]) swap(u, v);res += query(1, rev[top[u]], rev[u]) % mod; // 更新其中深度更深的重链上的权值u = fa[top[u]];}if(dep[u] < dep[v]) swap(u, v); // 最后一条不完整的重链res += query(1, rev[v], rev[u]) % mod;return res % mod;
}
void update_tree(int u, int k) {update(1, rev[u], rev[u]+siz[u]-1, k); // 利用子树 DFS 序连续处理即可
}
LL query_tree(int u) {return query(1, rev[u], rev[u]+siz[u]-1) % mod; // 利用子树 DFS 序连续处理即可
}
int main(){ios::sync_with_stdio(0);cin.tie(0);cin >> n >> m >> root >> mod;for(int i = 1; i <= n; i++) cin >> a[i];for(int i = 1, u, v; i < n; i++) {cin >> u >> v;g[u].push_back(v);g[v].push_back(u);}dfs1(root, 0);dfs2(root, root);build(1, n, 1);while(m--) {int op, u, v, k;cin >> op >> u;if(op == 1) {cin >> v >> k;update_path(u, v, k);} else if(op == 2) {cin >> v;cout << query_path(u, v) << '\n';} else if(op == 3) {cin >> k;update_tree(u, k);} else {cout << query_tree(u) << '\n';}}return 0;
}
时间复杂度和常数分析
树链剖分主要操作的复杂度分析如下:
- 预处理:第一次深度优先遍历,复杂度为 O(n)O(n) ;
- 树链剖分:第二次深度优先遍历,复杂度为 O(n)O(n) ;
- 子树更新/查询:直接为线段树的更新/查询,所以复杂度为 O(logn)O(logn) ;
- 路径更新/查询:根据重链剖分的性质 55 ,树中任意一条路径 (u,v)(u,v) 均可拆分成 O(logn)O(logn) 条重链,也即 O(logn)O(logn) 个连续区间,每条重链的修改的时间复杂度为 O(logn)O(logn) ,因此总复杂度为 O(log2n)O(log2n) 。
可以看出,树链剖分的整体复杂度是非常低的,且注意到,在进行路径更新时,虽然总复杂度为 O(log2n)O(log2n) ,但是重链的条数和平均每条重链的长度是成反比的。因此,树链剖分的常数其实是非常小的。
常见应用
路径上维护
用树链剖分求树上两点路径权值和,伪代码如下:
TREE-PATH-SUM (u,v)1tot←02while u.top is not v.top3if u.top.deep<v.top.deep4SWAP(u,v)5tot←tot+sum of values between u and u.top6u←u.top.father7tot←tot+sum of values between u and v8return totTREE-PATH-SUM (u,v)12345678tot←0while u.top is not v.topif u.top.deep<v.top.deepSWAP(u,v)tot←tot+sum of values between u and u.topu←u.top.fathertot←tot+sum of values between u and vreturn tot
链上的 DFS 序是连续的,可以使用线段树、树状数组维护。
每次选择深度较大的链往上跳,直到两点在同一条链上。
同样的跳链结构适用于维护、统计路径上的其他信息,比如最大值、最小值等。
子树维护
有时会要求,维护子树上的信息,譬如将以 uu 为根的子树的所有结点的权值增加 kk 。
在 DFS 搜索的时候,子树中的结点的 DFS 序是连续的。
我们只需记录每个节点对应子树的大小 siz[]siz[] ,那么 [rev[u],rev[u]+siz[u]−1][rev[u],rev[u]+siz[u]−1] 就表示 uu 所在子树的连续区间。
这样就把子树信息转化为连续的一段区间信息。
求最近公共祖先
不断向上跳重链,当跳到同一条重链上时,深度较小的结点即为 LCA。
向上跳重链时需要先跳所在重链顶端深度较大的那个。
参考代码:
int lca(int u, int v) {while (top[u] != top[v]) {if (dep[top[u]] > dep[top[v]])u = fa[top[u]];elsev = fa[top[v]];}return dep[u] > dep[v] ? v : u;
}
练习题
- P4780 树链剖分 I - TopsCoding —— 模板题
- P4732 「一本通 4.5 例 1」树的统计 Count
- P4070 最近公共祖先(LCA)——(树剖求 LCA 无需数据结构,可以用作练习)
- P4769 「一本通 4.5 练习 1」树上操作
- P4779 「JLOI2014」松鼠的新家 —— (当然也可以用树上差分)
- P4781 树链剖分 II - TopsCoding —— 换根
- P4770 「NOI2015」软件包管理器
- P4771 「一本通 4.5 练习 3」染色
- P4772 SDOI2014 旅行
- P4783 「POI2014」酒店 Hotel 加强版
