基于多策略混合改进哈里斯鹰算法的混合神经网络多输入单输出回归预测模型HPHHO-CNN-LSTM-Attention
基于多策略混合改进哈里斯鹰算法的混合神经网络多输入单输出回归预测模型HPHHO-CNN-LSTM-Attention
在现代数据科学领域,回归预测模型在很多应用场景中都扮演着重要角色。无论是经济预测、气候建模还是金融风险分析,准确的回归模型都至关重要。然而,如何提高模型的准确性和泛化能力,仍然是许多研究者面临的挑战。本文将探讨一种新的回归预测模型——基于多策略混合改进哈里斯鹰算法的混合神经网络多输入单输出回归预测模型,简称HPHHO-CNN-LSTM-Attention。
1. 模型概述
HPHHO-CNN-LSTM-Attention模型结合了多个先进的算法与神经网络架构,旨在优化回归任务的预测精度。该模型的核心思想是利用哈里斯鹰优化算法(Harris Hawks Optimization, HHO)和混合神经网络(CNN-LSTM-Attention)相结合,通过多策略优化改进哈里斯鹰算法,进一步提升模型性能。
1.1 哈里斯鹰优化算法(HHO)
哈里斯鹰优化算法是一种模拟鹰捕猎行为的优化算法,通常用于求解复杂的优化问题。它具有良好的全局搜索能力和较强的收敛性。但在实际应用中,单一的HHO算法可能会面临局部最优解的问题,因此,我们提出了“多策略混合改进”的概念,通过引入不同的优化策略,增强了算法的搜索能力和稳定性。
1.2 混合神经网络(CNN-LSTM-Attention)
在特征提取和时间序列建模方面,卷积神经网络(CNN)和长短期记忆网络(LSTM)已被广泛应用于各种预测任务。CNN能够有效地从输入数据中提取空间特征,而LSTM则擅长处理时序数据中的长期依赖关系。此外,注意力机制(Attention)通过为不同时间步的输入分配不同的权重,使得模型能够更加关注关键时刻的输入信息,进一步提升预测效果。
2. 多策略混合改进哈里斯鹰算法
为了克服传统HHO算法的局限性,提出了“多策略混合改进”的概念。通过这种混合方式,HPHHO算法能够在复杂的回归问题中找到更优的解,避免陷入局部最优解。同时,改进后的算法能够更快速地收敛,提高了整体计算效率和优化精度。
3. HPHHO-CNN-LSTM-Attention模型的工作原理
该模型的基本工作流程如下:
-
数据预处理:首先,对输入数据进行标准化和归一化处理,确保数据适合神经网络的训练。
-
特征提取(CNN):使用卷积神经网络(CNN)提取输入数据的空间特征。在此阶段,模型通过卷积层和池化层,从输入数据中学习到重要的局部特征。
-
时序建模(LSTM):通过长短期记忆网络(LSTM),捕捉输入数据中的时序依赖关系。LSTM网络能够有效地处理时间序列数据中的长期依赖性,适用于处理动态变化的回归任务。
-
注意力机制(Attention):引入注意力机制,赋予不同时间步的输入数据不同的权重,从而增强模型对关键信息的关注,提高预测精度。
-
优化算法(HPHHO):最后,通过基于多策略混合改进的哈里斯鹰算法(HPHHO)对模型进行优化,进一步提升模型的性能。
4. 模型优势
-
提高准确性:通过多种优化策略的结合,HPHHO算法能够帮助模型在全局最优解附近找到更加精确的解,从而显著提升回归预测的准确性。
-
增强鲁棒性:混合神经网络架构(CNN-LSTM-Attention)使得模型具备了对复杂数据的强大拟合能力,能够处理非线性、时序性的复杂问题。
-
高效性:改进后的哈里斯鹰优化算法能够更快速地收敛,减少训练时间,同时避免了局部最优解的困扰。
-
适用广泛:该模型不仅适用于回归任务,还能够扩展到其他机器学习问题,如分类、聚类等。
5. 实际应用
HPHHO-CNN-LSTM-Attention模型的应用场景非常广泛,尤其适用于那些具有复杂特征和时序依赖的回归预测问题。例如,气候预测、股票市场分析、交通流量预测等领域都可以受益于这一模型。
6. 总结
基于多策略混合改进哈里斯鹰算法的混合神经网络多输入单输出回归预测模型(HPHHO-CNN-LSTM-Attention)不仅在优化算法上进行了创新,同时在神经网络架构上也做了融合创新,极大地提升了回归预测的精度和效率。随着人工智能技术的不断发展,类似的混合优化模型将在未来的预测任务中发挥更大的作用,推动相关领域的技术进步。
7.部分代码
warning off % 关闭报警信息
close all % 关闭开启的图窗
clear % 清空变量
clc % 清空命令行
tic
rng('default');
tic%% 导入数据
res = xlsread('data.xlsx');%% 数据分析
num_size = 0.7; % 训练集占数据集比例
outdim = 1; % 最后一列为输出
num_samples = size(res, 1); % 样本个数
%res = res(randperm(num_samples), :); % 打乱数据集(不希望打乱时,注释该行)
num_train_s = ceil(num_size * num_samples)+1; % 训练集样本个数
f_ = size(res, 2) - outdim; % 输入特征维度%% 划分训练集和测试集 前70%训练,后30%测试
P_train = res(1: num_train_s, 1: f_)';
T_train = res(1: num_train_s, f_ + 1: end)';
M = size(P_train, 2);P_test = res(num_train_s + 1: end, 1: f_)';
T_test = res(num_train_s + 1: end, f_ + 1: end)';
N = size(P_test, 2);%% 数据归一化
[p_train, ps_input] = mapminmax(P_train, 0, 1);
p_test = mapminmax('apply', P_test, ps_input);[t_train, ps_output] = mapminmax(T_train, 0, 1);
t_test = mapminmax('apply', T_test, ps_output);%% 数据平铺
% 将数据平铺成1维数据只是一种处理方式
% 也可以平铺成2维数据,以及3维数据,需要修改对应模型结构
% 但是应该始终和输入层数据结构保持一致
p_train = double(reshape(p_train, f_, 1, 1, M));
p_test = double(reshape(p_test , f_, 1, 1, N));
t_train = double(t_train)';
t_test = double(t_test )';%% 数据格式转换
for i = 1 : MLp_train{i, 1} = p_train(:, :, 1, i);
endfor i = 1 : NLp_test{i, 1} = p_test( :, :, 1, i);
end
8.运行结果


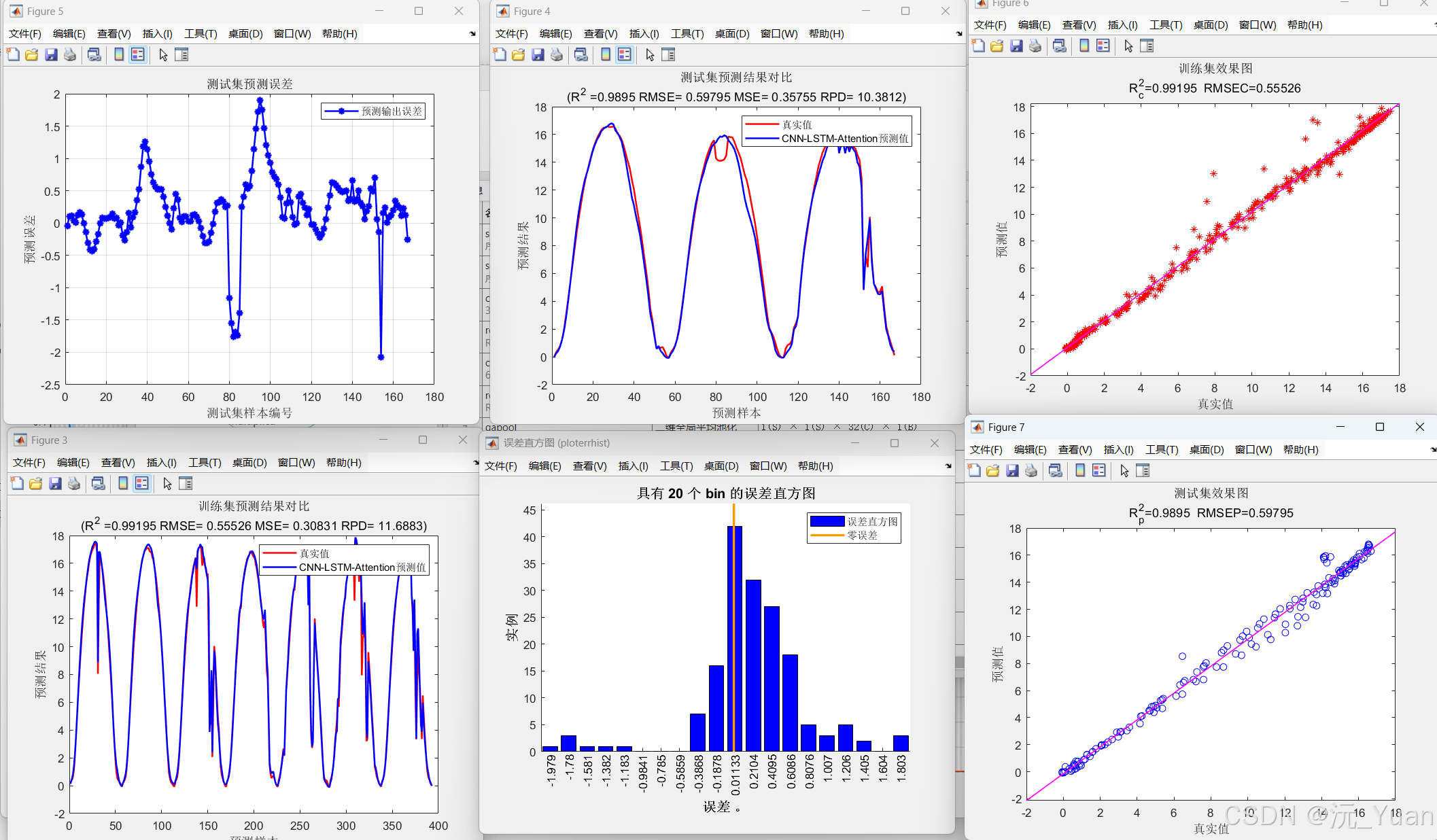

代码下载
https://mbd.pub/o/bread/aZ6blZ1p
