AVL树(2):
我们之前讲AVL树,我们讲到了旋转,然后讲了左单旋和右单旋。
但是我们这里的单旋产生的条件都是纯粹的一边比较高,

我们看上面这个图片,当我们插入新的结点导致一边的子树比较高的时候,我们必须是存粹的一边高,和图片上面的几个一样,图片下面的几个就不行。
我们看图片中下面的,当我们插入一个结点,结点里面的key(可能是存单个数据的搜索二叉树set,也可能是存一对数据的搜索二叉树,但是维持我们的搜索二叉树的本质的还是要看我们的key)比我们的5大的时候,这时候我们把他插入到我们的5结点的右子树的位置上。这时候他就不是我们的存粹的一边高了。这时候我们看他的根节点的左子树比右子树要高,根节点的平衡因子就是-2,这时候虽然左边子树高度有问题,但是我们不能直接的进行右旋,他不满足我们的“存粹的一边高”。
所以面对这种情况,我们就要学习新的旋转了;
左右双旋:

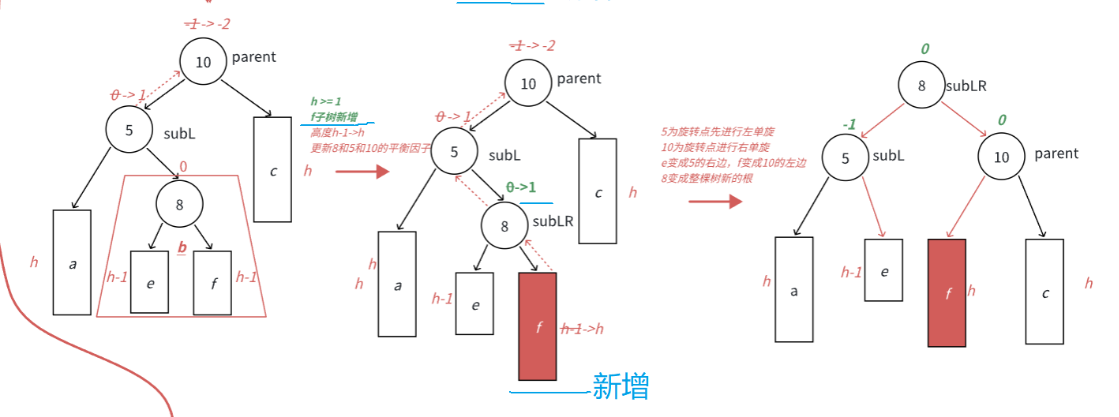
这个是我们的左右双旋的抽象图;
首先看当我们的h高度为0的时候:

我们看这个图片:开始的时候,我们是右10和5两个结点,然后我们这时候要给二叉树插入一个新的结点,结点的大小比5要大,这时候他就被插入到5结点的右边去了。
这时候我们的10结点的平衡因子是-2,这时候平衡因子出了问题,我们就要进行旋转,我们先看根节点10的左子树,这棵的右边是冗余的,这时候我们把5这个结点作为我们的旋转点进行左旋,左旋后的结果是我们的第三个图片,这时候它就变成单纯的一边高了,这时候我们就把10最为我们的旋转点,然后进行一个右旋,这时候得到我们的最后一个图片;
我们再看当我们的h等于1的时候:

最左边的是我们的开始时候的图片,然后我们插入一个结点,这个结点插入到我们的b结点的右边了,然后这时候因为他不是一个单纯的一边比较高,这时候我们就使用一个左右双旋,我们先使用左旋,再使用一个右旋;
我们看根节点10的左子树,5这棵树的右边比较高,我们就使用一个左旋,然后得到我们的第三个图片,,然后我们再以我们的根节点10作为我们的旋转点,进行一个右旋得到我们的第四个图片;
平衡因子的调节:
当我们进行了左右双旋,其实就是进行了左旋,再进行右旋,我们上期的时候,我们学习了左单旋和右单旋,我们的单旋的代码最后,我们会把parent和subL的平衡因子置为0;
但是我们的双旋之后,我们的parent和subL的平衡因子不一定是0;这时候,我们就要主动的去改变他的平衡因子,这就要分为几种情况了;

我们看这个图片:我们给5结点的右子树插上一个结点,这时候我们给5结点进行左旋,这时候要把b子树给拆开来看,不然的话,不能达到我们的左旋的逻辑;
这个时候,我们就要分情况来进行讨论了。
第一种:

我们把b子树拆开,把高度为h的树分成一个结点和两个高度为h-1的树,然后在e树上插入一个结点,e树的高度变回h,然后我们进行左右双旋,得到最后一个图片的树。
第二种:
我们给f子树插入结点;然后,,,最后得到我们的第三个数;
第三种:

当我们的h等于0的情况;
这三种情况最后得到的树,里面的平衡因子都是不同的,需要我们手动的按照结果去修改;
理解:

当我们的平衡因子出现问题,我们需要进行旋转,我们先看我们的比较高的子树,这个图片里面就是我们的左子树,左子树的右边子树比较冗余,我们就在左子树上进行一个左旋,完后整棵树的左边的数据比较冗余,我们这时候就给整棵树进行一个右旋。
我们看我们的左右双旋的抽象图,我们的左右双旋就是要把8那个结点作为我们的调节完后的根节点,然后8的左子树变成我们的5的右子树,8的右子树变成我们的10的左子树。
然后5结点变成我们的8的左节点,10结点作为我们8的右节点;
左右双旋的代码的实现:


我们的左右双旋对我们的左单旋和右单旋实行了复用,我们看代码实现,我们判断他是在哪个树插入的,我们就看8结点的平衡因子;8结点的平衡因子是1的时候,就是f子树的插入,8结点的平衡因子是-1的时候,就是e子树的插入,当然只会是这两个树,如果是a树的话,那就不是左右双旋了;
右左双旋:

这个是我们的右左双旋的抽象图:
我们给我们的b子树插入一个结点,然后这时候我们的10结点的平衡因子变成了2,这时候我们就要进行旋转调整;
我们看我们的总的树的右子树,右子树的左子树数据比较冗余,我们给右子树来一个右旋,然后结束后,总的这棵树右边的数据比较冗余,这时候我们就给整棵树一个来一个左旋。
平衡因子:
右左双旋和左右双旋是比较类似的,平衡因子的调节也是要分为三种情况的,我们要把b子树拆开,然后分成三种情况;,,,最后再根据调整完后的树来修改我们的平衡因子;
第一种:

这个就是我们的其中的一种,我们插入的结点在f树上。我们实现完后手动的修改我们的平衡因子;
第二种:

这次我们插入结点的位置在f树上。
第三种:

这个是我们的第三种h为0的时候的情况;
我们的这三种情况最后的树里面的parent,subL,subR这三个结点的平衡因子都不一样;
实现的时候我们就要分情况手动的修改他。
理解:

我们的右左双旋要把12结点作为我们的根节点,12的左子树作为10的右子树,12的右子树作为15的左子树,然后10作为12的左结点,15作为12的右节点;
右左双旋的代码的实现:

右左双旋和左右双旋都是我们的单旋的复用。
AVL树的查找:

我们输入一个key,当然我们也可以是输入一对数据,然后我们进行查找,找到的话就返回这个位置的指针,没找到就返回空指针。
AVL树的删除:

AVL树的删除,当我们删除一个结点的时候,我们就让这个结点的父亲指向我们的这个结点的孩子,然后把这个结点删除,这个结点删除以后,我们要更新我们的平衡因子,我们看第一个图片,当我们要删除7结点的时候,我们让6结点指向我们的7结点的孩子结点,然后修改6结点的平衡因子,我们的6结点的平衡因子,从0变成了-1,这时候,我们可以停止更新我们的平衡因子了,因为没有什么改变,我们的二叉树的高度没有发生变化。我们的6结点有两个孩子,删除一个后高度没有变化,所以,当我们的平衡因子由0变成1或者是-1的时候,这时候我们就可以停止更新我们的平衡因子了,但是如果是1或者-1变成了0,这时候我们就要再不断地更新平衡因子;
看右边的二叉树,我们删除14的结点以后,8结点的平衡因子变成-2,这时候这个二叉树就要旋转。左右双旋。
