【数据分享】上市公司-创新投入、研发投入数据(2007-2022)
数据介绍
在当今竞争激烈的商业环境中,企业的创新投入和研发投入对于其生存和发展至关重要。创新投入是企业通过改进、完善或引入全新产品来满足市场需求,并取得竞争优势的过程。而研发投入则是企业为了推动产品创新而进行的资源投入,涵盖人力、物力、财力等多个方面。今天,我们将为大家分享一份关于上市公司创新投入和研发投入的数据,旨在为相关研究和分析提供有力支持。
一、数据简介
这份数据名为 “上市公司 - 创新投入、研发投入数据”,时间跨度为 2007 - 2022 年,具有很高的时间完整性和连贯性,能够为长期的趋势分析提供丰富的素材。数据中包含了 36,792 条观测值,涉及多个关键指标。
其中,研发支出与当期 / 上期总资产之比、研发支出与当期 / 上期营业收入之比,这几个指标从不同的财务角度衡量了企业研发投入的规模和强度。通过与总资产和营业收入的对比,可以清晰地看到企业在研发上的投入相对于其整体规模和经营成果的占比情况。创新投入增长率则直观地反映了企业创新投入的动态变化,让我们能够了解企业在不同时期创新投入的增长速度。研发投入是否增加 (虚拟变量) 这一指标则以简洁的方式表明企业在研发投入上的增减情况,方便进行分类分析和对比研究。
二、相关数据
除了上述核心指标外,数据中还包含了大量有助于全面了解上市公司情况的相关信息。从公司基本信息来看,有股票代码简称缩略、股票代码、年度、股票简称等,这些信息能够准确地定位每一家上市公司,并跟踪其在不同年份的发展。
同时,数据中设置了多个虚拟变量来反映公司的特殊情况,如 ST 或 PT 为 1,否则为 0,这可以帮助我们识别那些处于特殊状态的上市公司,分析其创新和研发投入在特殊情况下的变化。金融业为 1,否则为 0,总负债大于总资产为 1,否则为 0 等变量,有助于我们从行业特征和财务健康状况的角度,深入探讨对创新和研发投入的影响。
在地域和行业分类方面,有东部地区为 1,否则为 0、西部地区为 1,否则为 0、中部地区为 1,否则为 0 等地域标识,以及行业名称、行业代码、制造业取两位代码,其他行业用大类等行业分类信息。这些数据能够让我们研究不同地区和行业的上市公司在创新和研发投入上的差异,探寻地域和行业因素对企业创新的影响机制。
在研发投入的具体量化方面,研发投入金额自然对数值、研发人员数量、研发人员数量占比 (%)、研发投入金额等指标,从不同维度详细描述了企业研发投入的规模和结构。而经缺失值填充后的相关指标,则进一步提高了数据的完整性和可用性,为精确的数据分析提供了保障。
此外,数据中还设置了高科技行业为 1,否则为 0、重污染行业为 1,否则为 0 等多个行业特征变量,方便我们聚焦特定类型的行业,研究其在创新和研发投入方面的特点和规律。
这份数据为研究上市公司的创新和研发投入提供了全面、详细且具有深度的信息基础。无论是学术研究人员开展企业创新理论研究,还是投资者评估上市公司的创新能力和发展潜力,亦或是企业管理者借鉴同行的创新投入策略,都能从这份数据中获取有价值的信息。我们期待这份数据能够为相关领域的研究和实践带来新的启发和突破。
注:本文中的数据和指标仅为示例,实际数据请参考最新发布的上市公司-创新投入、研发投入数据(2007-2022)
数据概览

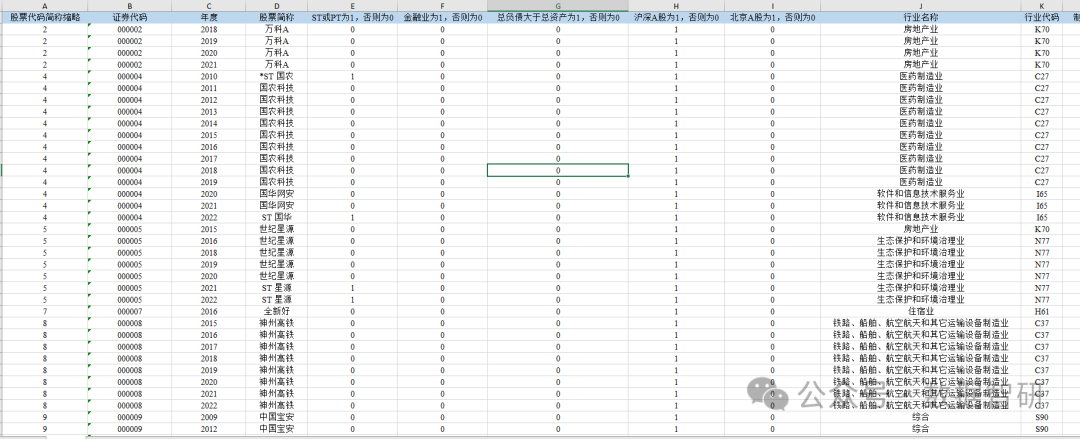
数据跨度:上市公司-创新投入、研发投入数据(2007-2022)
数据说明
1、数据来源网络收集
2、本资源仅用作为学习用途,不能用于商业通途
3、数据整理不易,链接在推文发出后72小时内有效。过期请联系小编付费获取。数据获取方式
数据获取方式
点击关注后台咨询
