机器学习——DBSCAN 聚类算法 + 标准化
DBSCAN 聚类算法详解与实战
1. DBSCAN 简介
DBSCAN(Density-Based Spatial Clustering of Applications with Noise)是一种基于密度的聚类算法,由 Martin Ester 等人在 1996 年提出。
它通过考察数据点的密度分布,将密度相连的点划为同一类,并能自动识别噪声点(离群点)。
与 K-Means 不同,DBSCAN 不需要提前指定簇的数量,而是通过两个核心参数来决定聚类结果:
eps(ε 邻域半径)
min_samples(核心点的最小邻居数)
2. 基本原理
2.1 三类点
在 DBSCAN 中,每个点会被分类为:
核心点(Core Point)
在半径eps内,邻居数(包含自身)不少于min_samples的点。边界点(Border Point)
自身邻居数少于min_samples,但在某个核心点的eps范围内。噪声点(Noise Point / Outlier)
既不是核心点,也不是边界点。
2.2 聚类过程
随机选择一个尚未访问的点。
如果该点是核心点,将其邻居全部纳入同一簇,并递归扩展。
如果该点是边界点,则只将其标记为该簇成员,不扩展。
如果该点是噪声点,标记为噪声(不属于任何簇)。
重复直到所有点都被访问。
3. DBSCAN 常用参数说明(sklearn.cluster.DBSCAN)
| 参数 | 类型 | 默认值 | 作用 | 取值建议 / 说明 |
|---|---|---|---|---|
eps | float | 0.5 | 邻域半径:一个点被视为邻居的最大距离。 | 通过 K 距离图(k-distance graph)寻找“拐点”确定。数值大 → 簇变少;数值小 → 簇变多。 |
min_samples | int | 5 | 核心点最少邻居数(包含自身)。 | 一般取 2 × 数据维度 到 4 × 数据维度。值大 → 更严格,更多噪声点;值小 → 更宽松,簇更大。 |
metric | str 或 callable | "euclidean" | 距离度量方式。 | 常用 "euclidean"(欧氏)、"manhattan"、"cosine" 等。也可自定义函数。 |
metric_params | dict | None | 给 metric 传递的额外参数。 | 例如设置 p=1 或 p=2(闵可夫斯基距离的参数)。 |
algorithm | {'auto','ball_tree','kd_tree','brute'} | "auto" | 邻居搜索算法。 | "ball_tree" 和 "kd_tree" 适合低维;"brute" 用暴力搜索。 |
leaf_size | int | 30 | 构建树结构时的叶子节点大小。 | 一般不用调,影响查询速度而不是聚类效果。 |
p | float | 2 | 闵可夫斯基距离参数。 | p=2 → 欧氏距离;p=1 → 曼哈顿距离。 |
n_jobs | int | None | 并行计算的 CPU 核心数。 | -1 表示使用所有核心,加速计算。 |
最关键的两个参数
eps:控制邻域大小 → 决定簇的规模。min_samples:控制核心点密度阈值 → 决定哪些点能扩展簇。
常见调参思路:
用 K 距离图 找
eps的拐点。根据数据维度 & 噪声情况调整
min_samples。
4. DBSCAN 的优缺点
优点
不需要指定簇数量(相比 K-Means)。
可发现任意形状的簇。
对噪声点具有较强的鲁棒性。
缺点
对 eps 和 min_samples 参数敏感。
高维数据时效果可能不好(“维度灾难”)。
当密度差异很大时,可能不能很好区分簇。
5. Python 实战
我们用一个二维示例数据演示 DBSCAN 聚类。
import matplotlib.pyplot as plt
from sklearn.datasets import make_moons
from sklearn.cluster import DBSCAN# 1. 生成数据
X, y_true = make_moons(n_samples=300, noise=0.05, random_state=42)# 2. 创建 DBSCAN 模型
dbscan = DBSCAN(eps=0.2, min_samples=5)# 3. 训练模型
y_pred = dbscan.fit_predict(X)# 4. 可视化聚类结果
plt.figure(figsize=(6, 6))
plt.scatter(X[:, 0], X[:, 1], c=y_pred, cmap='viridis', s=30)
plt.title("DBSCAN Clustering Result")
plt.show()# 查看标签
print(set(y_pred)) # -1 表示噪声点
代码说明:
make_moons:生成两个半环形数据。eps=0.2:邻域半径 0.2。min_samples=5:核心点邻居至少 5 个。输出标签中
-1表示噪声点。
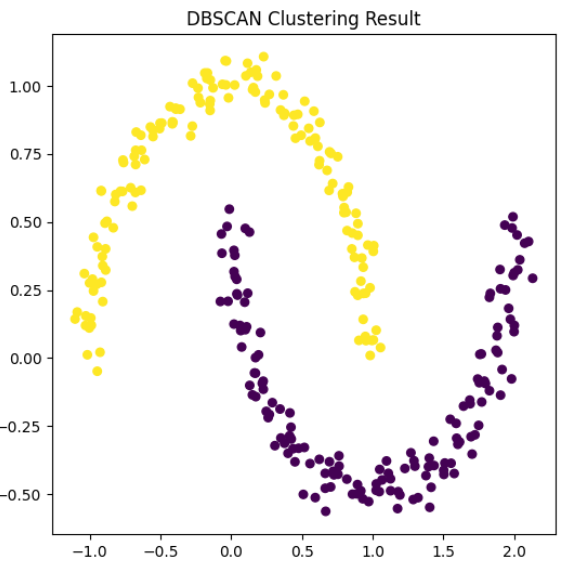
结果:密度相连的点划为同一类
![]()
这个输出结果 {0, 1} 表示:
最终聚类得到了 两个簇(标签 0 和 1)。
没有
-1,说明在这个参数组合下 没有噪声点。
6. 调参技巧
6.1 使用 K 距离图选择 eps
from sklearn.neighbors import NearestNeighborsneighbors = NearestNeighbors(n_neighbors=5)
neighbors_fit = neighbors.fit(X)
distances, indices = neighbors_fit.kneighbors(X)distances = np.sort(distances[:, 4])
plt.plot(distances)
plt.title("K-distance Graph (拐点即 eps 参考值)")
plt.show()
拐点处的值可作为 eps 参考。
DBSCAN 在很多情况下需要 标准化(standardization)或归一化(normalization)


1. DBSCAN 对距离敏感
DBSCAN 是基于距离的聚类算法(默认欧氏距离),核心参数 eps 就是“距离半径”。
如果数据各个特征的数值范围差别很大,距离计算就会被数值范围大的特征主导。
例子:
假设数据有两个特征:
特征 A(身高,单位 cm):范围 150–190
特征 B(体重,单位 kg):范围 40–90
欧氏距离计算时,体重(40–90)变化范围小,身高(150–190)变化范围大,就会让身高差异主导聚类,体重几乎不起作用。
2. eps 的选取依赖尺度一致性
eps 是固定数值的半径,如果特征尺度差异大,就很难找到一个合适的 eps 同时适配所有维度。
标准化后,每个特征的均值为 0,方差为 1,各特征的单位统一到可比较的水平,使得 eps 有更明确的含义。
3. 避免稀疏方向的误判
在高维空间中,如果某些特征范围特别大,会把点之间的距离拉远,导致原本密集的簇被错误地认为是稀疏的,从而被判为噪声点(-1 标签)。
标准化可以缓解这种现象。
4. 代码示例
from sklearn.preprocessing import StandardScaler
from sklearn.datasets import make_blobs
from sklearn.cluster import DBSCAN# 生成数据
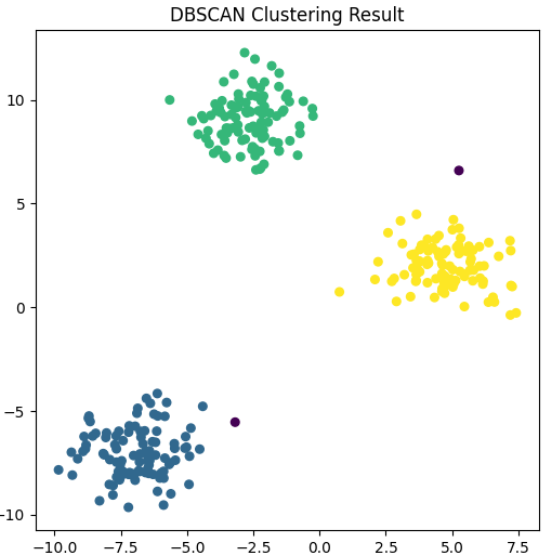
X, _ = make_blobs(n_samples=300, centers=3, cluster_std=1.2, random_state=42)# 不标准化直接聚类
y_pred_raw = DBSCAN(eps=1.5, min_samples=5).fit_predict(X)# 标准化
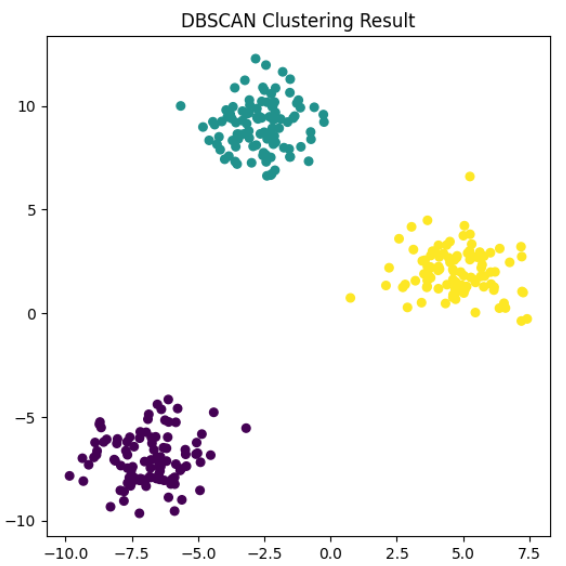
X_scaled = StandardScaler().fit_transform(X)
y_pred_scaled = DBSCAN(eps=0.5, min_samples=5).fit_predict(X_scaled)print("不标准化标签:", set(y_pred_raw))
print("标准化后标签:", set(y_pred_scaled))import matplotlib.pyplot as plt
plt.figure(figsize=(6, 6))
plt.scatter(X[:, 0], X[:, 1], c=y_pred_raw, cmap='viridis', s=30)
plt.title("DBSCAN Clustering Result")
plt.show()plt.figure(figsize=(6, 6))
plt.scatter(X[:, 0], X[:, 1], c=y_pred_scaled, cmap='viridis', s=30)
plt.title("DBSCAN Clustering Result")
plt.show()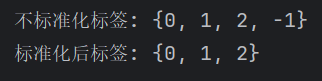
总结
DBSCAN 通过密度定义聚类,不依赖预设簇数。
两个核心参数
eps和min_samples决定效果。适合低维、密度较均匀的数据。
可结合 K 距离图进行参数选择。
DBSCAN 依赖距离计算 → 特征量纲不同会造成偏差。
标准化让每个特征在聚类中权重均等。
一般建议在 特征量纲不同 或 范围差异明显 时进行标准化(
StandardScaler或MinMaxScaler)。
