当前位置： 首页 > web >正文

【递归、搜索与回溯算法】深度优先搜索

web 2025/8/11 7:14:46

在这里插入图片描述

  • 深度优先遍历 VS 深度优先搜索
  • 一、[计算布尔二叉树的值](https://leetcode.cn/problems/evaluate-boolean-binary-tree/description/)
  • 二、[求根节点到叶节点数字之和](https://leetcode.cn/problems/sum-root-to-leaf-numbers/description/)
  • 三、[二叉树剪枝](https://leetcode.cn/problems/binary-tree-pruning/description/)
  • 四、[验证二叉搜索树](https://leetcode.cn/problems/validate-binary-search-tree/description/)
  • 五、[二叉搜索树中第 K 小的元素](https://leetcode.cn/problems/kth-smallest-element-in-a-bst/description/)
  • 六、[二叉树的所有路径](https://leetcode.cn/problems/binary-tree-paths/description/)
  • 结尾

深度优先遍历 VS 深度优先搜索

  • 深度优先遍历：按照深度优先的顺序访问结构中的所有节点
  • 深度优先搜索：在一个状态空间（如迷宫、图、决策树）中寻找满足特定条件的解，可能不需要遍历所有节点，找到解后可提前终止。

遍历是形式，搜索是目的。

  • 遍历强调 “按规则走一遍”，深度优先遍历规定了 “先深入一条路，再回溯” 的访问顺序。这种形式是中性的，本身不带有明确的目标，只是确保覆盖所有元素
  • 搜索则是 “带着目的去遍历”，比如在图中找两个节点的路径、在树中找某个值的节点、在迷宫中找出口 —— 本质上是利用遍历的形式，在访问元素的过程中判断是否满足目标条件，一旦找到就可以停止（或继续寻找所有解）

一、计算布尔二叉树的值

题目描述：
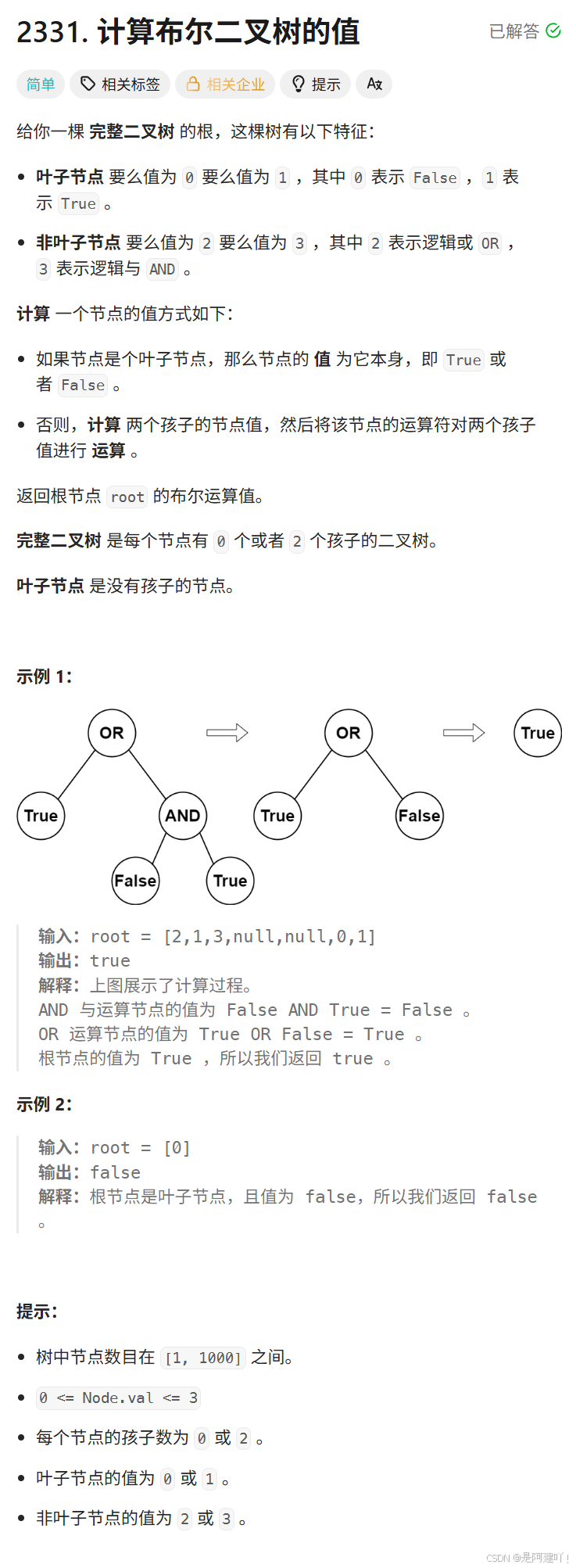
在这里插入图片描述

思路讲解：
本道题需要我们计算布尔二叉树的值，那么首先我们就要计算根节点的左子树的布尔值和右子树的布尔值，而左右子树的布尔值又需要根据它们的左右子树的布尔值计算得来，所以本道题可以使用递归来实现。
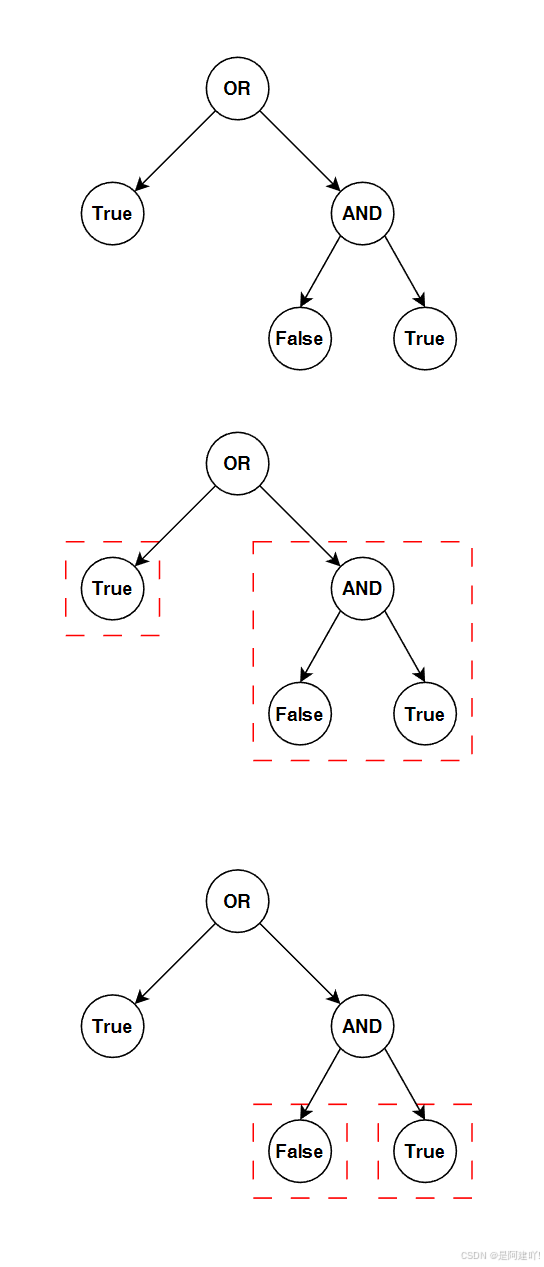
在这里插入图片描述
以下是具体思路：

  • 终止条件：
    • 若当前节点是叶子节点（没有左右孩子），直接返回其值（True 对应 1，False 对应 0）
  • 递归逻辑：
    • 对于非叶子节点，先递归计算左子树的值（left_val）和右子树的值（right_val）
    • 根据当前节点的运算符（2 表示 OR，3 表示 AND），对 left_val 和 right_val 进行逻辑运算：
      • 若节点值为 2（OR）：结果为 left_val OR right_val
      • 若节点值为 3（AND）：结果为 left_val AND right_val
  • 返回结果：
    • 返回当前节点的运算结果，供上层节点使用

编写代码：

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:bool evaluateTree(TreeNode* root) {if(root->left == nullptr && root->right == nullptr)return root->val;bool left = evaluateTree(root->left);bool right = evaluateTree(root->right);return root->val == 2 ? left | right : left & right;}
};

二、求根节点到叶节点数字之和

题目描述：
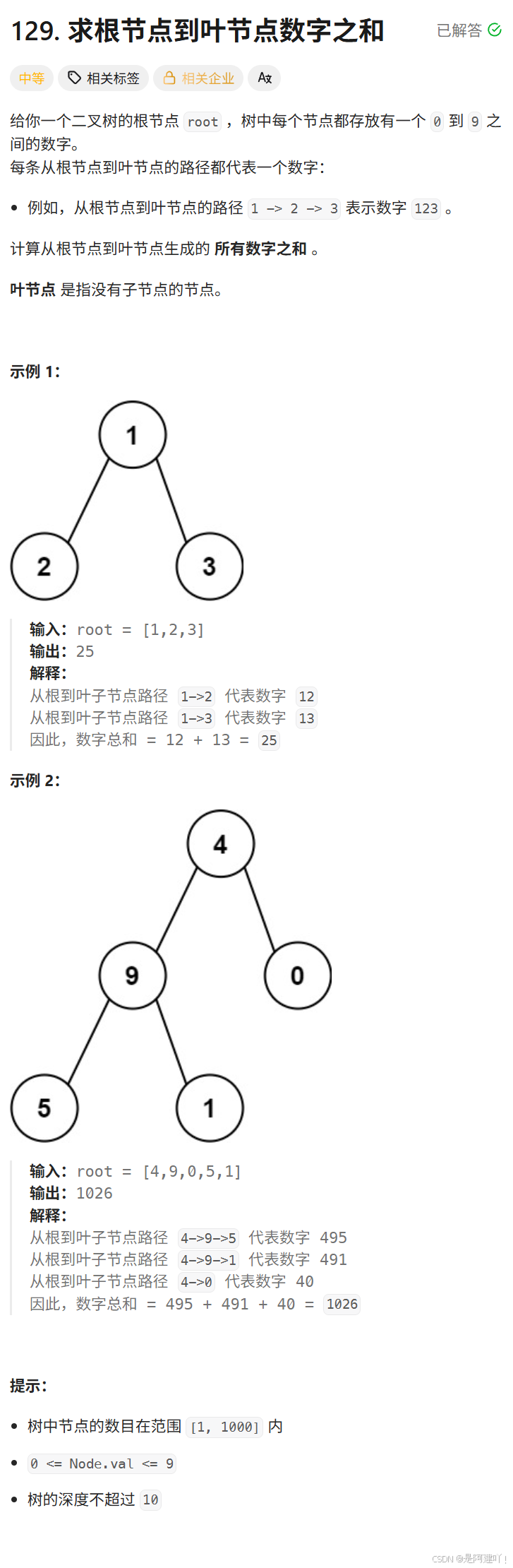
在这里插入图片描述

思路讲解：
本道题需要我们求根节点到叶节点数字之和，那么就需要记录根节点到当前节点形成的数字，通过将数字传递给左右子树，让左右子树形成新的数字，再让左右子树将数字传递给它们的左右子树，直到到了叶子节点，将形成的数字返回，通过层层递归将左右子树返回的值相加即可完成本道题。

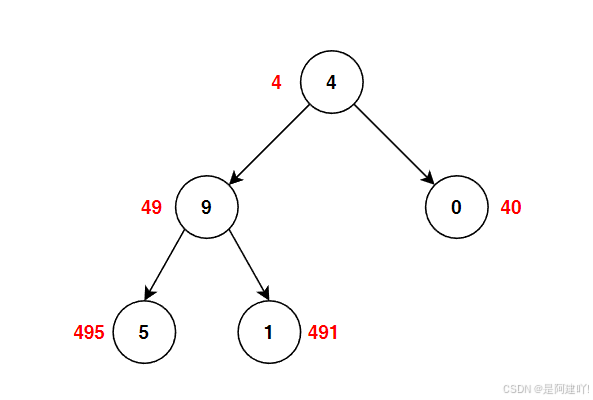
在这里插入图片描述
以下是具体思路：

  • 递归参数：
    • 除了当前节点，还需要一个参数 prveSum 记录从根节点到当前节点的路径所形成的数字
  • 终止条件：
    • 当遇到叶节点时，计算从根节点到当前节点的路径所形成的数字 currentSum ，并返回该值
  • 递归逻辑：
    • 对于非叶节点，更新 currentSum：currentSum = prveSum * 10 + 当前节点值
    • 递归遍历左子树和右子树，将左右子树的返回值相加后返回

编写代码：

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:int _sumNumbers(TreeNode* root , int prevSum) {int curSum = prevSum * 10 + root->val;if(root->left == nullptr && root->right == nullptr)return curSum;int left = 0 , right = 0;if(root->left)left = _sumNumbers(root->left , curSum);if(root->right)right = _sumNumbers(root->right , curSum);return left + right;}int sumNumbers(TreeNode* root) {return _sumNumbers(root,0);}
};

三、二叉树剪枝

题目描述：
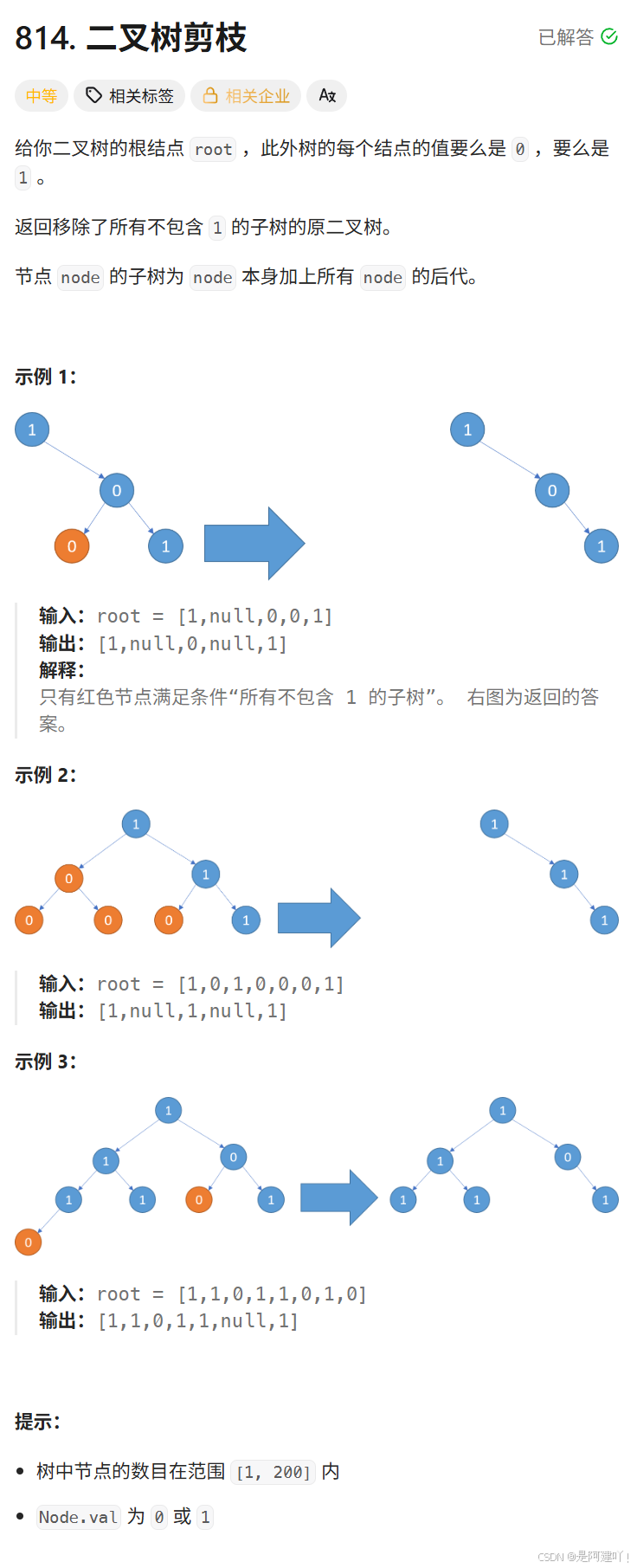
在这里插入图片描述

思路讲解：
本道题需要我们移除了所有不包含 1 的子树，所以我们需要先判断左右子树是否可以被剪枝，左右子树也需要先判断它们的左右子树是否被剪枝，所以可以使用递归的思路完成本道题，以下是具体思路：

  • 终止条件：
    • 若当前节点为空，直接返回空
  • 递归逻辑：
    • 先递归剪枝左子树和右子树，得到修剪后的左、右子树新节点
  • 判断当前子树是否保留：
    • 若当前节点值为 0，且修剪后的左、右子树均为空（说明整个子树没有 1），则移除当前子树，返回空
    • 否则，保留当前节点，将其左、右指针指向修剪后的子树，返回当前节点

编写代码：

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:TreeNode* pruneTree(TreeNode* root) {if(root == nullptr) return nullptr;root->left = pruneTree(root->left);root->right = pruneTree(root->right);return root->left == nullptr && root->right == nullptr && root->val == 0 ? nullptr : root;}
};

四、验证二叉搜索树

题目描述：
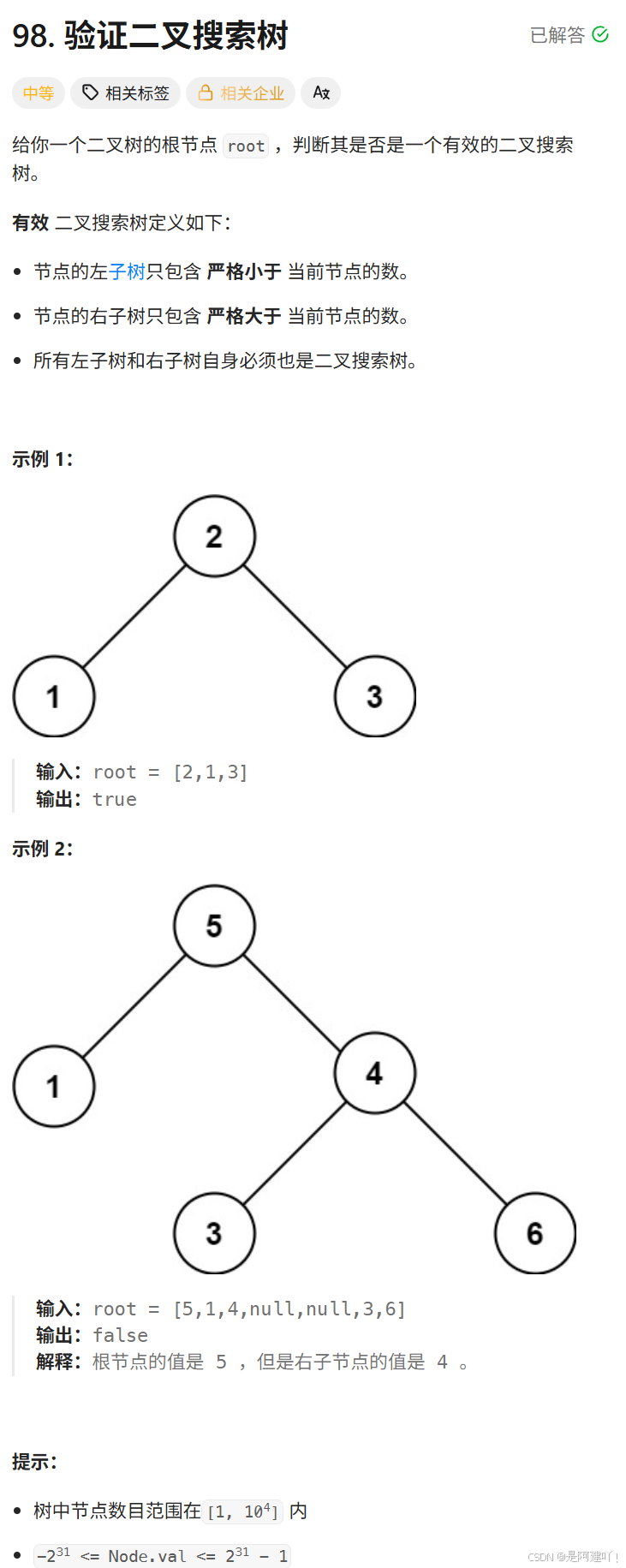
在这里插入图片描述

思路讲解：
本道题需要我们验证二叉树是否为二叉搜索树，这里就可以利用二叉搜索树的特性，也就是二叉树的中序遍历是有序的，来判断是否为二叉搜索树，以下是具体思路：

  • 核心逻辑：
    • 二叉搜索树的中序遍历结果是严格递增的序列。若遍历结果中出现非递增情况（如后一个元素 <= 前一个元素），则不是有效的二叉搜索树
  • 状态记录：
    • 用一个变量记录上一个访问的节点值
  • 递归逻辑：
    • 中序遍历左子树，过程中检查是否已出现非递增情况，出现说明该子树不是搜索二叉树，返回 false
    • 访问当前节点，与前一个访问的节点值比较：若当前节点值 ≤ 前一个节点值，说明该子树不是搜索二叉树，返回 false
    • 中序遍历右子树，同样传递比较状态

编写代码：

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {long long prev = LLONG_MIN;
public:bool isValidBST(TreeNode* root) {if(root == nullptr) return true;bool left = isValidBST(root->left);if(!left || root->val <= prev) return false;prev = root->val;return isValidBST(root->right);}
};

五、二叉搜索树中第 K 小的元素

题目描述：
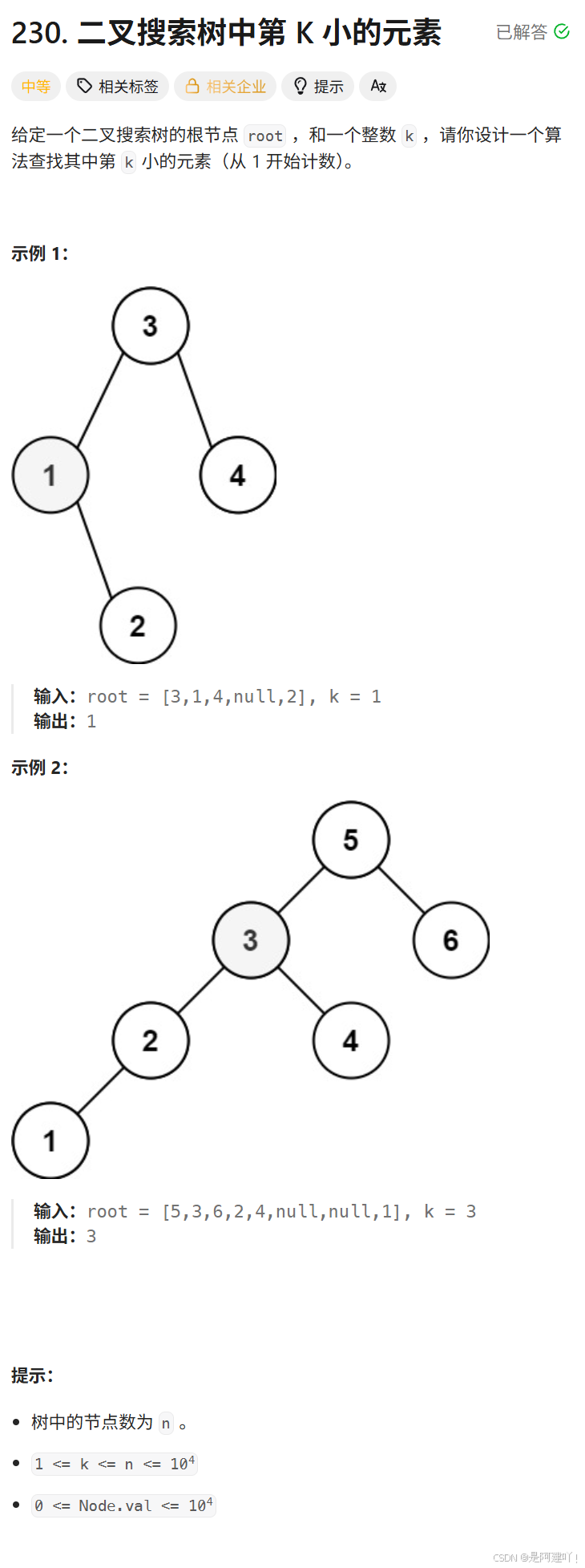
在这里插入图片描述

思路讲解：
本道题需要我们找到二叉搜索树中第 K 小的元素，依旧是利用二叉搜索树中序遍历是有序的特性，找到第K小的元素。以下是具体思路：

  • 核心逻辑：
    • 二叉搜索树的中序遍历会得到一个递增序列，第 k 个被访问的节点就是第 k 小的元素
  • 递归逻辑：
    • 中序遍历左子树，过程中减少还需要访问的节点数量
    • 若已找到第 k 个节点，直接返回结果
    • 访问当前节点，将计数减1 ；若计数等于 0，当前节点即为目标，返回其值
    • 中序遍历右子树，过程中减少还需要访问的节点数量
  • 终止条件：
    • 当计数为 0 时，终止遍历并返回对应节点值

编写代码：

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {int cnt , ans;
public:void _kthSmallest(TreeNode* root) {if(root == nullptr || cnt == 0) return;_kthSmallest(root->left);cnt--;if(cnt == 0) ans = root->val;_kthSmallest(root->right);}int kthSmallest(TreeNode* root, int k) {cnt = k;_kthSmallest(root);return ans;}
};

六、二叉树的所有路径

题目描述：
***

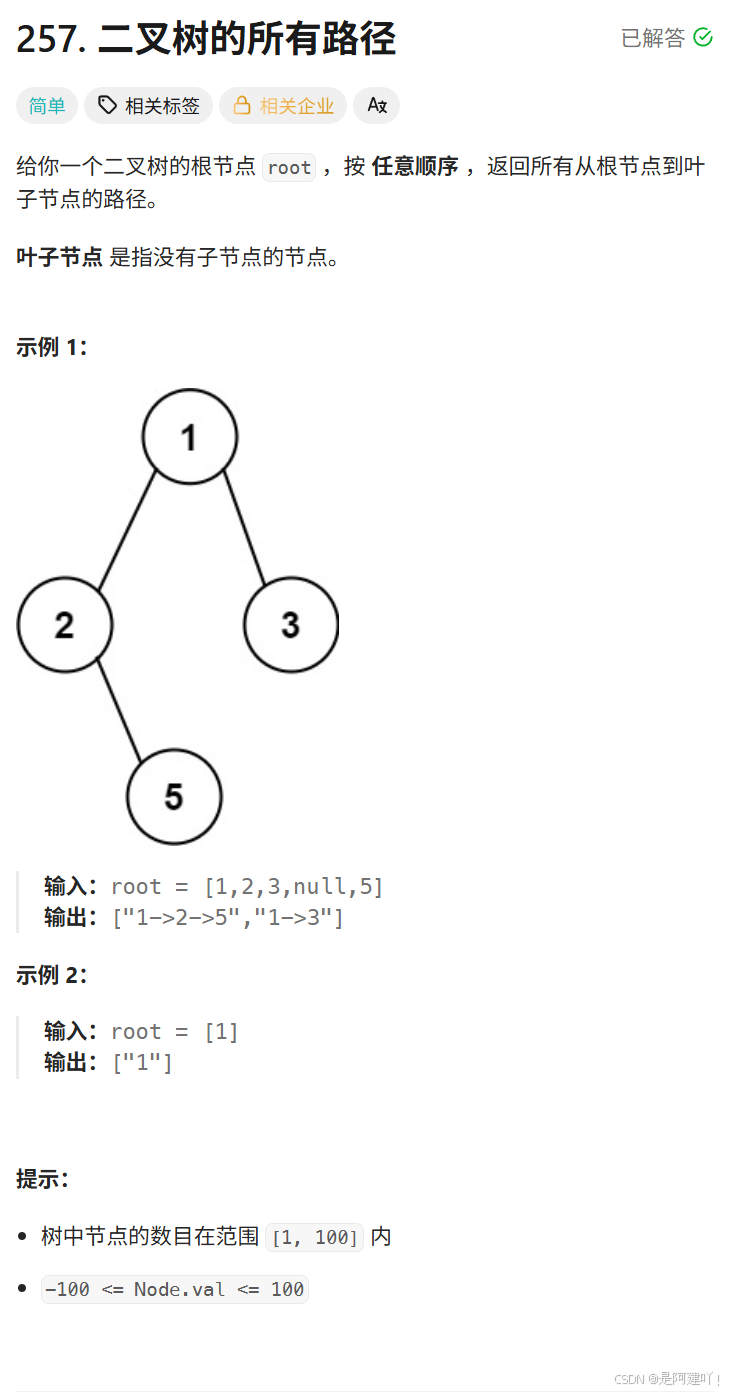
思路讲解：
本道题需要我们找出二叉树的所有路径，也就是我们需要遍历一遍二叉树，并且记录当前路径，当遍历到叶子节点的时候，将当前路径加入到结果集中，以下是具体思路：

  • 函数参数：
    • 当前节点，也就是子树的根节点
    • 记录从根节点到当前节点的路径
  • 终止条件：
    • 当遇到叶子节点时，将当前路径加入完整路径的结果集并返回
  • 递归逻辑：
    • 若当前节点不是叶子节点，更新当前路径：拼接当前节点值和 “->”
    • 递归遍历左子树，传递更新后的当前路径
    • 递归遍历右子树，传递更新后的当前路径

编写代码：

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {vector<string> ans;
public:void _binaryTreePaths(TreeNode* root , string path){path += to_string(root->val);if(root->left == nullptr && root->right == nullptr){ans.push_back(path);return;}path += "->";if(root->left) _binaryTreePaths(root->left , path);if(root->right) _binaryTreePaths(root->right , path); }vector<string> binaryTreePaths(TreeNode* root) {_binaryTreePaths(root,string());return ans;}
};

结尾

如果有什么建议和疑问，或是有什么错误，大家可以在评论区中提出。
希望大家以后也能和我一起进步！！🌹🌹
如果这篇文章对你有用的话，希望大家给一个三连支持一下！！🌹🌹
在这里插入图片描述

http://www.xdnf.cn/news/17577.html

相关文章：

  • Spring AOP 底层实现（面试重点难点）
  • 结构化记忆、知识图谱与动态遗忘机制在医疗AI中的应用探析(上)
  • scikit-learn/sklearn学习|线性回归解读
  • 深度相机---双目深度相机
  • 神经机器翻译（NMT）框架：编码器-解码器（Encoder-Decoder）结构详解
  • tlias智能学习辅助系统--原理篇-SpringBoot原理-自动配置-自定义starter
  • Agent在游戏行业的应用：NPC智能化与游戏体验提升
  • SupChains团队：化学品制造商 ChampionX 供应链需求预测案例分享（十七）
  • Word XML 批注范围克隆处理器
  • 【从汇编语言到C语言编辑器入门笔记9】 - 链接器的执行过程
  • Docker部署到实战
  • K8s四层负载均衡-service
  • Python爬虫实战：研究BlackWidow,构建最新科技资讯采集系统
  • 【话题讨论】GPT-5 发布全解读：参数升级、长上下文与多领域能力提升
  • log4cpp、log4cplus 与 log4cxx 三大 C++ 日志框架
  • MPLS对LSP连通性的检测
  • 力扣559:N叉树的最大深度
  • 【力扣198】打家劫舍
  • Ubuntu 24.04 适配联发科 mt7902 pcie wifi 网卡驱动实践
  • 联邦学习之------VT合谋
  • 计算机网络：路由聚合的注意事项有哪些？
  • 【嵌入式】Linux的常用操作命令(2)
  • 米哈游笔试——求强势顶点的个数
  • [概率 DP]808. 分汤
  • 第4章 程序段的反复执行2 while语句P128练习题（题及答案）
  • pytorch llm 计算flops和参数量
  • Gltf 模型 加载到 Cesium 的坐标轴映射浅谈
  • 深入理解C++构造函数与初始化列表
  • Python训练营打卡Day27-类的定义和方法
  • AudioLLM