深度相机---双目深度相机

双目深度相机是一种通过模拟人类双眼视觉机制，利用立体视觉原理计算场景三维深度信息的设备。其核心价值在于以较低成本实现非接触式深度感知，广泛应用于机器人导航、AR/VR交互、工业检测、自动驾驶等领域。相比结构光、TOF等其他深度感知技术，双目相机在强光环境适应性、中等距离精度等方面具有独特优势，但也面临依赖场景纹理、计算复杂度高等问题。

一、核心原理：立体视觉与三角测量的数学本质

双目深度相机的底层逻辑源于“三角测量”（Triangulation），即通过两个已知位置的观测点（左右摄像头）与空间目标点构成三角形，利用几何关系反推目标点的三维坐标。这一过程的核心是“视差”（Disparity）的计算，而视差与深度的映射关系则依赖于相机的内外参数校准。

1. 视差：双目相机感知的核心

人类双眼观察同一物体时，左眼与右眼看到的图像存在水平方向的偏移，这种偏移即为“视差”。视差的大小与物体距离直接相关：近处物体视差大，远处物体视差小（极端情况下，无穷远处物体的视差趋近于0）。

在双目相机中，视差被定义为“空间中同一点在左、右图像中投影的水平像素坐标差值”。假设左相机中某点像素坐标为$(x_l,y_l)$，右相机中对应点坐标为$(x_r,y_r)$，由于经过极线校正（后文详述），左右图像的对应点在同一水平线上（即$y_l=y_r$），因此视差可简化为：
$$d=x_L-x_R$$
（$d$为视差，单位为像素；$d>0$表示左图中该点在右图对应点右侧）

2. 三角测量公式：从视差到深度的映射

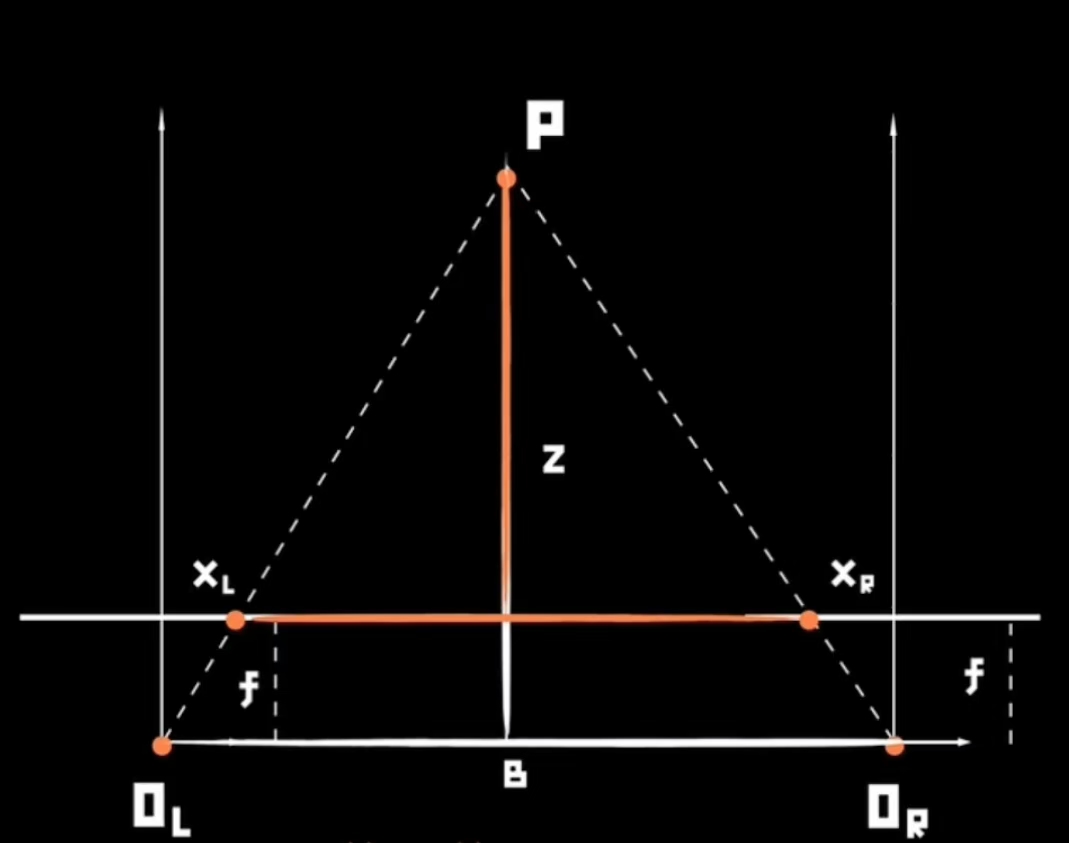
深度计算的几何基础是“基线-焦距-视差”三角关系。如图所示（示意图），左右相机光心分别为$O_L$和$O_R$，两者之间的距离为基线$B$（单位：mm）；两相机焦距均为$f$（单位：mm，镜头到成像平面的距离）；空间点$P$在左、右成像平面上的投影分别为$X_l$和$X_r$，对应像素坐标的水平差值为视差$d$（单位：像素）。

根据相似三角形原理（$△O_L{O}_{R}P\sim △P_l{P}_{r}P$），可推导出空间点$P$到相机平面的深度$z$（单位：mm）为：
$$z=\frac{B\cdot f}{d}$$

公式解读：

• 深度$Z$与基线$B$、焦距$f$成正比：基线越长、焦距越大，相同视差下的深度测量越精确（尤其适合远距离场景）。
• 深度$Z$与视差$d$成反比：视差越小（物体越远），深度计算对$d$的误差越敏感（例如，$d=1$像素时，$d$的±1像素误差会导致$Z$的±100%误差）。

3. 极线几何：简化匹配的数学基础

极线和极平面参考OpenCV的这篇文档

未经校正的双目图像中，空间点在左右图像中的投影可能分布在不同水平线上，导致对应点搜索需遍历全图像，计算量极大。“极线几何”（Epipolar Geometry）通过定义“极线”（Epipolar Line）解决这一问题：空间点在左图中的投影点，其在右图中的对应点必定落在一条特定的直线（极线）上。 （极线约束定理）

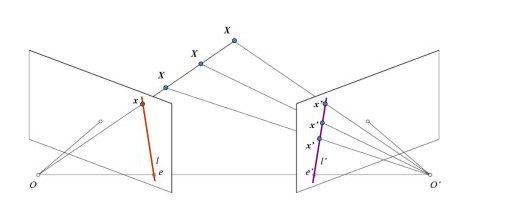
极线几何的核心参数包括：

• 极点（Epipole）：左相机光心$O_l$在右图上的投影为右极点$e_r$，右相机光心$O_r$在左图上的投影为左极点$e_l$。
• 极平面（Epipolar Plane）：由$O_l$、$O_r$和空间点$P$构成的平面，与左右成像平面的交线即为极线。

通过相机标定获取内参（焦距、主点、畸变系数）和外参（旋转矩阵$R$、平移向量$T$）后，可通过“极线校正”将左右图像的极线调整为水平且共线（即同一行），此时对应点搜索仅需在同一水平线上进行，计算量降低90%以上。

二、硬件结构

双目相机的硬件设计需满足“空间同步”（基线固定）和“时间同步”（曝光同步）两大核心要求，否则会直接破坏视差计算的几何基础。其硬件结构可分为五大核心模块，各模块的精度与协同性决定了最终深度图的质量。

1. 双摄像头模组：视觉感知的“双眼”

双摄像头是图像采集的核心，其参数一致性和空间排布直接影响深度精度：

• 参数一致性：左右相机需严格匹配焦距（误差需<1%）、分辨率（如1280×720、2560×1440）、像元尺寸（如3.0μm×3.0μm）、畸变特性（径向畸变<1%，切向畸变<0.5%）。参数不匹配会导致校正后极线仍存在偏差，增加匹配难度。
• 空间排布：通常采用水平平行排布（基线方向为X轴），基线长度$B$根据应用场景设计：近距离场景（如AR手势交互）用短基线（5-15cm），中远距离场景（如机器人导航）用长基线（20-50cm）。基线偏差（如垂直方向倾斜>0.1°）会引入额外视差误差，需通过机械结构（如精密导轨）保证平行度。
• 传感器类型：主流采用CMOS传感器（相比CCD成本低、帧率高），需支持全局快门（Global Shutter）——避免滚动快门（Rolling Shutter）导致的动态场景图像扭曲（如快速移动的物体在左右图中形状错位）。

2. 同步控制模块：时间一致性的“保障”

左右相机必须在同一时刻曝光，否则动态场景中物体的运动会导致视差计算错误（例如，汽车行驶中，不同步的左右图像会使同一车辆在两图中位置偏移，产生虚假视差）。同步方式分为：

• 硬件同步：通过触发信号（如GPIO脉冲）强制左右相机同时开启曝光，同步误差可控制在<10μs，适合高速动态场景（如自动驾驶）。
• 软件同步：通过系统时钟校准曝光时刻，同步误差通常>1ms，仅适合静态场景（如工业检测）。

3. 镜头模组：成像质量的“窗口”

镜头的光学性能直接影响图像清晰度和纹理保留，进而影响立体匹配精度：

• 焦距与视场角：短焦距（如8mm）适合广角场景（视场角>90°），但远距离视差小、精度低；长焦距（如25mm）视场角窄（<30°），但远距离视差更明显，适合长焦场景。
• 畸变控制：鱼眼镜头畸变率高（>10%），需通过算法校正；工业级镜头畸变率可控制在<1%，减少校正负担。
• 光圈与曝光：大光圈（如F/1.8）适合弱光环境，但景深小（易导致前后景失焦）；小光圈（如F/4.0）景深大，但进光量少，需提高ISO（可能引入噪声）。

4. 校准模块：参数精度的“基准”

出厂前需通过“相机标定”获取内参和外参，这是后续图像校正和深度计算的前提。标定流程基于张正友标定法：

1. 用双目相机拍摄不同姿态的棋盘格标定板（至少10组图像）；
2. 通过角点检测计算棋盘格在图像中的像素坐标，结合已知的物理尺寸（如棋盘格方格边长20mm），反推内参（内参矩阵$K=\left[\begin{array}{ccc}{f}_x& 0& c_x\\ 0& f_y& c_y\\ 0& 0& 1\end{array}\right]$，其中$f_x=f/dx$、$f_y=f/dy$为像素焦距，$c_x,c_y$为主点坐标，$dx,dy$为像元尺寸）和外参（旋转矩阵$R$、平移向量$T$）；
3. 计算畸变系数（径向畸变$k_1,k_2,k_3$和切向畸变$p_1,p_2$），用于校正镜头畸变。

标定精度要求：内参误差<0.5%，外参旋转角误差<0.1°，平移向量（基线）误差<0.1mm，否则会导致深度计算误差随距离呈线性放大（例如，基线误差1mm，在10m距离处深度误差可达0.1m）。

5. 计算与传输模块：深度输出的“引擎”

立体匹配算法计算量大（如1280×720分辨率图像，SGBM算法单次匹配需10^8次运算），需专用硬件加速：

• FPGA：适合并行处理（如块匹配中的窗口计算），延迟低（<10ms），但开发难度高；
• ASIC：定制化电路（如Intel Movidius Myriad X），功耗低（<5W），适合嵌入式设备；
• GPU：适合深度学习匹配算法（如PSMNet），通过CUDA并行加速，精度高但功耗大（>20W）。

传输接口需满足高带宽需求（如1280×720@30fps的RGB图像，单路数据量约80Mbps，双路+深度图需>200Mbps），常用USB3.0（5Gbps）、GMSL（6Gbps）或Ethernet（10Gbps）。

三、工作流程：从图像到深度的全链路解析

双目相机的工作流程可分为“1.图像采集-2.校正-3.匹配-4.深度计算-5.后处理”五大步骤，每一步的精度都会直接影响最终深度图质量。

1. 图像采集：原始数据的获取

左右相机在同步信号触发下，对同一场景进行曝光成像，输出左图$I_l$和右图$I_r$（RAW格式或RGB格式）。需注意：

• 动态场景中，若同步误差>物体运动的像素距离（如车速10m/s，同步误差1ms，物体在图像中偏移约3像素），会导致视差计算错误；
• 弱光环境下，需开启红外补光灯（波长850nm，避免可见光干扰），但补光不均匀会导致图像亮度差异，增加匹配难度。

2. 图像校正：极线对齐的关键一步

未经校正的图像存在畸变和极线倾斜，需通过两步处理将其转换为“理想立体图像对”：

• 畸变校正：利用内参中的畸变系数，对左右图像进行几何修正（如径向畸变校正公式：$x_{corr}=x\cdot (1+k_1{r}^2+k_2{r}^4+k_3{r}^6)+2p_{1}xy+p_2(r^2+2x^2)$，其中$r^2=x^2+y^2$）；
• 极线校正：根据外参$R$和$T$，计算校正矩阵（通过单应性变换$H_l,H_r$），将左右图像映射到同一平面，使极线水平对齐（即$y_l=y_r$）。校正后，对应点搜索范围从全图像压缩到同一行，效率提升10倍以上。
  我们双目相机拍摄的时候实际情况下如下图a,两个图像做匹配时如我们图中蓝色箭头指示的匹配点那样，需要在全图中进行查找。但是如果我们对相机进行校正，使得它们成像面平行且行对齐如下图b，匹配点在同一行。那么我们只需在同行上查找，大大节约时间。因此，极线校正目的是对两幅图像的二维匹配搜索变成一维，节省计算量，排除虚假匹配点。
  

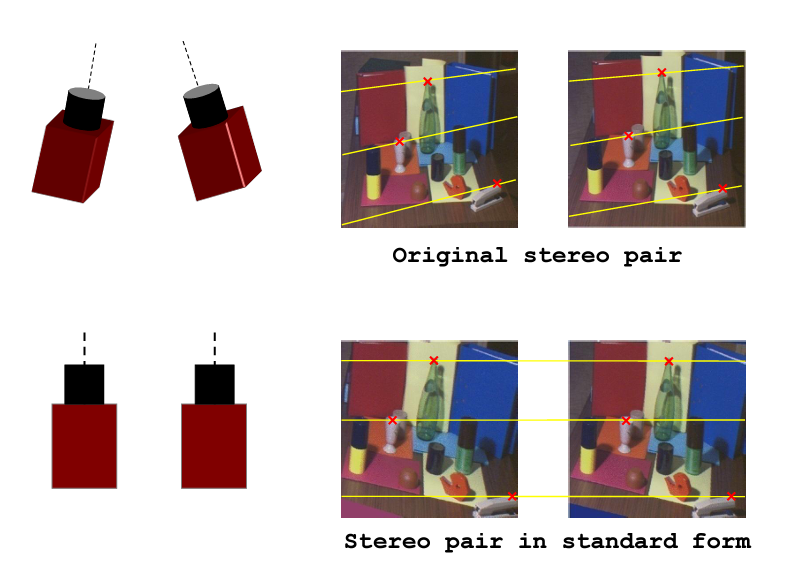
3. 立体匹配：视差计算的核心

立体匹配的目标是为左图每个像素$(x,y)$在右图同一行$y$上找到最相似的像素，得到视差$d$。这是双目相机最复杂的步骤，算法需平衡精度、速度和鲁棒性：

• 传统算法：

  • BM（Block Matching）：以左图像素为中心取$n\times n$窗口（如5×5、9×9），在右图对应行滑动窗口计算相似度（如SSD：$\sum (I_l-I_r{)}^2$），取最小值对应的位置为匹配点。优点是速度快（适合FPGA实现），缺点是弱纹理区域易匹配错误，窗口尺寸需根据场景调整（小窗口适合细节，大窗口抗噪声）。
  • SGBM（Semi-Global Block Matching）：在BM基础上引入全局能量函数（$E=\sum (D(x)+P1\cdot |d(x)-d(x-1)|+P2\cdot \text{large difference})$），通过动态规划在8个方向优化匹配结果，平衡局部匹配的噪声和全局一致性。精度优于BM（误差<3%@5m），但计算量增加3倍。

• 深度学习算法：

  • PSMNet（Pyramid Stereo Matching Network）：通过金字塔特征提取（左图和右图分别提取多尺度特征），构建4D代价体（$H\times W\times D\times C$，$D$为视差范围），用3D卷积进行代价聚合，最后通过softmax输出视差。在弱纹理、遮挡区域表现优于传统算法（误差<2%@5m），但计算量是SGBM的10倍以上，需GPU支持。

4. 深度计算：从视差到三维坐标的转换

根据三角测量公式$Z=\frac{B\cdot f}{d}$，将视差图转换为深度图。需注意单位转换：

• 像素焦距$f_x=f/dx$（$dx$为像元尺寸，单位mm/像素），因此$f=f_x\cdot dx$，代入公式得$Z=\frac{B\cdot f_x\cdot dx}{d}=\frac{B\cdot f_x}{d}\cdot dx$。实际应用中，厂商通常通过标定将$B\cdot f_x\cdot dx$预计算为“尺度因子”，直接用$Z=\text{scale}/d$计算深度（单位m）。

5. 后处理：深度图的优化与修复

原始深度图存在三类问题：匹配错误（噪声）、遮挡/弱纹理导致的空洞、边缘模糊。后处理步骤包括：

• 噪声去除：中值滤波（去除椒盐噪声）、双边滤波（保留边缘的同时平滑噪声）；
• 空洞填充：对遮挡区域（视差超出范围），采用邻域插值（如基于左右一致性检测，用可信区域的深度值填充）；
• 边缘优化：结合原图边缘信息（如Canny边缘检测），对深度图边缘进行锐化，减少物体边缘的深度模糊。

四、精度与鲁棒性的相关问题

1. 立体匹配的鲁棒性困境

匹配错误是深度图误差的主要来源，根源在于场景特性与算法局限：

• 弱纹理区域：如白墙、纯色桌面，图像梯度接近0，不同位置的窗口相似度差异小，易导致随机匹配（例如，白墙区域可能出现深度跳变）。解决方案：引入语义信息（如深度学习算法利用上下文特征），或主动投射纹理图案（混合结构光与双目技术）。
• 重复纹理区域：如砖块墙、格栅，多个位置的窗口特征高度相似，算法难以区分真实对应点（视差误差可能达10像素以上）。解决方案：增加匹配窗口的尺寸（利用全局特征），或结合运动视差（通过多帧图像优化）。
• 遮挡区域：前景物体遮挡背景（如人站在墙前），被遮挡区域在另一幅图像中无对应点，导致深度空洞（占比可达10-20%）。解决方案：基于左右一致性检测（左图视差与右图反投影视差差异>阈值则标记为遮挡），用背景填充或多帧融合修复。
  

2. 校准精度的稳定性难题

相机参数会随环境变化漂移，导致深度精度下降：

• 温度漂移：温度变化10℃，镜头焦距可能变化0.1%（如25mm焦距变为25.025mm），基线因机械结构热胀冷缩变化0.05mm，在10m距离处深度误差可达0.1m。
  解决方案：采用低膨胀系数材料（如殷钢）制作基线结构，或通过在线标定（实时检测棋盘格或自然特征）动态更新参数。
• 振动与冲击：车载、机器人等场景中，振动可能导致左右相机相对姿态变化（如旋转0.5°），极线校正失效，视差计算误差增大。
  解决方案：用刚性结构固定相机（如金属支架），或集成IMU（惯性测量单元），通过运动补偿修正姿态变化。

3. 实时性与精度的平衡矛盾

高分辨率与高精度需求导致计算量爆炸：

• 分辨率与帧率的权衡：1280×720图像的SGBM算法在FPGA上可实现30fps，但升级到2560×1440后帧率降至10fps以下；深度学习算法在GPU上处理1280×720图像需20ms/帧，难以满足实时性（<33ms）。
  解决方案：采用“感兴趣区域（ROI）匹配”（仅对前景目标计算深度），或降采样处理（牺牲边缘精度换取速度）。
• 硬件成本的限制：FPGA/ASIC开发成本高（百万级人民币），中小厂商难以承担；GPU方案功耗大（>20W），无法用于电池供电设备（如手持AR设备）。
  解决方案：探索轻量级深度学习模型（如MobileStereoNet），通过模型压缩降低计算量。

4. 深度范围的固有局限

基线固定导致双目相机的有效深度范围受限：

• 近距离盲区：当物体距离$Z<Z_{\text{min}}=\frac{B\cdot f}{d_{\text{max}}}$（$d_{\text{max}}$为最大可测视差，通常为图像宽度的1/2），视差超出搜索范围，无法匹配。例如，基线10cm、焦距16mm、图像宽度1280像素，$Z_{\text{min}}\approx 0.25m$，更近的物体（如20cm）会成为盲区。
• 远距离精度衰减：当$Z>Z_{\text{max}}=\frac{B\cdot f}{d_{\text{min}}}$（$d_{\text{min}}=1$像素），视差$d=1$像素，此时$d$的±1像素误差会导致$Z$的±100%误差。例如，基线10cm、焦距16mm，$Z_{\text{max}}\approx 16m$，20m处的深度误差可能达±10m。
  解决方案：采用多基线设计（如双基线相机，近距离用短基线，远距离用长基线），通过切换基线或融合多组深度图扩展有效范围，但会增加硬件复杂度和成本。