【Redis#8】Redis 数据结构 -- Zset 类型

一、引言

定义：有序集合（Zset）是Redis中的一种数据结构，它结合了哈希表和跳跃列表的特性。每个 member 都有一个分数(score)，根据这个分数进行排序。

特点：

• member 不能重复，但分数可以相同（理解：一次考试之后，每个人的每个科目都只有一个唯一的分数，但这些不同科目的分数允许相同）
• 通过分数实现有序性。
• 支持范围查询、排名计算等功能。

二、Set 命令

象常用命令如下表(点击命令可查看命令详细说明)。

命令	说明	时间复杂度
BZPOPMAX key [key …] timeout]	从一个或多个排序集中删除并返回得分最高的成员，或阻塞，直到其中一个可用为止	O(log(N))
BZPOPMIN key [key …] timeout]	从一个或多个排序集中删除并返回得分最低的成员，或阻塞，直到其中一个可用为止	O(log(N))
ZADD key [NXXX] [CH] [INCR] score member [score member …]	添加到有序set的一个或多个成员，或更新的分数，如果它已经存在	O(log(N))
ZCARD key	获取一个排序的集合中的成员数量	O(1)
ZCOUNT key min max	返回分数范围内的成员数量	O(log(N))
ZINCRBY key increment member	增量的一名成员在排序设置的评分	O(log(N))
ZINTERSTORE	相交多个排序集，导致排序的设置存储在一个新的关键	O(NK)+O(Mlog(M))
ZLEXCOUNT key min max	返回成员之间的成员数量	O(log(N))
ZPOPMAX key count	删除并返回排序集中得分最高的成员	O(log(N)*M)
ZPOPMIN key count	删除并返回排序集中得分最低的成员	O(log(N)*M)
ZRANGE key start stop WITHSCORES	根据指定的index返回，返回sorted set的成员列表	O(log(N)+M)
ZRANGEBYLEX key min max LIMIT offset count	返回指定成员区间内的成员，按字典正序排列, 分数必须相同。	O(log(N)+M)
ZREVRANGEBYLEX key max min [LIMIT offset count]	返回指定成员区间内的成员，按字典倒序排列, 分数必须相同	O(log(N)+M)
ZRANGEBYSCORE key min max [WITHSCORES]	返回有序集合中指定分数区间内的成员，分数由低到高排序。	O(log(N)+M)
ZRANK key member	确定在排序集合成员的索引	O(log(N))
ZREM key member member […]	从排序的集合中删除一个或多个成员	O(M*log(N))
ZREMRANGEBYLEX key min max	删除名称按字典由低到高排序成员之间所有成员。	O(log(N)+M)
ZREMRANGEBYRANK key start stop	在排序设置的所有成员在给定的索引中删除	O(log(N)+M)
ZREMRANGEBYSCORE key min max	删除一个排序的设置在给定的分数所有成员	O(log(N)+M)
ZREVRANGE key start stop [WITHSCORES]	在排序的设置返回的成员范围，通过索引，下令从分数高到低	O(log(N)+M)
ZREVRANGEBYSCORE key max min [WITHSCORES] [LIMIT offset count]	返回有序集合中指定分数区间内的成员，分数由高到低排序。	O(log(N)+M)
ZREVRANK key member	确定指数在排序集的成员，下令从分数高到低	O(log(N))
ZSCORE key member	获取成员在排序设置相关的比分	O(1)
ZUNIONSTORE	添加多个排序集和导致排序的设置存储在一个新的关键	O(N)+O(M log(M))
ZSCAN key cursor [MATCH pattern] [COUNT count]	迭代sorted sets里面的元素	O(1)

1. 普通命令🧱

1.1 ZADD & ZINCRBY

① ZADD：添加或者更新指定的元素以及关联的分数到zset中，分数应该符合double类型，+inf/-inf作为正负极限也是合法的。

语法：

ZADD key [NX | XX] [GT | LT] [CH] [INCR] score member [score member ...]

ZADD 的相关选项：

• XX：仅仅用于更新已经存在的元素，不会添加新元素。
• NX：仅用于添加新元素，不会更新已经存在的元素。
• LT/GT：这个选项的意思是 less than 和 greater than 的意思，这两个意思表示的是现在如果要进行更新分数，那么如果当前的分数比之前的分数小，就更新成功，否则就不更新，反之同理
• CH：默认情况下，ZADD返回的是本次添加的元素个数，但指定这个选项之后，就会还包含本次更新的元素的个数。
• INCR：此时命令类似ZINCRBY的效果，将元素的分数加上指定的分数。此时只能指定一个元素和分数。

时间复杂度：O(log(N))

对于 zset 来说，时间复杂度就不一样了，在 set 中的各项操作基本都是 O(1) 的时间复杂度，而在 zset 中却被放到了 O(logn)，这是因为毕竟是有序结构，要找到合适的位置才能放，所以这里是 logn，那为什么不是 O(n) 呢？其实更多的是借助了跳表这样的数据结构，可以快速定位到对应的位置，进行元素的插入工作

案例如下：

127.0.0.1:6379> zadd myzset 10 one 20 two
(integer) 2
127.0.0.1:6379> zrange myzset
(error) ERR wrong number of arguments for 'zrange' command
127.0.0.1:6379> zrange myzset 0 -1
1) "one"
2) "two"
127.0.0.1:6379> zrange myzset 0 -1 WITHSCORES
1) "one"
2) "10"
3) "two"
4) "20"
127.0.0.1:6379> zadd myzset CH 100 one
(integer) 1
127.0.0.1:6379> zadd myzset INCR 20 two
"40"127.0.0.1:6379> zrange myzset 0 -1 WITHSCORES
1) "two"
2) "40"
3) "one"
4) "100"

② ZINCRBY：为指定的元素的关联分数添加指定的分数值

语法

ZINCRBY key increment member

1.2 ZCARD & ZCOUNT & ZSCORE

① ZCARD：获取一个zset的基数（cardinality），即zset中的元素个数（语法：ZCARD key

② ZCOUNT：计算分数范围内的元素数量（语法：ZCOUNT key min max

③ ZSCORE：返回指定元素的分数

使用如下

127.0.0.1:6379> ZCARD myzset
(integer) 2
127.0.0.1:6379> zrange myzset 0 -1 WITHSCORES
1) "two"
2) "40"
3) "one"
4) "100"127.0.0.1:6379> ZCOUNT myzset 0 50
(integer) 1
127.0.0.1:6379> ZCOUNT myzset (0 (40 # ( 表示开区间
(integer) 0
127.0.0.1:6379> ZCOUNT myzset -inf inf
(integer) 2127.0.0.1:6379> ZSCORE myzset "one"
"100"

1.3 ZRANGE & ZREVRANGE & ZRANGEBYSCORE

① ZRANGE：升序 获取指定区间内的元素（语法：ZRANGE key start stop [WITHSCORES]，withcores 参数：每个元素的下一行是它的socre

语法：ZRANGE key start stop [WITHSCORES]

• 按 升序 返回[start, stop]区间内的元素，如果带上withscores则将score一起返回。

• 此处的start和stop不是分数，而是元素的排名（下标），从0开始，支持负数

② ZREVRANGE：获取指定区间内的元素（降序），和 ZRANGE 基本没啥区别

③ ZRANGEBYSCORE：获取指定分数范围内的元素

语法：ZRANGEBYSCORE key min max [WITHSCORES] [LIMIT offset count]

• 按升序返回score在[min, max]区间内的元素，如果带上withscores则将score一起返回。
• 之前的zrange是通过元素排名返回，zrangebyscore则是通过score区间返回。
• 备注：这个命令可能在6.2.0之后废弃，并且功能合并到ZRANGE中

时间复杂度均为：O(log(N)+M)

案例如下：

127.0.0.1:6379> zrevrange myzset 0 -1 WITHSCORES
1) "one"
2) "100"
3) "two"
4) "40"127.0.0.1:6379> ZRANGEBYSCORE myzset (1 (100
1) "two"

1.4 ZPOPMAX|MIN & BZPOPMAX|MIN

① ZPOPMAX：删除并返回分数最高的count个元素

• 如果多个元素的score相同，那么会按照member的字典序进行比较，字典序高的先删除

② ZPOPMIN：删除并返回分数最小的count个元素

③ BZPOPMAX：读取并删除zset最大元素，如果没有元素则陷入阻塞

• 可以设置超时时间timeout，以秒为单位，如果超过时间了，返回nil。
• 如果超时时间设置为0，则一直阻塞，不会超时。

④ BZPOPMIN：ZPOPMIN 的阻塞版本

案例如下：

127.0.0.1:6379> zpopmax myzset
1) "one"
2) "100"
127.0.0.1:6379> bzpopmin myset 10 
(nil)
(10.03s)127.0.0.1:6379> bzpopmin myzset 10 
1) "myzset"
2) "two"
3) "40"

1.5 ZRANK & ZREVRANGE

① ZRANK：获取成员的下标

• 命令：ZRANK key member 或 ZREVRANK key member
• 返回指定元素member的排名，这个排名就是socre从小到大的顺序，从0开始排，也可以当作下标

② ZREVRANGE： 返回指定元素member的排名，这个排名就是socre从大到小的顺序，从0开始排

1.6 ZREM & ZREMRANGEBYRANK & ZREMRANGEBYSCORE

① ZREM：删除指定的元素（语法：ZREM key member [member ...]

② ZREMRANGEBYRANK：按照排名删除元素（语法：ZREMRANGE BYRANK key start stop

③ ZREMRANGEBYSCORE：按照分数删除元素（语法：ZREMRANGE BYSCORE key min max

2. 集合间操作

2.1 ZINTERSTORE – 交集

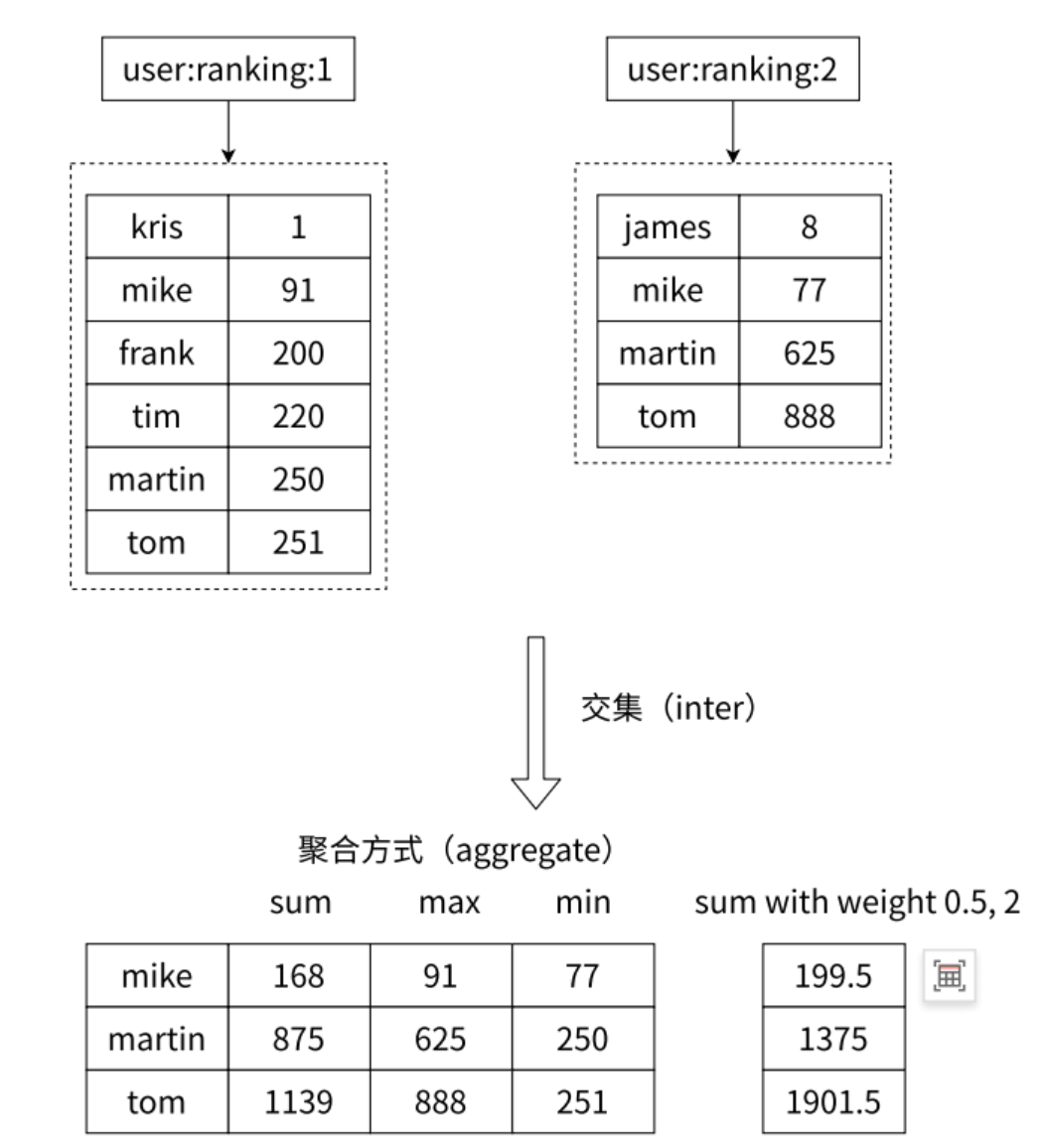
• 功能：求出给定有序集合中元素的交集并保存进⽬标有序集合中，在合并过程中以元素为单位进⾏合并，元 素对应的分数按照不同的聚合方式和权重得到新的分数

• 语法：ZINTERSTORE dest numkeys key [key ...] [WEIGHTS weight [weight ...]] [AGGREGATE]

  • 注意：numkeys必须准确填写，以便后面将参数准确解析
  • destination ：输出结果到给zset中
  • numkeys：指定后续输入的key的个数（后面会详细讲解
  • weights：权重，每一个zset都配一个weight，计算时score乘对应的weight
  • aggreate：score的合并方式
  • sum：求和（默认值）
  • min：取最小
  • max：取最大

• 返回值：目标集合中的元素个数

• 时间复杂度：$O(N\ast K)+O(M\ast log(M))$，N是输⼊的有序集合中最小的有序集合的元素个数，K是输入了几个有序集合，M是最终结果的有序集合的元素个数

这时间复杂度怎么来的？取决于源码，我们学习的是一种 解决问题 的能力，可以分解为两部分来理解：

• $O(N\ast K)$ ：这部分表示了在遍历所有输入有序集合时所需的时间。对于每个元素，都需要检查它是否存在于其他所有有序集合中。这里假设最坏情况下，每次查找操作都是线性的，即需要检查整个集合。因此，如果最小的集合有 N 个元素，而总共有 K 个集合，则总的比较次数大约为 N * K。这解释了 $O(N\ast K)$ 的部分。
• $O(M\ast log(M))$: 当确定哪些元素应该被加入到结果集中后，这些元素需要根据它们的分数进行排序以形成一个新的有序集合。即使Redis内部使用了高效的数据结构（如跳表）来保持有序性，将 M 个元素插入这样一个数据结构并保持其有序通常需要 O(M*log(M)) 的时间。这是因为每插入一个元素可能需要调整数据结构，使得插入操作平均来说接近于 log(M) 的时间复杂度。

ZINTERSTORE 操作首先通过遍历和比较各集合中的元素来找到交集成员，然后对这些成员按分数排序，从而形成了上述的时间复杂度公式。这种设计保证了即使在处理较大规模数据时也能相对高效地完成交集运算。不过，实际性能还会受到具体实现细节、数据分布等因素的影响。

样例：

127.0.0.1:6379> zadd zset1 20 a 12 b
127.0.0.1:6379> zadd zset2 1 a 5 b127.0.0.1:6379> zinterstore zset3 2 zset1 zset2 weights 1 100 aggregate sum
(integer) 2
127.0.0.1:6379> zrange zset3 0 -1 WITHSCORES
1) "a"
2) "120"
3) "b"
4) "512"

此处创建了两个zset，通过zinterstore合并，其中zset1的权重是1，zset2的权重是100，以sum方式合并。实现分数计算：最后求出交集a： 1 * 100 + 20，b： 5 * 100 + 12。

思考：关于 numkeys 参数

• 功能：numkeys 参数指定了后续参与交集运算的 key 的数量。
• 重要性：很多命令支持多个 key，如 zadd, mget, mset 等。通过 numkeys 明确指定 key 的个数可以避免选项和 keys 混淆，确保命令解析的准确性。

类比 HTTP 协议, HTTP 首行与请求头：Content-Length 字段描述了请求体（正文）的长度。

粘包问题：

• 如果缺少 Content-Length 或者数据错误，可能会导致粘包问题。
• TCP 特点：基于 TCP 的传输是面向字节流的，容易产生粘包问题。

解决粘包问题的方法

1. 明确包的长度。
2. 明确包的边界。

有序集合中的元素比较

• 成员 (member)：是有序集合中元素的本质。
• 分数 (score)：仅作为辅助排序的工具。
• 相同成员的处理：如果不同集合中的成员相同但分数不同，在进行交集合并时，最终分数如何计算取决于具体的聚合方式（如 SUM, MIN, MAX）。

有序集合的存储与权重

• 结果存储：需指定一个 key 来存储交集运算的结果。
• 权重 (weight)：在合并过程中，权重作为系数乘以当前分数，用于调整最终分数。

个人见解选择：客观因素相对稳定，而主观因素变化较大。

2.2 ZUNIONSTORE – 并集

这个参数和 zinterstore 完全一致，只是从交集变成并集。

• 功能：求出给定有序集合中元素的 并集 并保存进目标有序集合中，在合并过程中以元素为单位进行合并，元素对应的分数按照不同的聚合方式和权重得到新的分数
• 语法：ZUNIONSTORE dest numkeys key [key ...] [WEIGHTS weight [weight ...]] [AGGREGATE ]
• 返回值：目标集合中的元素个数

三、内部编码

有序集合是由 ziplist (压缩列表) 或 skiplist (跳跃表) 组成的。

1. ziplist – 压缩链表

当数据比较少时，有序集合使用的是 ziplist 存储的（减少内存使用），有序集合使用 ziplist 格式存储必须满足以下两个条件：

• 有序集合保存的元素个数要小于 zset-max-ziplist-entries 配置 (默认128个) ；
• 有序集合保存的所有元素成员的长度都必须小于 zset-max-ziplist-value配置(默认64字节) 。

2. skiplist – 跳表

如果不能满足以上两个条件中的任意一个，有序集合将会使用 skiplist 结构进行存储。

• 跳表的定义：跳表是一种特殊的链表结构，具有多层次的索引机制，类似于 B+树 的部分性质。
• 查询效率：由于采用了多层次索引，跳表在查询元素时的时间复杂度为 O(logN)，这意味着随着数据量的增长，查询效率仍然保持较高的水平。
• 适用场景：结合了链表和树的优点，提供了一种高效的范围查询解决方案，尤其适合大数据量下的范围查询需求。

关于 vs B+

特点：

• 平衡性：B+树是一种自平衡的多路搜索树，每个节点可以有多个子节点，这使得树的高度保持较低。
• 键值分布：所有键值都出现在叶子节点上，非叶子节点仅作为索引使用。
• 有序性：叶子节点通过指针链接起来，形成一个有序链表，便于范围查询。
• 磁盘友好：B+树的设计特别适合于磁盘等块设备的访问模式，因为它的节点大小通常与磁盘页大小相匹配，从而减少了I/O操作次数。

优点：

• 高效的范围查询：由于叶子节点是相连的，因此可以快速地进行范围扫描。
• 适用于数据库和文件系统：非常适合需要频繁读取和写入大量数据的应用场景。

缺点：

• 插入和删除操作可能较复杂：当节点满时需要分裂，空闲时需要合并或重新分配。
• 实现较为复杂：涉及到节点分裂、合并等操作，实现起来比跳表更复杂。

四、使用场景

1. 排行榜系统

有序集合比较典型的使用场景就是排行榜系统。例如学生成绩的排名。某视频(博客等)网站的用户点赞、播放排名、电商系统中商品的销量排名等。我们以博客点赞为例。

① 添加用户赞数：例如小编Tom发表了一篇博文，并且获得了10个赞。

Copyzadd user:ranking arcticle1 10

② 取消用户赞数：这个时候有一个读者又觉得Tom写的不好，又取消了赞，此时需要将文章的赞数从榜单中减去1，可以使用zincrby。

Copyzincrby user:ranking arcticle1 -1

③ 查看某篇文章的赞数

CopyZSCORE user:ranking arcticle1

④ 展示获取赞数最多的十篇文章：此功能使用zrevrange命令实现：

Copyzrevrangebyrank user:ranking  0 9

2. 电话号码(姓名)排序

使用有序集合的 ZRANGEBYLEX 或 ZREVRANGEBYLEX 可以帮助我们实现电话号码或姓名的排序,我们以ZRANGEBYLEX为例
注意：不要在分数不一致的SortSet集合中去使用 ZRANGEBYLEX和 ZREVRANGEBYLEX 指令,因为获取的结果会不准确。

① 电话号码排序：我们可以将电话号码存储到SortSet中,然后根据需要来获取号段:

Copyredis> zadd phone 0 13100111100 0 13110114300 0 13132110901 
(integer) 3
redis> zadd phone 0 13200111100 0 13210414300 0 13252110901 
(integer) 3
redis> zadd phone 0 13300111100 0 13310414300 0 13352110901 
(integer) 3

② 获取所有号码:

Copyredis> ZRANGEBYLEX phone - +
1) "13100111100"
2) "13110114300"
3) "13132110901"
4) "13200111100"
5) "13210414300"
6) "13252110901"
7) "13300111100"
8) "13310414300"
9) "13352110901"

③ 获取132号段:

Copyredis> ZRANGEBYLEX phone [132 (133
1) "13200111100"
2) "13210414300"
3) "13252110901"

④ 获取132、133号段:

Copyredis> ZRANGEBYLEX phone [132 (134
1) "13200111100"
2) "13210414300"
3) "13252110901"
4) "13300111100"
5) "13310414300"
6) "13352110901"

⑤ 姓名排序：将名称存储到SortSet中:

Copyredis> zadd names 0 Toumas 0 Jake 0 Bluetuo 0 Gaodeng 0 Aimini 0 Aidehua 
(integer) 6

⑥ 获取所有人的名字:

Copyredis> ZRANGEBYLEX names - +
1) "Aidehua"
2) "Aimini"
3) "Bluetuo"
4) "Gaodeng"
5) "Jake"
6) "Toumas"

⑦ 获取名字中大写字母A开头的所有人:

Copyredis> ZRANGEBYLEX names [A (B
1) "Aidehua"
2) "Aimini"

⑧ 获取名字中大写字母C到Z的所有人:

Copyredis> ZRANGEBYLEX names [C [Z
1) "Gaodeng"
2) "Jake"
3) "Toumas"

小结

本篇文章我们总结了Redis 有序集合对象的内部实现、常用命令以及常用的一些场景，有序集合提供了获取指定分数和元素范围查询、计算成员排名等功能，合理的利用有序集合，能帮助我们在实际开发中解决很多问题。那么大家在项目中对Redis有序集合对象的使用都有哪些场景呢，欢迎在评论区给我留言和分享，我会第一时间反馈！我们共同学习与进步！