《计算机组成原理与汇编语言程序设计》实验报告二 基本数字逻辑及汉字显示
目 录
一、实验学时
二、实验目的
三、实验要求
四、实验内容
五、实验步骤
1、打开Logisim软件,列出并行四位二进制全加器逻辑电路真值表,并使用与、或、非、异或等基本原件实现并行四位二进制全加器逻辑电路,铺设完成后进行测试进而判断电路是否铺设成功。
2、打开Logisim软件,在第一步实现的并行四位二进制全加器的基础上构建包括溢出、符号、归零、进位等检测功能的四位二进制运算器,铺设完成后进行测试进而判断电路是否铺设成功。
3、打开Logisim软件,利用两个四位二进制加法器实现八位串行加法器,列出八位串行加法器逻辑电路真值表,并使用两个四位二进制加法器实现八位串行加法器逻辑电路,铺设完成后进行测试进而判断电路是否铺设成功。
4、打开Logisim软件,利用两个四位二进制加法器实现八位并行加法器,列出八位并行加法器逻辑电路真值表,并使用两个四位二进制加法器实现八位并行加法器逻辑电路,铺设完成后进行测试进而判断电路是否铺设成功。
5、打开Logisim软件,用自己学号(20212501238)最后两位数字(38)转化为二进制(00000011,00001000)作为输入,测试两个八位加法器的功能。
六、实验小结
1、问题和解决方法:
2、心得体会:
一、实验学时
课堂2学时,课后2学时
二、实验目的
1) 熟悉Logisim软件的使用方法。
2) 掌握四位全加器逻辑电路实现方法。
3) 掌握八位全加器设计。
三、实验要求
1)做好实验预习,复习基本数字逻辑电路的原理,掌握实验元器件的功能特性。
2)按照实验内容与步骤的要求,独立思考,认真仔细地完成实验。
3)书写实验报告。
四、实验内容
四位并行加法器电路图如下:
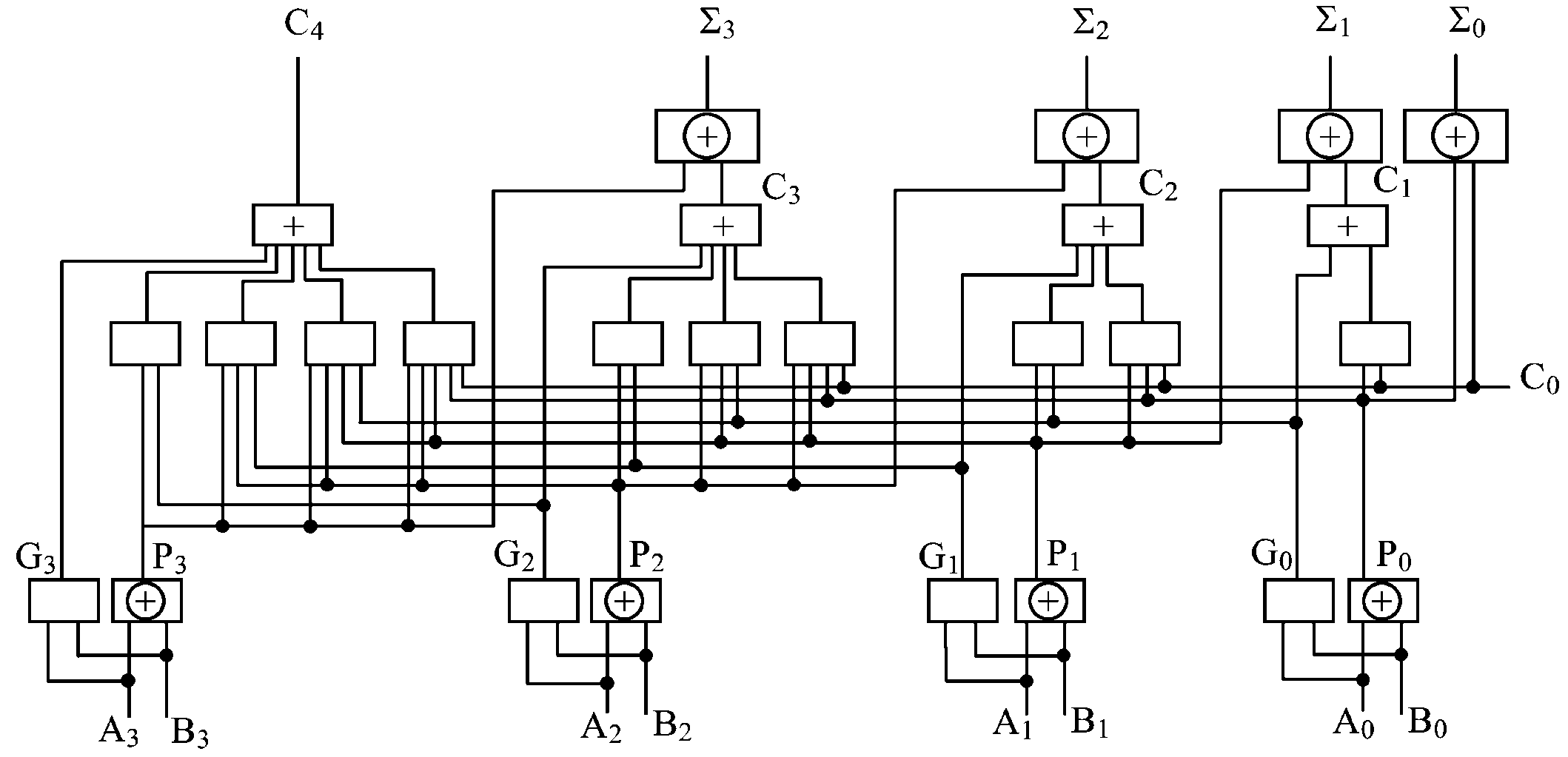
图4-1 四位并行全加器电路图
1、请按照给定的电路图在logisim下实现4位2进制全加器仿真电路,并进行功能验证。
2、请在完成第一步的基础上,构建包括溢出、符号、归零、进位等检测功能的四位二进制运算器,具体功能如下示意图所示,请完成Logisim仿真电路搭建及功能验证。
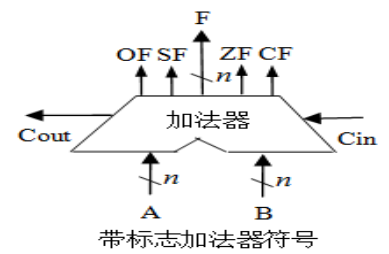
图4-2 所需电路及工作区
3、利用两个四位二进制运算器,分别实现八位串行加法器、八位并行加法器。
4、用自己学号最后两位数字转化为二进制作为输入,测试两个八位加法器功能。记录各输出端结果。
五、实验步骤
1、打开Logisim软件,列出并行四位二进制全加器逻辑电路真值表,并使用与、或、非、异或等基本原件实现并行四位二进制全加器逻辑电路,铺设完成后进行测试进而判断电路是否铺设成功。
(1)使用逻辑公式G=AB,P=A⨁B,CI=G+PC(G为A与【AND】B后的结果值,P为A异或B的结果值,CI为先P与【AND】C再和G进行或操作【OR】后得到的结果值,⊕为异或符号,C为低位的进位,CI为高位的进位)完成对并行四位二进制全加器逻辑电路的实现,对应的部分并行四位二进制全加器逻辑电路真值表如图5-1-1所示:
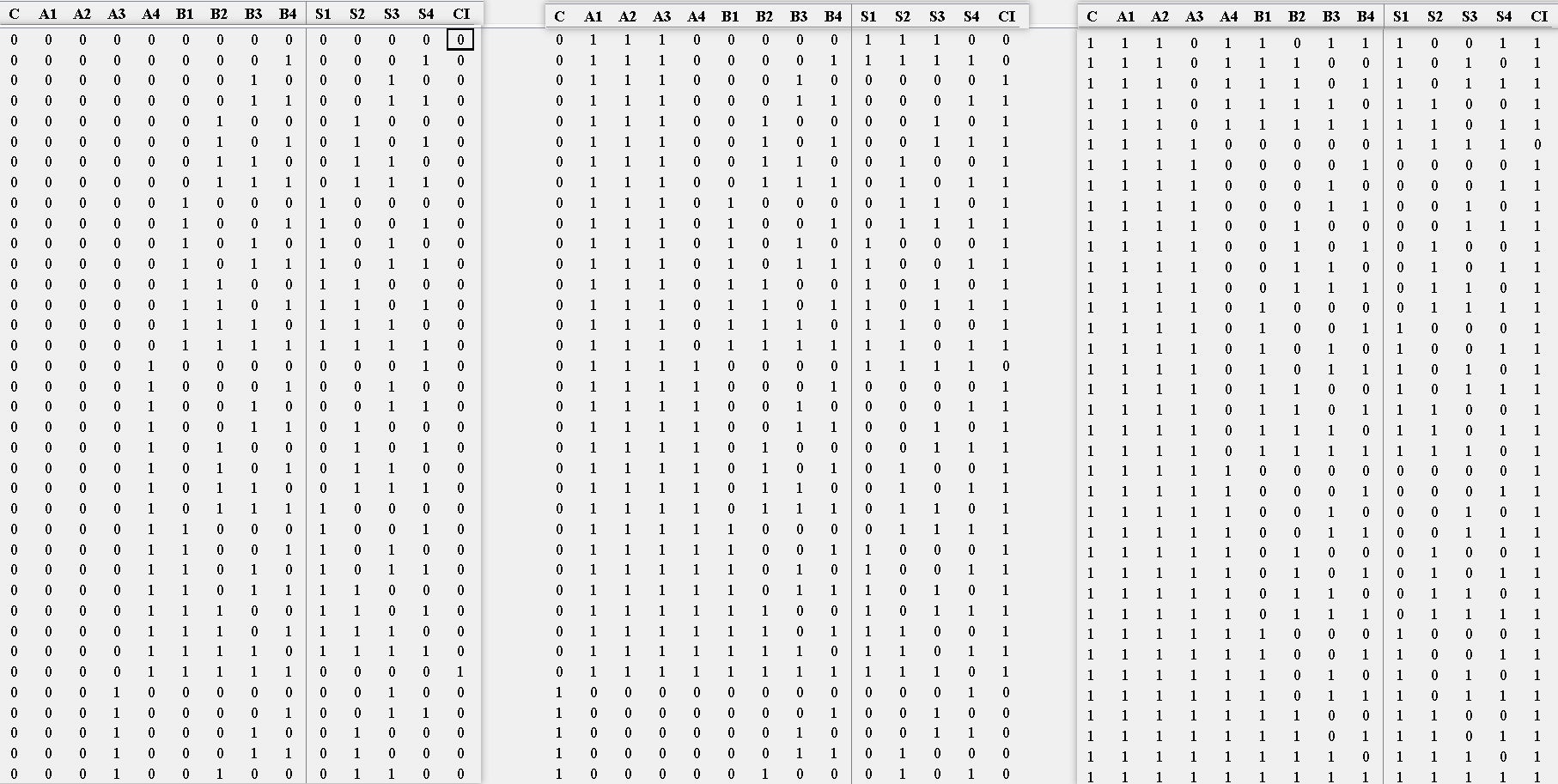
图5-1-1 并行四位二进制全加器逻辑电路真值表
(2)依据逻辑公式完成并行四位二进制全加器逻辑电路的架构,输入端A1、B1、C,先让A1和B1进行与操作后得到G1;再让A1和B1进行异或操作后得到P1;然后让P1和C进行与操作后再和G1进行或操作得到CI;最后将P1和C进行异或操作后得到S1,在运行过程中低位的高位进位是高位的低位进位,依次类推到A4和B4,对应的并行四位二进制全加器逻辑电路如图5-1-2所示:
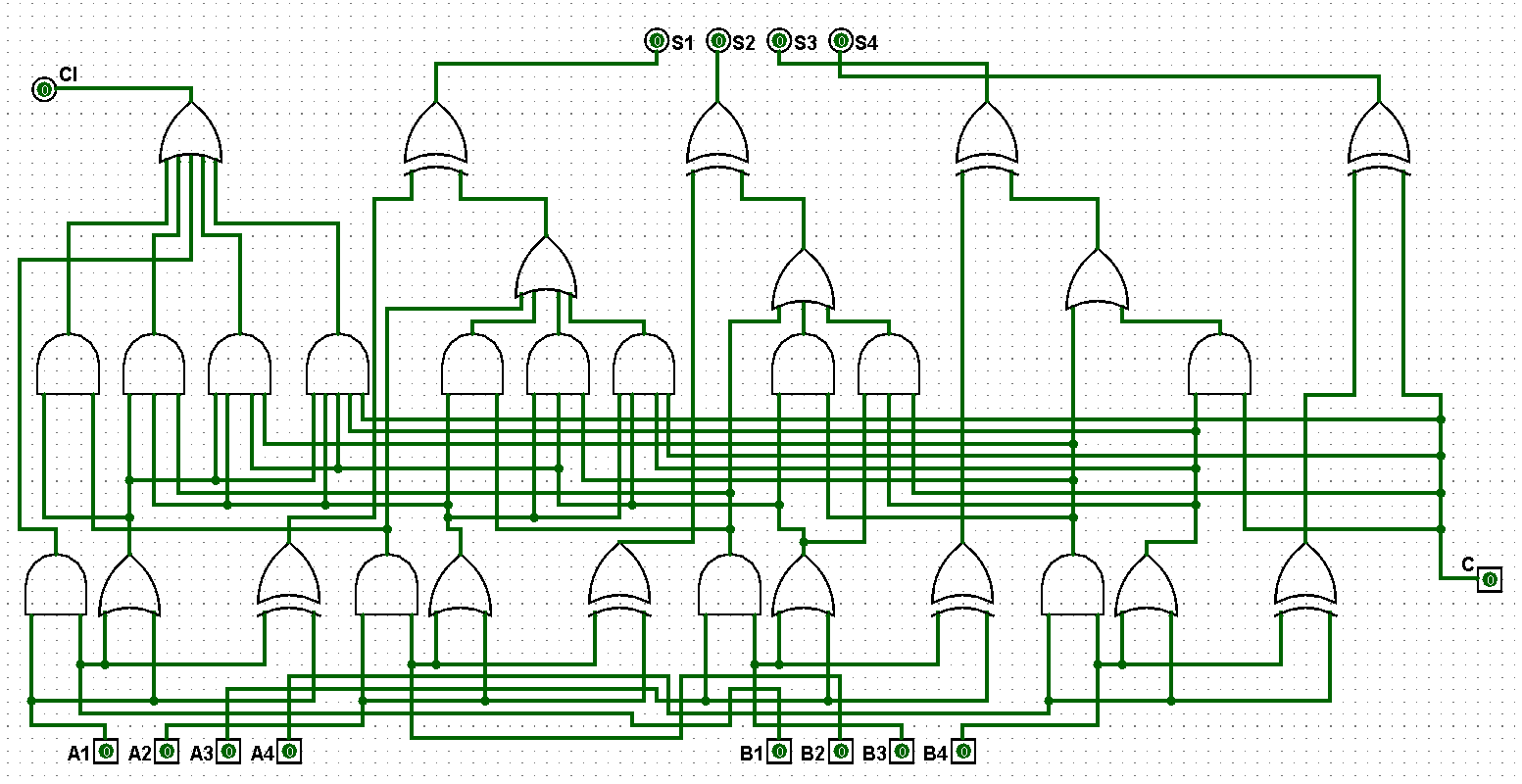
图5-1-2 并行四位二进制全加器逻辑电路
(3)并行四位二进制全加器逻辑电路铺设完毕后进行测试,进而判断自己的电路是否铺设成功,经过测试后此电路状态一切正常,对应的并行四位二进制全加器逻辑电路测试如图5-1-3至5-1-10所示:
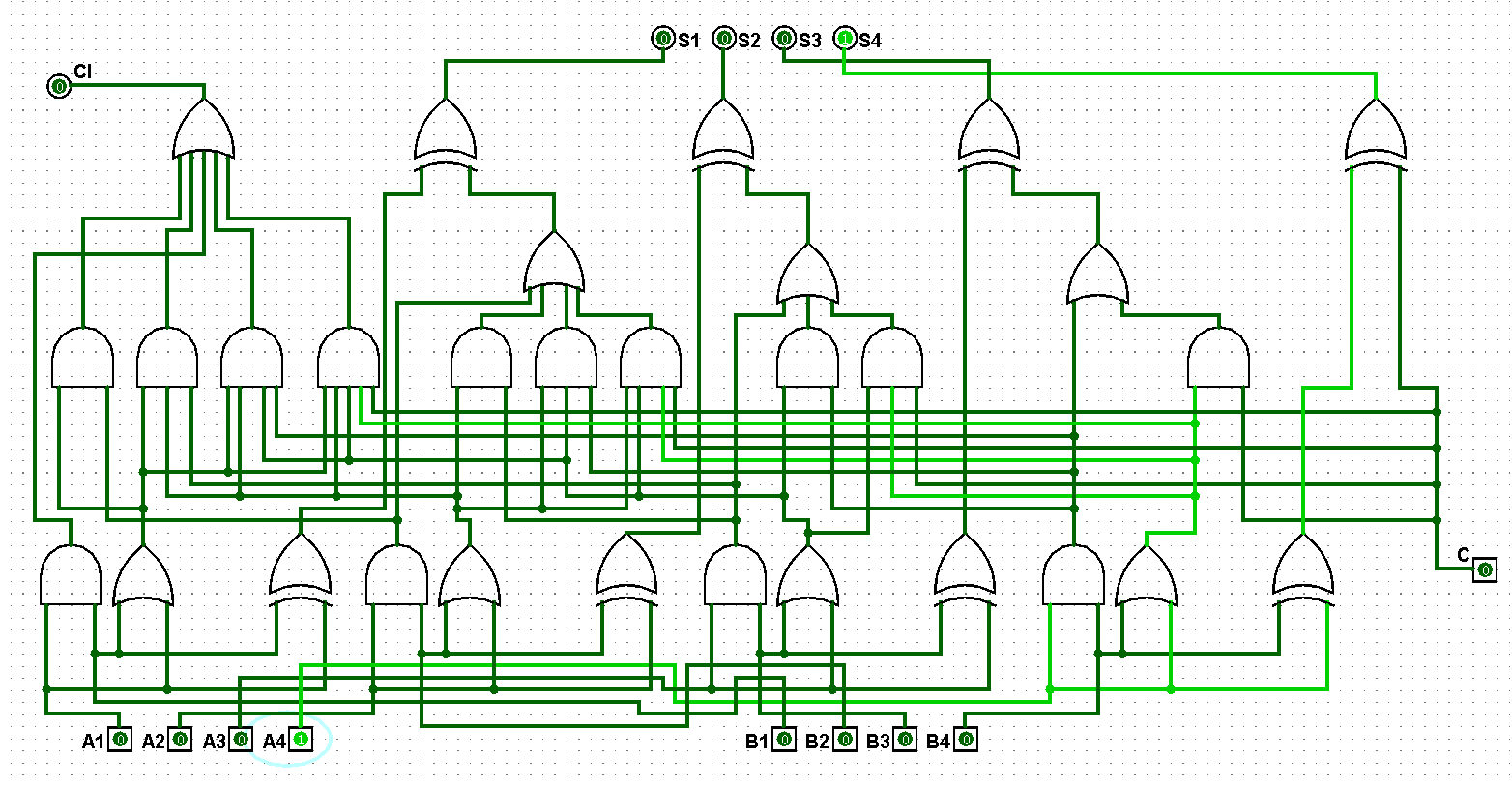
图5-1-3 并行四位二进制全加器测试1+0=1
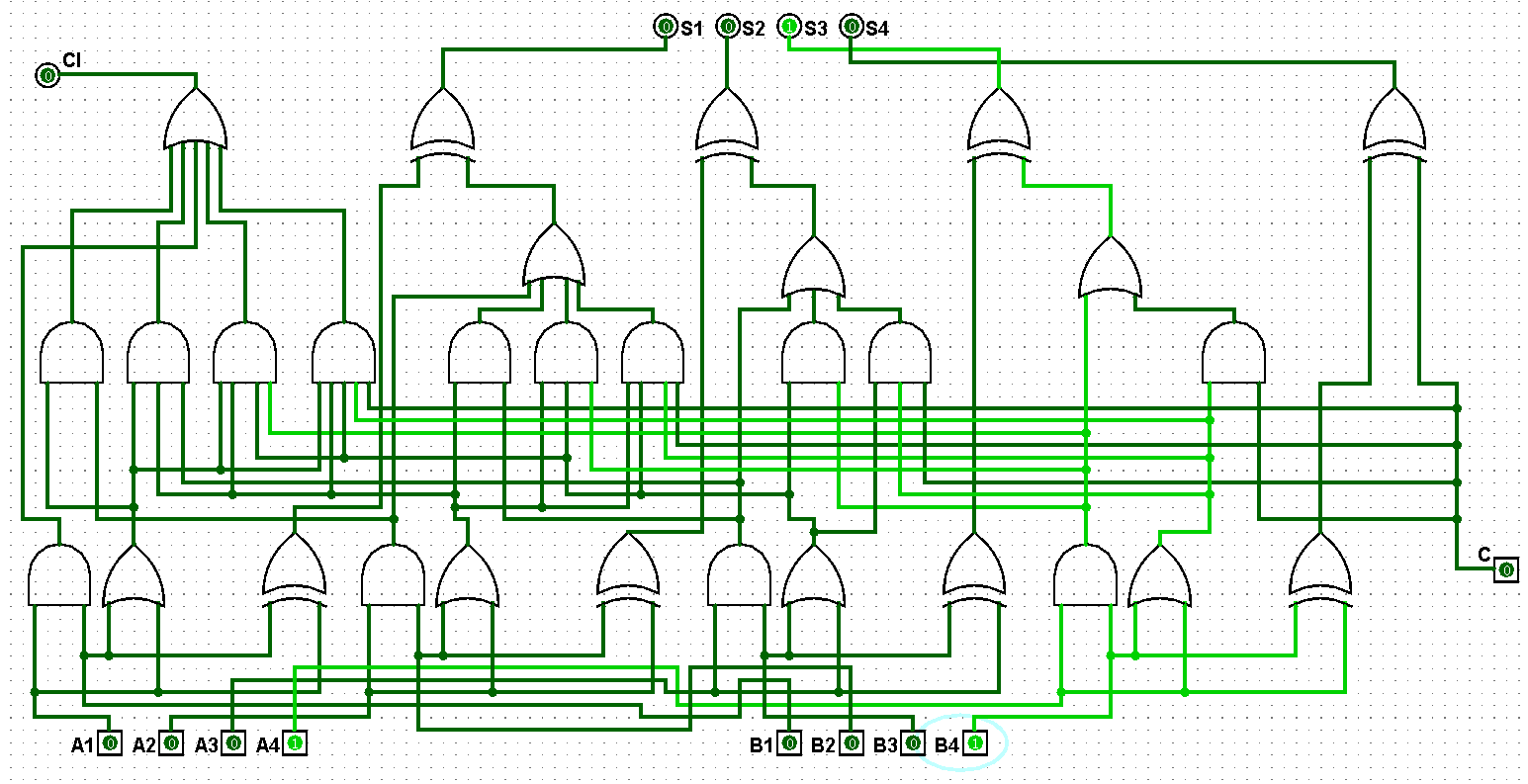
图5-1-4 并行四位二进制全加器测试1+1=2
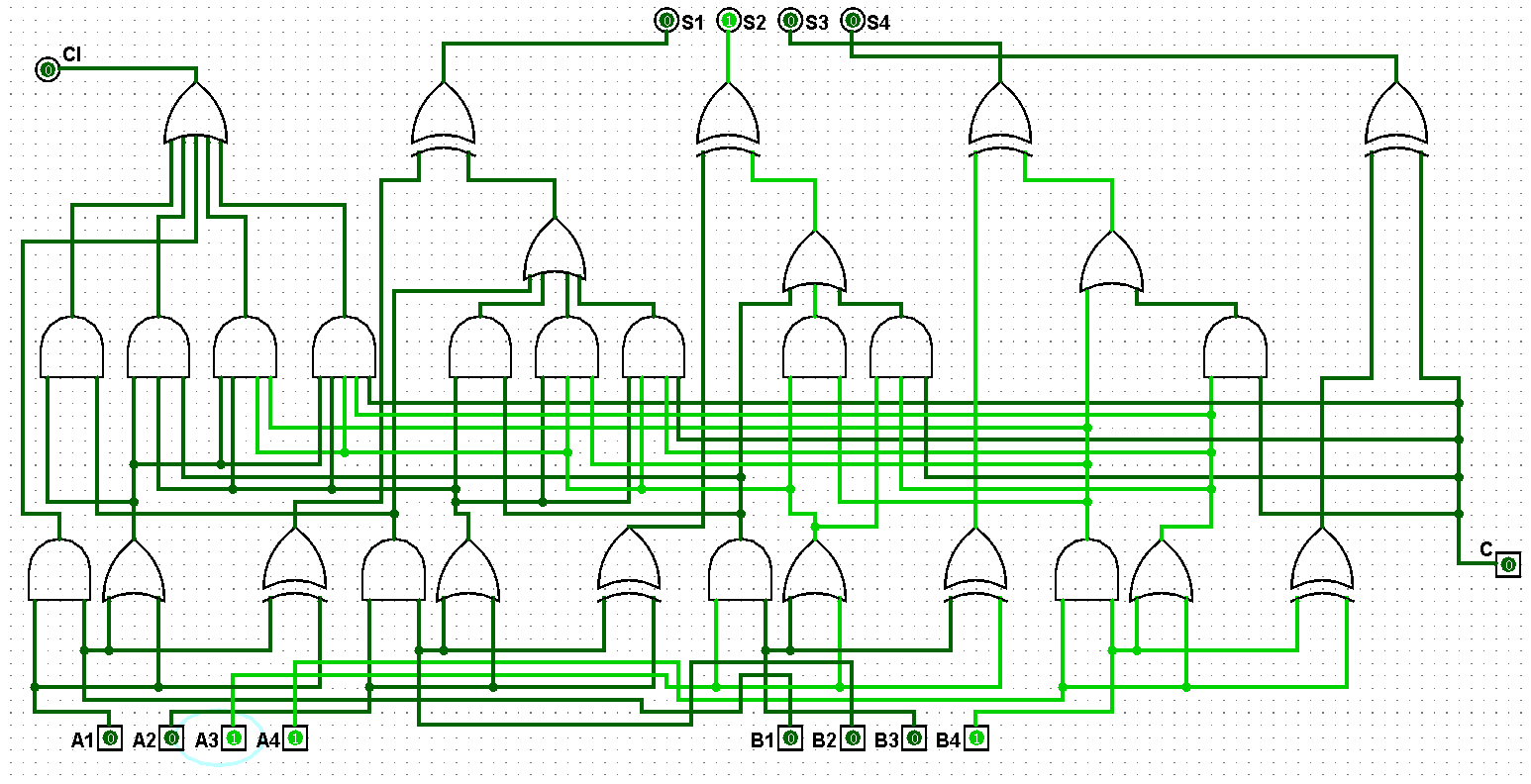
图5-1-5 并行四位二进制全加器测试3+1=4
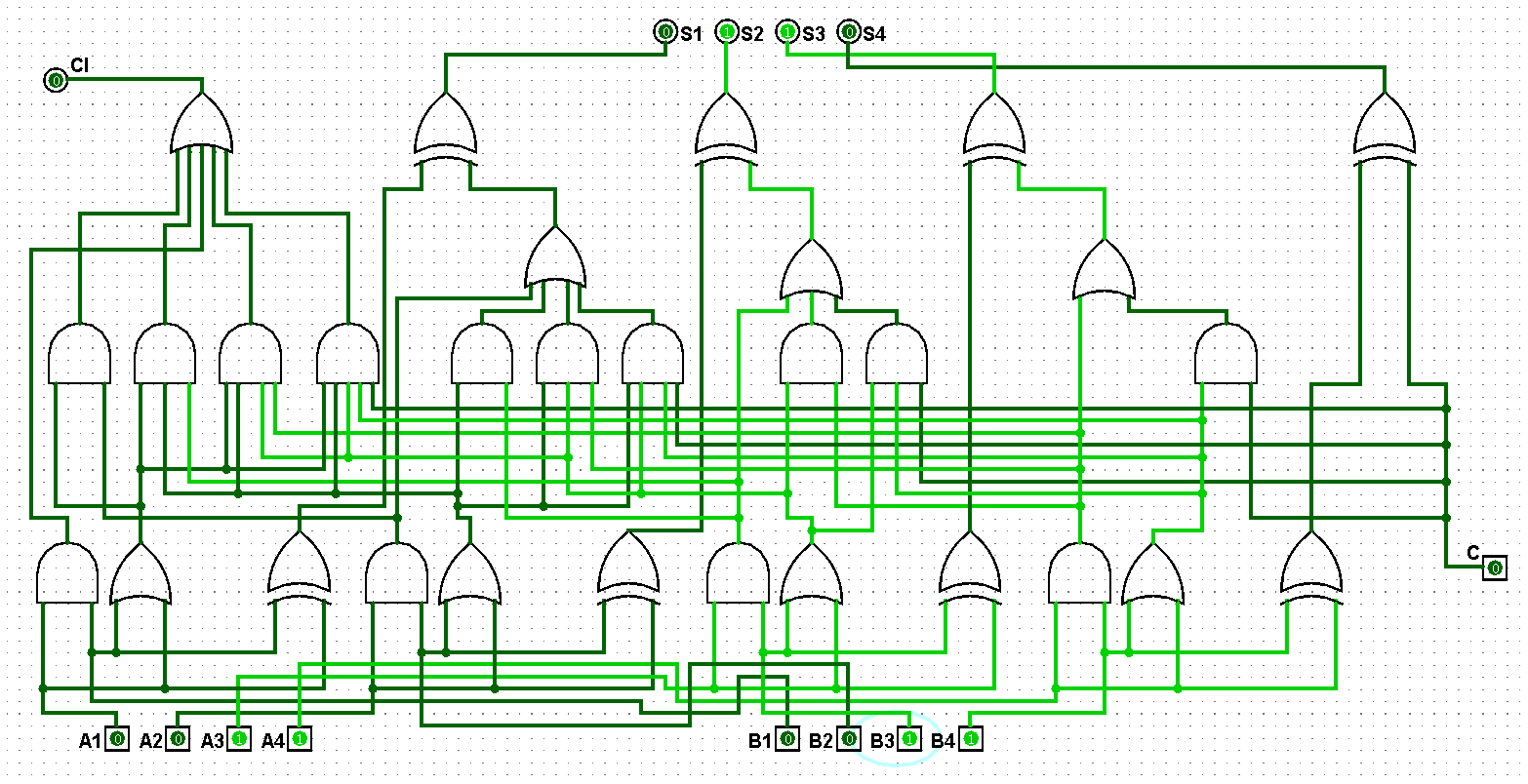
图5-1-6 并行四位二进制全加器测试3+3=6
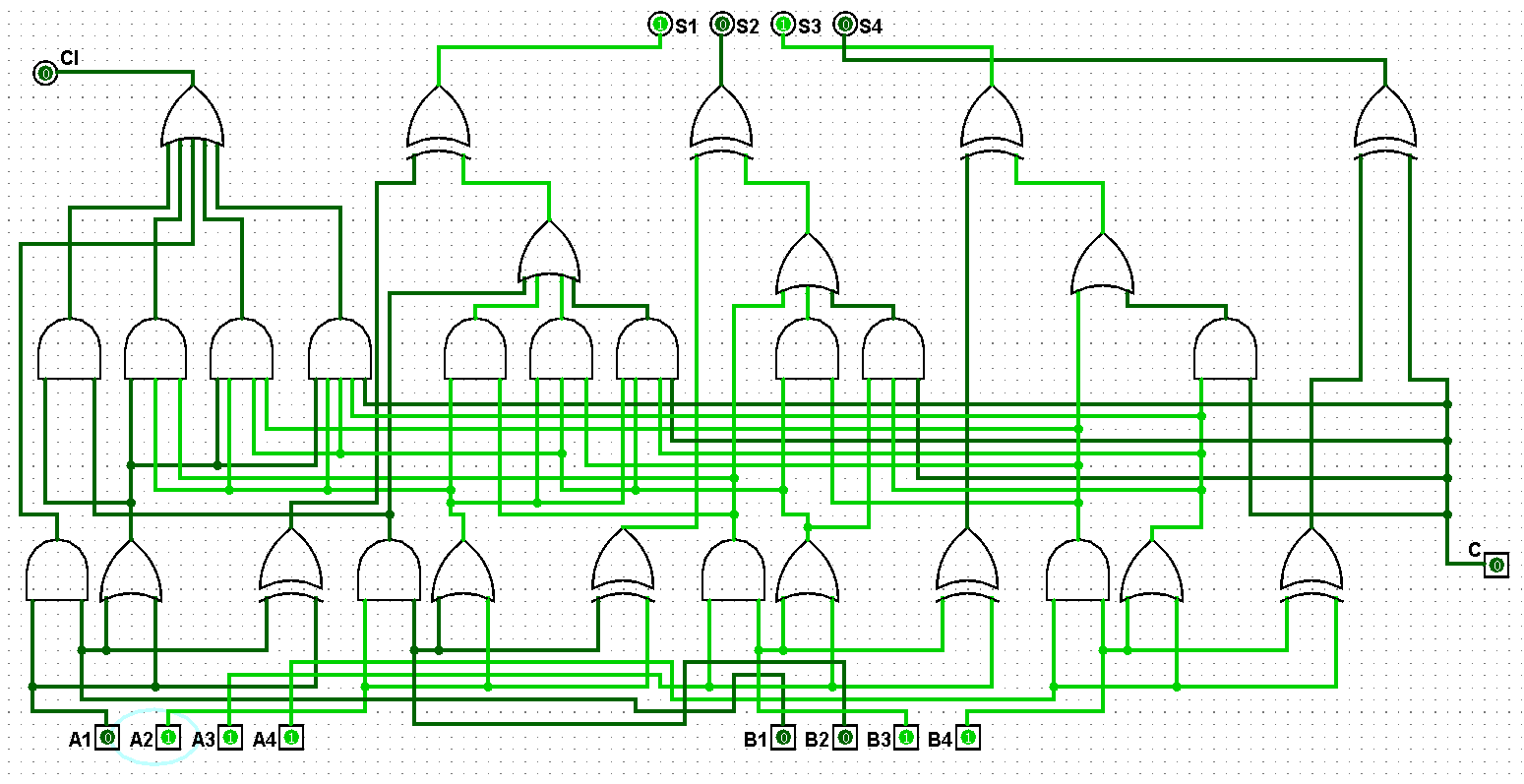
图5-1-7 并行四位二进制全加器测试7+3=10
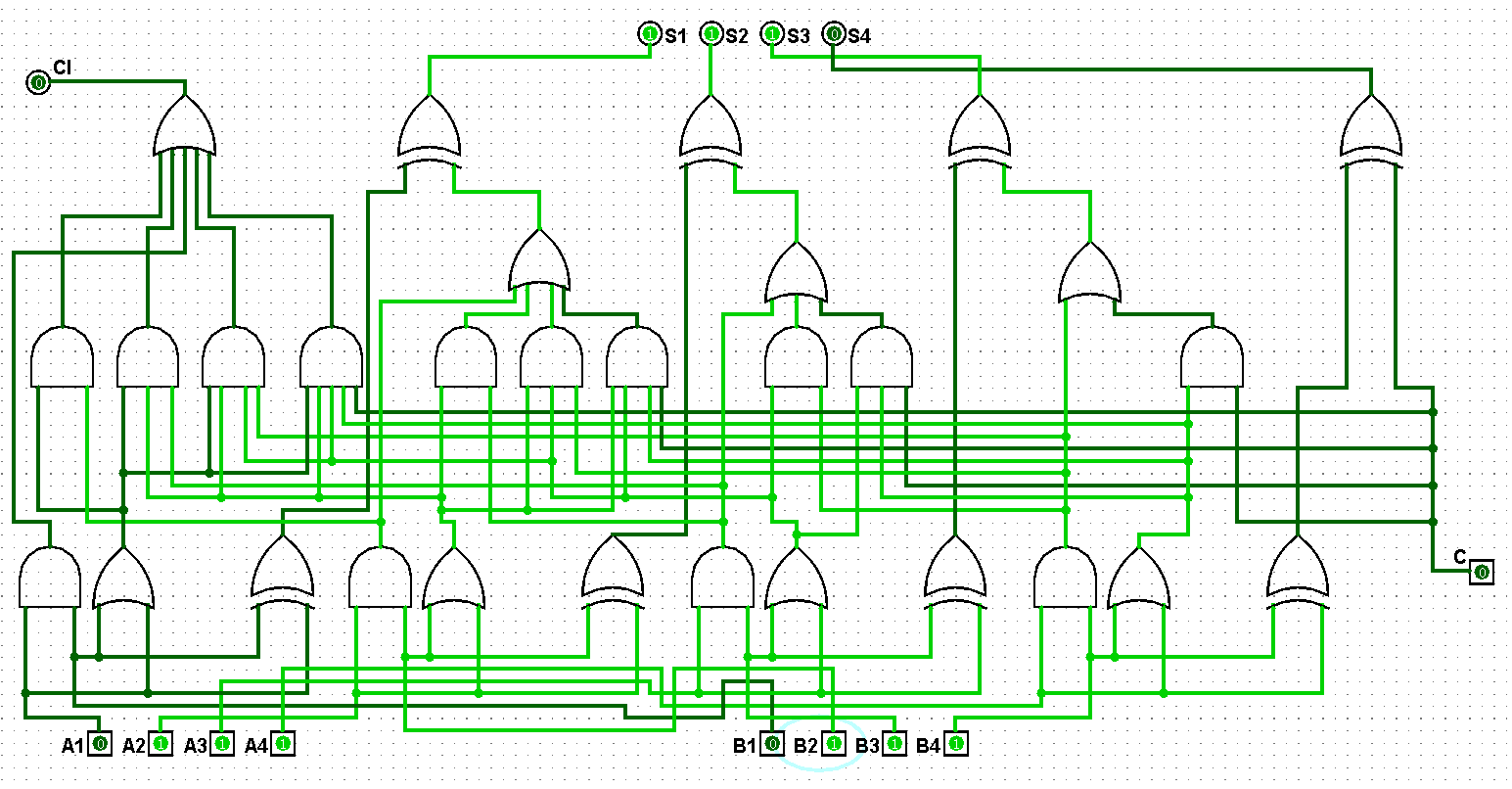
图5-1-8 并行四位二进制全加器测试7+7=14
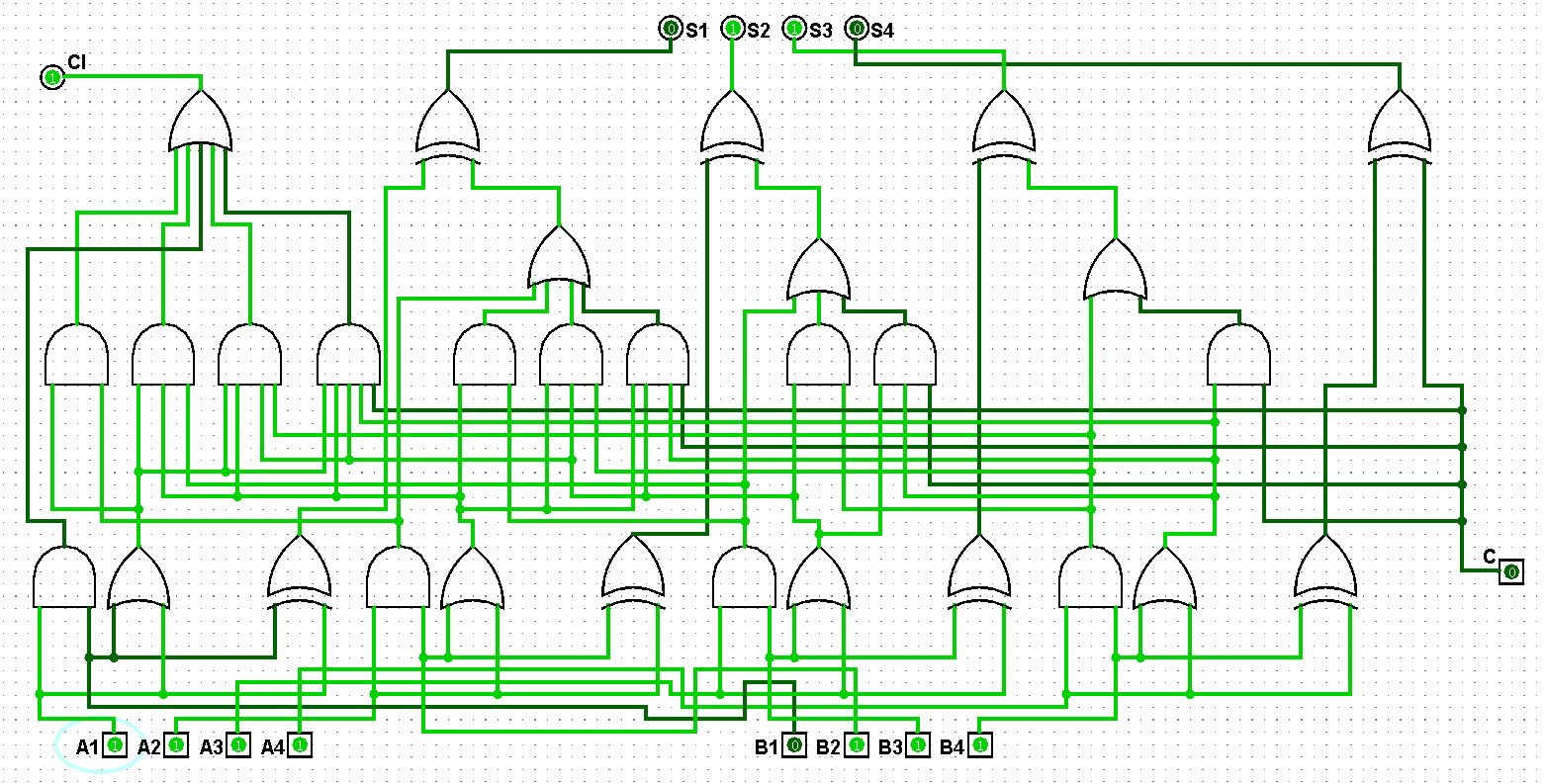
图5-1-9 并行四位二进制全加器测试15+7=22
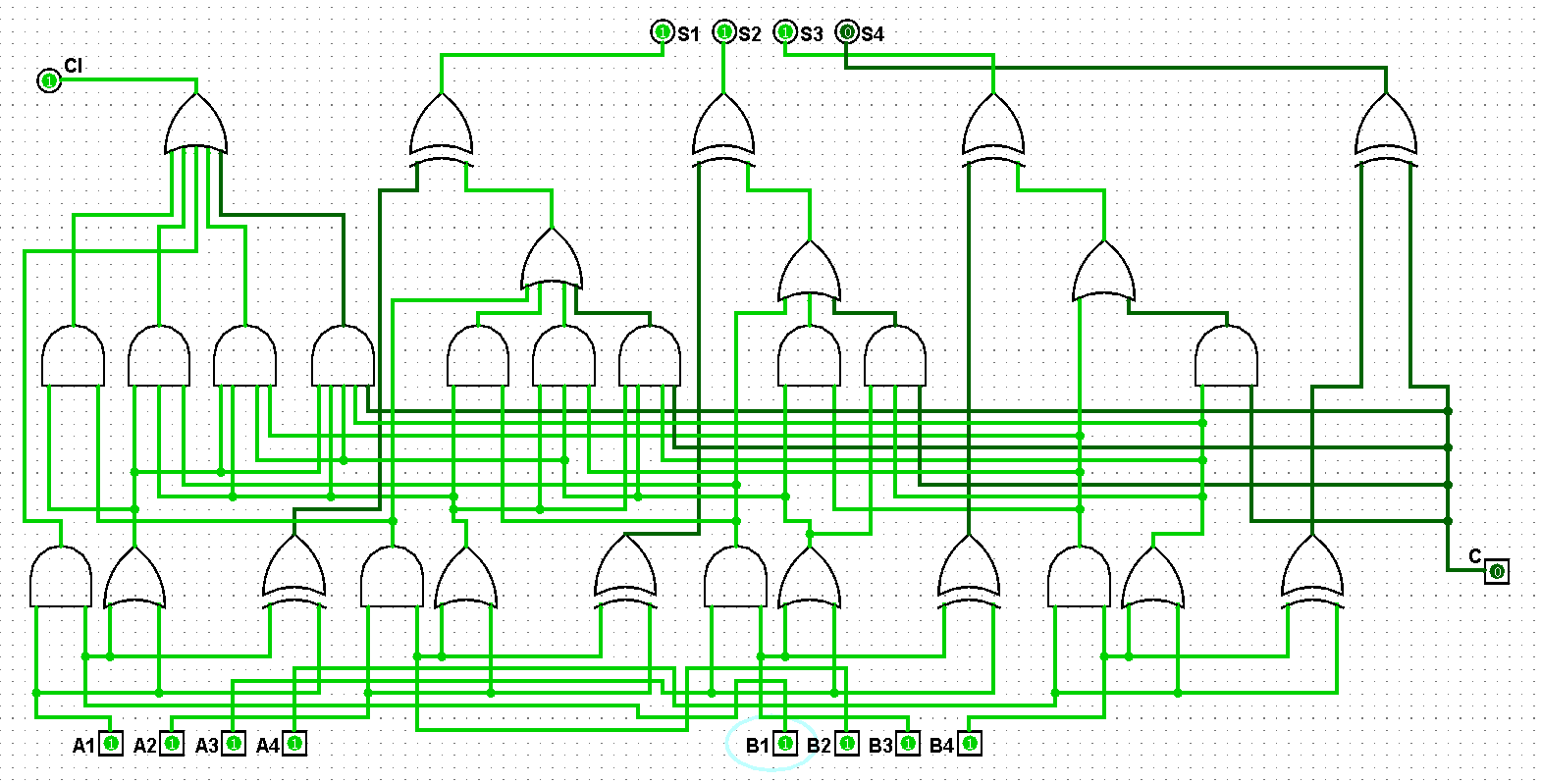
图5-1-10 并行四位二进制全加器测试15+15=30
2、打开Logisim软件,在第一步实现的并行四位二进制全加器的基础上构建包括溢出、符号、归零、进位等检测功能的四位二进制运算器,铺设完成后进行测试进而判断电路是否铺设成功。
(1)使用溢出逻辑公式OF=A’B’S+ABS’(A’、B’、S’分别表示对A、B、S进行非操作后的结果,S表示A和B进行运算的结果)完成对溢出功能的实现,当有效位的结果值全部为0时ZF=1,否则ZF=0;通过最高位的进位进行对符号和进位的判断,如果是0表示为+并没有进位,否则为-并进行了进位(OF表示溢出标志,ZF表示零标志,SF表示符号标志,CF表示进位标志),对应的部分四位二进制运算器逻辑电路真值表如图5-2-1所示:
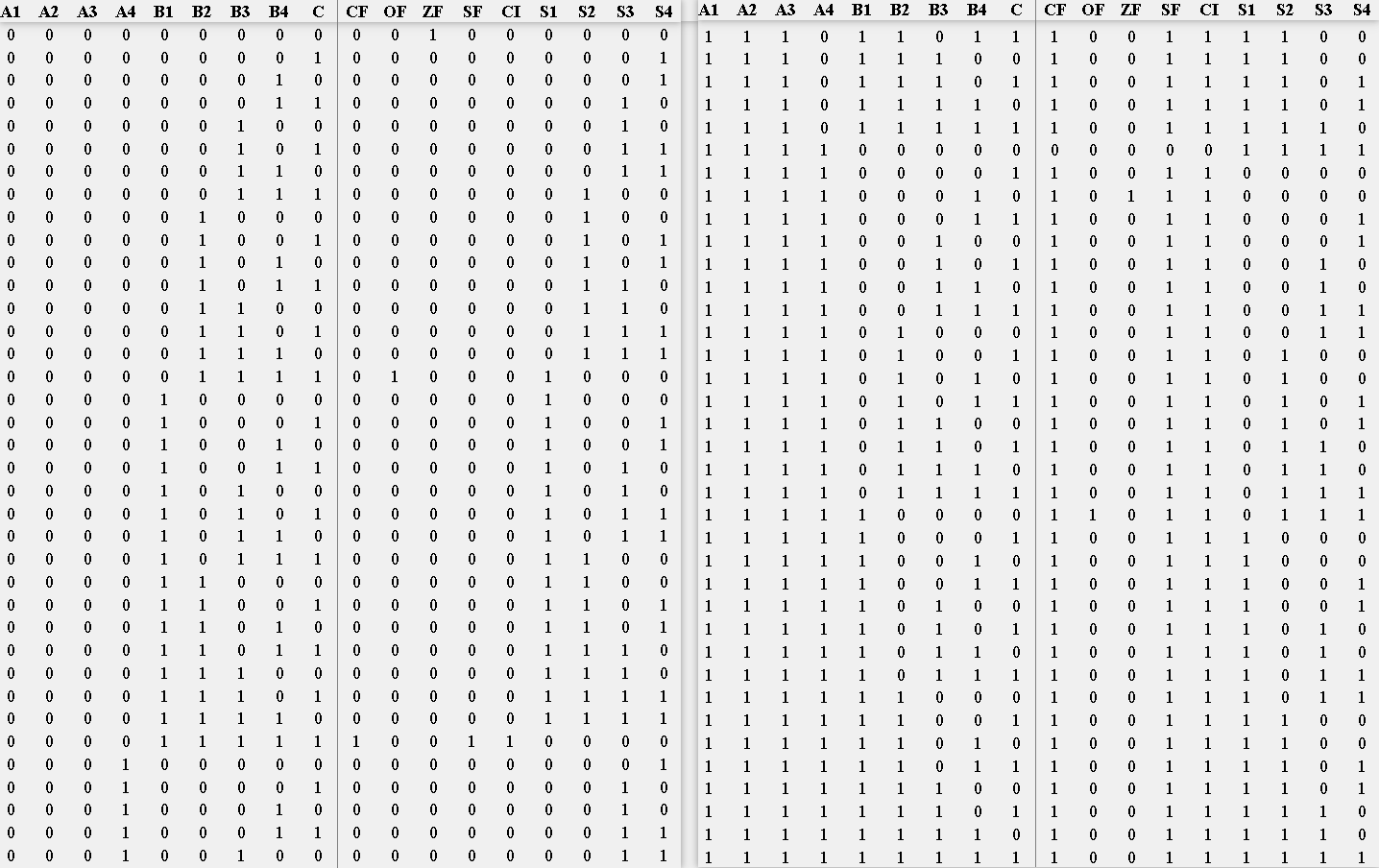
图5-2-1 四位二进制运算器逻辑电路真值表
(2)依据逻辑公式完成四位二进制运算器逻辑电路的架构,将最高位A4、B4分别进行非操作后和S4进行与操作,再将S进行非操作后和A4、B4进行与操作,最后将两个结果进行或操作得到溢出标志OF;将输出值S1、S2、S3、S4进行或非操作后得到零标志ZF;通过最高位的进位得到符号标志SF和进位标志CF,对应的四位二进制运算器逻辑电路如图5-2-2所示:

图5-2-2 四位二进制运算器逻辑电路
(3)四位二进制运算器逻辑电路铺设完毕后进行测试,进而判断自己的电路是否铺设成功,经过测试后此电路状态一切正常,对应的四位二进制运算器逻辑电路测试如图5-2-3至5-2-11所示:
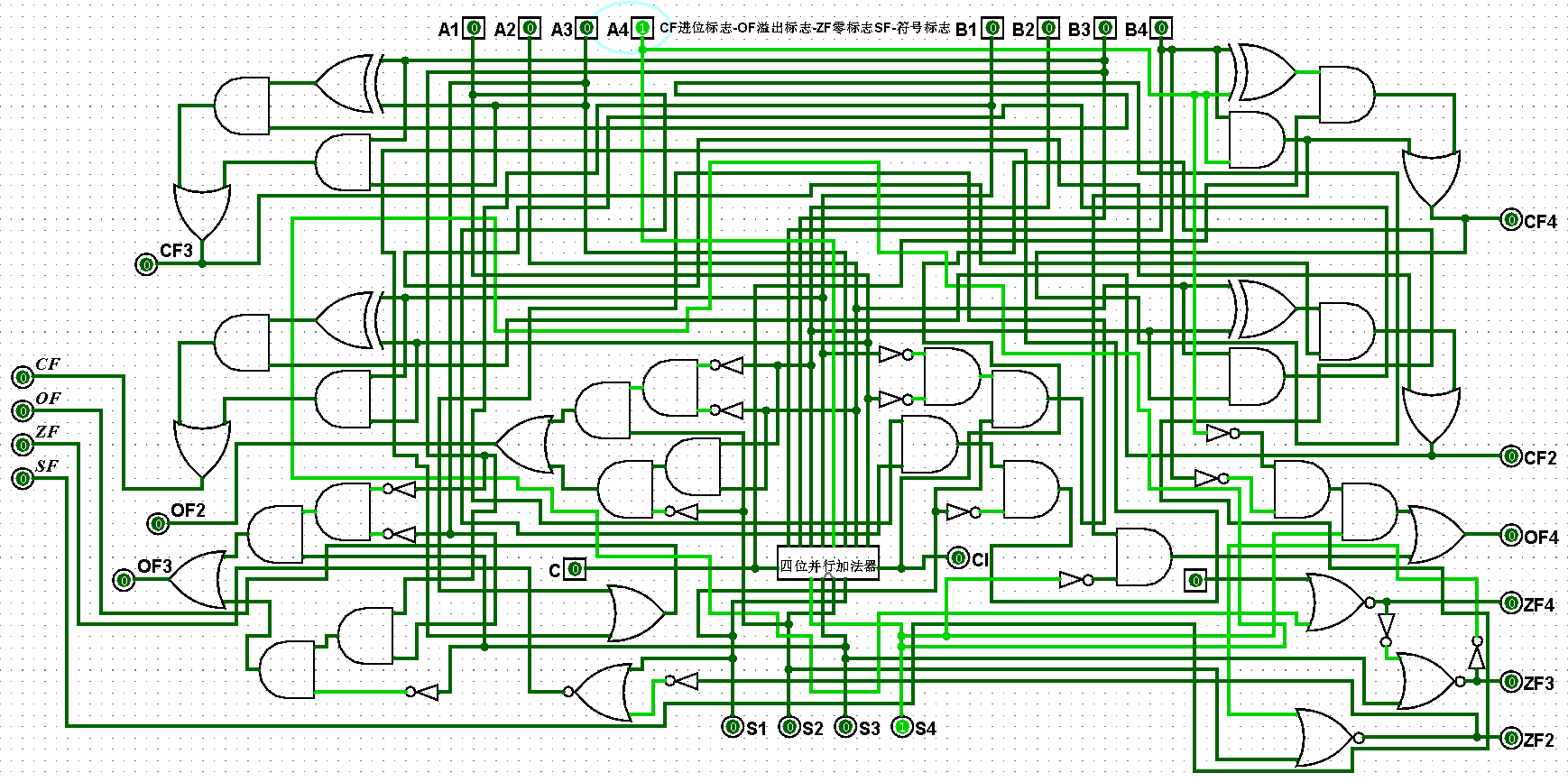
图5-2-3 四位二进制运算器测试1+0=1,CF=0,OF=0,ZF=0,SF=0
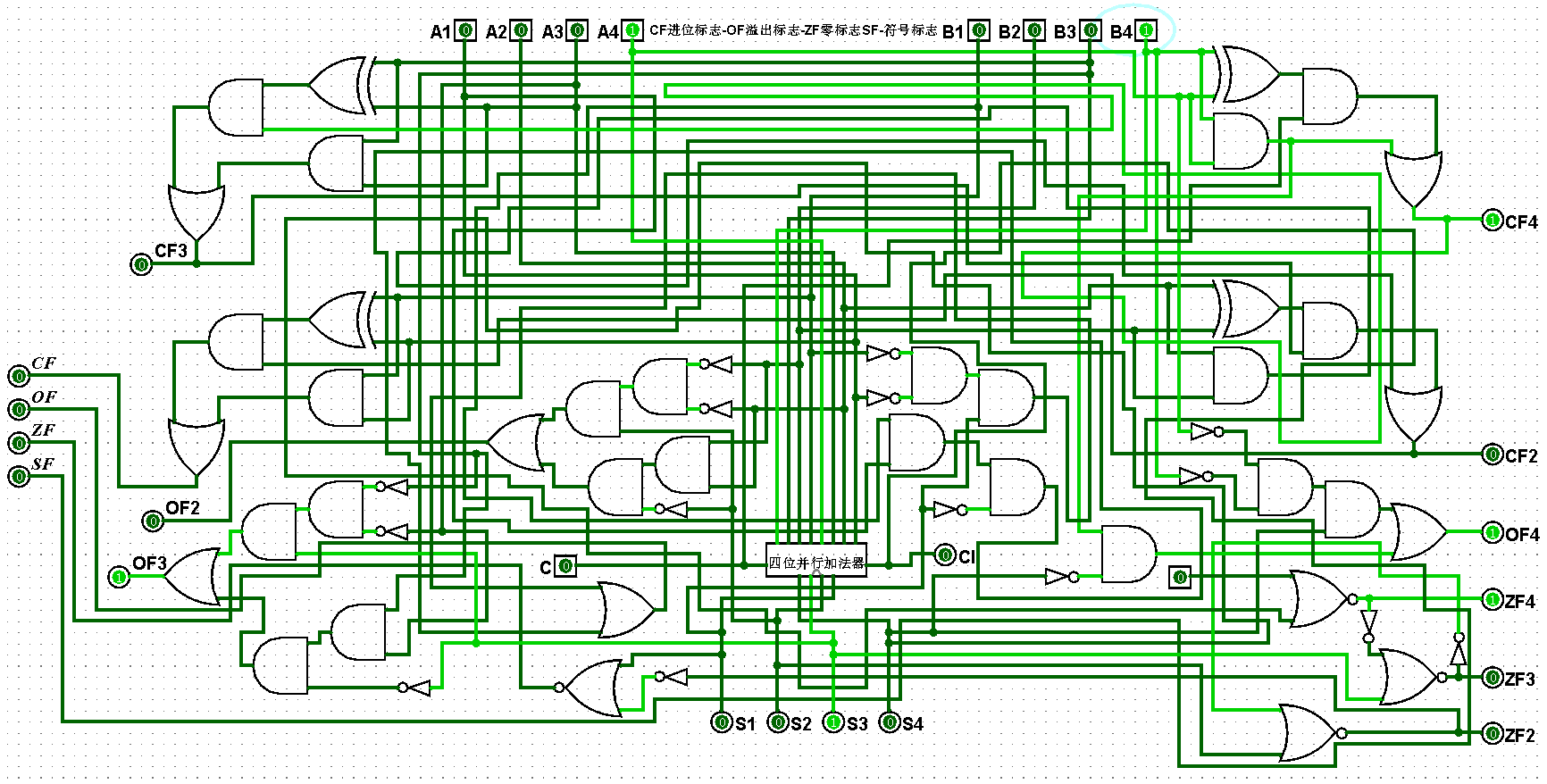
图5-2-4 四位二进制运算器测试1+1=2,CF=0,OF=0,ZF=0,SF=0
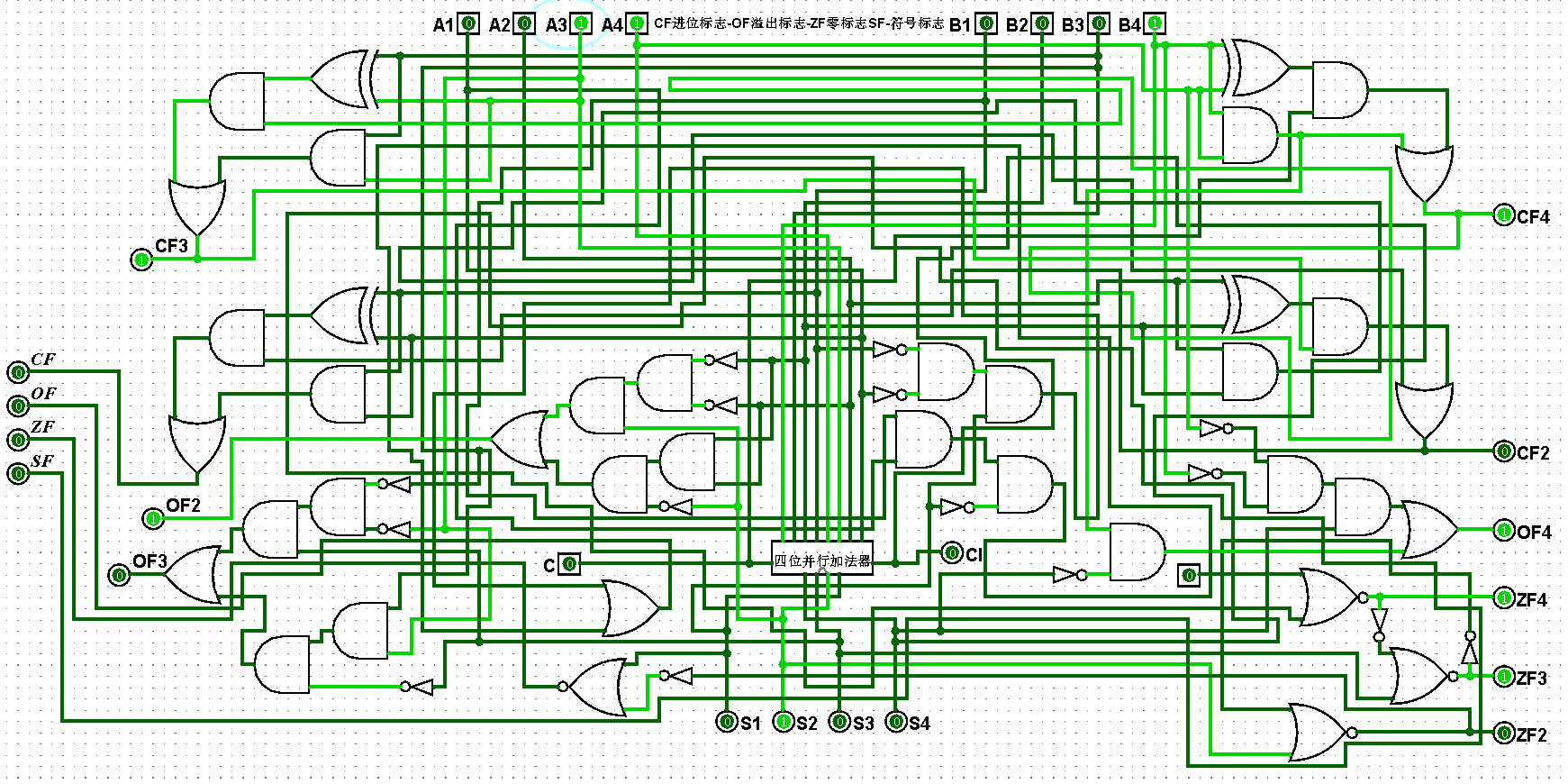
图5-2-5 四位二进制运算器测试3+1=4,CF=0,OF=0,ZF=0,SF=0
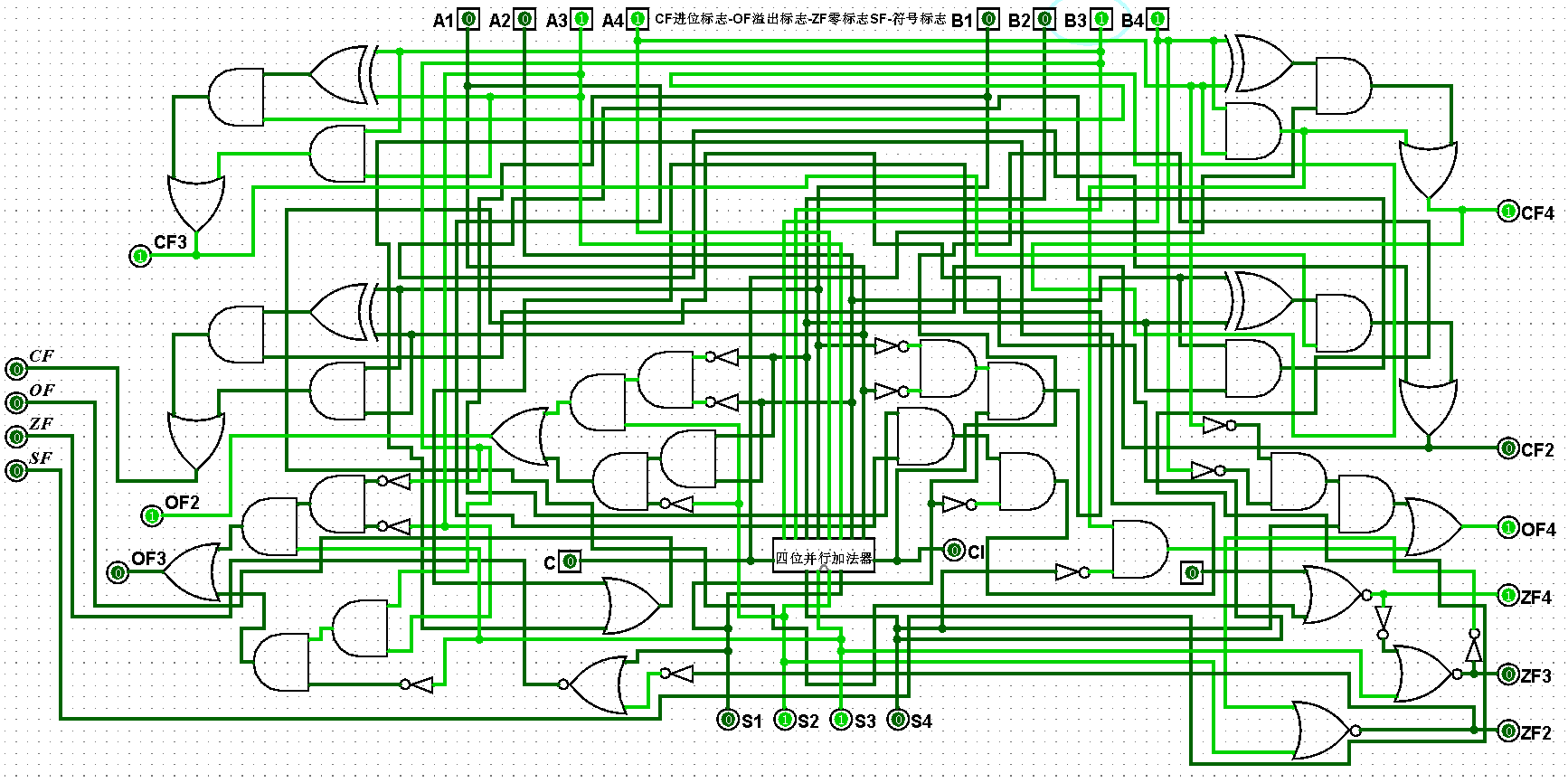
图5-2-6 四位二进制运算器测试3+3=6,CF=0,OF=0,ZF=0,SF=0
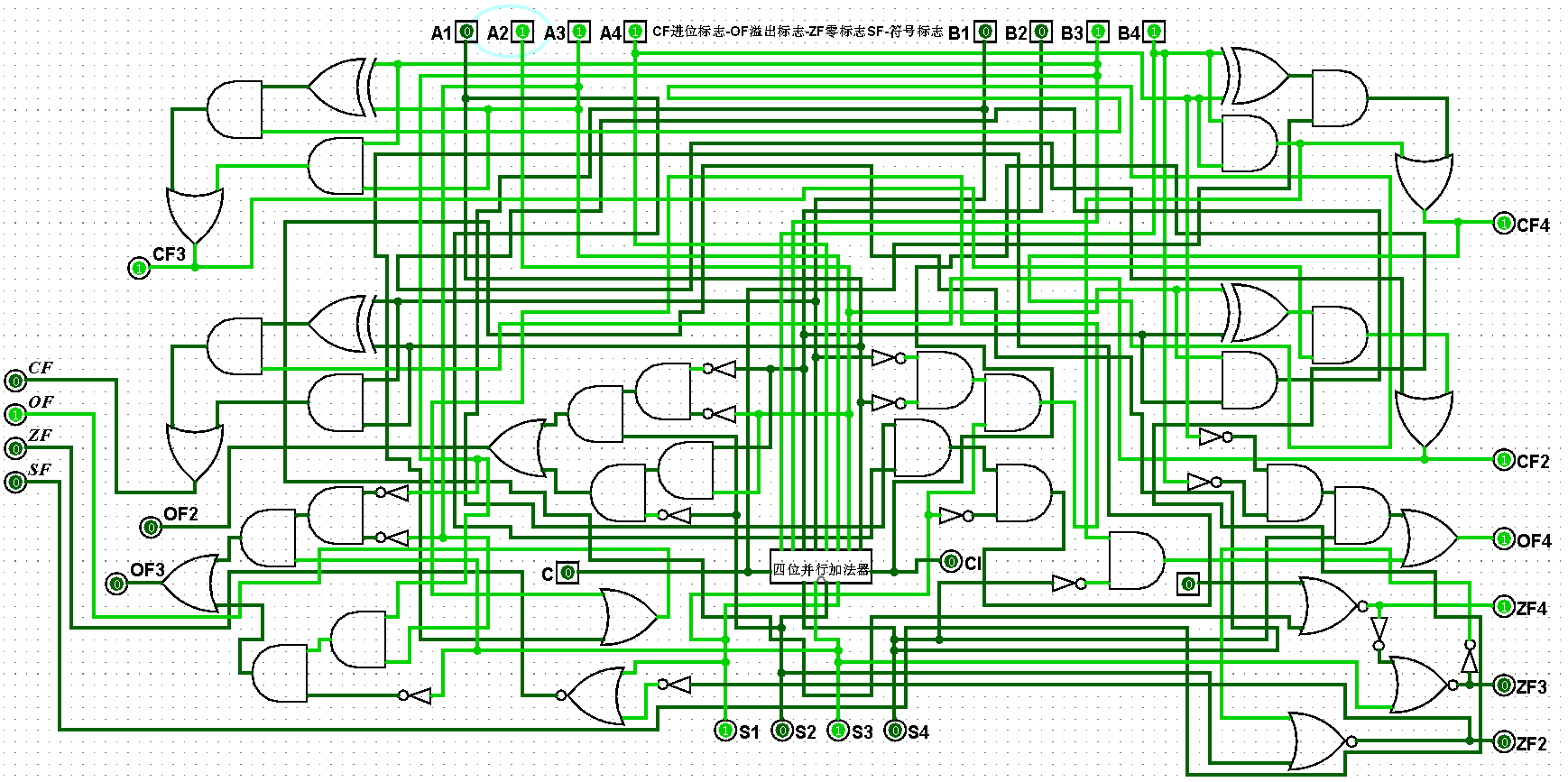
图5-2-7 四位二进制运算器测试7+3=10,CF=0,OF=1,ZF=0,SF=0
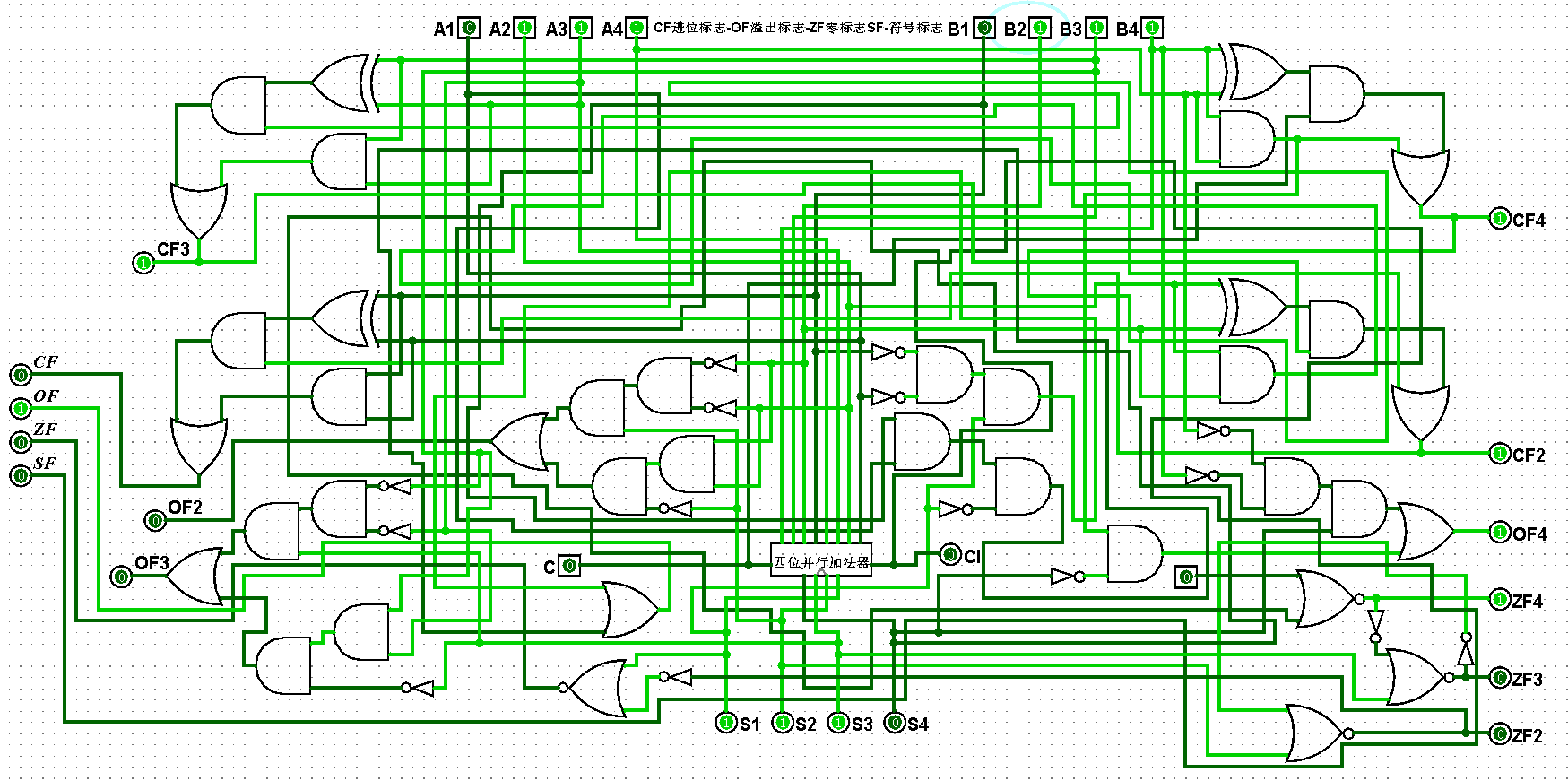
图5-2-8 四位二进制运算器测试7+7=14,CF=0,OF=1,ZF=0,SF=0
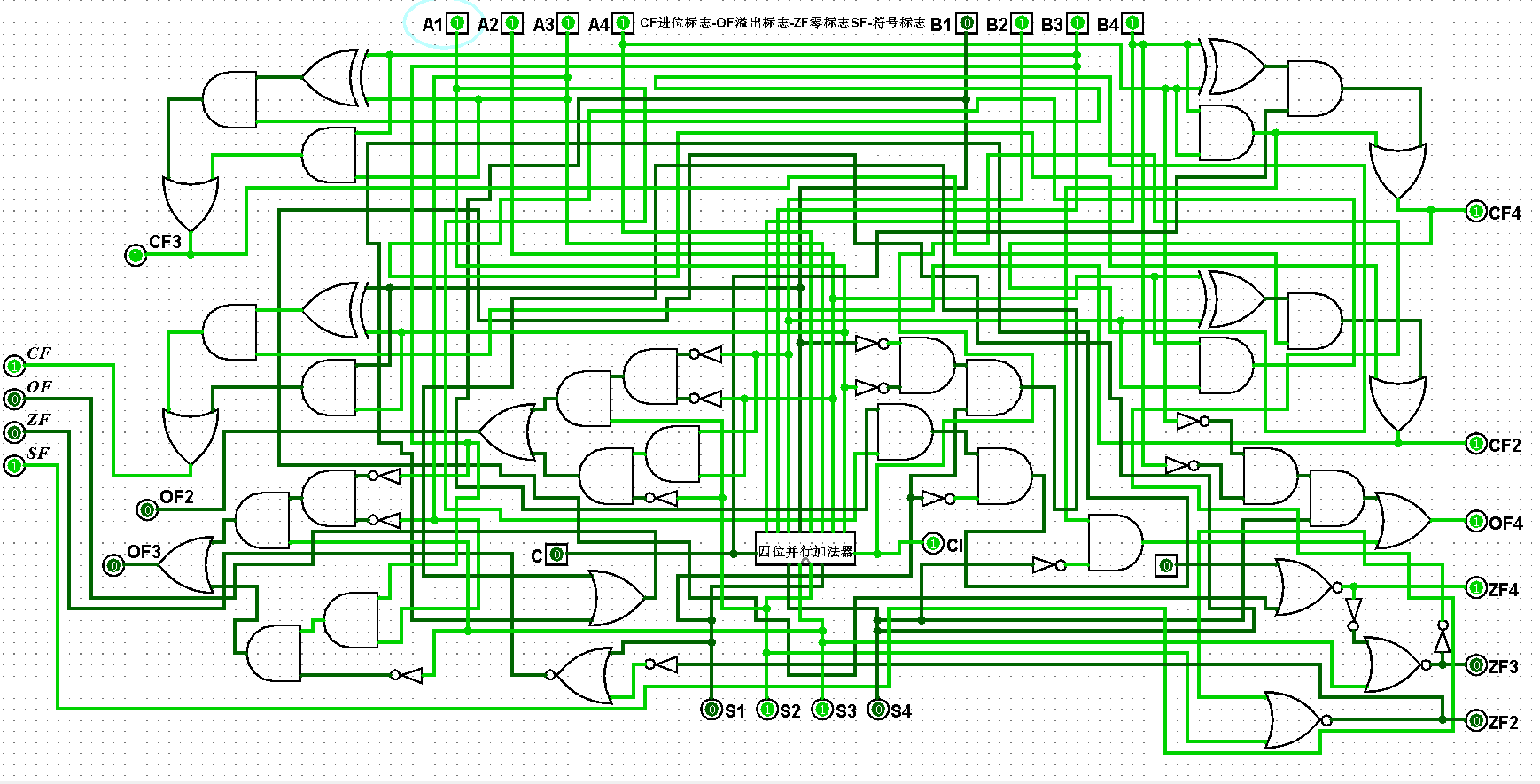
图5-2-9 四位二进制运算器测试15+7=22,CF=1,OF=0,ZF=0,SF=1
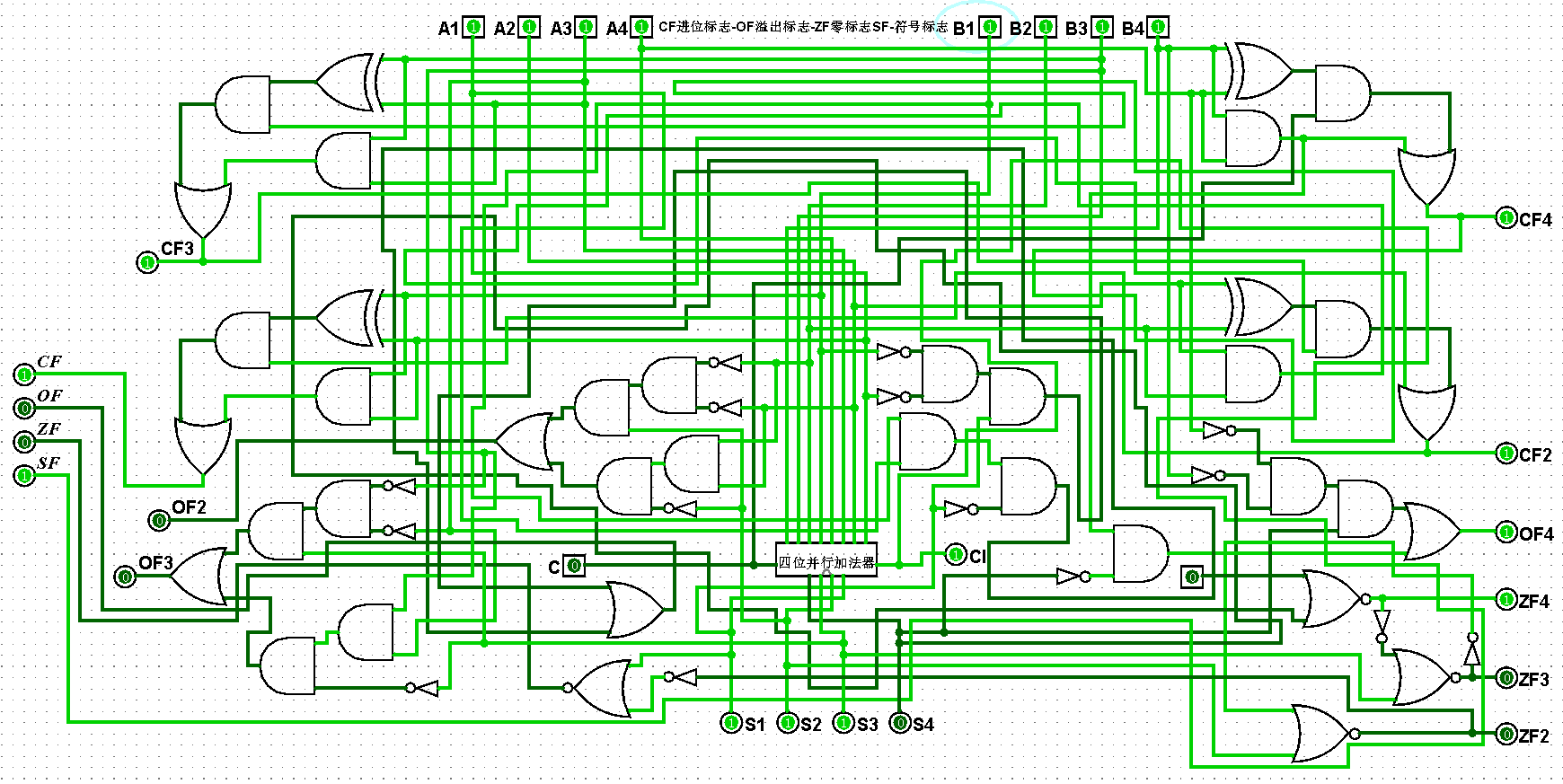
图5-2-10 四位二进制运算器测试15+15=30,CF=1,OF=0,ZF=0,SF=1
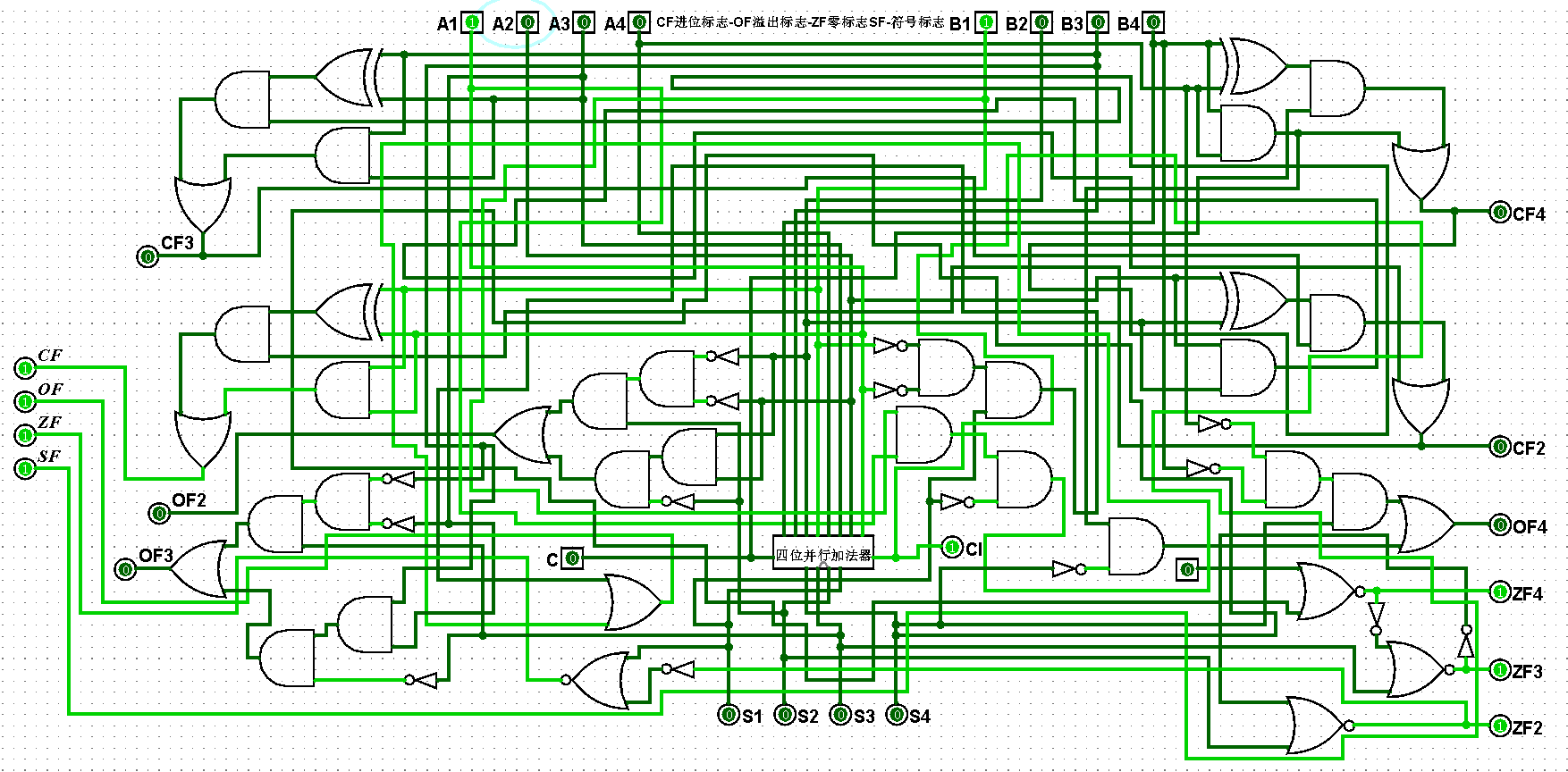
图5-2-11 四位二进制运算器测试8+8=16,CF=1,OF=1,ZF=1,SF=1
3、打开Logisim软件,利用两个四位二进制加法器实现八位串行加法器,列出八位串行加法器逻辑电路真值表,并使用两个四位二进制加法器实现八位串行加法器逻辑电路,铺设完成后进行测试进而判断电路是否铺设成功。
(1)通过低位的高位进位是高位的低位进位的方式搭建八位串行加法器,将低位的高位进位输入到高位的低位进位上实现八位串行加法器的逻辑电路,对应的部分八位串行加法器逻辑电路真值表如图5-3-1所示:
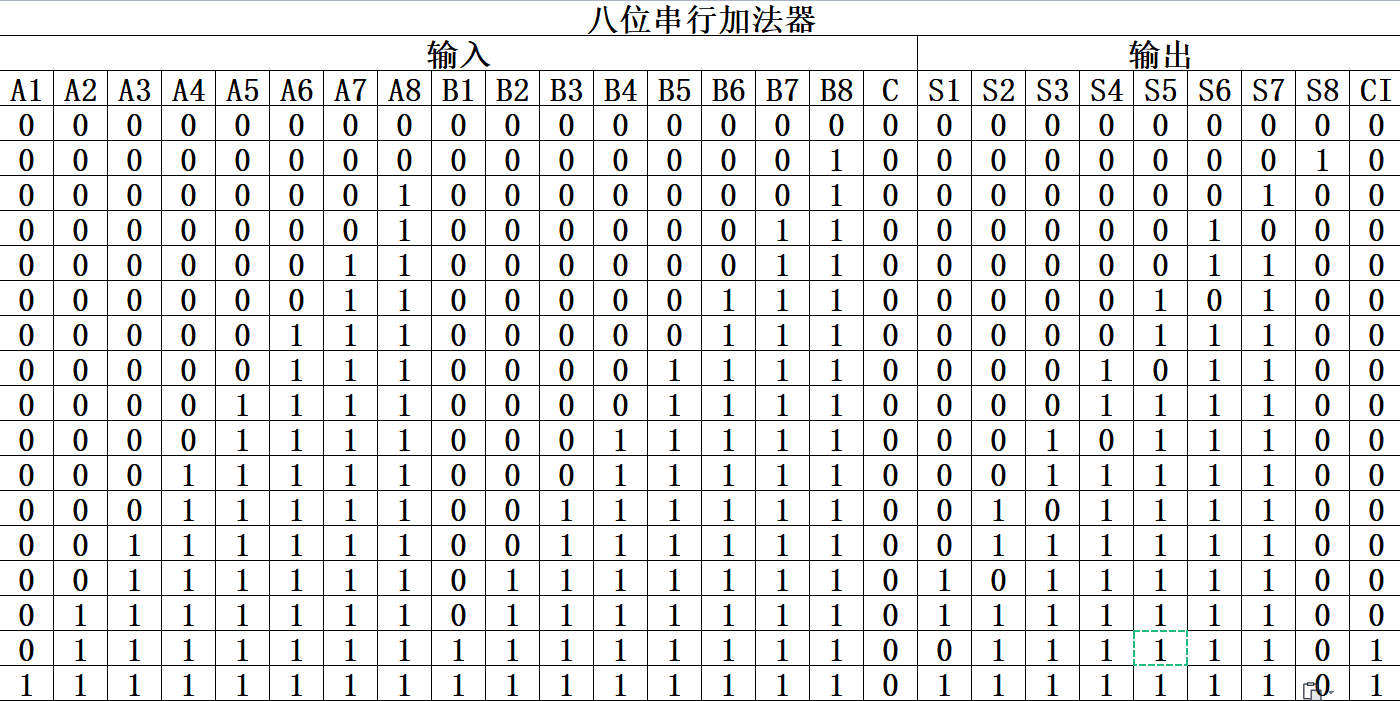
图5-3-1 八位串行加法器逻辑电路真值表
(2)依据逻辑原理完成八位串行加法器逻辑电路的架构,在运行过程中低位的高位进位是高位的低位进位,将对应的进位进行构连即可实现八位串行加法器,对应的八位串行加法器逻辑电路如图5-3-2至5-3-18所示:
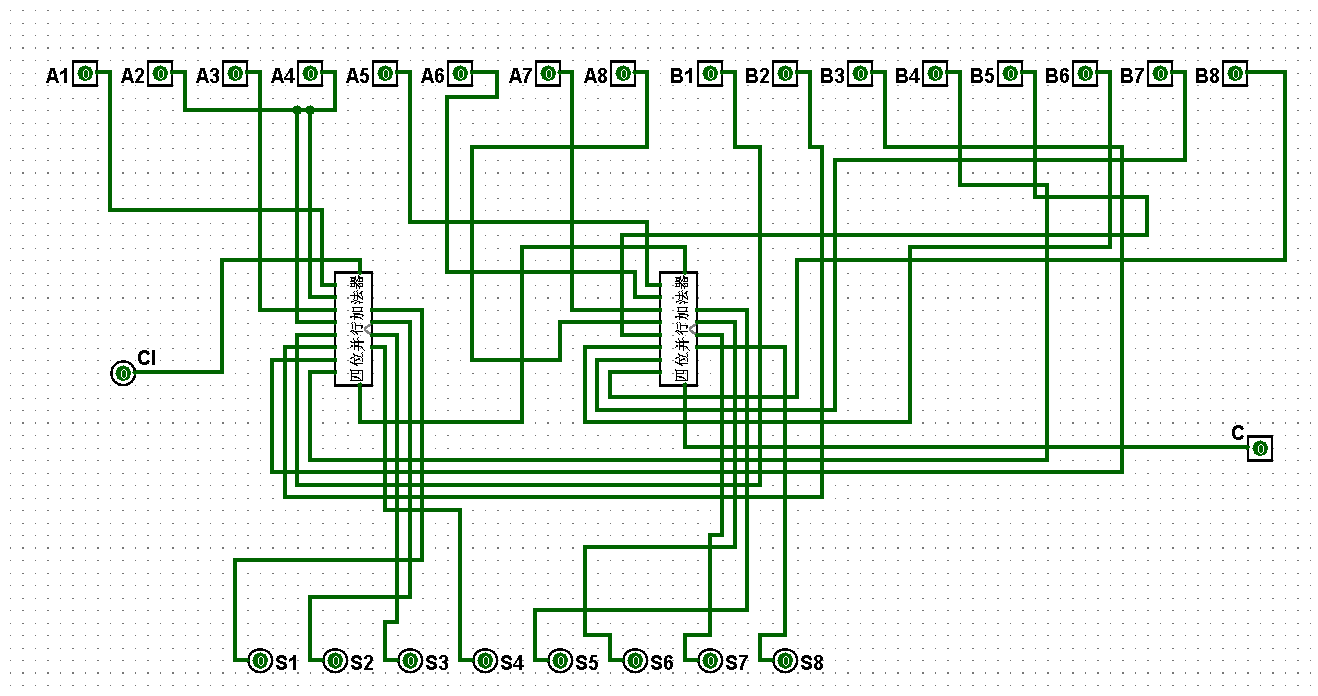
图5-3-2 八位串行加法器逻辑电路
(3)八位串行加法器逻辑电路铺设完毕后进行测试,进而判断自己的电路是否铺设成功,经过测试后此电路状态一切正常,对应的八位串行加法器逻辑电路测试如图5-3-3至5-3-18所示:
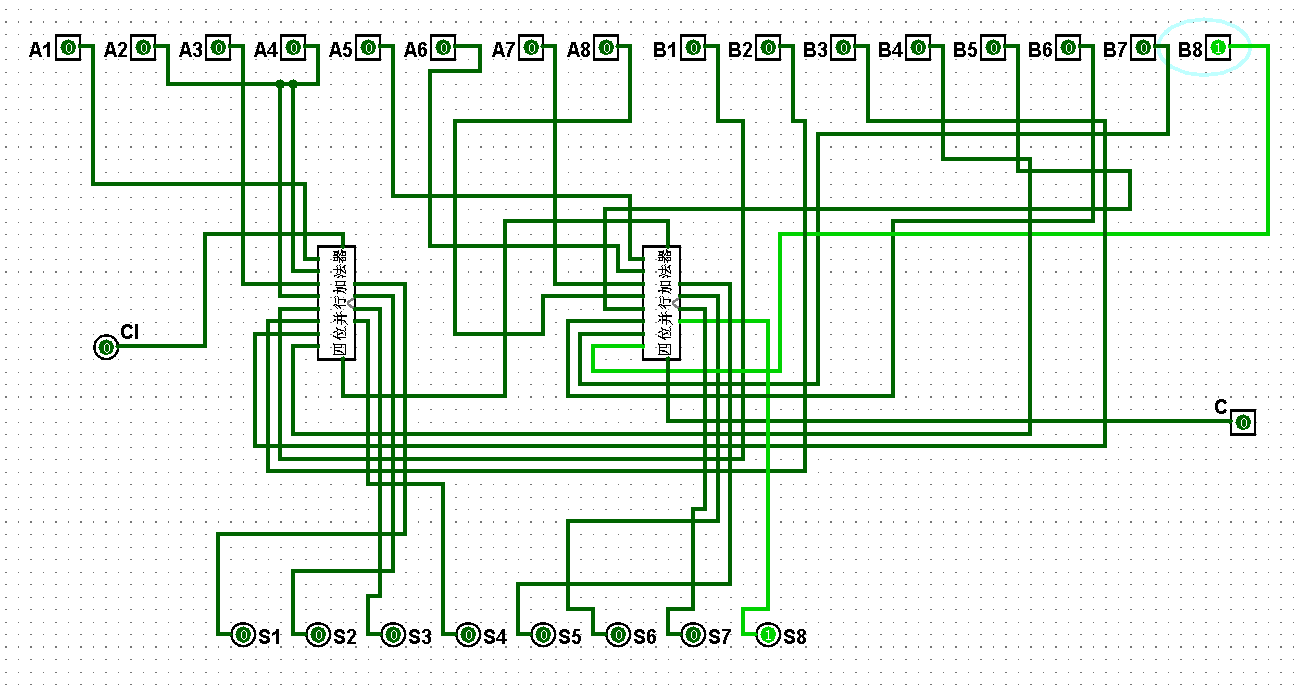
图5-3-3 八位串行加法器测试0+1=1
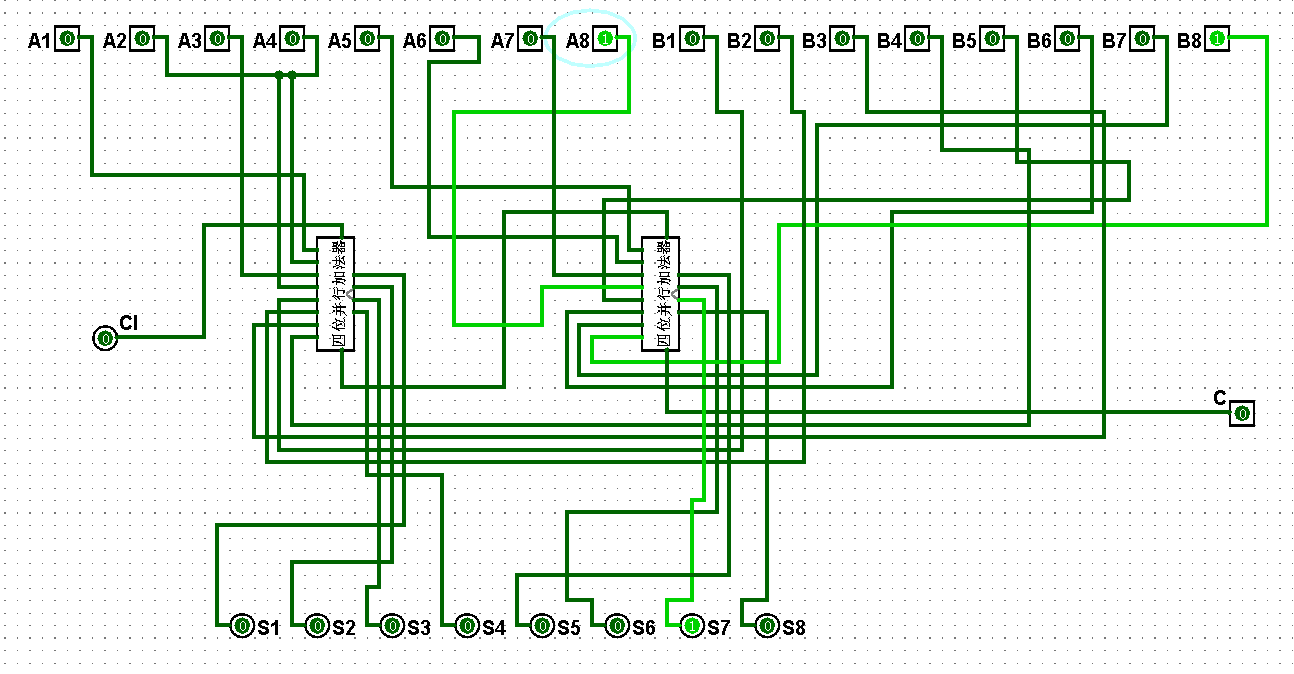
图5-3-4 八位串行加法器测试1+1=2
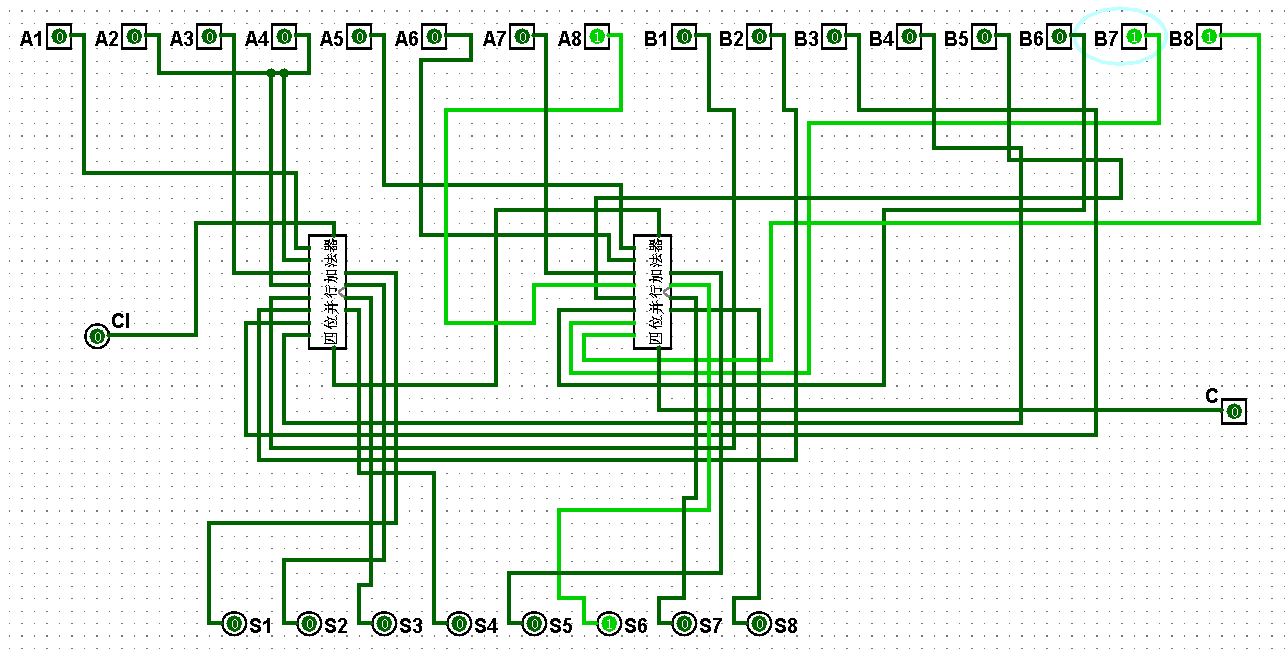
图5-3-5 八位串行加法器测试1+3=4
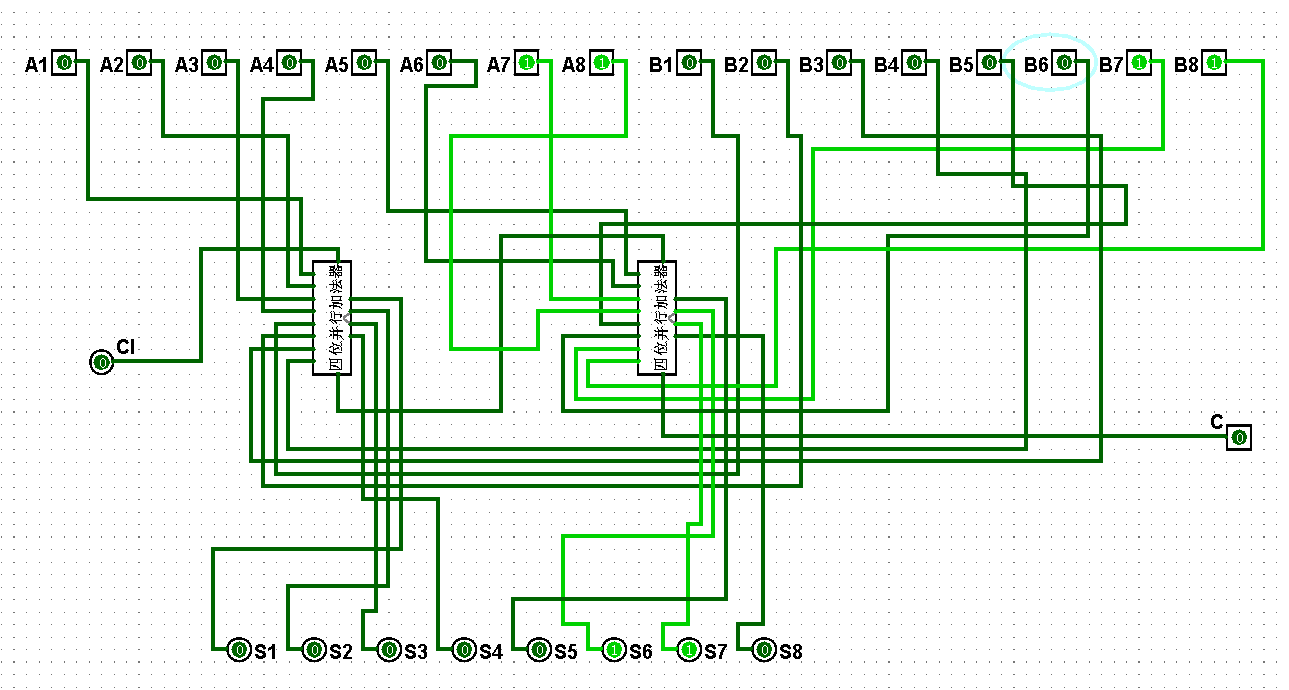
图5-3-6 八位串行加法器测试3+3=6
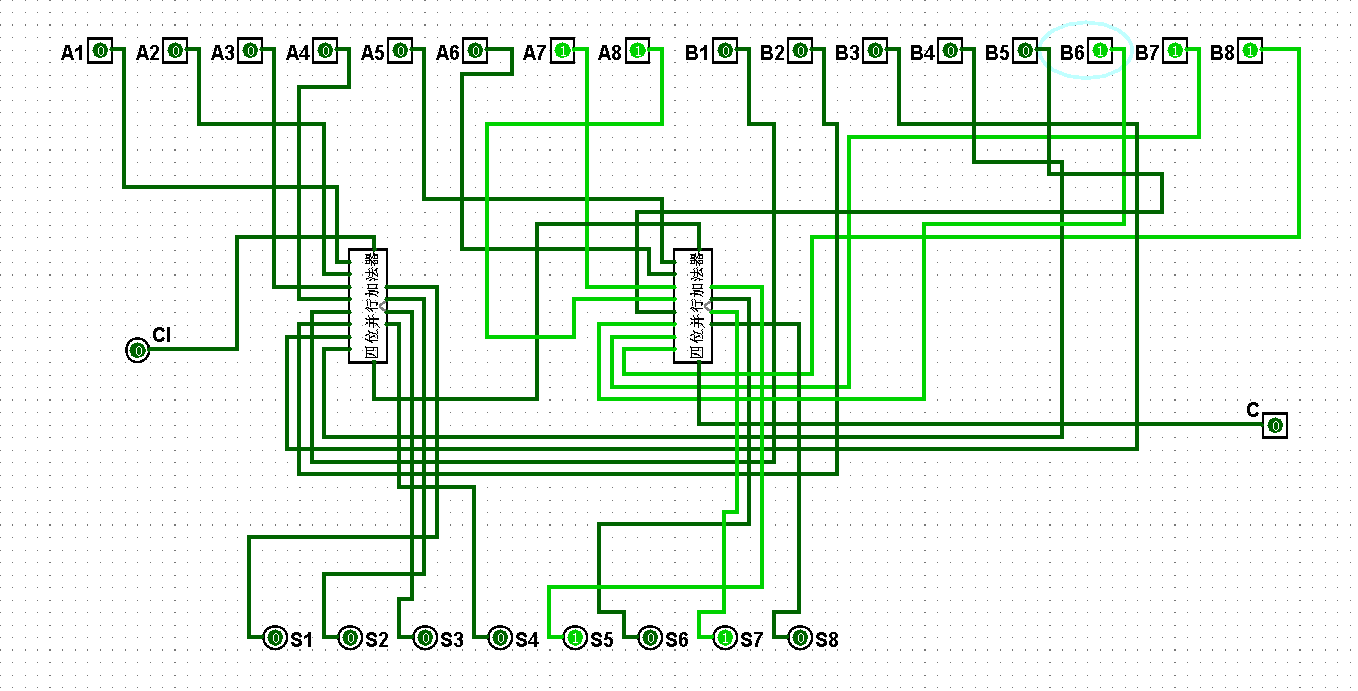
图5-3-7 八位串行加法器测试3+7=10
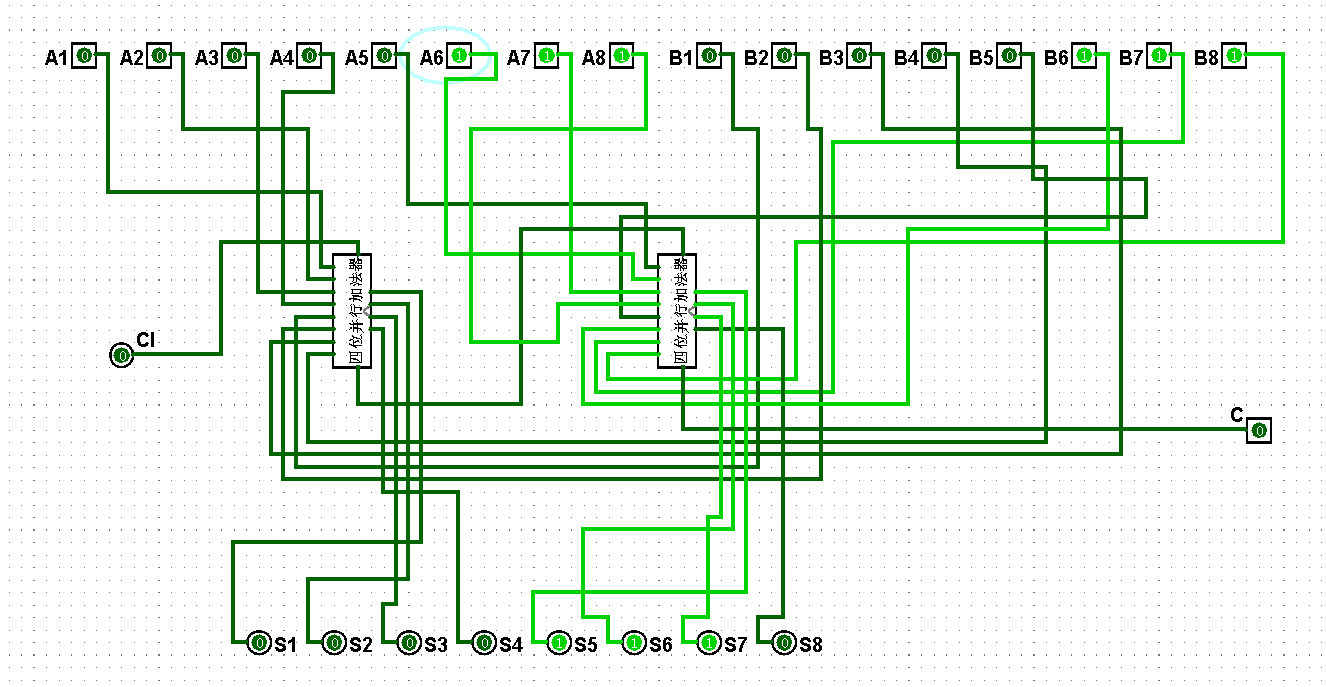
图5-3-8 八位串行加法器测试7+7=14
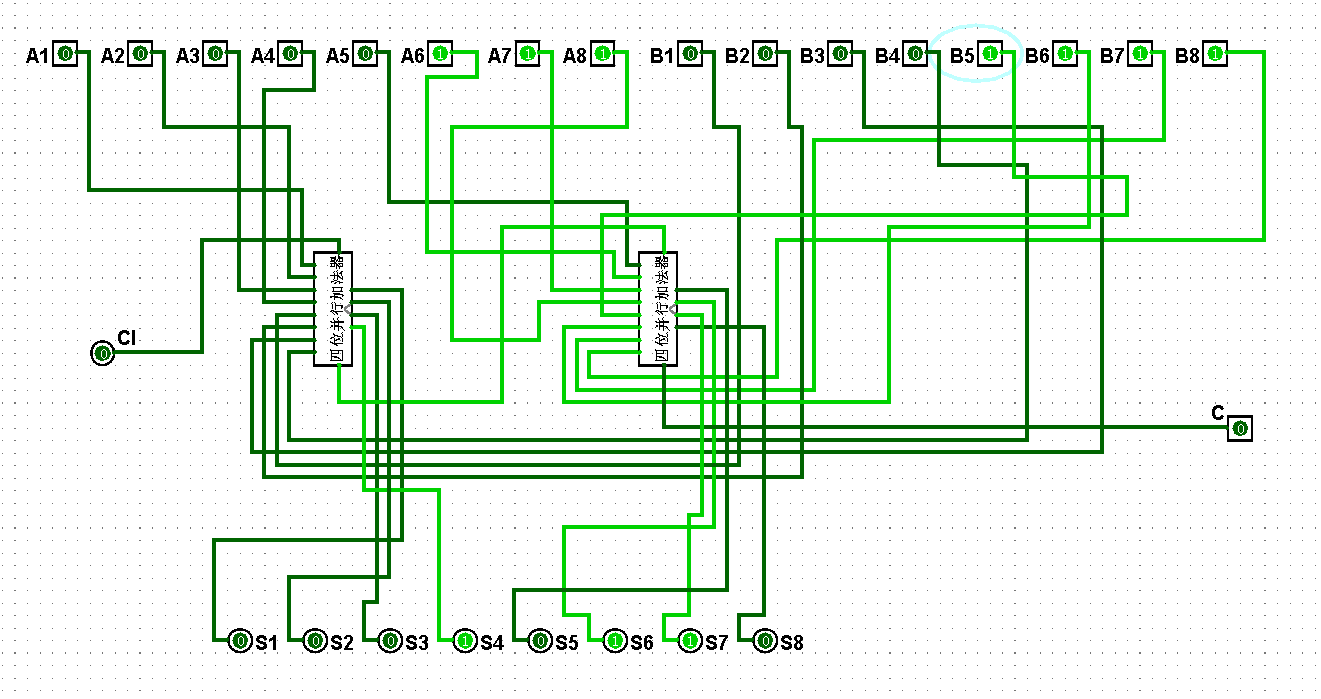
图5-3-9 八位串行加法器测试7+15=22
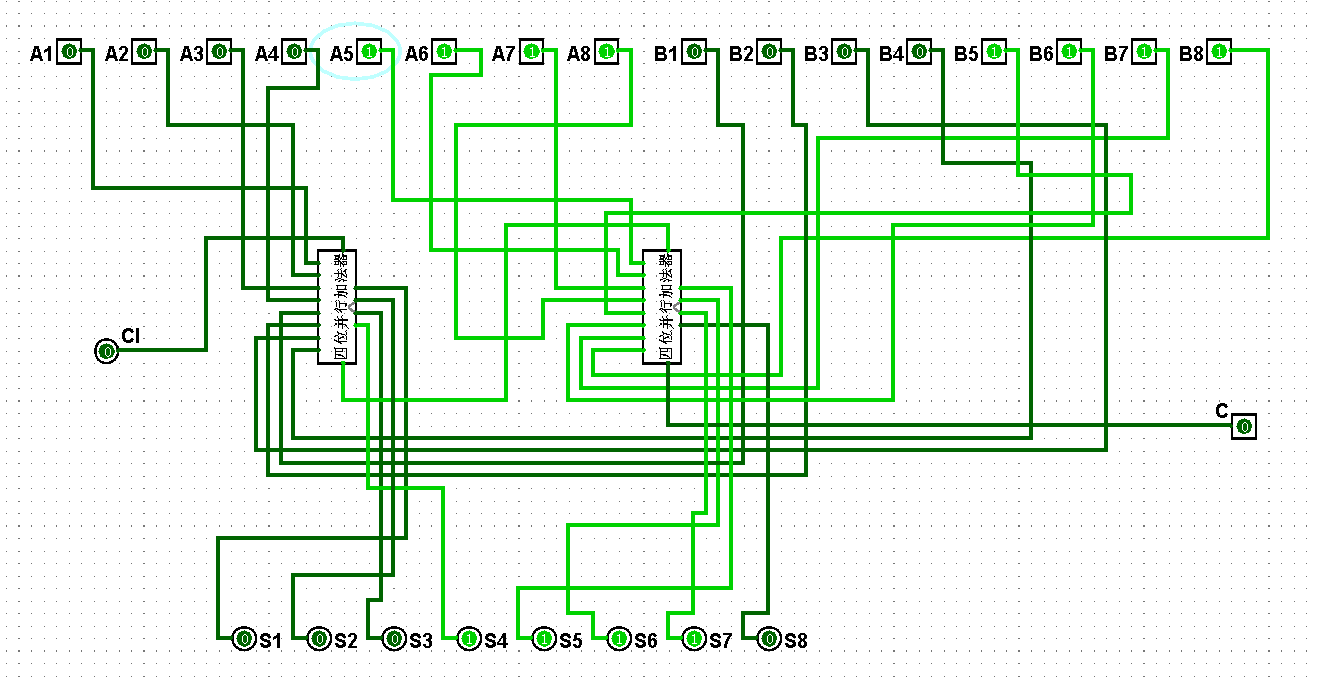
图5-3-10 八位串行加法器测试15+15=30
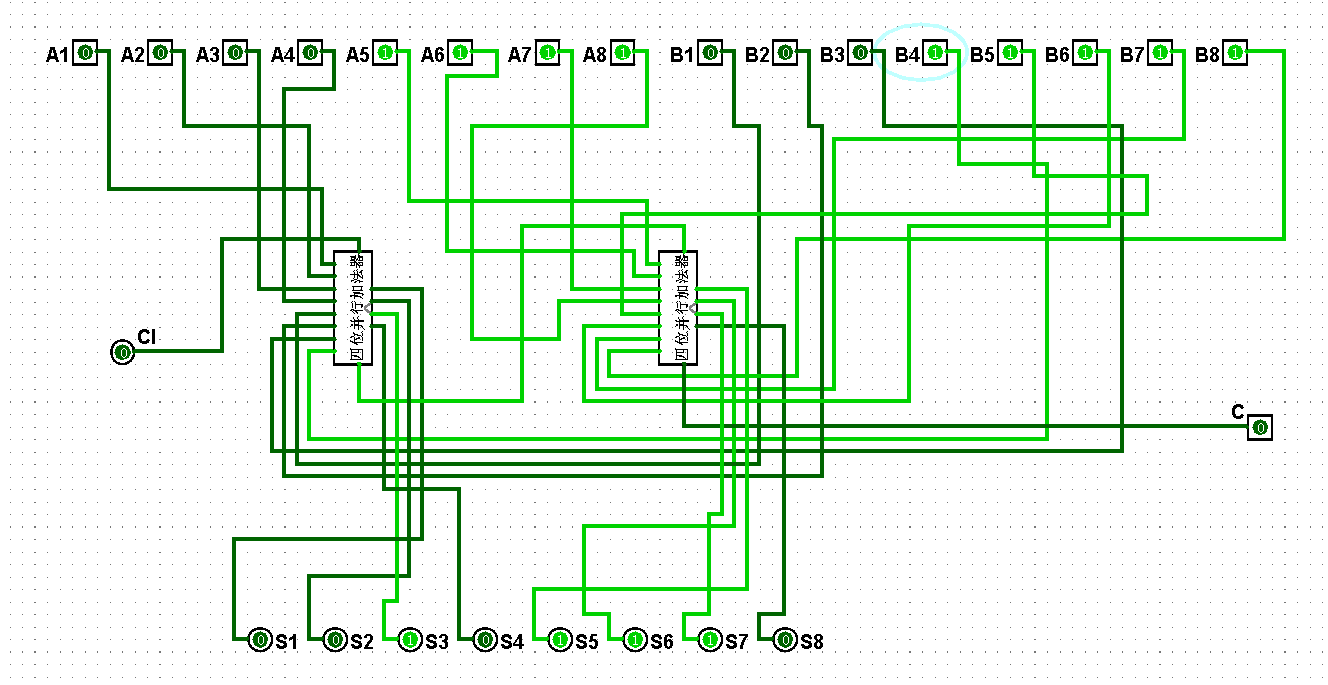
图5-3-11 八位串行加法器测试15+31=46
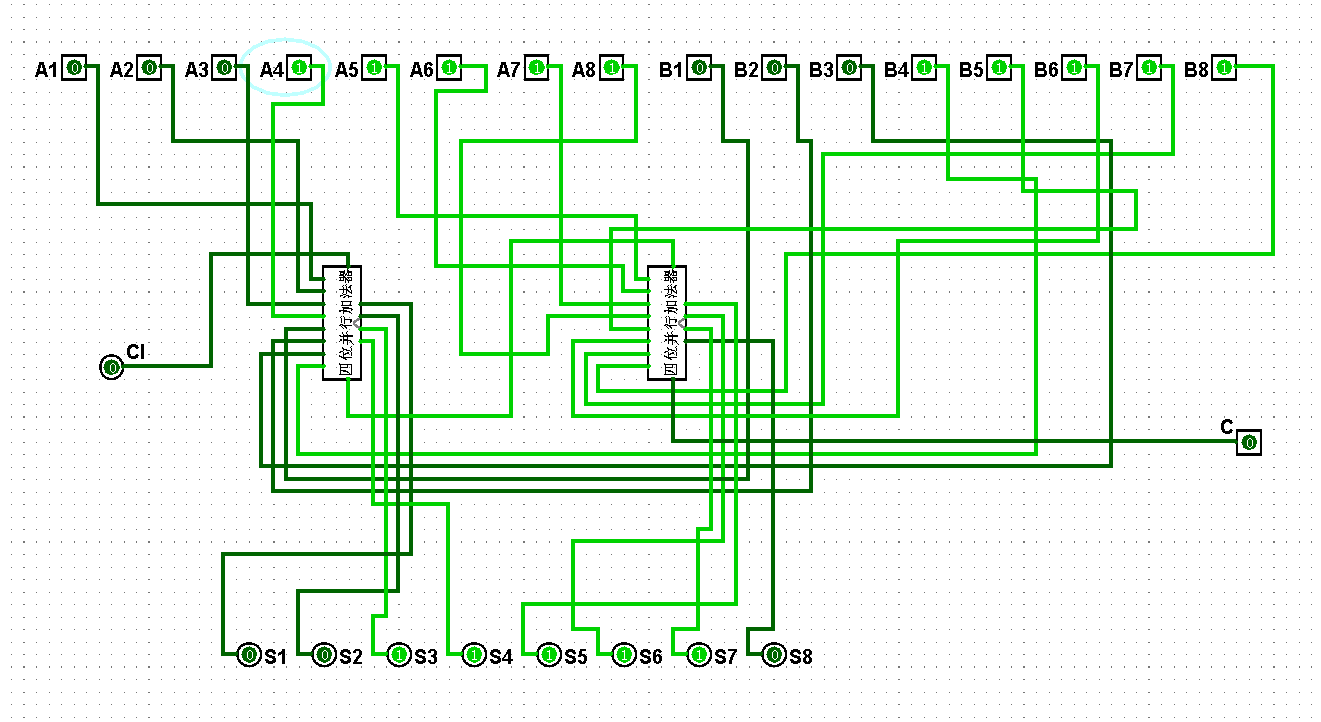
图5-3-12 八位串行加法器测试31+31=62
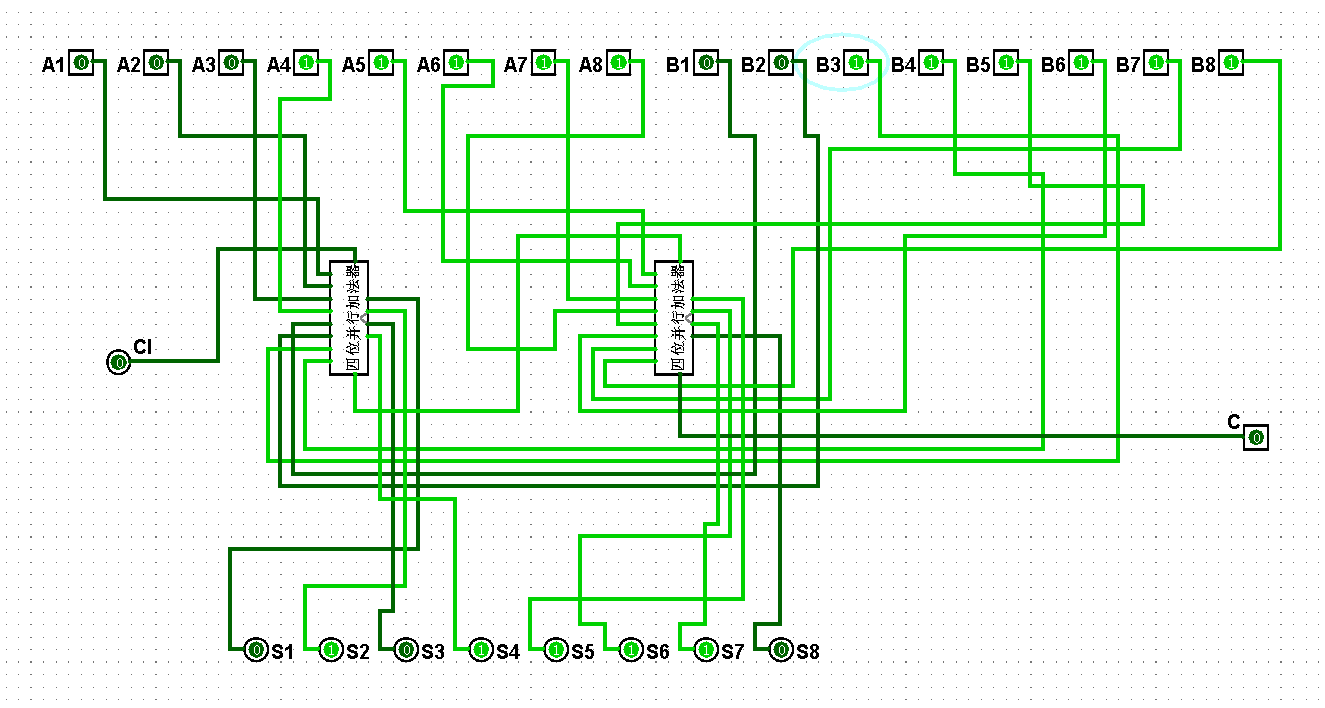
图5-3-13 八位串行加法器测试31+63=94
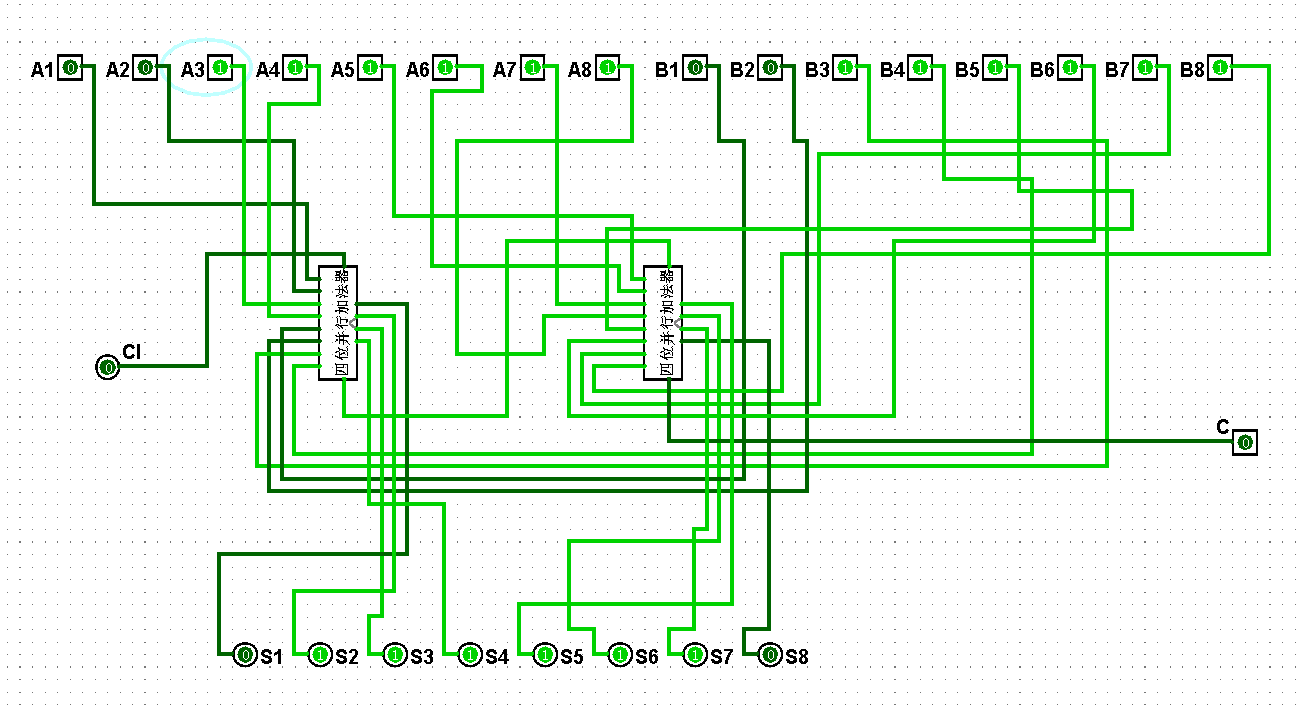
图5-3-14 八位串行加法器测试63+63=126
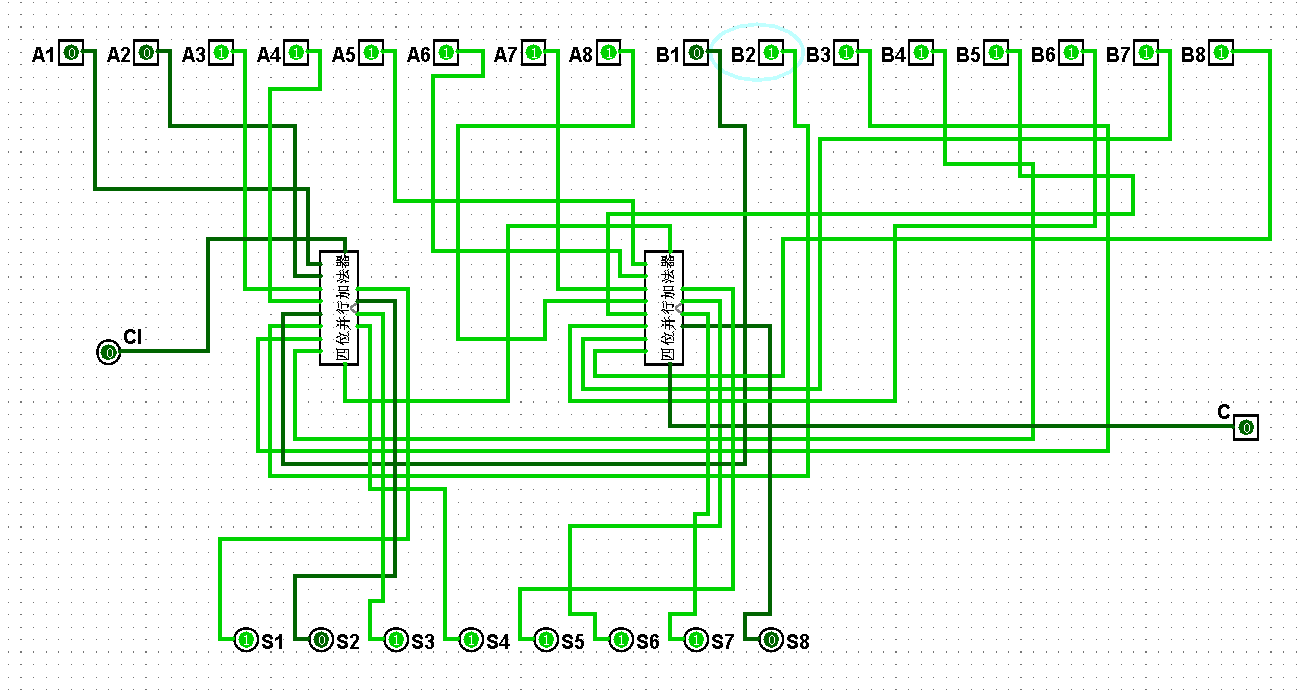
图5-3-15 八位串行加法器测试63+127=190
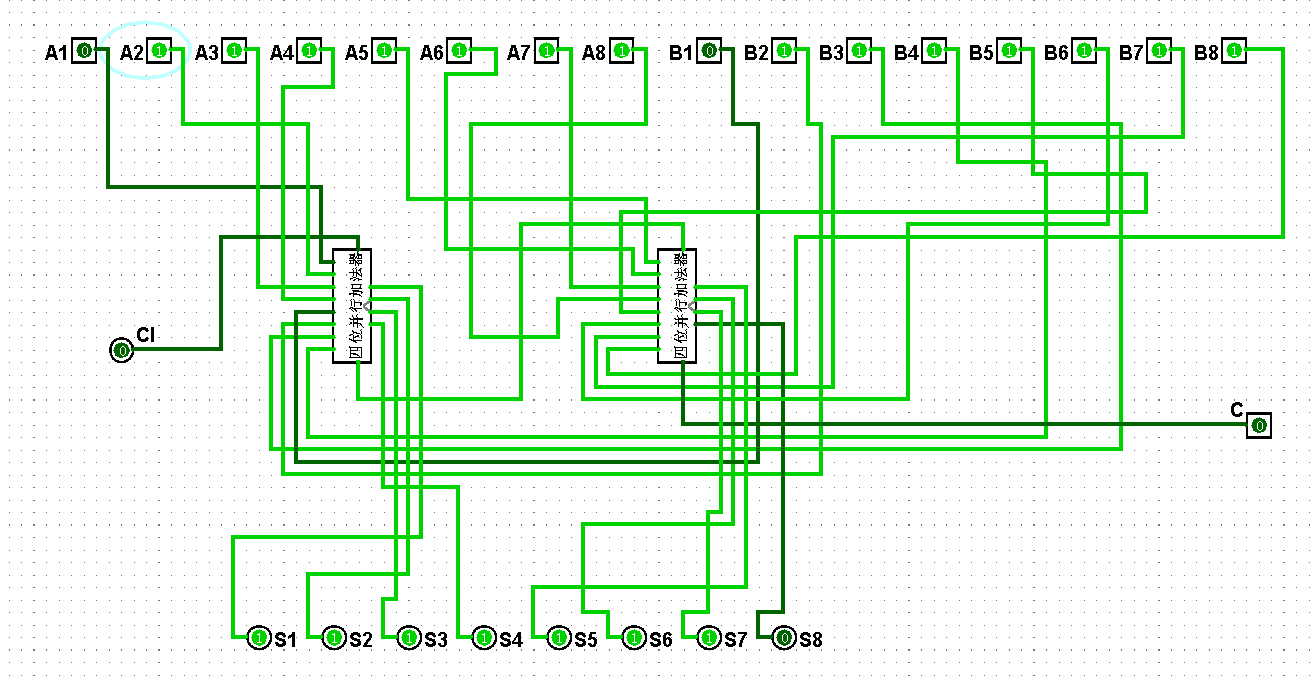
图5-3-16 八位串行加法器测试127+127=254
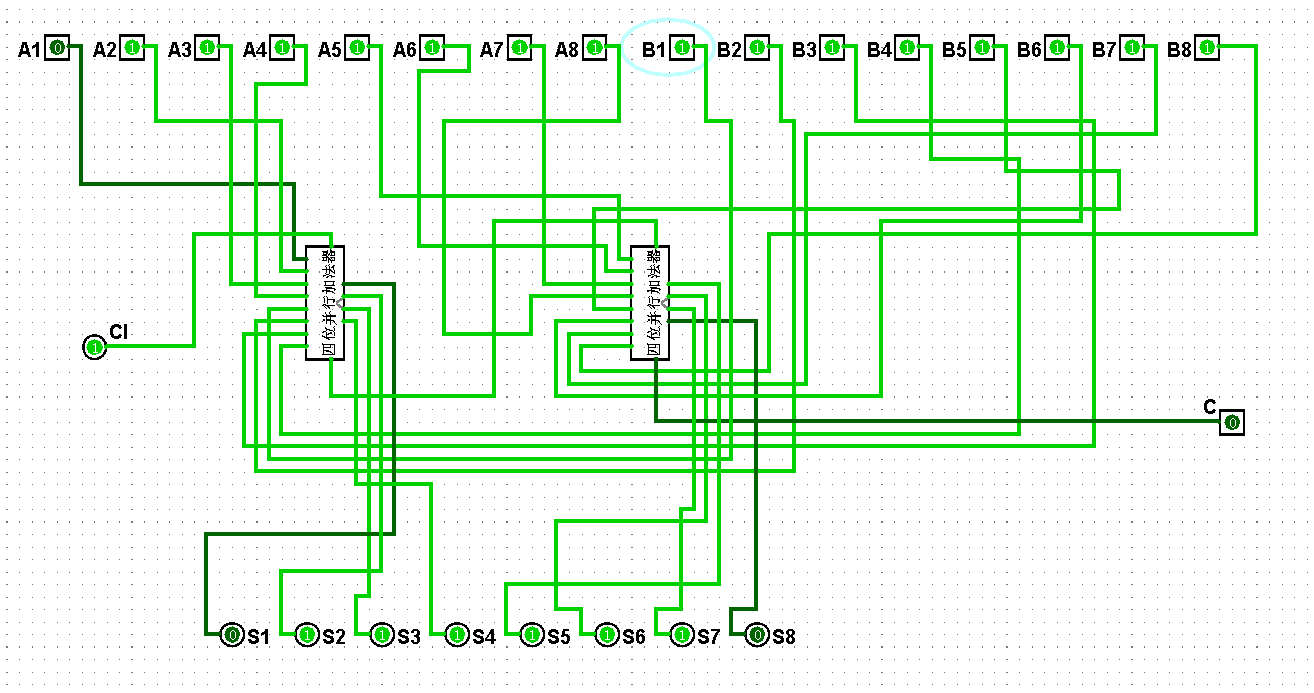
图5-3-17 八位串行加法器测试127+255=382
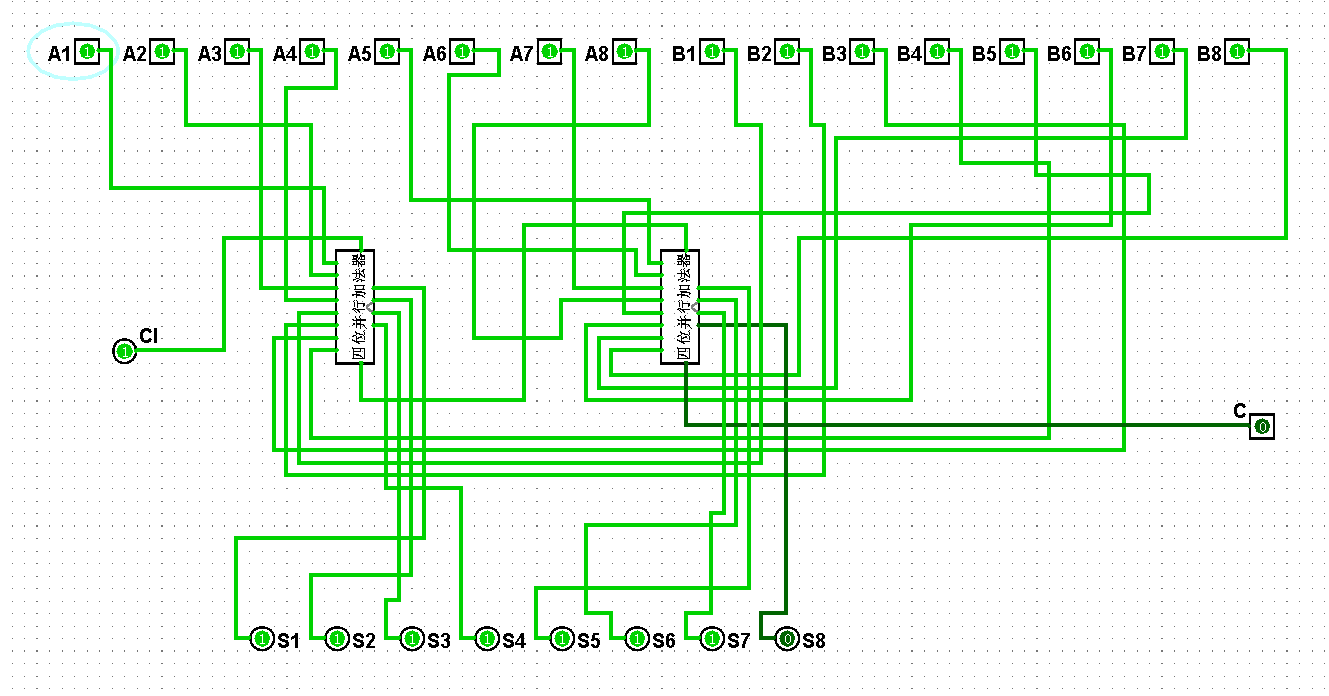
图5-3-18 八位串行加法器测试255+255=510
4、打开Logisim软件,利用两个四位二进制加法器实现八位并行加法器,列出八位并行加法器逻辑电路真值表,并使用两个四位二进制加法器实现八位并行加法器逻辑电路,铺设完成后进行测试进而判断电路是否铺设成功。
(1)通过同时共享各位进位的方式搭建八位并行加法器,将低位的高位进位结果得到后进入高位的低位进位,进而使两个四位二进制加法器同时处于工作状态,实现八位并行加法器的逻辑电路,对应的部分八位并行加法器逻辑电路真值表如图5-4-1所示:
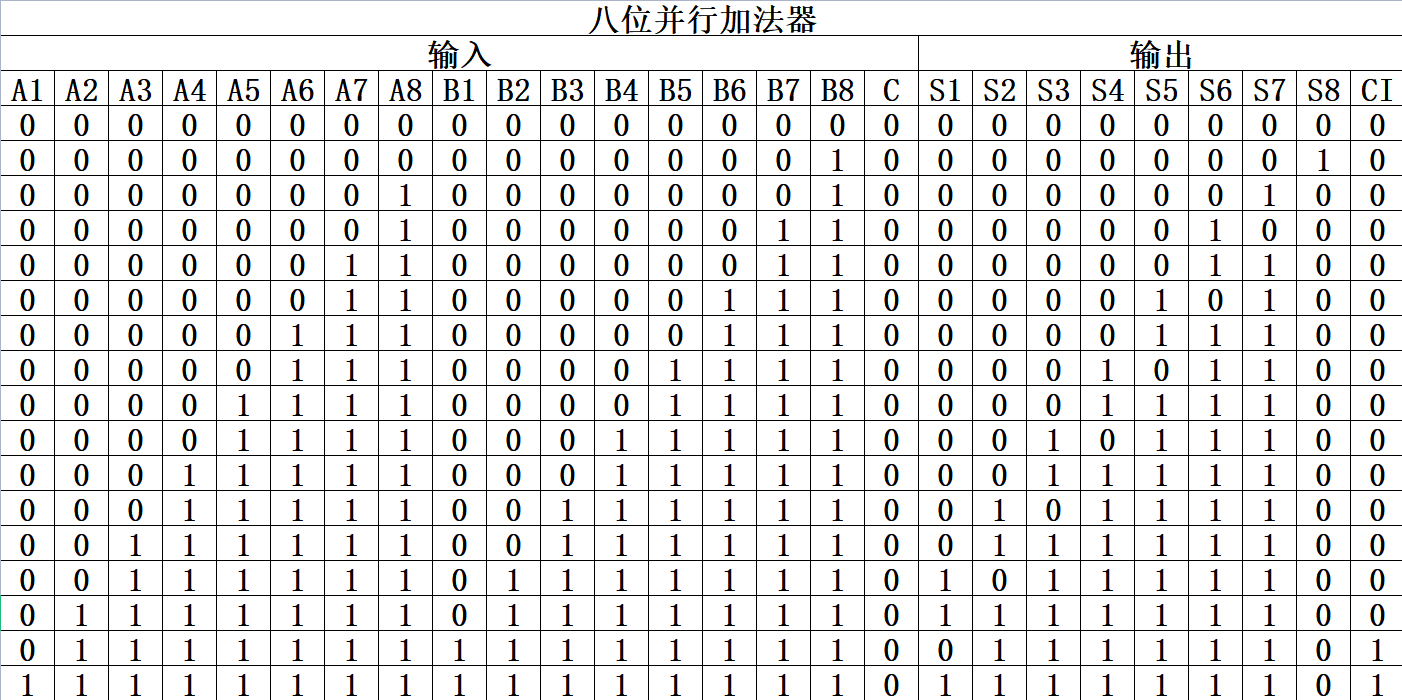
图5-4-1 八位并行加法器逻辑电路真值表
(2)依据逻辑原理完成八位并行加法器逻辑电路的架构,在运行过程中将低位的高位进位结果共享到各个高位的低位进位上,将对应的进位进行构连即可实现八位并行加法器,对应的八位并行加法器逻辑电路如图5-4-2至5-4-18所示:
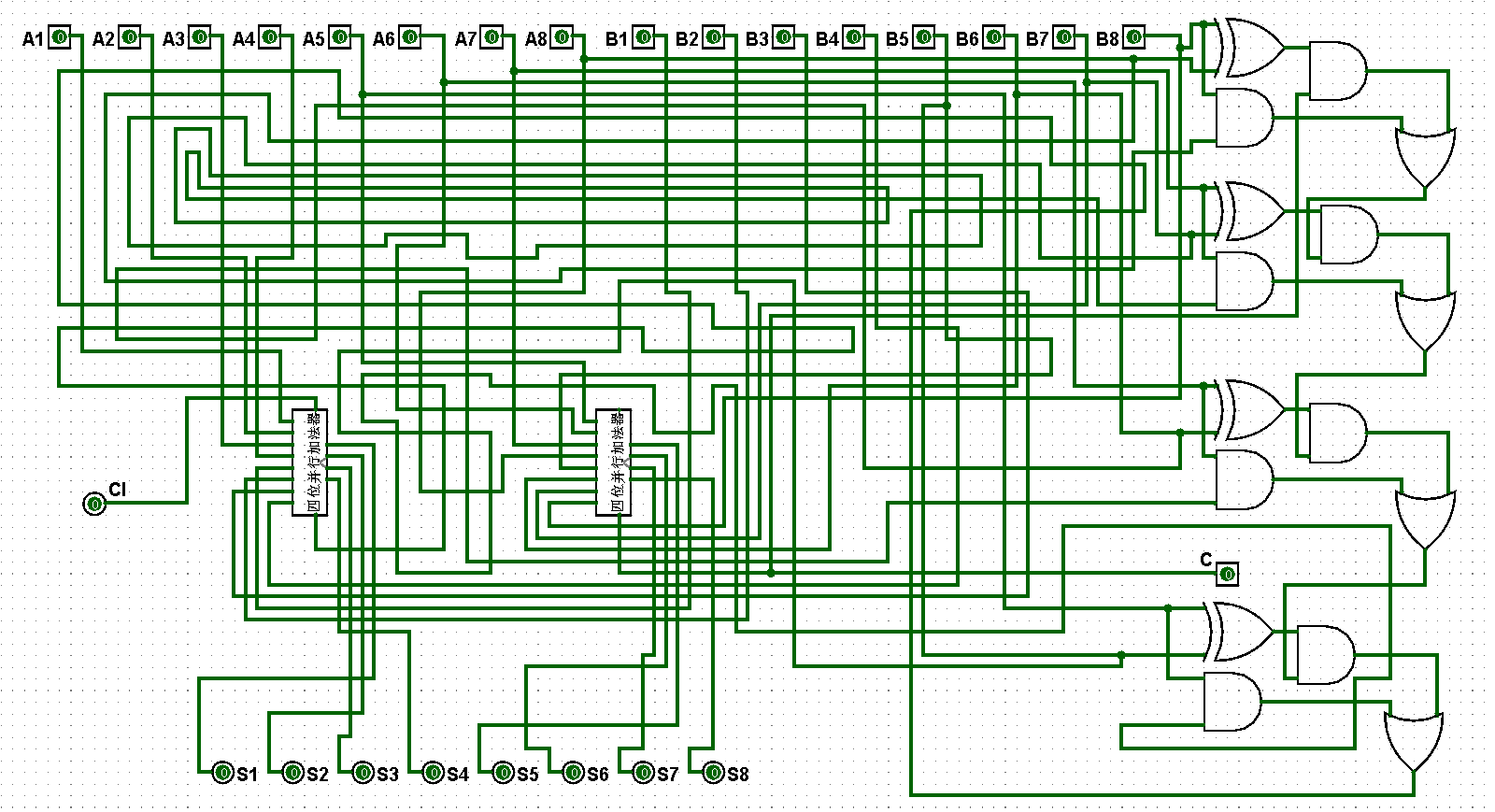
图5-4-2 八位并行加法器逻辑电路
(3)八位并行加法器逻辑电路铺设完毕后进行测试,进而判断自己的电路是否铺设成功,经过测试后此电路状态一切正常,对应的八位并行加法器逻辑电路测试如图5-4-3至5-4-18所示:
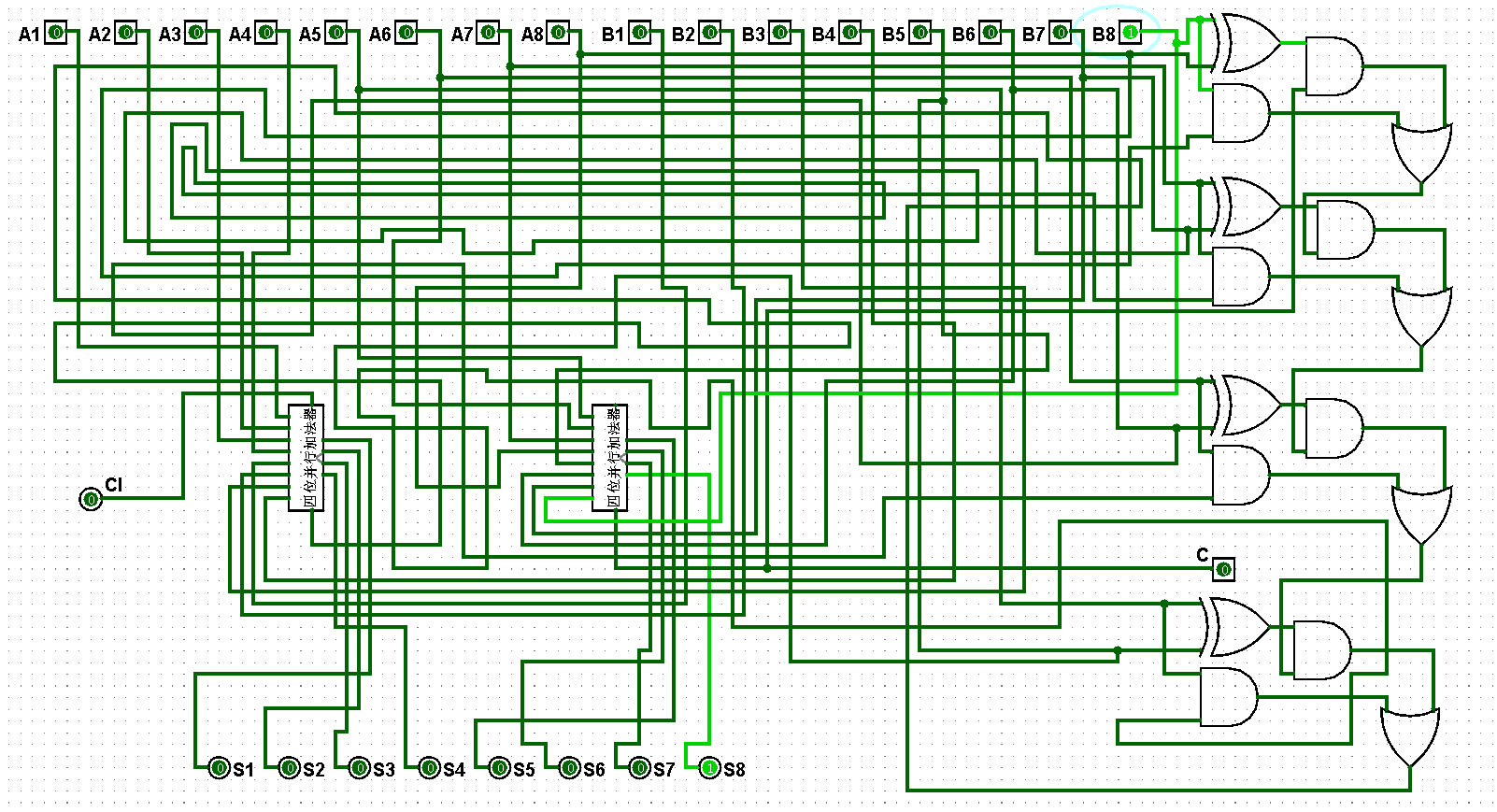
图5-3-3 八位并行加法器测试0+1=1
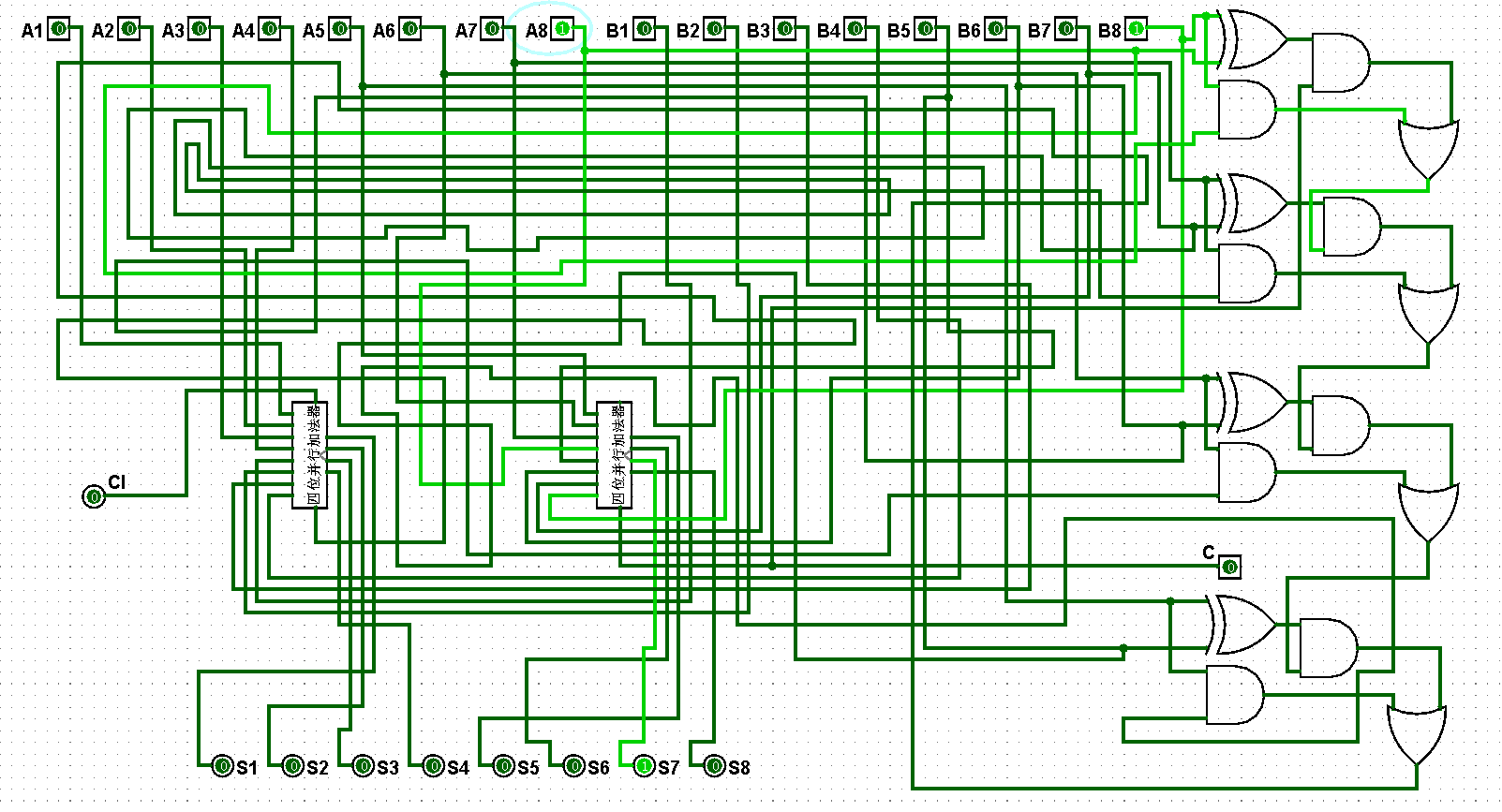
图5-3-4 八位并行加法器测试1+1=2
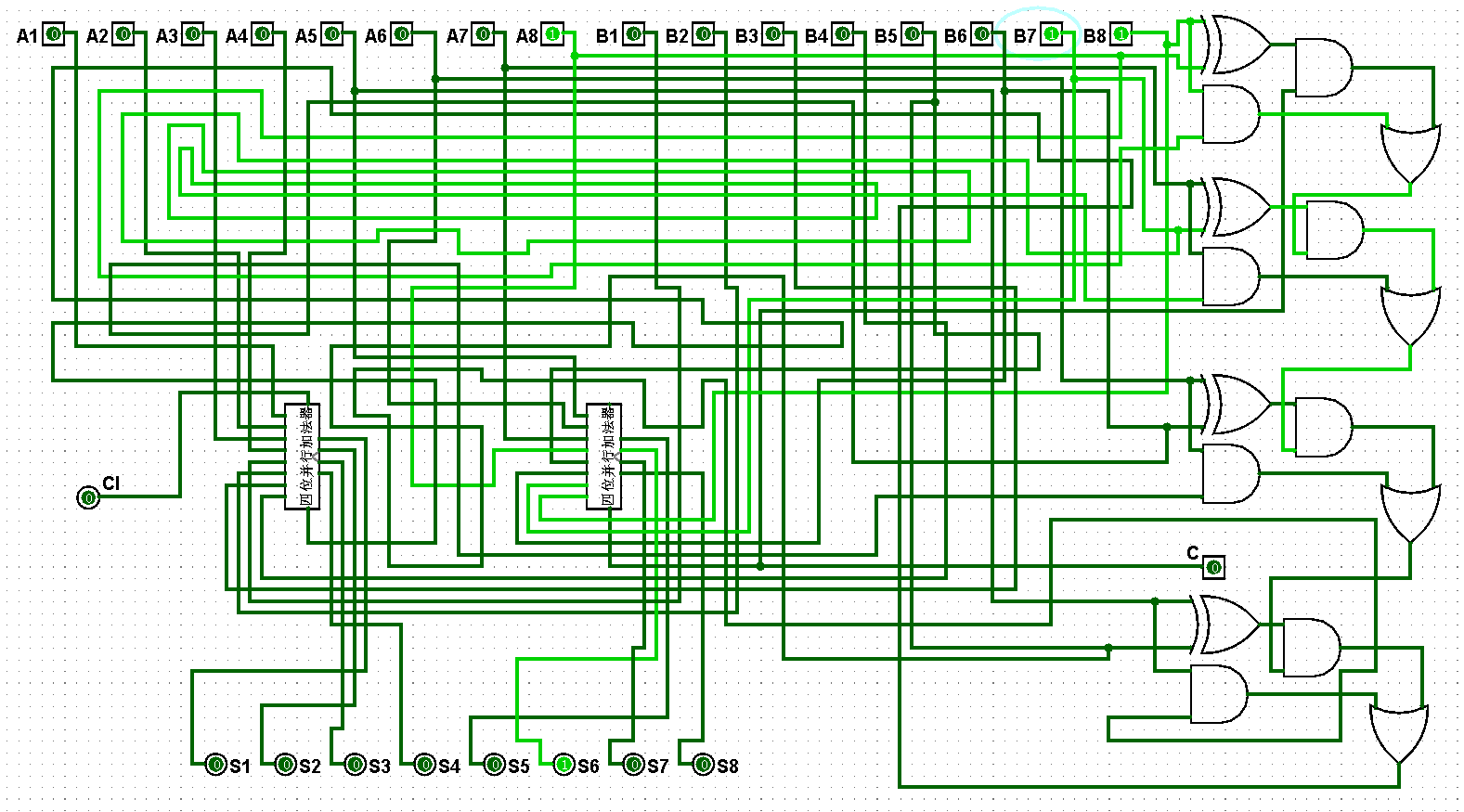
图5-3-5 八位并行加法器测试1+3=4
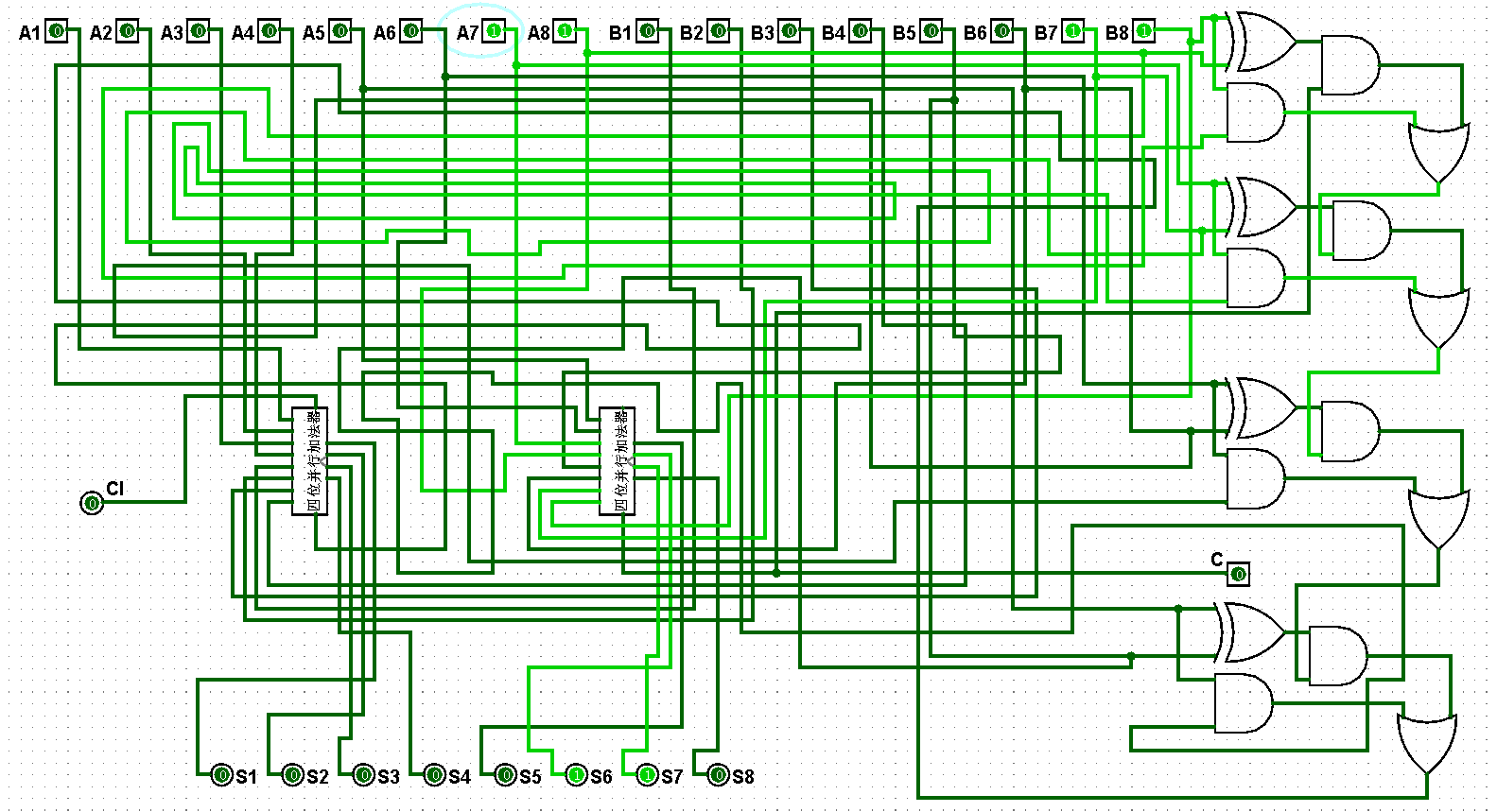
图5-3-6 八位并行加法器测试3+3=6
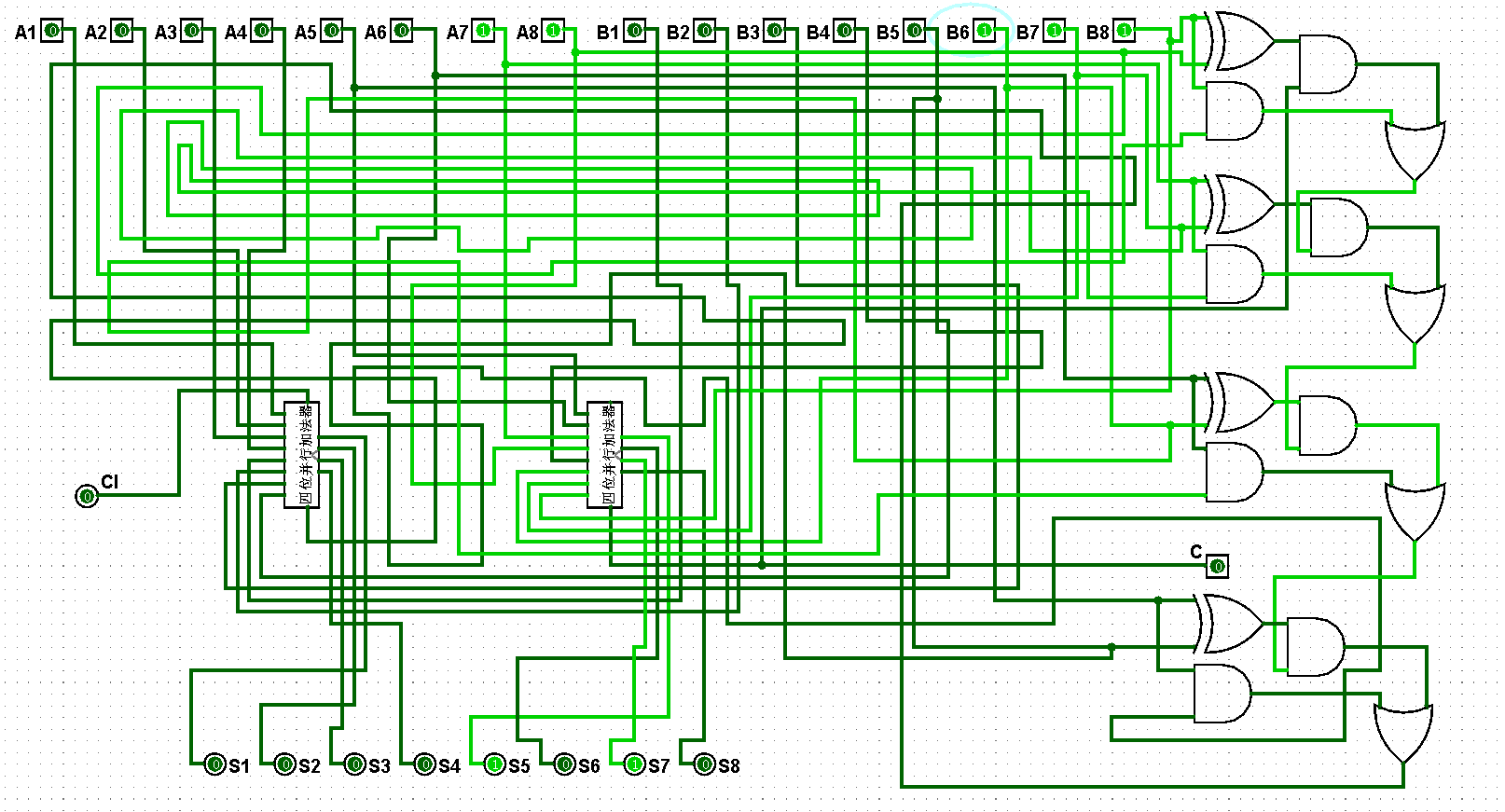
图5-3-7 八位并行加法器测试3+7=10
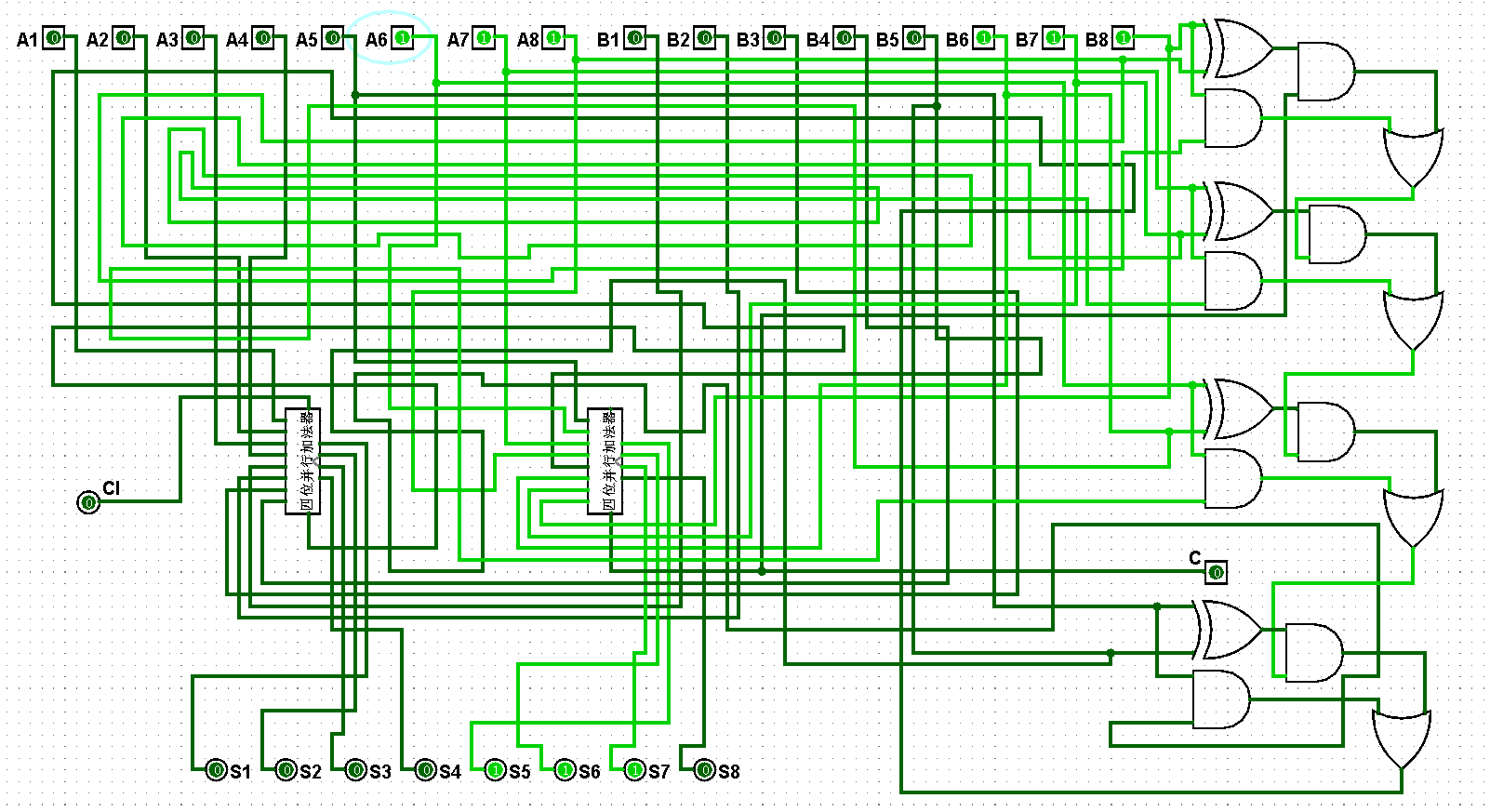
图5-3-8 八位并行加法器测试7+7=14
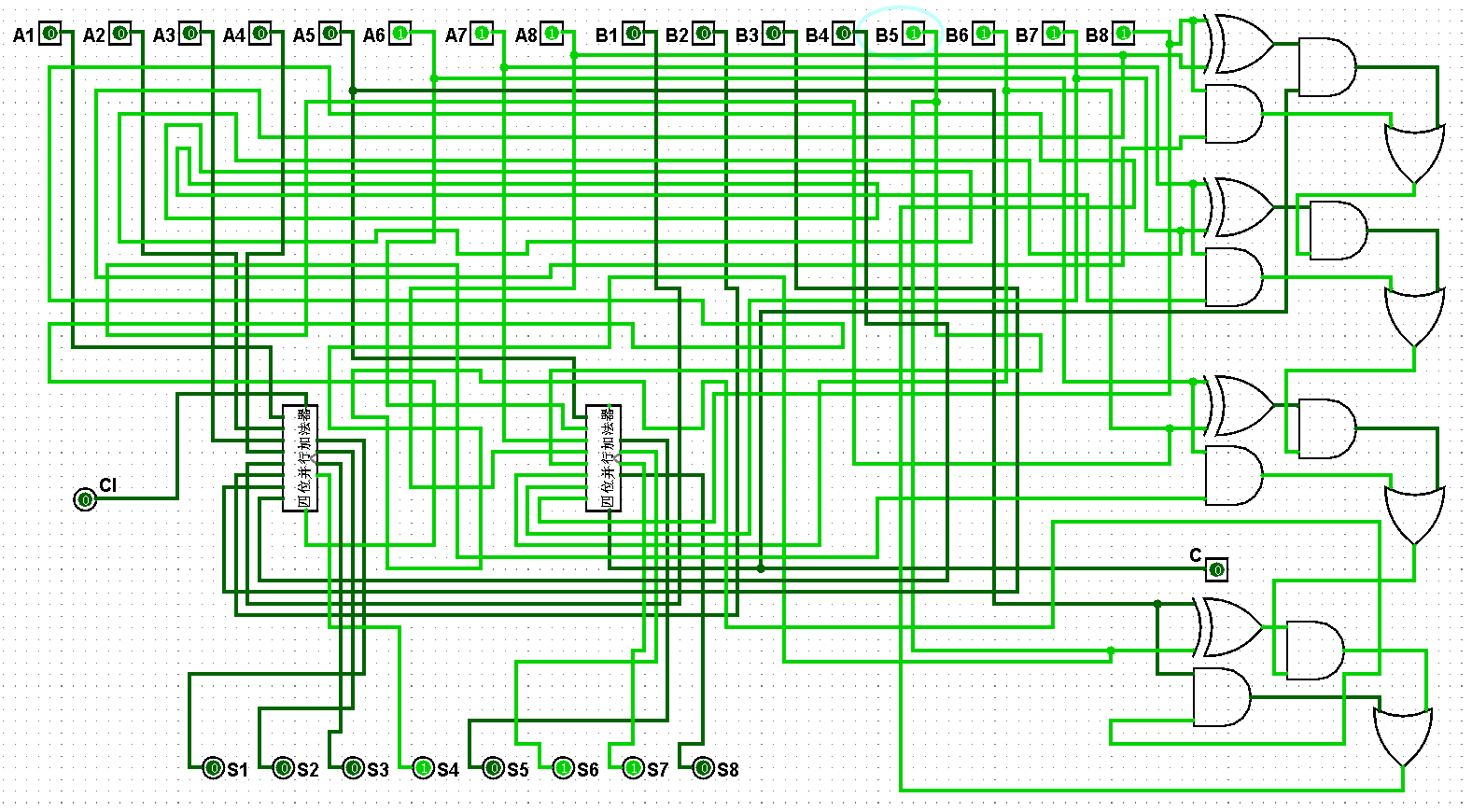
图5-3-9 八位并行加法器测试7+15=22
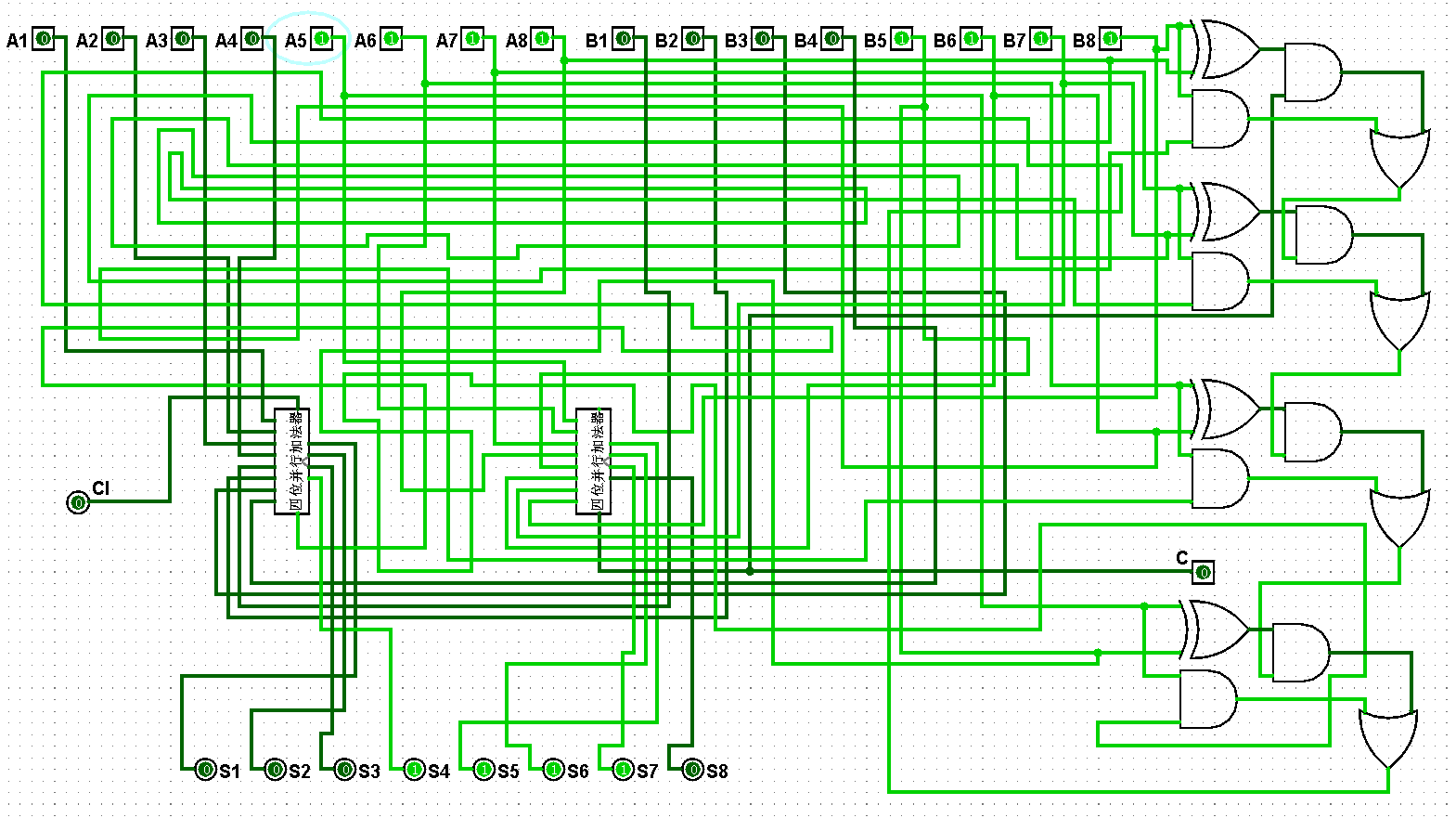
图5-3-10 八位并行加法器测试15+15=30
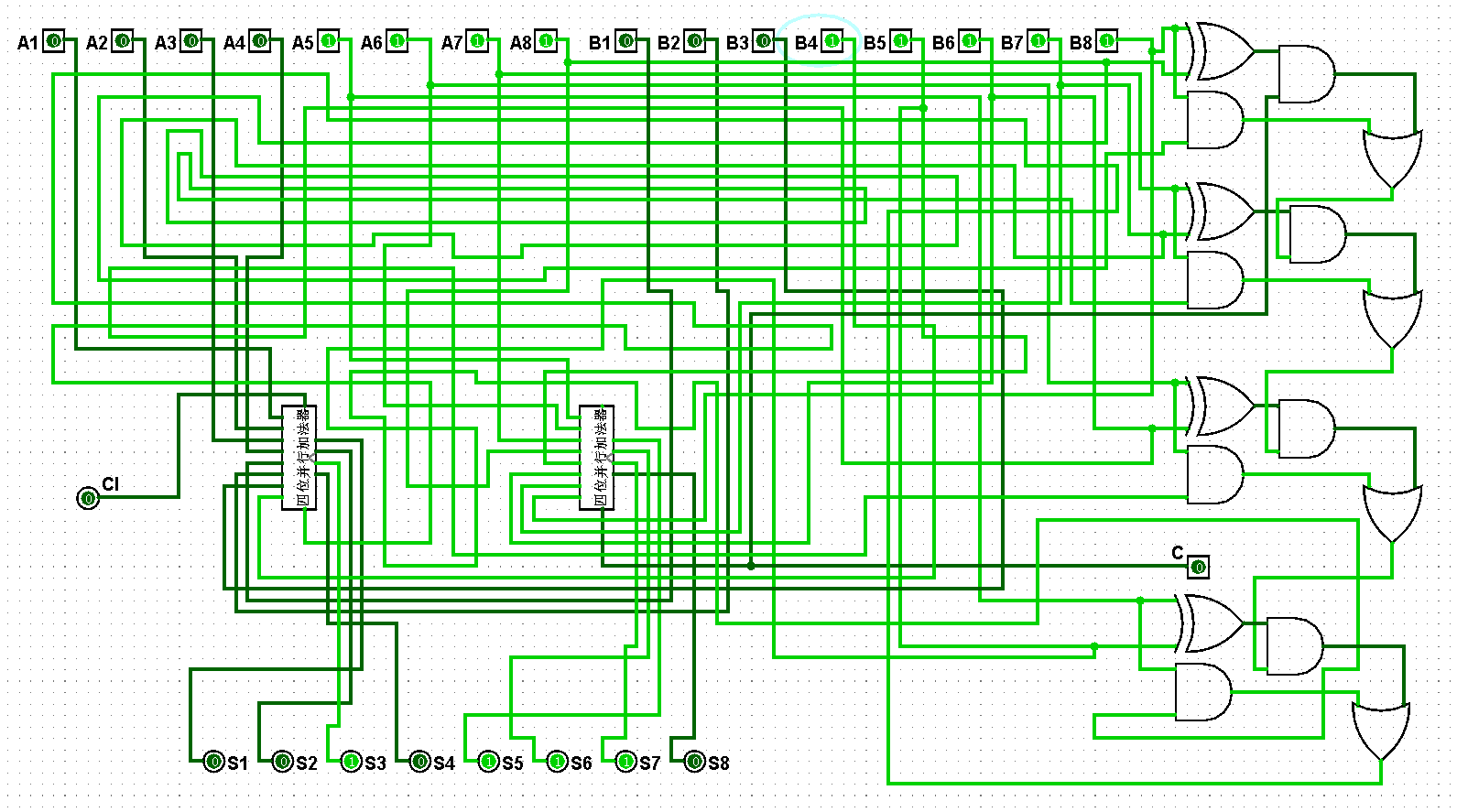
图5-3-11 八位并行加法器测试15+31=46
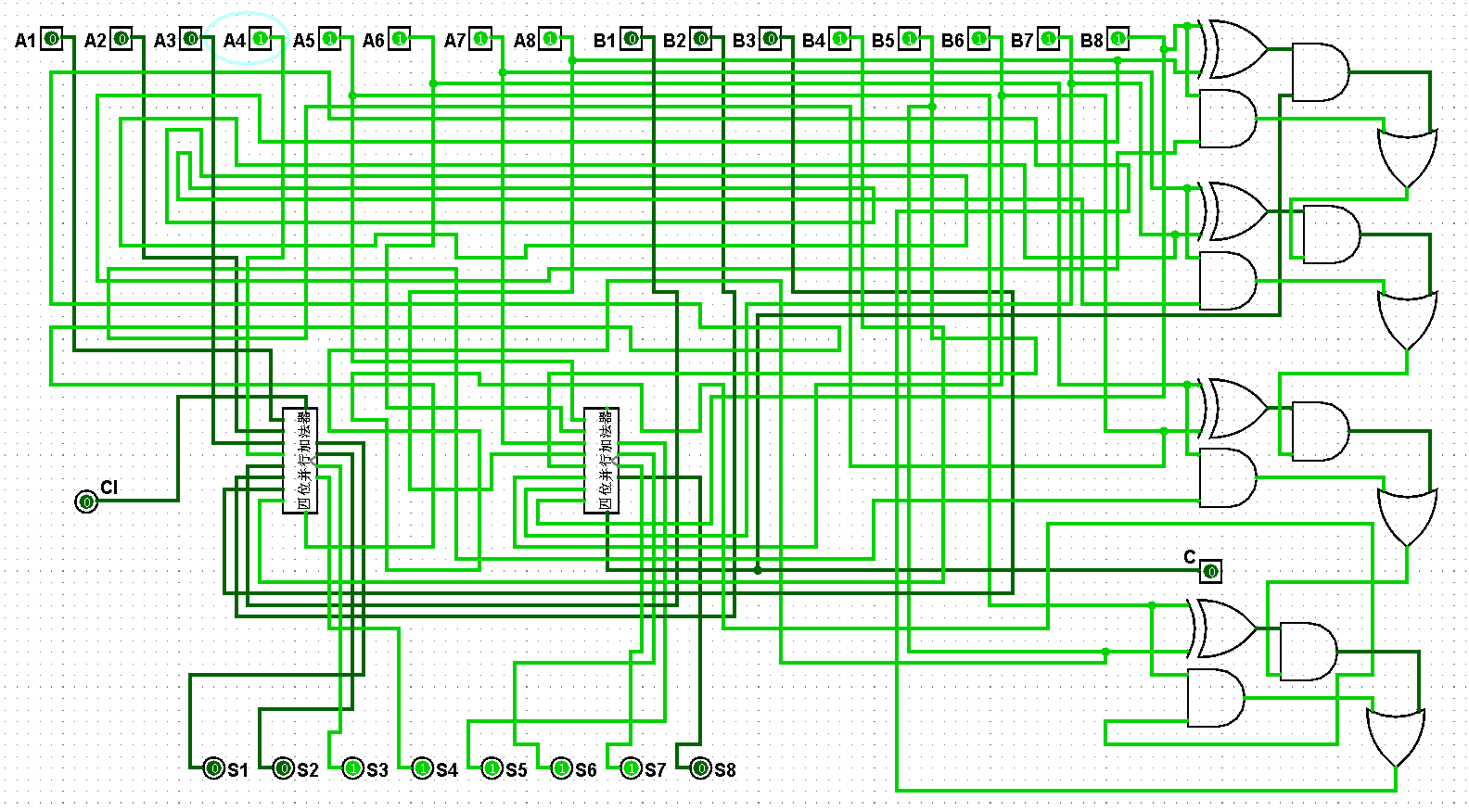
图5-3-12 八位并行加法器测试31+31=62
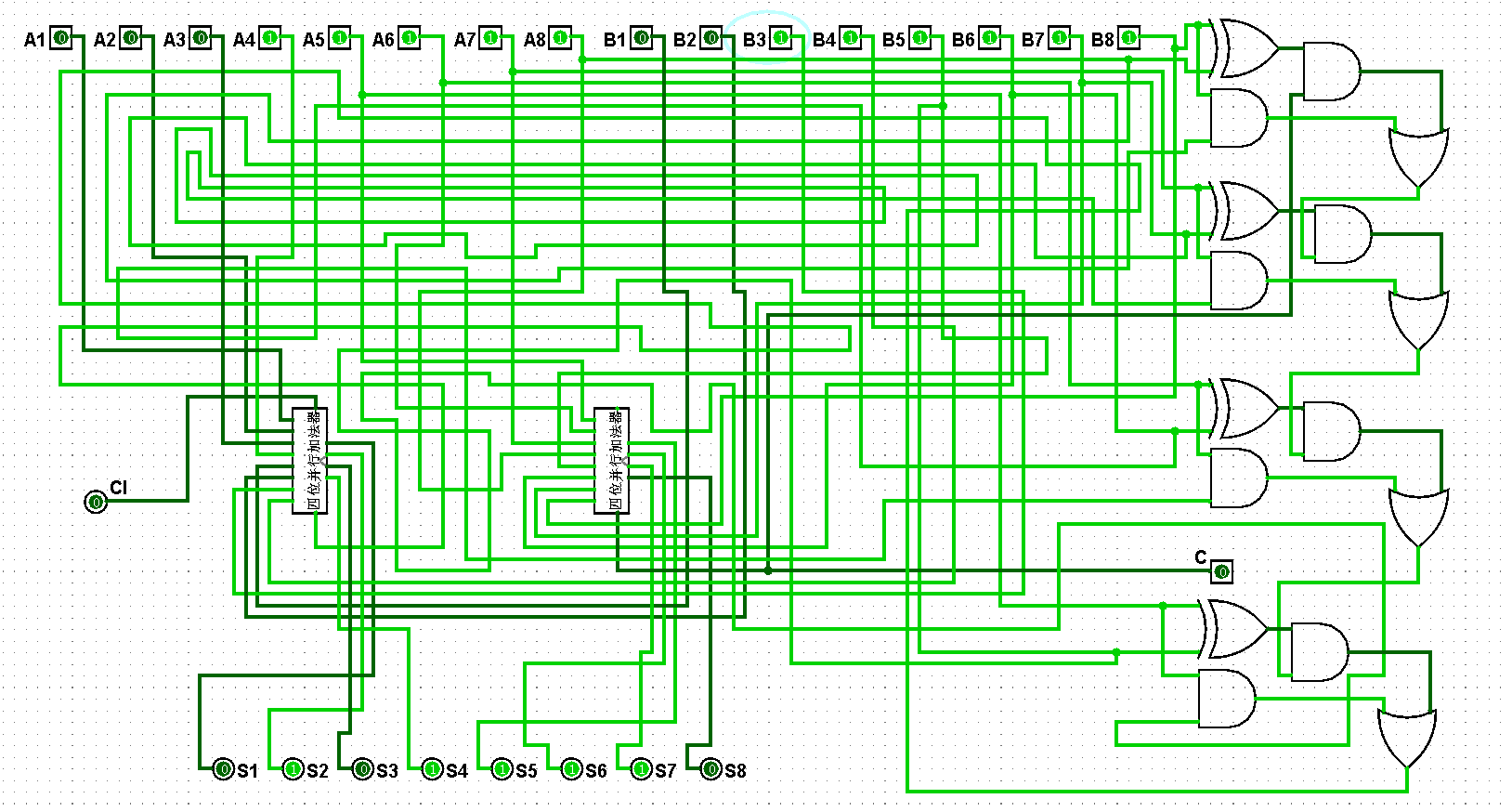
图5-3-13 八位并行加法器测试31+63=94
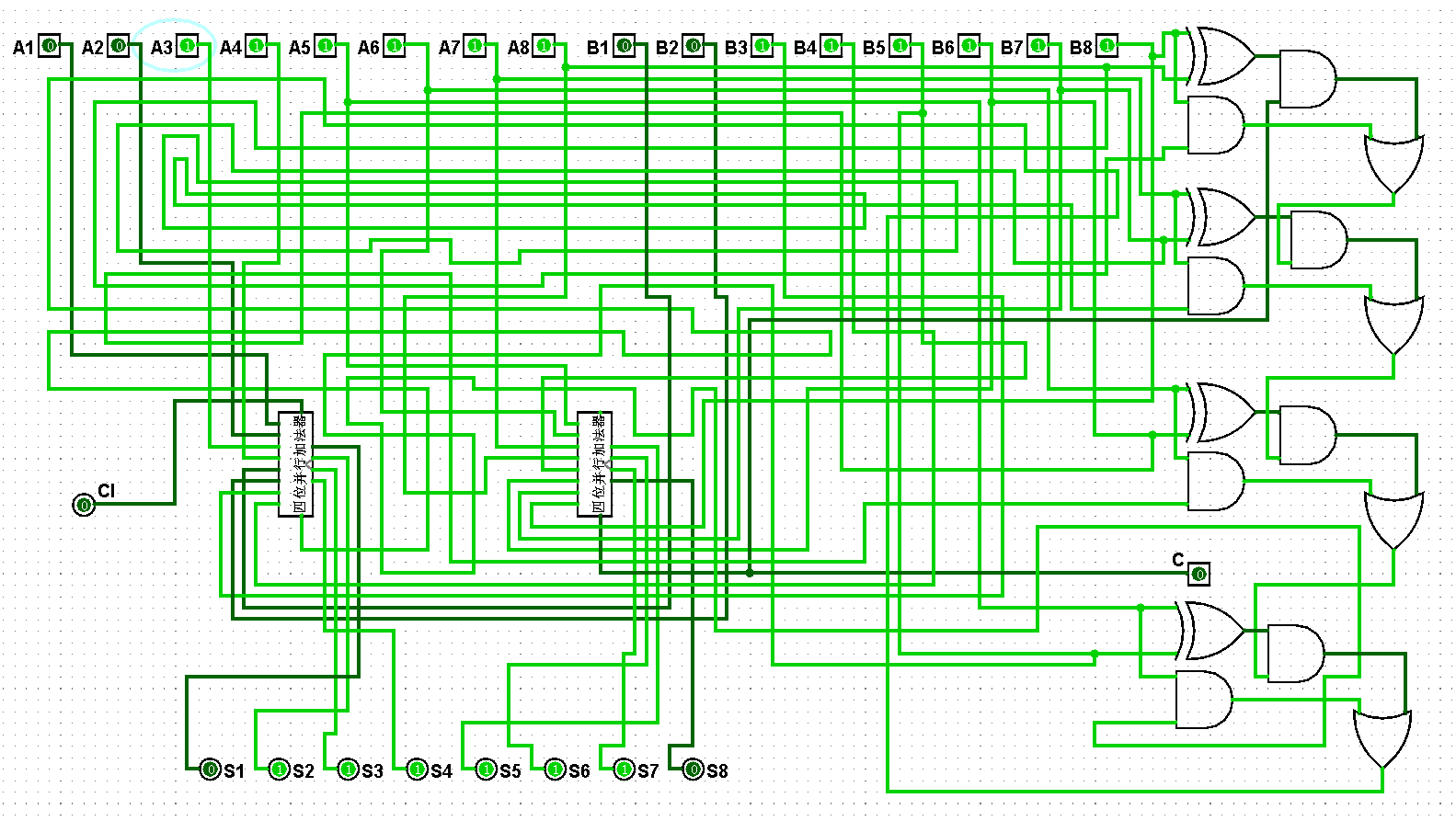
图5-3-14 八位并行加法器测试63+63=126
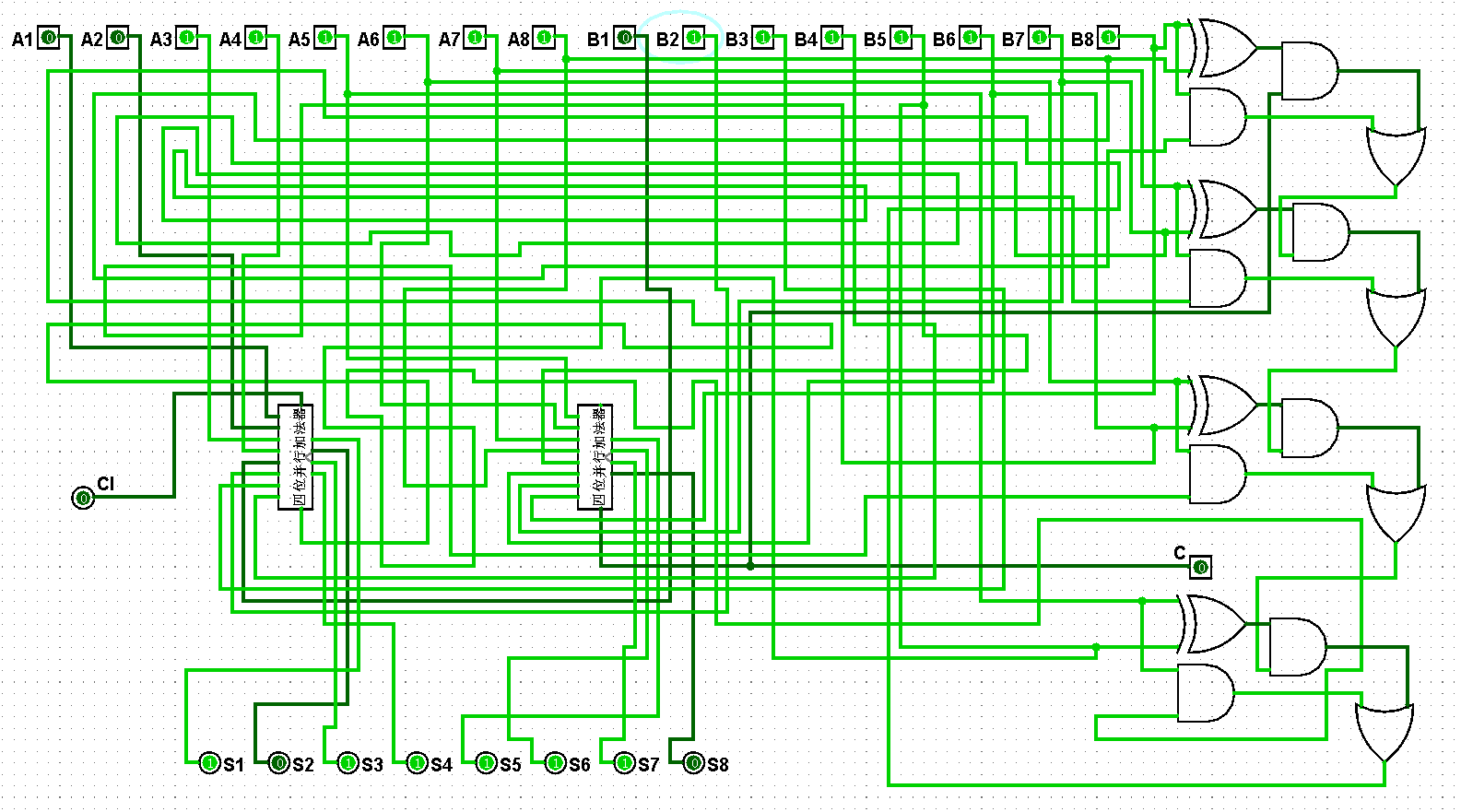
图5-3-15 八位并行加法器测试63+127=190
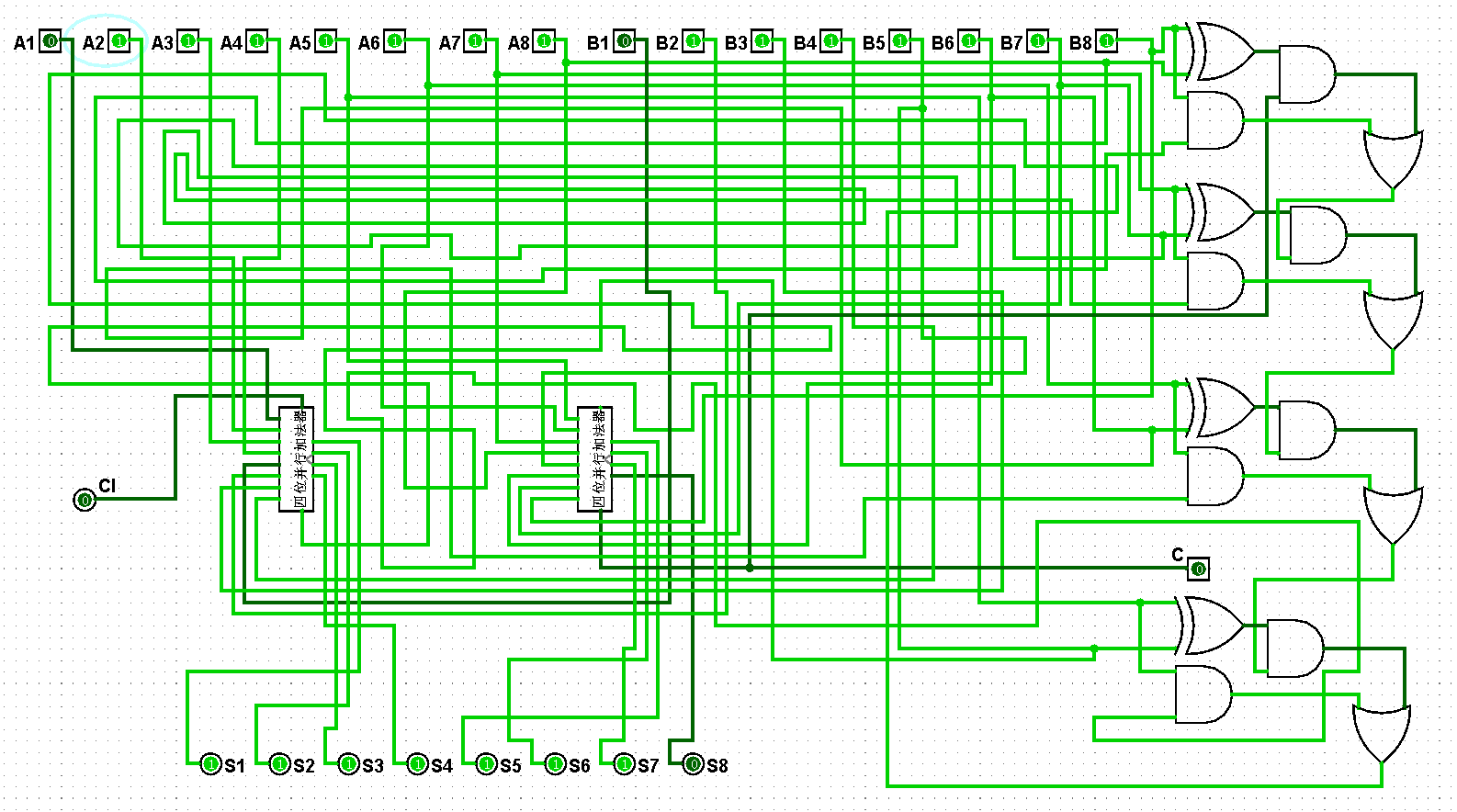
图5-3-16 八位并行加法器测试127+127=254
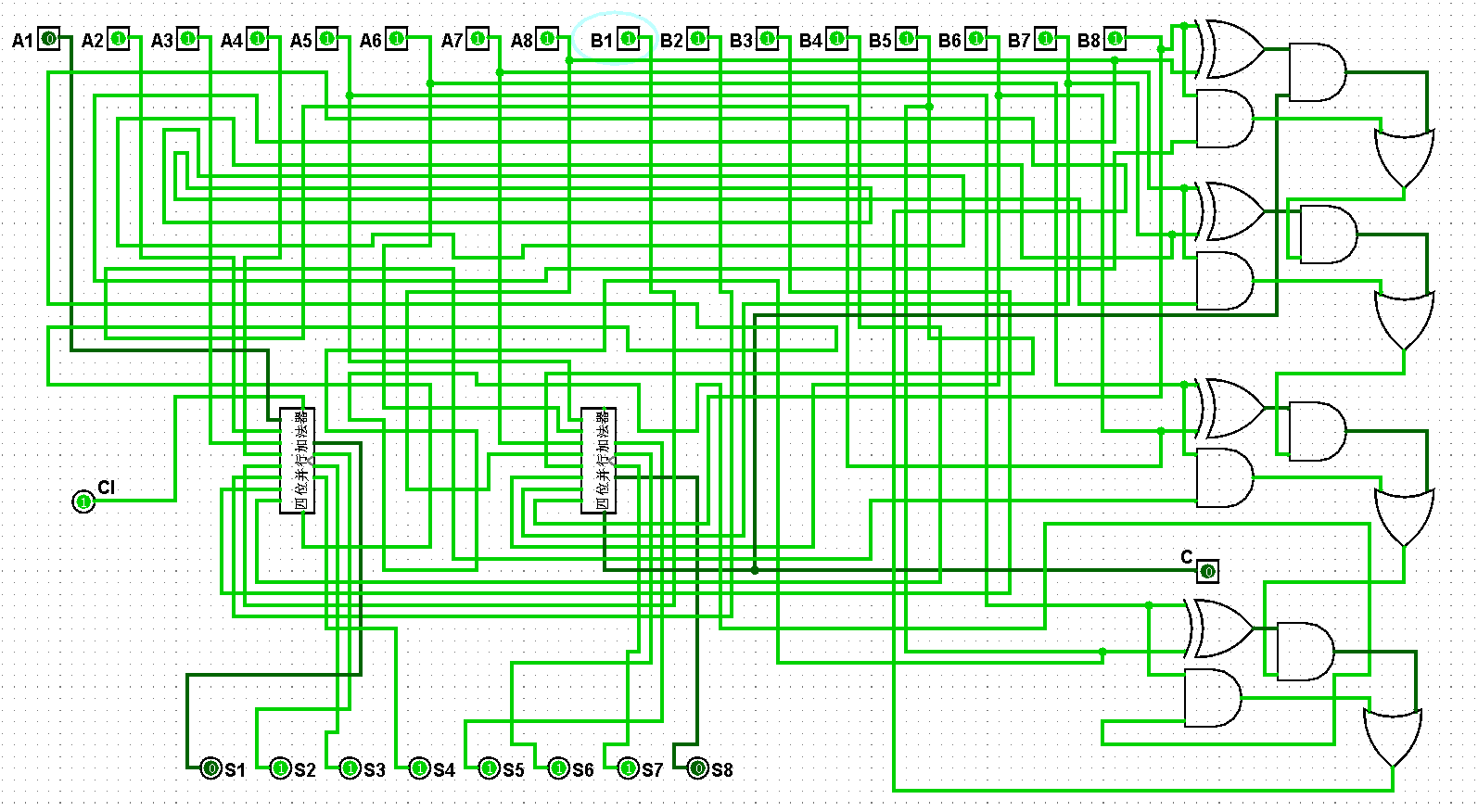
图5-3-17 八位并行加法器测试127+255=382
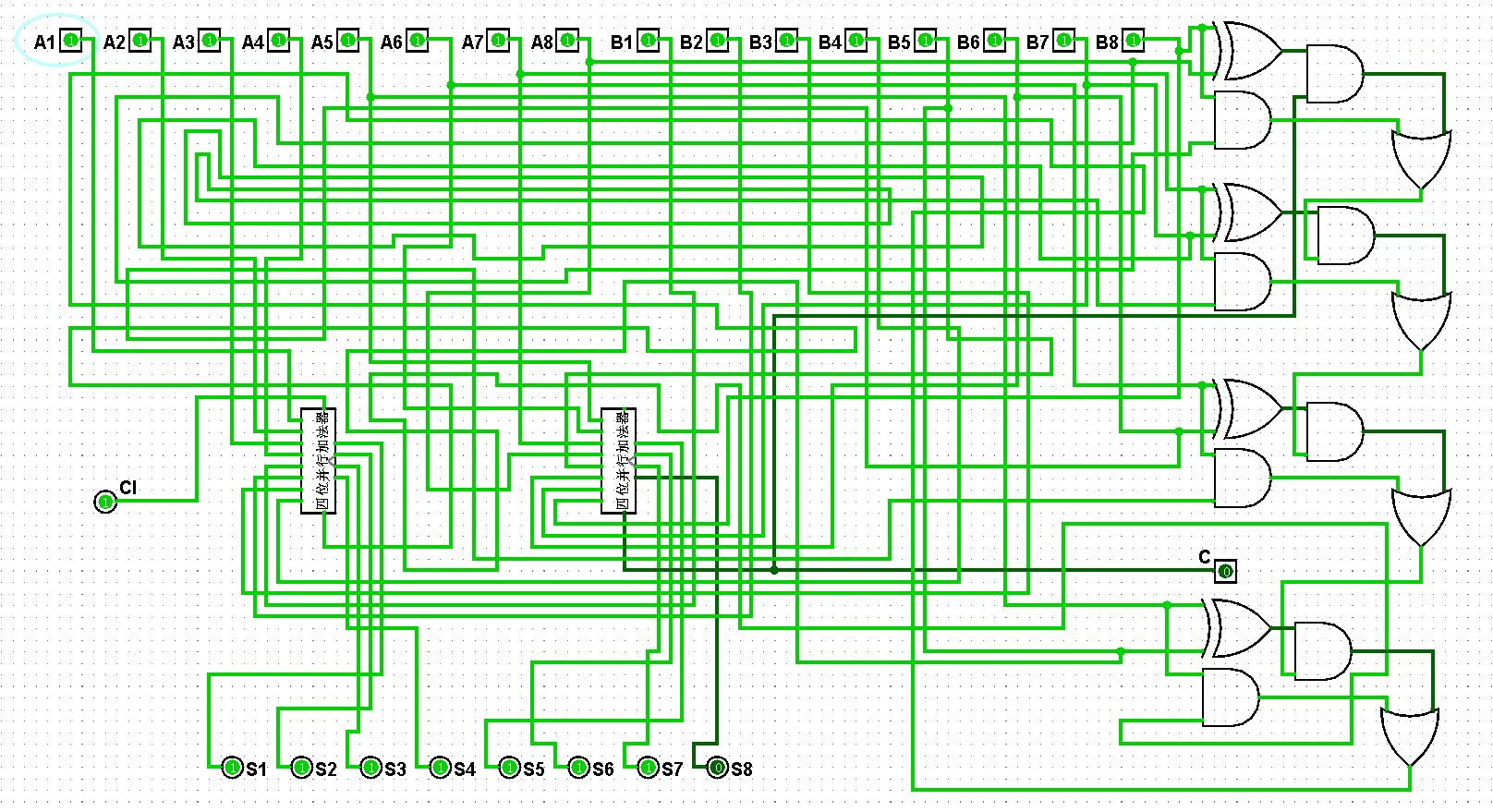
图5-3-18 八位并行加法器测试255+255=510
5、打开Logisim软件,用自己学号(20212501238)最后两位数字(38)转化为二进制(00000011,00001000)作为输入,测试两个八位加法器的功能。
(1)将对应的八位二进制分别输入到八位串行加法器和八位并行加法器中进行运算,对应的八位串行加法器、八位并行加法器逻辑电路真值表分别如图5-5-1、5-5-2所示:

图5-5-1 八位串行加法器逻辑电路真值表

图5-5-2 八位并行加法器逻辑电路真值表
(2)将转化后的八位二进制直接输入到对应的加法器中进行计算输出即可,对应的八位串行加法器、八位并行加法器输入逻辑电路分别如图5-5-3、5-5-4所示:
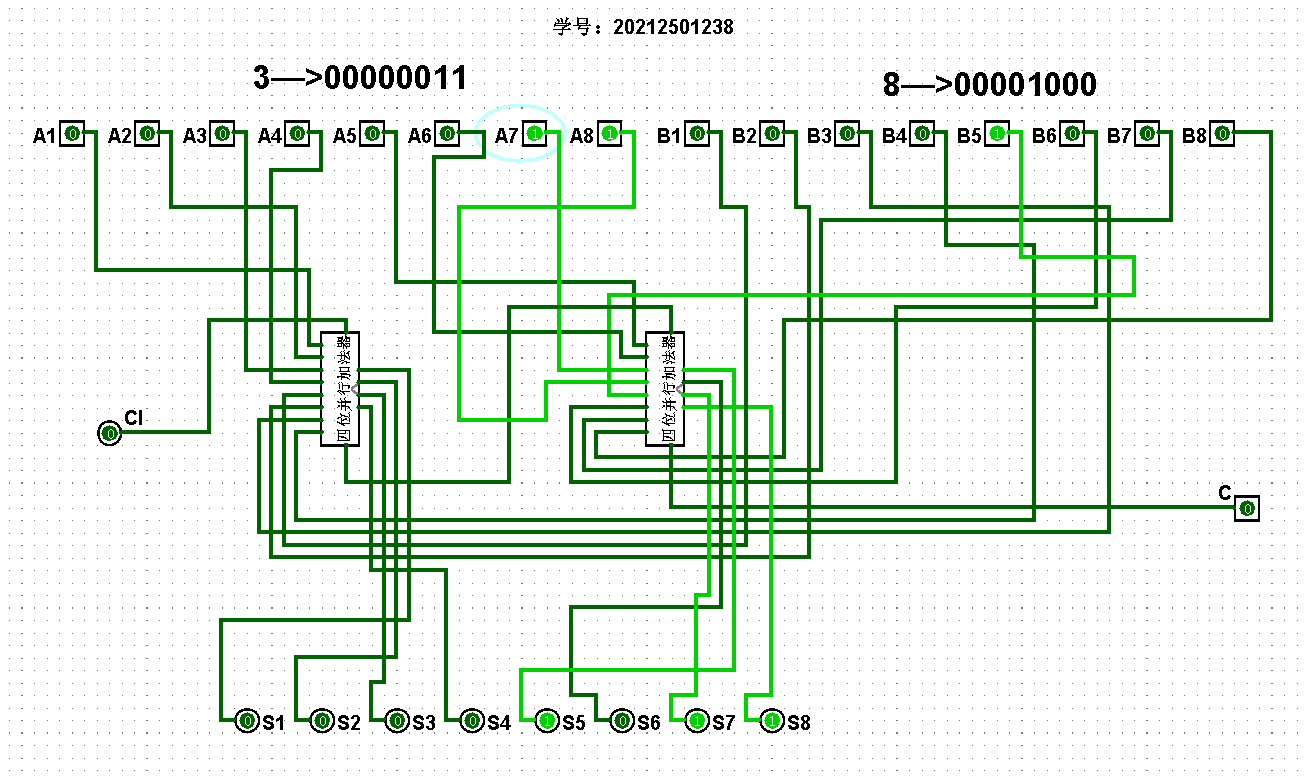
图5-5-3 八位串行加法器输入逻辑电路

图5-5-4 八位并行加法器输入逻辑电路
六、实验小结
1、问题和解决方法:
(1)实验问题:使用逻辑门和相关元素构建逻辑电路后发现有时输出结果与自己的真值表内容不符。
解决方法:观察自己的逻辑电路后发现部分逻辑门的引脚过多,与、或、非等逻辑门的默认引脚的个数为5个,因此我们需要根据自己需要的引脚数量进行设置,将对应的引脚数量改为自己需要的2个引脚后对应问题得到解决。
(2)实验问题:在对逻辑门进行连线的过程中发现电路中出现了多余的连线。
解决方法:点击对应多余的连线并进行删除操作或者对该条连线重新进行勾连。
(3)实验问题:逻辑电路连接完成后发现部分输入端或者输出端是蓝色,且点击输入端进行数值切换对蓝色的输出端无影响。
解决方法:线路没有彻底连接,输入端和输出端的引脚默认朝西,所以在连接电路时要首先将对应端口的引脚方向进行设置,进而方便逻辑电路的正常连接。
(4)实验问题:逻辑电路中有部分区域的连线为红色。
解决方法:由于红色连线前方处于断路状态,逻辑信号无法正常到达后续的逻辑电路之中,因此出现了红色连线,将对应区段的电路连接通路后即可恢复正常。
(5)实验问题:在使用两个以上的异或门进行逻辑电路操作时发现出现了错误。
解决方法:由于Logisim允许指定异或门的逻辑行为,默认是当一个输入为1是输出为1,另一种是奇数个1输入时输出为1,因此在使用过程中需要对默认值进行相应的修改操作,进而避免错误的出现。
(6)实验问题:逻辑电路设计完毕以后,出现了红色或者橘红色的线条,但是自己的逻辑电路没有任何的错误。
解决方法:由于软件本身因素引起的,因此对自己的逻辑电路进行保存,关闭Logisim软件后重新打开对应的逻辑电路文件后即可恢复正常。
2、心得体会:
(1)通过使用Logisim软件对逻辑电路进行操作,让我熟悉了相关的逻辑符号及逻辑运算等。其中蓝色的方框表示输入信号;蓝色的圆框表示输出信号;绿色的圆圈加上短横表示锚,主要用于移动和定位。
(2)逻辑电路是用来对数字信号进行逻辑运算,以实现逻辑命题的电路。
(3)组合逻辑电路中电路的输出只与该时刻的输入有关,而时序逻辑电路中电路的输出不仅与该时刻的输入有关,还与电路的原状态有关。
(4)真值表是描述逻辑功能的最底层工具,它是先结构而后内容的,列数据时输入部分从全0到全1,逐个递增。
(5)基本逻辑运算是与、或、非,而常用的复合逻辑为与非、或非、与或非、异或、同或。
(6)逻辑门电路(门电路)用于实现各种的基本逻辑运算、常用符合逻辑运算的电子电路。
(7)两输入异或、同或互为反函数,即非关系。
(8)两输入异或、同或的功能为:
两输入异或,输入取值不同,输出1,输入取值相同,输出0;
两输入同或,输入取值不同,输出1,输入取值相同,输出0.
(9)n输入异或的功能为当输入中有奇数个1时,输出值为1,有偶数个1时输出值为0.
(10)n为偶数时,异或、同或互为非关系;n为奇数时,异或、同或功能相同。
(11)编码器用于编码,使用二进制代码表示具有某种特定含义的信号,即输入信号输出代码。
(12)译码器用于译码,将使用一组代码表示的特定含义翻译出来,即输入代码输出信号。
(13)进行溢出判断时可以采取以下三种方法进行判断:
①用计算结果的符号位来判断溢出。
②用计算结果最高数值位向符号位的进位值c1与符号位的进位值c0来判断溢出。
③采用双符号位进行判断。
(14)多位加法器的构成有两种方式:并行进位和串行进位方式。
(15)并行进位加法器设有并行进位产生逻辑,运算速度快;串行进位方式是将全加器级联构成多位加法器。
(16)通常,并行加法器比串行级联加法器占用更多的资源,并且随着位数的增加,相同位数的并行加法器比串行加法器的资源占用差距也会越来越大。
(17)多位全加器连接可以是逐位进位,也可以是超前进位。逐位进位也称串行进位,其逻辑电路简单,但速度也较低。
