当前位置：首页 > ops >正文

相机标定相关原理

ops 2025/7/27 16:56:34

相机标定相关原理

相机标定
- - - **一、标定的核心思想**
    - **二、标定流程与原理**
    - - **1. 数据采集**
      - **2. 单应性矩阵估计（Homography）**
      - **3. 内参约束与闭合解**（详细参考 *补充内容2*）
      - **4. 外参计算**
      - **5. 畸变参数估计**
      - **6. 非线性优化（Bundle Adjustment）**
    - **三、标定关键问题**
    - **四、数学工具总结**
  - **总结**
补充内容1：A 矩阵
- - **A 矩阵的定义与作用**
  - **A 矩阵的构造原理**
  - - 1. **单应性投影方程**
    - 2. **消去尺度因子 $s$ **
    - 3. **构造单点约束矩阵**
    - 4. **组装全局矩阵 A**
  - **求解方法**
  - - 1. **齐次方程组求解**
    - 2. **SVD 分解**
    - 3. **恢复单应性矩阵**
  - **示例（1个角点）**
  - **为什么需要 $\geq 4$ ？**
  - **A 矩阵的数学意义**
  - **总结**
补充内容2：内参约束与闭合解
- - - 一、旋转矩阵正交性的物理意义
    - 二、内参约束的推导过程
    - - 1. 从单应性矩阵建立关系
      - 2. 解耦旋转向量
      - 3. 应用正交性约束
    - 三、内参约束的几何解释
    - 四、闭合解的求解原理
    - - 1. 构建线性方程组
      - 2. 矩阵化表示
      - 3. SVD求解
      - 4. 恢复内参矩阵
    - 五、关键点图解
    - 六、数学本质
    - 七、实际应用

相机标定

相机标定的核心目标是确定相机的内部几何特性（内参）和外部空间位置（外参），同时补偿镜头畸变。其数学本质是通过已知的3D-2D点对应关系，求解投影方程中的未知参数。

一、标定的核心思想

输入数据：
- 已知空间位置的3D点（如棋盘格的角点，设其世界坐标为 $X_w, Y_w, Z_w)$ ）
- 这些点在图像中的2D投影坐标 $(u, v)$
数学模型：
$\begin{bmatrix} u \\ v \\ 1 \end{bmatrix} = \underbrace{\begin{bmatrix} f_x & s & u_0 \\ 0 & f_y & v_0 \\ 0 & 0 & 1 \end{bmatrix}}_{\text{内参矩阵 } K} \cdot \underbrace{\begin{bmatrix} r_{11} & r_{12} & r_{13} & t_x \\ r_{21} & r_{22} & r_{23} & t_y \\ r_{31} & r_{32} & r_{33} & t_z \end{bmatrix}}_{\text{外参矩阵 } [R|t]} \begin{bmatrix} X_w \\ Y_w \\ Z_w \\ 1 \end{bmatrix}$
- $s$ ：尺度因子（深度相关）
- 需求解：内参 $K$ （5个自由度）、外参 $R, t$ （6个自由度，分别对应旋转3个(俯仰（pitch）、偏航（yaw）、翻滚（roll))和平移3个(相机在世界坐标系中的 $x, y, z$ 坐标)）、畸变参数

二、标定流程与原理

1. 数据采集

工具：棋盘格标定板（已知方格尺寸）
要求：
- 拍摄15-20张不同姿态的标定板图像
- 覆盖图像边缘/中心、倾斜/正对等场景
检测：使用角点检测算法（如Harris）获取角点的像素坐标 $(u, v)$

2. 单应性矩阵估计（Homography）

定义：单应性矩阵（Homography Matrix）是计算机视觉和图像处理中的一个重要概念，用于描述两个平面之间的投影变换关系。单应性矩阵 $H$ 是一个3×3的矩阵，通过齐次坐标表示点的映射关系：
$[x′y′1]=H⋅[xy1]\begin{bmatrix} x' \\ y' \\ 1 \end{bmatrix} = H \cdot \begin{bmatrix} x \\ y \\ 1 \end{bmatrix}$
其中 (x, y) 是原图像中的点，(x’, y’) 是目标图像中的对应点， H 的形式为：
$\begin{bmatrix} h_{11} & h_{12} & h_{13} \\ h_{21} & h_{22} & h_{23} \\ h_{31} & h_{32} & h_{33} \end{bmatrix}$
由于齐次坐标的尺度不变性， H 实际只有8个自由度（通常设 $h_{33} = 1$ 或约束模长为1）。
张正友标定法：
（1）张正友标定法：核心思想是通过多幅平面标定板图像的对应点，求解相机内参和畸变系数。该方法要求标定板必须是平面，且通过不同姿态的标定板图像（即改变 $Z = 0$ 平面的旋转和平移）来覆盖三维空间的变化，从而间接约束相机参数。
（2）平面约束的数学便利性：棋盘格是一个平面物体，将其定义为 $Z = 0$ 平面后，世界坐标系中的点三维坐标变为 $(X, Y, 0)$ ，从而将三维到二维的投影问题简化为二维平面到图像的映射问题。此时，相机外参中的旋转矩阵 $R$ 和平移向量 $t$ 仅需描述标定板平面与相机坐标系之间的相对关系，无需考虑深度方向的复杂变换。
核心观察：棋盘格平面满足 $Z_w = 0$ ，投影方程简化为：
$\begin{bmatrix} u \\ v \\ 1 \end{bmatrix} = K \begin{bmatrix} r_1 & r_2 & t \end{bmatrix} \begin{bmatrix} X_w \\ Y_w \\ 1 \end{bmatrix} = H \begin{bmatrix} X_w \\ Y_w \\ 1 \end{bmatrix}$
- $H$ 是3×3单应性矩阵（Homography），联系平面世界坐标与像素坐标
求解方法（详细参考 补充内容1）：
- 每张图像提供 $N$ 个点对应（ $\geq 4$ ）
- 构建线性方程组： $A h = 0$ （ $h$ 为 $H$ 的向量形式）
- 通过SVD分解求最小二乘解

3. 内参约束与闭合解（详细参考补充内容2）

旋转矩阵正交性： $r_1^T r_2 = 0$ ， $r_1\| = \|r_2\| = 1$
推导内参约束：
${h1TK−TK−1h2=0h1TK−TK−1h1=h2TK−TK−1h2\begin{cases} h_1^T K^{-T} K^{-1} h_2 = 0 \\ h_1^T K^{-T} K^{-1} h_1 = h_2^T K^{-T} K^{-1} h_2 \end{cases}$
其中 $h_1, h_2$ 是 $H$ 的前两列
求解内参：
- 定义对称矩阵 $B = K^{-T} K^{-1}$
- 多张图像构建超定方程组 $Vb = 0$ （ $b$ 为 $B$ 的向量形式）
- 通过SVD求解 $B$ ，再经Cholesky分解得 $K$

4. 外参计算

由单应性矩阵 $H$ 和内参 $K$ 计算外参：
$r1=λK−1h1r2=λK−1h2r3=r1×r2t=λK−1h3\begin{align*} r_1 &= \lambda K^{-1} h_1 \\ r_2 &= \lambda K^{-1} h_2 \\ r_3 &= r_1 \times r_2 \\ t &= \lambda K^{-1} h_3 \end{align*}$
（ $λ=1/∥K−1h1∥\lambda = 1 / \|K^{-1}h_1\|$ 为归一化因子）

5. 畸变参数估计

畸变模型（修正归一化坐标）：
${xcorr=x(1+k1r2+k2r4)+2p1xy+p2(r2+2x2)ycorr=y(1+k1r2+k2r4)+p1(r2+2y2)+2p2xy\begin{cases} x_{\text{corr}} = x (1 + k_1 r^2 + k_2 r^4) + 2p_1 xy + p_2 (r^2 + 2x^2) \\ y_{\text{corr}} = y (1 + k_1 r^2 + k_2 r^4) + p_1 (r^2 + 2y^2) + 2p_2 xy \end{cases}$
- $r^2 = x^2 + y^2$ ， $(x, y)$ 为归一化坐标
- $k_1, k_2$ ：径向畸变系数， $p_1, p_2$ ：切向畸变系数
求解：将畸变模型代入投影方程，构建非线性最小二乘问题

6. 非线性优化（Bundle Adjustment）

目标函数：最小化重投影误差（Reprojection Error）
$min⁡θ∑i=1M∑j=1N∥pij−p^(θ,Pj)∥2\min_{\theta} \sum_{i=1}^{M} \sum_{j=1}^{N} \| \mathbf{p}_{ij} - \hat{\mathbf{p}}(\theta, \mathbf{P}_j) \|^2$
- $θ\theta$ ：所有参数（内参+外参+畸变）
- $pij\mathbf{p}_{ij}$ ：第 $j$ 个点在图像 $i$ 中的实测像素坐标
- $p^\hat{\mathbf{p}}$ ：通过投影模型计算的预测像素坐标
优化方法：
- Levenberg-Marquardt算法
- 利用初始解（闭合解）迭代优化至收敛

三、标定关键问题

为什么需要多张图像？
- 单张图像提供8个约束（每个点2个方程），但内参有5自由度+外参6自由度。
- 多张图像增加约束，避免解的不确定性。
为什么棋盘格有效？
- 角点坐标精确已知（ $Z_w=0$ 简化计算）
- 高对比度角点易检测，抗噪声能力强
重投影误差的意义：
- 标定精度的核心指标（单位：像素）
- 理想值：< 0.5像素（工业级应用要求更高）

四、数学工具总结

步骤	数学方法	输出
单应性矩阵估计	线性最小二乘（SVD）	$H3×3H_{3\times3}$
内参闭合解	正交约束+Cholesky分解	$K$
外参计算	矩阵分解	$R, t$
畸变与全局优化	非线性最小二乘（LM算法）	所有参数+畸变系数

总结

相机标定是通过几何约束（旋转矩阵正交性）和优化技术（最小化重投影误差）求解相机参数的过程：

利用平面标定板简化投影模型（单应性矩阵）
通过正交约束解耦内参/外参
非线性优化联合 refine 所有参数
畸变模型补偿镜头非线性误差

标定结果直接影响后续的三维重建、立体视觉、SLAM等任务的精度，是计算机视觉系统的基石。

补充内容1：A 矩阵

在单应性矩阵估计中，矩阵 A 是一个关键的设计矩阵（Design Matrix），它由所有观测点对的约束方程构建而成。以下是详细解释：

A 矩阵的定义与作用

A 是一个 $2n \times 9$ 的矩阵（ $n$ 是角点数量），用于求解单应性矩阵 $H$ 的向量化形式 $h\mathbf{h}$ 。其核心是将非线性投影关系转化为线性齐次方程组：
$\mathbf{h} = 0$
其中：

$h\mathbf{h}$ 是单应性矩阵 $H$ 的向量化形式： $h=[h11,h12,h13,h21,h22,h23,h31,h32,h33]T\mathbf{h} = [h_{11}, h_{12}, h_{13}, h_{21}, h_{22}, h_{23}, h_{31}, h_{32}, h_{33}]^T$
A 的每一行对应一个角点产生的约束方程

A 矩阵的构造原理

1. 单应性投影方程

对于世界坐标系中的点 $X_w, Y_w, 0)$ （棋盘格平面 $Z_w = 0$ ) 和其像素坐标 $(u, v)$ ，有：
$\begin{bmatrix} u \\ v \\ 1 \end{bmatrix} = H \begin{bmatrix} X_w \\ Y_w \\ 1 \end{bmatrix}, \quad H = \begin{bmatrix} h_{11} & h_{12} & h_{13} \\ h_{21} & h_{22} & h_{23} \\ h_{31} & h_{32} & h_{33} \end{bmatrix}$

2. 消去尺度因子 $s$

展开方程并消去 $s$ ：
${u=h11Xw+h12Yw+h13h31Xw+h32Yw+h33v=h21Xw+h22Yw+h23h31Xw+h32Yw+h33\begin{cases} u = \frac{h_{11} X_w + h_{12} Y_w + h_{13}}{h_{31} X_w + h_{32} Y_w + h_{33}} \\ v = \frac{h_{21} X_w + h_{22} Y_w + h_{23}}{h_{31} X_w + h_{32} Y_w + h_{33}} \end{cases}$
整理为线性形式：
${h11Xw+h12Yw+h13−u(h31Xw+h32Yw+h33)=0h21Xw+h22Yw+h23−v(h31Xw+h32Yw+h33)=0\begin{cases} h_{11} X_w + h_{12} Y_w + h_{13} - u (h_{31} X_w + h_{32} Y_w + h_{33}) = 0 \\ h_{21} X_w + h_{22} Y_w + h_{23} - v (h_{31} X_w + h_{32} Y_w + h_{33}) = 0 \end{cases}$

3. 构造单点约束矩阵

对每个角点 $(Xw,Yw)→(u,v)(X_w, Y_w) \rightarrow (u, v)$ ，生成两行约束：
$Ai=[XwYw1000−uXw−uYw−u000XwYw1−vXw−vYw−v]A_i = \begin{bmatrix} X_w & Y_w & 1 & 0 & 0 & 0 & -u X_w & -u Y_w & -u \\ 0 & 0 & 0 & X_w & Y_w & 1 & -v X_w & -v Y_w & -v \end{bmatrix}$

4. 组装全局矩阵 A

将所有 $n$ 个角点的约束堆叠：
$\begin{bmatrix} A_1 \\ A_2 \\ \vdots \\ A_n \end{bmatrix}_{2n \times 9}$

求解方法

1. 齐次方程组求解

问题转化为：
$min⁡h∥Ah∥2s.t.∥h∥=1\min_{\mathbf{h}} \| A \mathbf{h} \|^2 \quad \text{s.t.} \quad \| \mathbf{h} \| = 1$
（约束 $∥h∥=1\|\mathbf{h}\|=1$ 避免零解）

2. SVD 分解

对 $A$ 进行奇异值分解（SVD）：
$\Sigma V^T$
解 $h\mathbf{h}$ 是 $V$ 的最后一列（最小奇异值对应的右奇异向量）。

3. 恢复单应性矩阵

$h\mathbf{h}$ 重构为 $H$ ：
$\begin{bmatrix} h_{11} & h_{12} & h_{13} \\ h_{21} & h_{22} & h_{23} \\ h_{31} & h_{32} & h_{33} \end{bmatrix}$

示例（1个角点）

假设角点世界坐标 $X_w, Y_w) = (2, 3)$ ，像素坐标 $(u, v) = (100, 200)$ ，则其约束矩阵为：
$Ai=[231000−100×2−100×3−100000231−200×2−200×3−200]=[231000−200−300−100000231−400−600−200]A_i = \begin{bmatrix} 2 & 3 & 1 & 0 & 0 & 0 & -100 \times 2 & -100 \times 3 & -100 \\ 0 & 0 & 0 & 2 & 3 & 1 & -200 \times 2 & -200 \times 3 & -200 \end{bmatrix} = \begin{bmatrix} 2 & 3 & 1 & 0 & 0 & 0 & -200 & -300 & -100 \\ 0 & 0 & 0 & 2 & 3 & 1 & -400 & -600 & -200 \end{bmatrix}$

为什么需要 $\geq 4$ ？

单应性矩阵 $H$ 有 8 个自由度（尺度不变性）。
每个角点提供 2 个独立方程。
需满足 $\geq 8$ ⇒ $\geq 4$ 才能得到唯一解。

A 矩阵的数学意义

线性化工具：将非线性投影转换为线性约束。
超定系统基础：当 $n > 4$ 时， $A$ 是超定矩阵，通过 SVD 求最小二乘解。
解的空间：零空间（Null Space）的基向量对应可能的 $h\mathbf{h}$ ，SVD 选取最优基。

总结

矩阵 A 是单应性估计的核心构造：

结构： $2n \times 9$ 的系数矩阵（ $n$ 为角点数）。
元素来源：每个角点根据其 $X_w, Y_w)$ 和 $(u, v)$ 生成两行约束。
求解目标：最小化 $∥Ah∥\| A \mathbf{h} \|$ 得到 $H$ 的最优解。
实际应用：在 OpenCV 的 findHomography() 或 calibrateCamera() 的第一步中隐式构建并求解。

补充内容2：内参约束与闭合解

一、旋转矩阵正交性的物理意义

在相机标定中，外参矩阵的旋转部分 $R$ 是正交矩阵，具有两个核心性质：

列向量正交性： $r_1^T r_2 = 0$
（相机坐标系的X轴与Y轴垂直）
单位长度性： $r_1^T r_1 = r_2^T r_2$
（相机坐标系各轴均为单位向量）

这些性质源于三维空间的刚体运动特性：

相机安装时，其感光元件的X/Y轴严格垂直
旋转矩阵必须保持坐标系基向量的长度不变
数学表达： $R^T R = I$ （正交矩阵定义）

二、内参约束的推导过程

关键步骤是将旋转约束转换为关于内参的约束：

1. 从单应性矩阵建立关系

已知单应性矩阵 $H$ 与内外参的关系：
$\lambda K \begin{bmatrix} r_1 & r_2 & t \end{bmatrix}$
其中 $λ\lambda$ 为尺度因子。提取前两列：
${h1=λKr1h2=λKr2\begin{cases} h_1 = \lambda K r_1 \\ h_2 = \lambda K r_2 \end{cases}$

2. 解耦旋转向量

反解 $r_1$ 和 $r_2$ ：
${r1=1λK−1h1r2=1λK−1h2\begin{cases} r_1 = \frac{1}{\lambda} K^{-1} h_1 \\ r_2 = \frac{1}{\lambda} K^{-1} h_2 \end{cases}$

3. 应用正交性约束

将 $r_1, r_2$ 代入正交条件：

(1) 正交性约束 $r_1^T r_2 = 0$ 。

(2) 单位长度约束 $r_1^T r_1 = r_2^T r_2$ ：
$(1λK−1h1)T(1λK−1h1)=(1λK−1h2)T(1λK−1h2)h1TK−TK−1h1=h2TK−TK−1h2⇒h1TK−TK−1h1=h2TK−TK−1h2\begin{align*} \left( \frac{1}{\lambda} K^{-1} h_1 \right)^T \left( \frac{1}{\lambda} K^{-1} h_1 \right) &= \left( \frac{1}{\lambda} K^{-1} h_2 \right)^T \left( \frac{1}{\lambda} K^{-1} h_2 \right) \\ h_1^T K^{-T} K^{-1} h_1 &= h_2^T K^{-T} K^{-1} h_2 \\ \Rightarrow \boxed{h_1^T K^{-T} K^{-1} h_1 = h_2^T K^{-T} K^{-1} h_2} \end{align*}$

三、内参约束的几何解释

定义内参关联矩阵：
$K^{-T} K^{-1} = \begin{bmatrix} B_{11} & B_{12} & B_{13} \\ B_{12} & B_{22} & B_{23} \\ B_{13} & B_{23} & B_{33} \end{bmatrix}$
（对称矩阵，6个独立未知量）

则约束转化为：

$h_1^T B h_2 = 0$
$h_1^T B h_1 = h_2^T B h_2$

物理意义：

这些约束建立了图像点坐标（ $h_1, h_2$ 来自单应性矩阵）与相机内部参数（隐藏在 $B$ 中）的直接联系，通过多张图像可构建方程组求解 $B$ 。

四、闭合解的求解原理

1. 构建线性方程组

对每张标定板图像（ $i = 1, 2, ..., m$ ）：

计算单应性矩阵 $H^{(i)}$
提取 $h_1^{(i)}, h_2^{(i)}$
生成两个方程：
${vec(h1(i)h2(i)T)T⋅vec(B)=0vec(h1(i)h1(i)T−h2(i)h2(i)T)T⋅vec(B)=0\begin{cases} \text{vec}(h_1^{(i)} h_2^{(i)T})^T \cdot \text{vec}(B) = 0 \\ \text{vec}(h_1^{(i)} h_1^{(i)T} - h_2^{(i)} h_2^{(i)T})^T \cdot \text{vec}(B) = 0 \end{cases}$

2. 矩阵化表示

组装 $2m \times 6$ 矩阵 $V$ ：
$\begin{bmatrix} v_{1}^{(1)T} \\ v_{2}^{(1)T} \\ \vdots \\ v_{1}^{(m)T} \\ v_{2}^{(m)T} \end{bmatrix}, \quad \text{其中 } \begin{cases} v_1^{(i)} = \text{vec}(h_1^{(i)} h_2^{(i)T}) \\ v_2^{(i)} = \text{vec}(h_1^{(i)} h_1^{(i)T} - h_2^{(i)} h_2^{(i)T}) \end{cases}$
求解：
$\mathbf{b} = 0, \quad \mathbf{b} = [B_{11}, B_{12}, B_{22}, B_{13}, B_{23}, B_{33}]^T$

3. SVD求解

对 $V$ 进行SVD分解： $\Sigma W^T$
解 $b\mathbf{b}$ 是 $W$ 的最后一列（最小奇异值对应的右奇异向量）

4. 恢复内参矩阵

由 $B = K^{-T} K^{-1}$ 通过Cholesky分解：
$K−1=chol(B),K=(K−1)−1K^{-1} = \text{chol}(B), \quad K = (K^{-1})^{-1}$

五、关键点图解

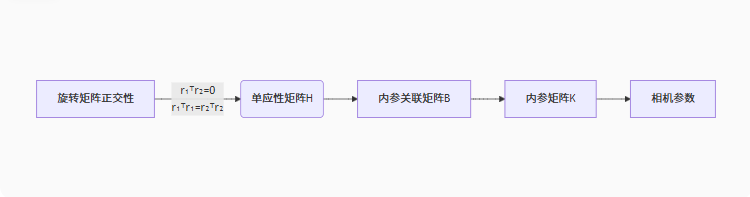
在这里插入图片描述

graph LR
A[旋转矩阵正交性] -->|r₁ᵀr₂=0<br>r₁ᵀr₁=r₂ᵀr₂| B(单应性矩阵H)
B --> C[内参关联矩阵B]
C --> D[内参矩阵K]
D --> E[相机参数]

六、数学本质

该过程的核心是利用旋转矩阵的固有约束（正交性），将不可直接观测的内参与可测量的图像对应点（通过单应性矩阵 $H$ ）联系起来：

自由度分析：
- $B$ 有6个自由度
- 每张图像提供2个约束
- 至少需3张图像求解（ $\times 3 = 6$ ）
闭合解优势：避免非线性优化，直接得到解析解

七、实际应用

在OpenCV的calibrateCamera()中：

# 伪代码流程
homographies = [findHomography(points2D, board3D) for img in images]
V = build_constraint_matrix(homographies)  # 构建约束矩阵
_, _, Vt = cv2.SVDecomp(V)
b = Vt[-1, :]  # 取最后一列
K = compute_K_from_b(b)  # 闭合解计算内参